德杰尼斯五后問題求解方法

李 盤 林，　趙 銘 偉，　徐 喜 榮，　李 麗 雙，　李 伯 章

( 1.大連理工大學 電子信息與電氣工程學部, 遼寧 大連　116024；2. 滑鐵盧大學 計算機工程系， 加拿大 安大略　滑鐵盧 )

?

德杰尼斯五后問題求解方法

李 盤 林*1，趙 銘 偉1，徐 喜 榮1，李 麗 雙1，李 伯 章2

( 1.大連理工大學 電子信息與電氣工程學部, 遼寧 大連116024；2. 滑鐵盧大學 計算機工程系， 加拿大 安大略滑鐵盧 )

摘要：給出了棋盤坐標表示，定義了皇后控制數或剩余控制數，以及皇后最佳(極佳)或剩余最佳(極佳)位置的概念．利用棋盤對稱性，通過有效的計算，先求出了五后問題的3個基礎解，進而得到了全部24個解及其圖示，并首次給出了最少放置5個而不是4個皇后的證明，以及解的完備性證明．

關鍵詞：五后問題；皇后控制數或剩余控制數；皇后最佳(極佳)或剩余最佳(極佳)位置

0引言

在信息領域，八后問題、五后問題，了解它們的不乏其人．前者由高斯解決[1]，后者就不那么幸運了．都說五后問題但其內涵是不同的(http://cjc.iteye.com/blog/299173；http://wenku.baidu.com/view/c254e769a98271fe910ef965.html)．1862年，德杰尼斯[2](De Jaenisch)研究在8×8棋盤上最少放置幾個皇后，它們彼此互不攻擊，又能控制其他任意棋子．他給出7個皇后的解，而正確解是5個．為了不忘德杰尼斯的先期工作，將下面論題：在8×8棋盤上最少放置5個皇后，能否使5個皇后各自安全且又能吃掉棋盤上其余任意棋子(皇后占用的五格不同行、或不同列、或不同一對角線，且又能與棋盤上其余格同行、或同列、或同一對角線)稱為德杰尼斯五后問題[3]．本文給出上述論題的一種解法．

1求解前的說明

(1)8×8棋盤坐標表示，即對由64個稱為格的小正方形構成一個大正方形稱為棋盤的給出坐標表示．大正方形的左下頂點為坐標原點O；大正方形的底邊為坐標x軸；大正方形的左邊為坐標y軸．小正方形的邊長為坐標軸的1個單位；小正方形即格S的右上頂點坐標(i，j)作為S的標記，記為Si,j，簡記為Sij．記(0，0)與(8，8)的連線為cc；記(0，8)與(8，0)的連線為dd；記(0，4)與(8，4)的連線為aa；記(4，0)與(4，8)的連線為bb．稱(4，4)為棋盤的中心點．aa與bb將棋盤劃分為4個區域R1、R2、R3和R4．上述說明如圖1所示．

(2)第1個皇后Q放在格Sij上，位于與Sij同行、同列和同一對角線上的所有格數，稱為皇后Q控制數[4]，記為n(Q|Sij)．使控制數最大的皇后Q所在格Si0j0是唯一的，稱Si0j0為皇后Q最佳位置[4]，記為Qi0j0，其控制數記為n(Qi0j0)；若不唯一，比如說Si1j1，Si2j2，…，稱這些格為皇后Q極佳位置，記為Qi1j1，Qi2j2，…；其控制數分別記為n(Qi1j1)，n(Qi2j2)，…．

類似地可定義第3個、第4個、…皇后剩余控制數、最佳(極佳)位置．

圖1　棋盤定義

2求解及證明

利用棋盤對稱性，欲求第1個皇后A最佳(極佳)位置，只需在區域R1內計算位于cc上及其下面每個格的控制數，并求出最大者即可．經過計算，可知皇后A最佳位置是格S44，皇后A最佳位置記為A44，n(A44)=28．

第2個皇后B剩余最佳(極佳)位置，除去與A44同行、同列和同一對角線所有格外，計算每個格的控制數且給出其最大者即可確定．經過計算，共得到6個皇后B極佳位置：S63、S65、S56、S36、S67和S76，分別記為B63、B65、B56、B36、B67和B76，其剩余控制數分別為n(B63)=16，n(B65)=16，n(B56)=16，n(B36)=16，n(B67)=16和n(B76)=16．

在確定A44、B63后，不難求出：

第3個皇后C剩余最佳位置是格S56，皇后C最佳位置記為C56，其剩余控制數是n(C56)=10．

第4個皇后D剩余最佳位置是格S37，皇后D最佳位置記為D37，其剩余控制數是n(D37)=7．

第5個皇后E剩余最佳位置是格S25，皇后E最佳位置記為E25，其剩余控制數是n(E25)=3．

不難看出，4個皇后是不能夠控制棋盤的，因為

n(A44)+n(B63)+n(C56)+n(D37)=

28+16+10+7=61

這表明還有3個格不被上述4個皇后所控制．放置第5個皇后E后，得到了皇后E剩余最佳位置E25，n(E25)=3；于是

n(A44)+n(B63)+n(C56)+n(D37)+n(E25)=64

整個棋盤才完全被5個皇后所控制．

至此，得到了五后問題的第一個基礎解，表示為A44B63C56D37E25，并證明了在8×8棋盤上最少放置5個皇后才能使5個皇后各自安全且又能吃掉棋盤上其余任意棋子．

類似地可求出五后問題的第二個基礎解為A44B65C36D23E52，其中n(A44)=28，n(B65)=16，n(C36)=10，n(D23)=6，n(E52)=4以及第3個基礎解為A44B56C37D18E25，其中n(A44)=28，n(B56)=16，n(C37)=9，n(D18)=6，n(E25)=5.

對于A44、B67或A44、B76和隨其后所確定的3個剩余最佳位置，均不為所求解．而由A44、B36和隨其后所確定的3個剩余最佳位置所得到的解與由A44、B65所確定的解相同．

將上面3個基礎解，分別以cc、dd、aa、bb多次對折，或多次的對折和以棋盤中心點順時針旋轉90°，便可得到24個解及其圖示，如圖2～9所示．

最后需要指出的是解的完備性問題．在求解過程中，除因利用棋盤對稱性才在局域內求得皇后A最佳位置，其余都是在全域內求得各皇后全部剩余最佳(極佳)位置，并對這些最佳(極佳)位置中的每一個，都分別地完成其求解全過程，直至確定它是解或不是解，可見所求解是完備的．

87654321 (8,8)D37C56E25A44B6312345678(a)解1:A44B63C56D37E2587654321 (8,8)E47D26A55C34B6312345678(b)解2:A55B63C34D26E4787654321 (8,8)D67C46E75A54B3312345678(c)解3:A54B33C46D67E75

圖2　解1～3

87654321 (8,8)E57D76A45C64B3312345678(a)解4:A45B33C64D76E5787654321 (8,8)B36C65A44D73E5212345678(b)解5:A44B36C65D73E5287654321 (8,8)B36A55E74C43D6212345678(c)解6:A55B36C43D62E74

圖3　解4～6

87654321 (8,8)B66A45E24C53D3212345678(a)解7:A45B66C53D32E2487654321 (8,8)B66C35A54D23E4212345678(b)解8:A54B66C35D23E4287654321 (8,8)C36B65A44D23E5212345678(c)解9:A44B65C36D23E52

圖4　解7～9

87654321 (8,8)B56E25A44C63D3212345678(a)解10:A44B56C63D32E2587654321 (8,8)E57D26A45B64C3312345678(b)解11:A45B64C33D26E5787654321 (8,8)D37C66A45E24B5312345678(c)解12:A45B53C66D37E24

圖5　解10～12

87654321 (8,8)D67C36A55E74B4312345678(a)解13:A55B43C36D67E7487654321 (8,8)E47D76A55B34C6312345678(b)解14:A55B34C63D76E4787654321 (8,8)C66B35A54D73E4212345678(c)解15:A54B35C66D73E42

圖6　解13～15

87654321 (8,8)B46E75A54C33D6212345678(a)解16:A54B46C33D62E7587654321 (8,8)D18C37B56E25A4412345678(b)解17:A44B56C37D18E2587654321 (8,8)D18E47C26A55B3412345678(c)解18:A55B34C26D18E47

圖7　解16～18

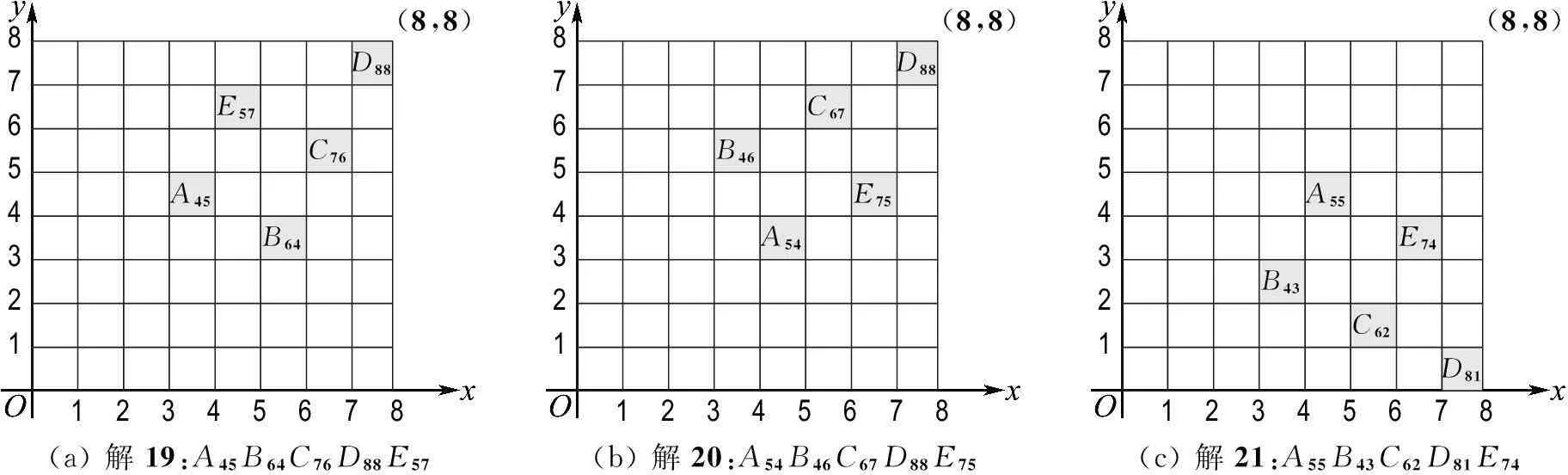
87654321 (8,8)D88E57C76A45B6412345678(a)解19:A45B64C76D88E5787654321 (8,8)D88C67B46E75A5412345678(b)解20:A54B46C67D88E7587654321 (8,8)A55E74B43C62D8112345678(c)解21:A55B43C62D81E74

圖8　解19～21

87654321 (8,8)B65A44C73E52D8112345678(a)解22:A44B65C73D81E5287654321 (8,8)B35A54C23E42D1112345678(b)解23:A54B35C23D11E4287654321 (8,8)A45E24B53C32D1112345678(c)解24:A45B53C32D11E24

圖9解22～24

Fig.9Solutions 22-24

3結語

對于本論題，使用逐步確定皇后最佳(極佳)或剩余最佳(極佳)位置求解五后問題是有效的、成功的．而且，對于類似本論題的2k×2k棋盤問題的求解給出了一種新途徑，它極大限度地克服了以往人們用視察法求解本論題的盲目性．隨著k的增大，收效更加明顯．該成果在防災和安全領域中、在社會管理中，對如何設計必要節點具有理論指導意義，從而凸顯了經濟效益和社會效益．

致謝：在論文完成中，得到了楊元生教授熱情和有益的幫助，在此深表謝意！

參考文獻：

[1] Brualdi R A. 組合數學導論[M]. 李盤林,等譯. 武漢:華中理工大學出版社, 1982.

Brualdi R A. Introductory Combinatorics [M]. LI Pan-lin,etal., trans. Wuhan: Huazhong University of Science & Technology Press, 1982. (in Chinese)

[2]李明哲,金 俊,石端銀. 圖論及其算法[M]. 北京:機械工業出版社, 2010.

LI Ming-zhe, JIN Jun, SHI Duan-yin. Graph Theory and Its Algorithm [M]. Beijing: China Machine Press, 2010. (in Chinese)

[3]李盤林,李麗雙,趙銘偉,等. 離散數學[M]. 3版. 北京:高等教育出版社, 2016.

LI Pan-lin, LI Li-shuang, ZHAO Ming-wei,etal. Discrete Mathematics [M]. 3rd ed. Beijing: High Education Press, 2016. (in Chinese)

[4]李盤林,李立健,劉曉紅,等. 基于啟發性知識研究生院課表編排系統[J]. 計算機學報, 1992, 15(11):876-889.

LI Pan-lin, LI Li-jian, LIU Xiao-hong,etal. A heuristic knowledge-based graduate school timetable scheduling system [J]. Chinese Journal of Computers, 1992, 15(11):876-889. (in Chinese)

Solution to De Jaenisch′s five queens problem

LIPan-lin*1,ZHAOMing-wei1,XUXi-rong1,LILi-shuang1,LIBo-zhang2

( 1.Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China；2.Department of Computer Engineering, University of Waterloo, Waterloo, ON, Canada )

Abstract：The coordinate representation of the chess board is given, the control number or the remaining control number of the queen, and the optimum (heuristical) or the remaining optimum (heuristical) positions of the queen are defined. Using the symmetrical properties of the chess board and through an efficient calculation, the three basic solutions are firstly found, and subsequently all 24 solutions shown in the following illustrations are found. This is the first time that a proof of the minimum number of queens required being five but not four is given, and a completeness proof of the solution has been given.

Key words：five-queen problem; control number / the remaining control number of the queen; optimum (heuristical) or the remaining optimum (heuristical) positions of the queen

中圖分類號：O158

文獻標識碼：A

doi:10.7511/dllgxb201603013

作者簡介:李盤林*(1940-)，男，教授，E-mail:lipanlin@dlut.edu.cn.

基金項目:國家自然科學基金資助項目(61170303).

收稿日期：2015-09-05；修回日期: 2016-04-01．

文章編號：1000-8608(2016)03-0304-05