地下管線測量中獨立坐標系的建立和轉換分析

崔琛(河南省有色測繪有限公司,河南鄭州 450016)

?

地下管線測量中獨立坐標系的建立和轉換分析

崔琛
(河南省有色測繪有限公司,河南鄭州 450016)

【摘 要】當進行地下管線測量的過程中,往往會遇到所提供的圖件資料、控制點不能匹配相關施工要求或者是現(xiàn)有所掌握的資料坐標系統(tǒng)與工程所要求的使用的坐標系統(tǒng)不相同的情況,這也就要求在施工的過程中需要根據不同坐標系之間的坐標進行相互換算或者是建立獨立的坐標系。本文從建立獨立坐標系的必要性入手,探討了多種建立獨立坐標系的方法及其優(yōu)缺點,還就不同坐標系之間的坐標轉換方法進行了討論。

【關鍵詞】地下管線測量 獨立坐標系 坐標轉換

在城市的基礎設施中最為重要的組成部分之一便是整個城市的地下管線，這其中包括排水、電信、供水、電視、電力、工業(yè)管道及燃氣等幾大方面，這些都是使城市可以實現(xiàn)信息傳遞、給排水、能量供給等功能的不可或缺的基礎設施，也是保證人們生活及社會、經濟提高和發(fā)展的基本條件，更是整個城市發(fā)展和生存的物質基礎。在這其中地下管線的相關資料是城市規(guī)劃建設過程中最為重要的信息。如果在城市進行規(guī)劃、設計、管理、施工工作中缺少地下管線的準確的、完整的信息資料，那么必然會影響到整個工程的質量和施工進度，更可能造成重大經濟損失和事故的發(fā)生。因此，要實現(xiàn)城市現(xiàn)代化建設和經濟快速發(fā)展的目標，這一目標的重要工作和基本保障便是完整的城市地下管線測量資料及良好完備的基礎設施。就目前我國大多數(shù)城市的數(shù)據信息管理和地下管線測量都落后于整個城市的發(fā)展腳步，客觀上造成了城市規(guī)劃管理、操作上的不確定性和盲目性，不僅僅對城市未來的可持續(xù)發(fā)展造成了極大的阻礙，還對城市管理和規(guī)劃、建設都帶來了一些制約。因此，我們應當在城市規(guī)劃建設及管理方面充分的認識到地下管線測量在城市發(fā)展中所占有的重要地位和作用。完全弄清城市地下管線的實際情況，這對維護整個城市的正常有序運行，保障人民生活、生產及社會發(fā)展有很重要的作用。

1 工程測量為什么要建立獨立坐標系

在建立獨立坐標系之前先了解下不同坐標系的投影變形值。在高斯平面上長度投影變形的大小與中央子午線的橫坐標值的距離有很強的相關性。有一近似的計算公式：

S=S′+△S＝S′+[y2m/(2R2)]S′

或者△S/S＝y(tǒng)2m/(2R2)

上式中△S/S 為高斯平面上長度變形相對誤差；S為改算到高斯平面上的平面邊長；R為地球曲率半徑；ym為邊兩端點的平均橫坐標值；S′為改算前(橢球面上)的邊長。維度可通過坐標換代來進行計算。30°地區(qū)(緯度不同有異)不同投影帶邊緣的橫坐標值，并由(1)式可計算出長度投影變形值(表1)。

從表1我們不難看出，投影帶的不同其投影變形也是不相同的。投影帶邊緣與中央子午線距離越近，投影變形就越小；反之亦然。如果測區(qū)位于國家分帶的中央子午線左右45 公里以內時，投影變形小于1/40000，工程的坐標系就可以使用將國家分帶來充當，當然也可以直接利用國家點的坐標數(shù)據來進行平差計算。如果測區(qū)位于國家分帶的中央子午線左右45 公里以內外的情況下，為了達到投影變形的標準，我們就必須建立工程獨立坐標系，同時縮窄投影帶寬度。此外高斯長度投影變形除了與其有關的因素還有歸算高程面高差相關聯(lián)。在工程測量中常規(guī)都是要求投影變形要小于1/40000(即2.5cm/km)。

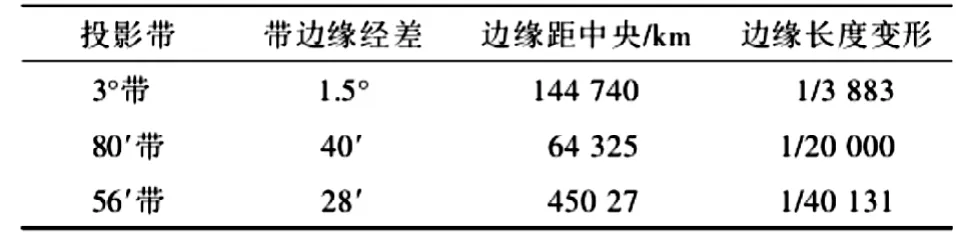
表1　投影變形值

一般在進行地下管線測量之前，還應該收集被測區(qū)域已知的地形資料、控制點、設計圖、調繪圖、竣工圖及施工圖等等，對于未知的區(qū)域即沒有地形圖及控制點，往往還需要建立施測地形圖及基本控制網。當某些地區(qū)的控制資料與甲方難以協(xié)調時，設計圖、調繪圖、竣工圖及施工圖等相關資料就屬于不同的坐標系，為了能按時完成施工要求，因此就需要技術人員建立獨立的坐標系同時進行坐標轉換工作。

坐標系統(tǒng)的選擇是否合適關乎到整個工程的質量好壞，因為所有的前期測量結果都是建立在同一坐標系統(tǒng)的基礎上而進行的。在管線探測工程布設測量控制網時，對它的成果有很多的要求，不僅應該滿足大比例尺與竣工測量、地下管線放線測圖需要，也要滿足地下管線數(shù)字測量相關要求。經上述測量到的相關數(shù)據計算后在應用到實際當中，但是施工放樣的時候就需要控制網實測的長度與標反算的長度盡最大的可能相符合。在管線探測工程布設測量控制網時，第一步就要確定所要采用的坐標系統(tǒng)。在《工程測量規(guī)范》中有相關規(guī)定：面控制網的坐標系統(tǒng)，應滿足測區(qū)內投影長度變形值不大于 2.5cm/km。為了這樣計算得出的長度在實際工程應用中無需變更，就要求減小高程規(guī)劃與投影變形控制在相對小的范圍之內，兩者的相互影響是建立獨立坐標的重要作用。

2 獨立坐標系統(tǒng)的建立

在通常情況下建立獨立坐標系統(tǒng)的時候，要以國家等級控制點作為獨立坐標系統(tǒng)的起算數(shù)據。原因之一是國家等級控制點的可靠性很高，在成果進行相互之間的利用和轉換之時也非常方便，而且控制點的所有數(shù)據也都可以為建立獨立坐標系統(tǒng)的時候提供某種意義上的參考數(shù)據。如何選擇中央子午線的最佳位置以及抵償高程面的最佳位置是建立獨立坐標系統(tǒng)的過程中必須要注意和考慮到的，為的是保證所建立的獨立坐標系統(tǒng)的正確性。如果是以測區(qū)中心為中央子午線來建立獨立坐標系統(tǒng)時，為了達到所測區(qū)域的范圍盡可能的擴大化，在建立的過程中就應該下移投影面的位置。但是如果是使用抵償高程面作投影面建立獨立坐標系統(tǒng)的時候，需要考慮到的因素就相對較多，例如測區(qū)的高低起伏情況、測區(qū)距中央子午線的位置等等。下面介紹3種常用的建立獨立坐標系統(tǒng)的方法：

第一種建立獨立坐標系統(tǒng)的方法；采用抵償高程面的方法建立獨立坐標系，抵償高程

面的計算方法如下：

hm=Hm-Y2m/2Rm

式中：Hm—觀測邊的平均大地高(計算時近似取觀測邊的平均正常高代替)；Ym—高斯平面上距中央子午線垂距的平均值；Rm—抵償高程面高程。

假設某一待測區(qū)域高程平均為1000m，其中測區(qū)中央與中央子午線距離為40km，設Rm=6378.2km則hm≈875m。也就是說在中央子午線不變的前提下，將高程歸化面提高到875m，可使測區(qū)中央的兩項改正接近于零。該坐標系可控制的東西跨度用以下公式計算：

△Ym= 2R2m(X+(Hm-hm)/Rm)

公式中：X—為兩項投影改正的相對誤差；取X=1/40000，將上面假設數(shù)據hm≈875m代入上式：△Ym=60.2km。

上述例子表明，測區(qū)距中央子午線的遠近與控制的東西跨度范圍成反比。

第二種建立獨立坐標系統(tǒng)的方法；將中央子午線移到測區(qū)中央可以達到讓測區(qū)的兩項改正在測區(qū)中央幾乎為零的目的，把歸化高程面提高到該測區(qū)的平均高程面上，建立任意帶高斯正形投影平面直角坐標系。若要達到離中央子午線40km以內的地區(qū)其兩項改正的影響在每公里2.5cm以內，則必須要測區(qū)高差起伏在100m范圍內就可以。最適合工程建設地區(qū)需要的就是這種地方獨立坐標系，所以，只要工程建設區(qū)域的面積不是很大，東西跨度在80km就可以滿足要求。如果是在小于80km測區(qū)的范圍內，上述的方法就不合適了。

第三種建立獨立坐標系統(tǒng)的方法；采用不變動高程歸化面建立獨立坐標系，就可以有效的避免上述建立獨立坐標系復雜的計算過程。這一方法只需要通過移動中央子午線就可以完成建立獨立坐標系。用下式可以計算出中央子午線距測區(qū)中央西移的距離：

Ym=2RmHm

3 坐標系統(tǒng)轉換

3.1 坐標系之間的轉換

不同投影面間坐標的換算需要經過下面兩個步驟，首先一個投影面上的直角坐標轉換成國家坐標系統(tǒng)的大地坐標。其次將第一步中轉換好的大地坐標轉換成另一投影面的獨立坐標。

3.2 坐標系分類

(1)參心坐標系。現(xiàn)階段比較常用的坐標系是1954年、1980年的北京坐標系和西安坐標系。(2)地心坐標系。采用WGS84大地坐標系。(3)獨立坐標系。包括原點、定向在內都是自己的，有與當?shù)仄骄０胃叱虒膮⒖紮E球。

4 結語

在獨立坐標系的實際建立過程中，要求盡可能的選擇使用最簡便方法來建立獨立坐標系，盡最大的努力使測區(qū)內投影變形值最小，若要達到這一目的就需要在測量過程中全面綜合的考慮各種因素，比如高差起伏、測區(qū)的地理位置等。由于建立獨立坐標系統(tǒng)的起算數(shù)據為國家等級控制點，計算所使用的參考橢球參數(shù)，因此其可靠性很高，也更有利于成果之間的相互利用和轉換。在測區(qū)測量中坐標系的轉換和選擇，不管采用上述三種方法的哪一種建立獨立坐標系，都需要滿足所有測量的要求及相應規(guī)范，對于施工控制網最重要的是坐標反算的邊長與地面實測的邊長要相等。

參考文獻:

[1]GB 50026-2007,工程測量規(guī)范[S].

[2]CJJ/T8-2011,城市測量規(guī)范[S].

[3]CJJT73-2010,衛(wèi)星定位城市測量規(guī)范[S].

[4]傅文祥,姜道利,潘寶玉,欒繼福.城區(qū)獨立坐標及基本控制網的建立[J].測繪通報,2002(S1).

[5]施一民,李建,周擁軍,張文卿.地方獨立坐標系的性質與區(qū)域性橢球面的確定[J].測繪通報,2001(9).

[6]劉大杰,施一民,過靜珺.全球定位系統(tǒng)的原理與數(shù)據處理[M].同濟大學出版社,1996.