線性回歸法在爆破測振分析中的應(yīng)用
言旺軍 周余奎(中鐵西南科學(xué)研究院有限公司,四川成都 610031)
?
線性回歸法在爆破測振分析中的應(yīng)用
言旺軍 周余奎
(中鐵西南科學(xué)研究院有限公司,四川成都 610031)
【摘 要】本文討論了如何采用線性回歸的數(shù)學(xué)方法來求解傳統(tǒng)的爆破振速計算公式-薩道夫斯基公式中的K、α值的方法,以及如何將其與神經(jīng)網(wǎng)絡(luò)模型相結(jié)合進行進一步優(yōu)化的方法,使得常用的薩道夫斯基公式的預(yù)測值與實測值更加相吻合,達到預(yù)測爆破震速的目的。作者并將這一計算方法結(jié)合一工程實例進行了驗證,計算值與實測值比較接近,該方法達到了對該項目進行安全預(yù)測的目的。
【關(guān)鍵詞】線性回歸 爆破測振 神經(jīng)網(wǎng)絡(luò)模型
【Abstract】This paper discusses how to use linear regression mathematical methods to solve the traditional formula of blasting vibration velocity the Sadaovsk formula of K, alpha value method, and combining with the neural network model for further optimization method, makes the commonly used Sadaovsk, more consistent formula of the predicted and the measured values, to achieve the purpose of predicting blasting vibration velocity.The author used the calculation method combined with an engineering instance verified and calculated values and measured values is close, so this method achieved the purpose of safety projections for the project.
【Key words】Linear regression Blasting vibration monitoring Neural network model
1 引言
在民房、邊坡及井巷等重要的建筑物或構(gòu)筑物附近進行較大規(guī)模的爆破施工時,一般需要進行爆破震動的跟蹤監(jiān)測,并依據(jù)設(shè)計中給定的控制標(biāo)準(zhǔn),進行爆破安全校核和爆破參數(shù)的修改調(diào)整,以達到控制爆破震動的目的。目前,判定爆破震動對地面建筑物和構(gòu)筑物的影響,可用質(zhì)點振動的位移、加速度、或速度等指標(biāo)。而大量的工程實踐及監(jiān)測成果表明,質(zhì)點振動速度比振動加速度或位移與結(jié)構(gòu)的爆破震動破壞有更良好的相關(guān)關(guān)系。因此,國內(nèi)外普遍以質(zhì)點振動速度作為爆破震動控制安全標(biāo)準(zhǔn)。振速的計算一般用薩道夫斯基公式,而有些人認為用此公式計算存在很大的誤差,其原因在于K、α值的確定存在很大的局限性,為此,筆者提出了一種完善K、α值的方法。近年來,隨著計算機技術(shù)的提高,數(shù)值模擬方法的迅速發(fā)展以及神經(jīng)網(wǎng)絡(luò)的日益成熟,用他們處理爆破問題使爆破參數(shù)愈來愈完善,也使得準(zhǔn)確預(yù)測質(zhì)點的振速成為可能。在此,借用這方面的知識,用計算機來計算K、α值,并運用K、α值來預(yù)測同一地質(zhì)條件下的爆破震動。
2 質(zhì)點振動速度控制安全標(biāo)準(zhǔn)
地面建筑物和構(gòu)筑物來說,爆破而引起的質(zhì)點振動速度可按下式計算:
式中Q----同段起爆的最大藥量,
R----爆源至計算點之間的距離,
α----同地質(zhì)條件有關(guān)的地震波的衰減系數(shù),α=1-3。
K----同巖石性質(zhì)、爆破方法等因素有關(guān)的系數(shù),一般取值為50-200,巖土松軟時取大值。
可在現(xiàn)場經(jīng)小型爆破試驗來確定α和 k的值。
各國不同學(xué)者對安全振速規(guī)定的值不同。《中華人民共和國爆破安全規(guī)程》中的判據(jù)為:
(1)一般磚房、非抗震的大型砌塊及預(yù)制構(gòu)件房屋、構(gòu)架建筑為2cm/s;
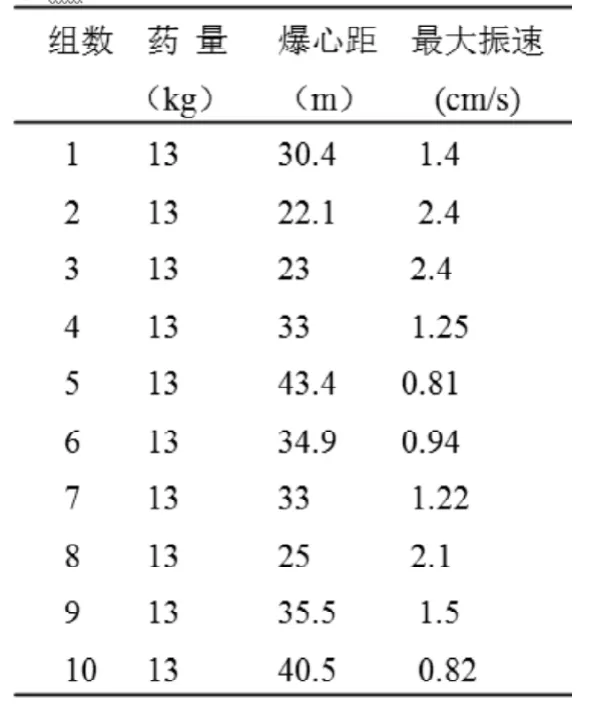
表一:
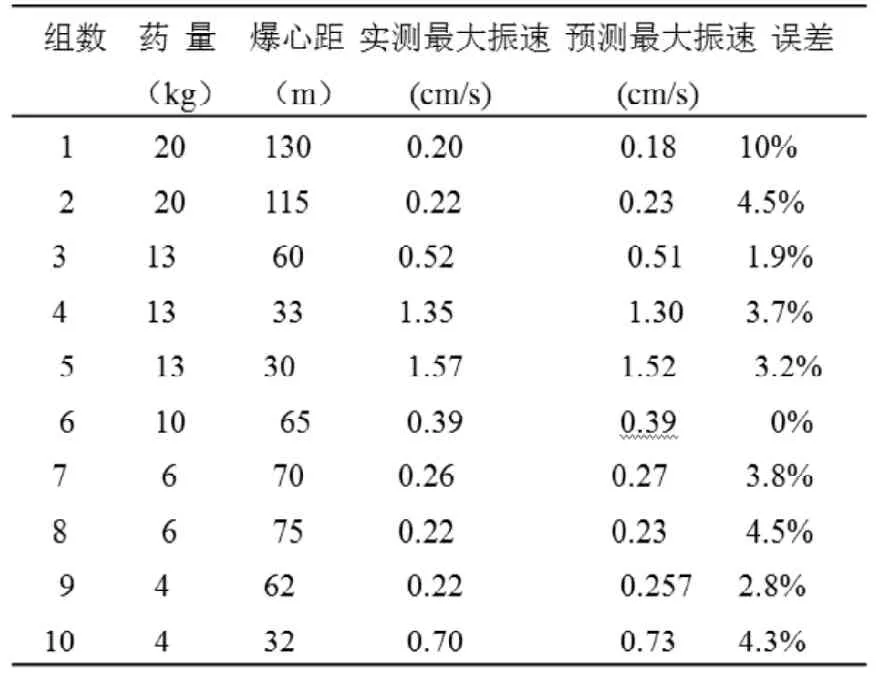
表二:
(2)鋼筋混泥土框架房屋及修建良好的木屋為5cm/s;
(3)隧洞為10cm/s;
(4)礦山巷道中圍巖不穩(wěn)定、有良好支護時為10cm/s;礦山巷道中圍巖中等穩(wěn)定、有良好支護時為20cm/s;礦山巷道中圍巖穩(wěn)定而無支護時為30cm/s。
3 爆破地震波的神經(jīng)網(wǎng)絡(luò)模型
在此利用一元線性回歸模型求α,b的估計值:
已知變量的 n 組試驗值(xi,yi),=1,2,,用最小二乘法求出α,b的估計值。
作離差平方和:
選擇參數(shù)α, b使Q達到最小值,即
為此,令分別對α和b的兩個一階偏導(dǎo)數(shù)等于零,即
變形為
因為解方程組得到的不是α,b的真值,而是它們的估計值,所以可把方程組中α, b分別用,估計值代替,得到
并將上面方程組中每個方程的兩邊除以 n 得
解此方程組得
由于開始測出前n組數(shù)據(jù),即有n組V,Q和R已知,也即是有n組y,x已知,在利用一元線性回歸模型求出b和α,反求出α,k。
本神經(jīng)網(wǎng)絡(luò)模型的流程圖如圖1:
4 計算結(jié)果與分析
今筆者正進行一項測震工程,取得多組數(shù)據(jù)。任選測得的10組振速、藥量和爆心距的數(shù)據(jù)樣本(見表一),對網(wǎng)絡(luò)模型進行訓(xùn)練。
之后,開始預(yù)測,和實地測震同時進行,把預(yù)測的數(shù)據(jù)與實地測的數(shù)據(jù)比較,看其誤差大小(見表二)。并把實地測的數(shù)據(jù)從輸入層輸入程序,使網(wǎng)絡(luò)模型進行自學(xué)習(xí),以保證以后的K,α值更加完善,使其誤差更小。
從表二中可以看出,預(yù)測值與實測值之間的誤差較小,并且對同段藥量誤差有減小的趨勢。
5 結(jié)語
(1)爆破引起的振動的質(zhì)點的最大振速與藥量成正比,與爆心距成反比,即驗證了薩道夫斯基公式。
(2)由于采用了神經(jīng)網(wǎng)絡(luò)模型,使得K、a的值在自學(xué)習(xí)過程中不斷的完善,從而使薩道夫斯基公式更加準(zhǔn)確實用。但是由于筆者在進行測震時,儀器有限,布點布在較小的范圍內(nèi),測得的數(shù)據(jù)有限制,對于大范圍的預(yù)測,可能有較大的誤差。
參考文獻:
[1]陶松霖,編.《鑿巖爆破》.冶金工業(yè)出版社,1986.
[2]張繼春.三峽工程基巖爆破震動特性的試驗研究,爆炸與沖擊, Vol21.No2.2000.4.
[3]Richard Mansfield 著,廖衛(wèi)東,趙軍 譯,Visual Basic 4.0編程手冊.機械工業(yè)出版社.
[4]汪榮鑫,著.數(shù)理統(tǒng)計,西安交通大學(xué)出版社,1986.10.

