對數學基礎的0和1的新認識

陸道淵(浙江溫州 325000)

?

對數學基礎的0和1的新認識

陸道淵
(浙江溫州 325000)

【摘 要】發現并使用“實數”新概念,消除了理學中一切有關的重大悖論(請注意:學術研究中的矛盾一詞,實質上分兩種概念,必須要分清:(1)一個命題自我否定,簡稱悖,必錯;(2)兩個命題的互相否定,哪個錯未確定。所以命題有 悖 就自我否定而不成立。和疑難,并展示了消悖實例,使數學、理論物理學徹底淺簡了。

【關鍵詞】總段1 〈自然數〉 〈量數〉 〈整數〉

學習和研究數學、物理學的人都知道，現行理學中有很多重大悖論和疑難；連邏輯主義數學家弗雷格也說‘邏輯在哪里出了毛病呢？很多人百思不得其解。這一問題直接威脅到數學的基礎………更重要的是，威脅到自然數的定義。’還說‘對什么是1這樣一個貌似簡單的問題，尚未有一個完滿的答案……否則，我們最終將弄不清楚負數、分數或復數。’(引自［3］)

數學家們也都哀嘆數學的悖論災難越來越深重了；有些數學家試圖用“零(記為0)和無限大(記為∞)是關于1的反演點，即0∞＝1”的方法(引自［1］的第8頁)來躲避如影隨形的悖論，但更不通了，因為現行的所謂“實數”已(無理的)規定“0是整數、偶數，但不能做除數”；而且0既然是“實數軸”的始點，而∞卻在無限的遙遠，也不是真正的反演。明擺著，是“實數”有毛病，即“實數軸”為無限的直線是錯誤的。

令人驚喜的是，如把“實數軸”改為有限的線段，則整個現行數學基礎就被革命性糾正，從而所有相關的悖論和疑難也隨之全部消除。

于是，所謂“實數”就有了其新概念〈數〉 (用〈〉 表 示 新概念)。

1 “實數”的新概念

先取“實數軸”的正半軸射線改為線段 ，再把它有限等分，并把有序性編號①、②、③…從左向右標在相應的分點上，則1、2、3…等稱為有序積段，而①、②、③…是其分點的 編號，如圖1。對這同一線段，當有序編號n 增多，則等分分段△n間隔縮小，但△n≡1‘(固符’△專使△n≡1)，如圖2。

圖2顯示出四點：第Ⅰ、總段(總段用粗體1標志，以區別于積段1)的始點是0 ；0 是0的編號；第Ⅱ、如果反序讀正半軸的n，則也出現負號，這說明正負符號與有序積段n本身無關(例如錢這數量，其本身是沒有正負的，只在使用時才出現正負號。)；第Ⅲ、如把每一分段△n繼續不斷十等分，則n →∞，但n ≠∞，否則△n＝1/ ∞=0，總段就不存在了，這就有悖 ；這也證實了∞不屬于總段1，即n 和∞分別是1和∞兩者界點的編號。所以編號為∞的∞不在總段1上，而是總段1的終端n 之外的空間。注意，同一界點的兩個編號∞和n 是不容許換位的；但現行的“實數軸”是無限的射線，才使數學家們把∞和n 合二為一了，即可以n ＝∞了，這是“實數”有缺陷的根本原因； 第Ⅳ、不管編號n 如何增多，恒有△n＝1，即等分分段△n≡1。

同理，現用的負半“實數軸”用上述辦法也可顯出圖2這四點，如圖3。

由四個圖可知，0是不真的數，因為它沒有長度，因此0在新概念中僅表示‘無’‘、空位’等。由圖4可看出，0是微觀的‘無’，∞是宏觀的‘無’，作為數都是不真的。要有總段1，才能被有限多的編號n 等分后得到有限多的有序積段n；如果沒有總段1，就會把有序編號n與有序積段n混而為一了。

注意：事實上總段1不是〈自然數〉的1，因為它不是由等分得到，因而沒有編號，所以不是〈數〉。

不連續的〈自然數〉叫〈整數〉。所以〈整數〉中沒有正號、負號和不真的〈數〉0、∞ 。

數學范疇不能引入各種量，因而沒有量綱(量綱即量度單位)，以致人們不會區別〈純數〉和〈量數〉兩個概念，現在有了新概念〈自然數〉，就可區別〈純數〉和〈量數〉了，例如mn 和m/n ，雖然兩者都是〈自然數〉之間關系性式子的〈數〉，但前者是〈純數〉而后者是〈量數〉。

進而，一切小數無論是‘有理的，無理的，或超越的’，實質上都是物理元素間或幾何元素間的關系的值，亦即僅由〈自然數〉n(n是其編號)間按各種關系性運算符號組成的式子產生，如0.6 =3/5、0.42857=37、1.4142……=、π＝L/D【注意，在沒有量綱/的條件下，L，D都只能是(存在性的〈)整數〉，不可能是(關 系 性 的)小數；因為總可以用最小的度量單位，能使小數點消去。】、e=1+1/2!+……1/n!，等。有了新概念〈自然數〉，就知道任何小數在表達上都沒有獨立性(須由〈自然數〉組成的式子表出)，而且甚至沒有完全性(如無限小數須取近似值)，所以都不能標在新概念數軸上。有了〈自然數〉，還容易區分無限小數中的“無理性和超越性”，如無限小數、無理數3/7、這兩式中的〈整數〉是確定的，而L/D 、1+1/2!+……1/n!中〈整數〉是不確定的，這就是e、π為何具有‘超越性’的原因。顯然，這一判斷方法是簡明有效的(而康托的用數軸判斷法是錯誤的，因為凡小數都是關系性的數，在數軸上是沒有的)。

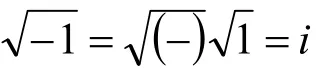
概括上述，總稱為“實數”的含義不合事實，應改稱為〈數〉，表示新概念：〈數〉包括由總段1所產生的真的數〈自然數〉n和其編號

還須提醒四點：

(1)既然在新概念的數軸上，不存在各種小數，所以還證實了與“實數”相關的所謂“開區間”、“閉區間”也是假概念，由新概念編號n 取代，，這極大的淺簡了高等數學。

(2)函數關系性(不管是幾何關系或是物理關系)的〈數〉，不是坐標軸(坐標軸 由數 軸 組成)上本身所有的存在性的〈數〉。所以，坐標軸上只能標上存在性的〈數〉即新概念〈自然數〉；當用到不同函數式的分數、小數和無理數時，只能臨時在軸上點出。

(3)上述證實了，客觀只存在‘線段’，即‘線段’是真概念，而‘射線’和‘直線’應分別是‘一個端點暫未確定的線段’和‘兩個端點都暫未確定的線段’的簡稱。

2 解決現行數學中幾個已公認無法解決的悖論和疑難的實例

(1)“整體等于其局部”悖論和對其解決：現行科教書依據所謂“實數”，用康托的“一一對應法和勢的大小”證出“自然數與其正偶數(或正奇數)一樣多”，從而得出“整體等于其局部”。

解決：由于新概念〈自然數〉是有限的，即知這是悖論。

(2)“康托集”悖論和對其解決：現行科教書關于“康托集”的表述是(引自［2］363頁和366頁)：“把區間 [0，1](即長度為1的線段)三等分，棄中間子區間(1/3，2/3)；如此連續棄中，問棄的數多還是剩的數多？”，“經運算，所棄的子區間之和的長度A=1；但還剩點集X，其元素(即長度為零的點)有無窮多；用一一對應法，點集X的元素與長度A中的元素一樣多”；“與我們的習慣思維似有矛盾……全部區間都扔掉了，但像沒扔掉。”

上面引文顯示，編著者實際已承認了其“證明”是悖論；事實上，所棄的和還剩的都不是“點集”而是‘段集’(即其元素都是長度不為零的小線段)。

解決：用新概念〈自然數〉，所謂“區間 [0，1]”(注意，有了〈自然數〉的‘編號’“，區間”已被‘編號’取代，即所謂“開區間”“、閉區間”已被否定)實即總段1，其終點編號n ≠∞，即所棄的“子區間”總長度為A，而所剩的區間之和的長度為a；所以A遠大于a。于是該悖論解決。

(3“)連續統假設”悖論和其解決：現行科教書已承認了該“假設”是無法解決的第一難題。

解決：由新概念〈自然數〉知，該“假設”是“整體等于其局部”悖論的一般化，這等于已得到解決。

(4)羅素悖論的解決：羅素在研究自然數時發現了羅素悖論‘：集包含自身為元素’。第三次數學危機由該悖論的提出引起；至今沒有解決。

解決：如用新概念的〈自然數〉，因總段1不是積段的1，即總段1不是〈數〉，就不會‘集包含自身為元素’，于是 羅素悖論即得解決。

(5‘)費馬大定理’(即xn+yn=zn，當n〉2時，無正整數解)疑難的解決：現行科教書依據現行“實數”概念，宣稱該‘定理’由懷爾斯在1995年成功證明，但數學家們都認為懷爾斯的證明太冗長、不淺簡，因而其證明性不強(注意，費爾馬在關于這不定方程的待求正整數解這頁的空白處寫道‘：…………我已發現了這個美妙證法，可惜這里的空白地方太小，寫不下。’；這證明費爾馬的‘美妙證法’是很簡短的。)

如用新概念〈自然數〉，可簡潔證明如下：

所以，失逸的費爾馬的‘美妙證法’，必是這種證法。

(6)現行教科書中兩個疑似已解決的著名悖論(即‘莊子悖論’和‘芝諾悖論’，請看［1］的第3和第9頁)， 其實并沒有真的解決，原因就是沒有積段n和分點編號n 之分，即雖知n →∞，卻不知n≠∞，把n 和∞∞兩個編號混同了，才說出“無限段路程之和可以是有限量”(引自［1］的第3頁末；注意，此話是具體、清楚的低劣錯誤，出于數學家之口，實為數學的悲哀)這種有悖的“結論”，從而沒能真正解決這兩個悖論。所以，只有知道新概念〈自然數〉 n是有限的，即n →∞但n ≠∞，表達了n 僅具‘未知性’而不具‘無限性’，從而不會把n 與∞混同(由圖2或3更可直觀看出，總段1的終點是n與∞的界點，并標著n 、∞，很容易混同)，才使這兩個著名悖論得到真正的徹底解決。

所以，這實例6，應概括為一句直觀而淺簡的實質性表述：總段的n是積段，而每分段恒為1，于是有n÷1＝n ，這編號n 就有限；當此確定線段被長度為0除，有n÷0＝∞，即得編號等于∞；于是

(為簡，更多實例，略。)

顯然，使用“實數”的新概念〈數〉，能消除悖論而沒有不良副作用。

參考文獻:

[1]張景中主編,梁昌洪編著.《話說極限》.書號為ISBN 978-03-023788-0 科學出版社出版.

[2]張景中主編,王樹禾編著.《數學聊齋》(第二版).書號為ISBN7-03-013958-5.科學出版社出版.

[3]趙敦華編著.《當代英美哲學舉要》.書號IBSN7-80092-552-8當代中國出版社出版.