求均質桿件動能的一種新方法
——矢量運算法
朱章根(韶關學院物理與機電工程學院,廣東韶關 512005)
?
求均質桿件動能的一種新方法
——矢量運算法
朱章根
(韶關學院物理與機電工程學院,廣東韶關 512005)
【摘 要】動能定理一直是力學教學的一個重難點,同時也是一個很重要的內容。后續的分析力學基礎都是以動能及勢能為基礎的,可見其在力學課程中的重要性。我們提出一種計算桿件動能的新方法并且對新方法給出了理論證明。與常規方法不同的是新方法運用基礎力學知識求出桿件兩個端點的速度繼而用基礎矢量運算可輕易求出其動能表達式。并且給出了該新方法在多種動力學問題中的應用。
【關鍵詞】矢量 均質桿 動能 動力學 拉格朗日函數 分析力學
桿件運動時其動能為標量,速度為矢量。而二維矢量點積為一個常數,直接根據矢量的運算是可以直接得到標量的。根據矢量運算可以繞開柯尼希定理,直接求出平面均質桿件做平面運動時的動能。因而可將動能直接表示成為矢量運算形式。
定理描述如下:假如一根長為l的均質直桿在做平面運動,m為桿的質量。其兩個端點A、B的速度矢量分別為u、v,矢量的點積為u·v則該均質直桿的動能為
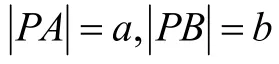
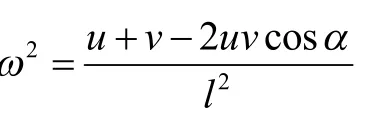
將上式以及u =aω且v =bω,帶入動能表達式,可得
即(*)式成立,由以下幾個例題可以看出它在動力學之中的應用。
例1 兩個長均為l質量均為m的均質桿在A點銜接后懸掛在O軸上,在B端受到沖量S的作用,如圖2所示,求碰撞后兩桿的角速度。
解:取OA桿的轉角ψ1和AB桿的轉角ψ2為廣義坐標。碰撞前兩桿的角速、均為零,碰撞后兩桿的角速度分別為ω1和ω2。桿OA作定軸轉動,故端點O的速度大小為vO=0,端點A的速度大小為vA=Lω。此時0,故其動能為
因此系統的動能為
碰撞前廣義動量都是零,碰撞后的廣義動量為
由此解得
例2:在例1的基礎上,均質桿和OA以及AB用鉸A連接,用鉸O固定,如圖二所示。若兩桿的長度不相同分別為l1和l2。質量也不同分別為為m1和m2。在B端作用的不是沖量而是一個常值水平力S則該系統的運動微分方程為何?
解 這種問題一般用拉格朗日方程求解,勢必需要求該體系的動能。因系統具有完整理想約束,具備拉格朗日方程求解的條件。系統具有兩個自由度,取α,β為廣義坐標。主動力包括P1,P2,S。兩個重力是有勢力,而常值主動力S可以當作重力對待。由于OA桿繞O點作定軸轉動,O點的速度為0,端點的A的速度大小為vA=l1。因此OA桿動能為
故整個系統的動能為
接著求系統的勢能,根據幾何關系有
因而總勢能為
系統的拉格朗日函數為
由
可得系統的運動微分方程為:
例3 一根長為l均質細桿AB質量為m,靜止直立于光滑水平面上。當桿受微小干擾而倒下時,設桿與地面的夾角為θ。求桿在下落過程中未與地面碰撞前任意時刻的角速度以及桿剛剛躺到地面前瞬時桿的角速度。
解:由于地面光滑,直桿沿水平方向不受力,水平方向上動量守恒。因而直桿在倒下過程中其質心將鉛直下降。當直桿在下落的過程中,約束力不做功,僅由重力做功,系統的機械能守恒。設A點的速度矢量為u,B點的速度矢量為v有幾何知識易得
將u、v以及uv帶入()*式可得
初始時動能為T0=0。則由動能定理可得
繼而有桿剛剛躺到地面前瞬時,此時θ=0,將θ=0帶入上式,根據()*式,此時桿的角速度為
也可以這樣求,桿剛剛躺到地面上之前瞬時,A點為桿的瞬心。則B點的速度為θ.l,可得到同樣的結果。
參考文獻:
[1]李俊峰等.理論力學(第2版)[M].北京:清華大學出版社,2010.
[2]哈爾濱工業大學理論力學教研室編.理論力學(第7版)[M].北京:清華大學出版社,2009.

