類比思想融入《復變函數》教學的研究與實踐

李紅光

（懷化學院數學與計算科學學院，湖南懷化418008）

類比思想融入《復變函數》教學的研究與實踐

李紅光

（懷化學院數學與計算科學學院，湖南懷化418008）

從教學改革和培養應用型人才的全局出發，結合教學實踐，論述了把類比思想融入到《復變函數》教學中的重要性，并且就如何實現類比思想融入到復變函數教學過程中的具體方案進行了探討，希望能為以后的《復變函數》課程的教學改革提供一定的幫助.

類比思想；復變函數；教學改革

1 引言

《復變函數》是繼數學分析之后的一門重要的分析課程，是高等院校數學專業和物理學專業的必修課程和主要課程.《復變函數》主要包括了復極限、復積分、復級數和留數理論等知識點[1-2]，其中復極限、復積分、復級數與數學分析中的極限、積分、級數[3-4]有著千絲萬縷的關系。如何通過教學，幫助學生了解這種聯系，讓學生更好地理解復極限、復積分、復級數等概念，為其它后續專業課程的學習打好基礎，又使學生在學習這門課程的過程中培養邏輯思維能力、類比能力和研究能力。而類比思想以其獨有的眼界為復變函數的教學提供了新的理解，這對學生更系統地掌握復變函數的基本理論有很大的幫助，對提高復變函數的教學效果有著深遠的影響。

2 類比思想融入教學中的重要性

類比思想，又稱類推思想，是指由一類事物所具有的某種屬性，可以推測與其類似的事物也應具有這種相同屬性的推理思想。類比復變函數與數學分析的概念，不僅要抓住概念的本質，弄清概念的真正含義，即區別其它概念的特有性質，而且要理解概念的各種條件和理清結論；不僅要比較與數學分析中概念的異同，而且要比較復變函數概念間的異同與相互聯系，真正把理解和掌握基本概念作為學好復分析的首要任務，做到靈活應用相關的基本概念。

本人從事復變函數課程教學已有多年，認為類比思想是可以融入到復變函數教學的各個方面中的.實踐證明這種融入對復變函數的教學有著非常好的效果.在復變函數課程教學過程中融入類比思想，有助于學生更好地掌握數學分析和復變函數的聯系；有助于學生更好地了解和掌握復變函數課程的基本內容、概念和方法；有助于學生比較直觀地理解一些基本定理，靈活地運用復變函數的知識解決相關問題。而類比思想可以把復變函數教學的重點轉移到“背景——類比——推斷——解釋——啟發”上，并可使學生將“知識”迅速轉化為“能力”，復變函數不再是抽象難懂、深不可測、高不可攀、望而卻步的“難學難用”的課程了.這可使學生的數學素質、用數學的能力得到大幅度提升.

3 類比思想融入到復變函數的整個教學過程

3.1 融入到課堂教學

復變函數中包含很多與數學分析相似的概念和定理.因此，在復變函數課堂教學過程中，如何讓學生通過類比數學分析的知識來掌握這些抽象的概念和定理變得尤其重要.對于復變函數的教學，以往的方式是注重概念的數學表達和邏輯方式，這樣的方式讓學生覺得復變函數的概念繁多、無趣和難以理解.現在我們可以在概念和定理的講授中融入類比的思想，從而改變以往的教學方式，可取得很好的教學效果.其實，復變函數中的眾多概念與定理，如極限、導數、積分、級數都是可以從數學分析中的極限、導數、積分、級數等概念和定理類比過來，這樣學生就會感到課本里的概念和定理不再是那么陌生，而是似曾相識的，也不再感到這些概念抽象、難懂了.這種融入類比思想的教學方法，有助于培養和造就學生的認知能力和創新能力.

例如，在復變函數可導性（從而判斷函數解析性）的充要條件中，為什么要求函數的實部和虛部必須滿足Cauchy-Riemann方程？

先引導學生通過數學分析導數的定義和復變函數導數的定義去思考問題，啟發學生自己去解決問題，發現其中的本質.

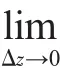
又如，一元實函數的微分中值定理能推廣到復變函數中來嗎？

引導學生用Rolle定理和復指數的知識考慮問題，從而達到學生能用數學分析的相關知識推導復變函數的知識.

答：不能。我們僅以Rolle定理為例來說明。一元實函數的Rolle定理是說，若y=f（x）在閉區間[a，b]上連續，在開區間（a，b）內可導，并且f（a）=f（b），則至少存在一點ξ∈（a，b），使f′（ξ）=0.該定理不能推廣到復變函數的原因如下：

（1）討論復變函數w=f（z）在點處的連續性與可導性時，要求該函數定義在z0的某個鄰域（或的某個區域）上，僅在實（或虛）軸的某個區間上不能討論連續性與可導性，即使定義在復平面內某個以z1和z2為端點的線段上也不行.

（2）若將Rolle定理的前兩個條件放寬為f（z）在復平面的某區域D內解析，將第三個條件f（a）=f（b）改為f（z）在D內某線段的兩個端點z1與z2上相等，即f（z1）=f（z2），結論也不一定成立.例如，設f（z）=ez，根據復指數函數ez的周期性，對任何z∈D，ez=ez+2kπi（k為整數），但由于（ez）′=ez≠0，所以在以z1與z2為端點的線段內，沒有一點使（ez）′=0，故Rolle定理不成立.

3.2 融入到實驗教學

伴隨著計算機的飛越發展和數學軟件（如Mathematica，Matlab）的迅速成長，許多與數學相關的實際問題的解決都需要通過計算機來完成.目前，數學與計算科學學院正在探索專業課程的教學改革，復變函數課程也納入了該改革中.結合以往的實踐教學改革，認為在復變函數的教學過程中增開實驗課，不但可以提高學生對復變函數的興趣，同時還可以增強他們的實際動手能力.復變函數的實驗一般要結合物理應用背景，以數學軟件為工具，模擬實際環境進行教學.在復變函數教學中，可開設2～3次實驗課，主要是讓學生利用類比的方法來解決復變函數方面的一些實際問題，從而達到提高學生的積極性，創造性和解決問題的能力.

3.3 融入到課后作業

在以往的復變函數教學過程中，給學生布置的作業基本上是出自于書中的課后習題，然而，課后習題陳舊、形式缺乏、應用性嚴重不足，這嚴重地影響了復變函數的教學效果.因此，僅僅布置課后習題作為學生的作業，不能很好地培養學生對實際問題解決的能力和動手能力.為改善這種不利的局面，在作業的布置上亦可融入類比的方法，適當增加一些開放性的課后作業，如可以安排一些與數學分析知識相關的復變函數問題，這樣可以培養學生的遷移能力、創新能力；也可以增加一些利用數學軟件能完成的復變函數方面的應用題，從而達到對學生的實際應用能力的培養.

3.4 融入到考試考核

以往對復變函數課程考核就是采取閉卷考試，而且考試題目或者是出自于書中的例題和課后的習題；或者是出自于書中的某些基本概念和定理.這樣的結果是只能考查學生的識記能力，而無法考查學生的遷移和應用能力，從而直接導致很多學生高分低能，學生無法在復變函數學習過程中理解和提煉數學思想和方法.這樣方式與復變函數教學的初衷是相違背的，也與我校所提倡的應用型人才培養模式相違背的.考慮到這樣一種不足的考核方式，我們可以嘗試在考核方式上做出一些調整.例如，我們可以把考核方式分為兩部分：理論考試和上機考查.對于理論考試部分，可適當增加一些開放型的簡答題，需要學生比較復變函數和數學分析中一些知識點的異同；對于實驗上機考查部分，主要考查學生利用已有的數學分析實驗基礎通過類比的方法解決一些與復變函數有關的實際問題.

4 結論

隨著計算機的飛速發展，傳統復變函數教學不能適應高校現代化教學，教學改革勢在必行.本文從教學改革和培養應用型人才的全局出發，結合自己多年教復變函數的經驗，探索了如何將類比思想融入到復變函數的整個教學過程的具體方法，認為把類比思想融入到復變函數教學的關鍵是分析推廣后出現的新情況和新問題及出現新問題的原因，剖析新概念與新理論的本質.力爭將類比思想與復變函數有關內容相結合，從而能夠培養學生感知事物存在特征與變化過程本質的能力、科學想象能力和科學推理能力，從而提高學生探討研究的能力.

[1]鐘玉泉.復變函數（第三版）[M].北京：高等教育出版社，2004.

[2]西安交通大學數學教研室編.復變函數（第四版）[M].北京：高等教育出版社，1996.

[3]陳紀修，於崇華，金路編.數學分析（第二版）[M].北京：高等教育出版社，2007.

[4]華東師范大學數學系編.數學分析[M].北京：高等教育出版社，2006.

[5]孫清華，孫昊.復變函數的內容、方法與技巧[M].武漢：華中科技大學出版社，2003.

[6]付愛玲.類比建構對復變函數教學的啟示[J].北京：中國科技信息，2010（18）：119.

The Research and Practice of Infiltrating the Idea of Analogy in Complex Analysis Teaching

LI Hong-guang
（College of Mathematics and Computer Science，Huaihua University，Huaihua，Hunan 418008）

Starting from the overall situation of teaching reform and training applied talents，combining with years of teaching experience of the author，the importance of infiltrating the idea of analogy in complex analysis teaching is presented firstly．And then，the specific plans of infiltrating the idea of analogy in the complex analysis teaching are discussed.The author hopes that it can be of some help in the teaching reform of complex analysis.

the idea of analogy；complex analysis；teaching reform

G642

A

1671－9743（2016）11－0088－02

2016-04-11

懷化學院教改項目（懷院發[2015]16號No.201527）.

李紅光，1979年生，男，湖南新寧人，講師，研究方向：函數論.