一種基于遺傳算法的TSP問題多策略優化求解方法

孫 文 彬，王 江

(中國礦業大學(北京)地球科學與測繪工程學院，北京 100083)

一種基于遺傳算法的TSP問題多策略優化求解方法

孫 文 彬，王 江

(中國礦業大學(北京)地球科學與測繪工程學院，北京 100083)

針對遺傳算法求解TSP問題解質量不高的缺陷，該文提出并設計了一種基于遺傳算法的多策略優化求解方法。首先，應用最鄰近法構建TSP的初始解；接著將路徑長度作為適應度評價指標，構建基于遺傳算法的TSP初始解優化方法，并根據試驗結果確定適合的遺傳算法參數；然后，針對遺傳算法易陷入局部最優的缺陷，借助去交叉和小角操作進一步優化TSP解路徑；在此基礎上，將遺傳算法進行并行化處理，通過增加遺傳算法的多樣性提高TSP解質量。最后，應用標準測試集(TSPLIB)進行試驗，結果表明：該算法能有效提高TSP解的質量，經并行遺傳算法、去交叉和小角優化后各測試數據集TSP解誤差率平均下降了22.57%；解的誤差率均在7.94%以內，質量明顯優于最鄰近法、插入法、2-Opt優化等傳統方法；在節點數多的測試數據集中算法也獲得了良好加速性能，8進程時算法加速比達2.51。

TSP問題;遺傳算法;優化策略;2-Opt

旅行商問題(Traveling Salesman Problem，TSP)是路徑規劃和組合優化領域中著名的NP- hard問題。車輛路徑規劃[1]、物流貨物配送[2]、飛機航線安排、災害應急調度[3]等問題均是典型的TSP問題[4-6]。目前，TSP求解算法主要分兩類：精確算法和近似算法。精確算法包括：群舉法、分支定界法、動態規劃法等。精確算法解的質量高，但求解所需時間長，無法用于大規模網絡TSP問題的求解。近似算法通過先產生初始解再優化的方式獲取TSP的解。生成初始解的主要方法有最近鄰法和插入法[7]；初始解優化多采用智能算法，主要方法有：貪心算法[8]、2-opt算法[9]、遺傳算法[10-16]、模擬退火算法[17]、蟻群算法[17-22]、免疫算法[23]等。Wang等在分析基于智能算法的TSP求解方法優缺點的基礎上[24,25]，指出遺傳算法受參數選擇和數據集分布結構的影響最小，陷入局部最優的概率最低。因此，本文設計了一種基于遺傳算法和多策略優化的TSP求解方法，以提高解的質量。

1 算法實現

大規模TSP問題的求解多采用求解速度快的近似算法，即首先生成初始解，再利用智能算法優化提高初始解的質量。遺傳算法求解速度快[25]，因此，將遺傳算法作為初始解優化的主要方法。為了避免遺傳算法出現過早收斂的情況，通過引入去交叉和小角操作盡可能降低遺傳算法收斂至局部最優的可能性，進而獲取到高質量的TSP解。

1.1 遺傳算法優化

遺傳算法通過遺傳變異操作將大量種群中具有不同結構形式的個體進行結構重組優化，進而不斷提取出個體中的較優結構，然后對它們進行下一步的尋優，最終逐漸逼近最優解。遺傳算法用于初始解優化時，將初始解路徑拆分為多個子路徑，每個子路徑作為獨立種群；將路徑長度作為適應度評價指標，通過種群間的交叉、變異來獲取更高質量的解。遺傳算法中初始種群規模、遺傳代數、交叉率、變異率等參數設定均會影響算法的優化效果。為此，本文應用TSPLib(http://www.iwr.uniheidelberg.de/groups/comopt/software/TSP LIB5/tsp/)中的3個標準測試數據(kroA200、u1060、pla7397)進行試驗，以確定最優的算法參數。

首先，保持遺傳代數、交叉率、變異率等參數不變,通過改變初始種群規模，分析初始種群規模對解質量的影響，并用誤差率評價TSP解的質量(如式(1)所示)。初始種群為500、 1 000、1 500、2 000、2 500、3 000時，測試數據集解的誤差率如表1所示。隨著初始種群數的增加，TSP解的誤差率下降了4%～10%；當初始種群數超過2 000時，TSP解的誤差率基本保持不變。同時，初始種群規模的擴大會導致算法求解時間增加，因此，綜合考慮上述因素將初始種群數確定為2 000。

誤差率(P)=(解—最優解)/最優解×100%

(1)

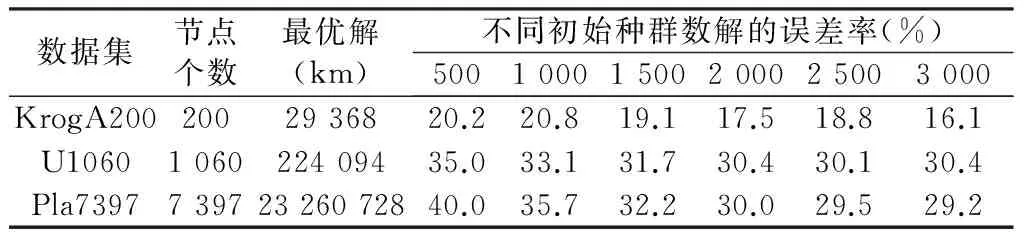
表1 初始種群數對解質量的影響

按照類似的方法，保持遺傳算法的其他參數不變，改變遺傳代數、交叉率、變異率等參數值，并計算TSP解的誤差率。遺傳代數為500、1 000、2 000、4 000、5 000時，解的誤差率如表2所示。交叉率為0.6、0.7、0.8和變異率為0.05、0.10、0.15時，TSP解的誤差率如表3所示。由表2可知，當遺傳代數達到4 000時，TSP解誤差率下降1.7%～8.8%；當交叉率為0.7，變異率為0.10時，TSP解的質量最佳。因此，將遺傳算法中的遺傳代數設定為4 000，交叉率設定為0.7，變異率確定為0.10。

表2 遺傳代數對解質量的影響

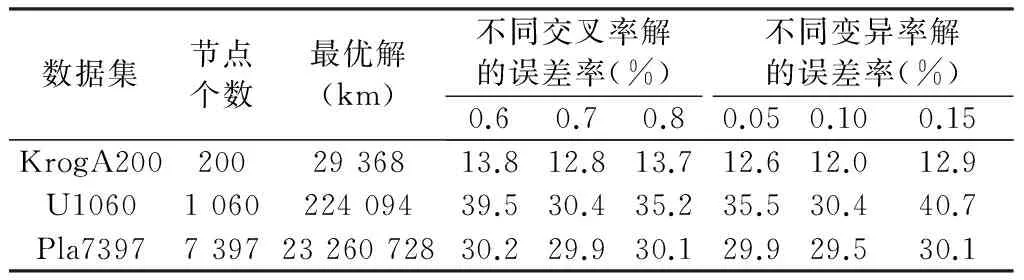
表3 交叉率和變異率對解質量的影響

1.2 去交叉和小角

由于遺傳算法會出現過早收斂的現象，易陷入局部最優，TSP解路徑中的交叉和小角現象是遺傳算法陷入局部最優的表現之一。為此，需要通過改變節點之間連接順序消除TSP解路徑中的交叉和小角現象，以避免遺傳算法出現過早陷入局部最優的問題。

交叉現象的探測可通過判斷解路徑中各線段是否相交來確定，若存在線段相交，則說明該TSP解中存在交叉現象。通過調整節點之間的連接順序可消除交叉問題，具體實現過程如下：假設子路徑(i,i+1)與(j+1,j+2)相交(如圖1a所示)，首先交換TSP解路徑序列中節點i+1和j+1的位置，然后將i+1到j+1的子路徑序列進行逆序排列，把原來的解{1,…，i-1,i,i+1,i+2…,j-1,j,j+1,…,n}轉變為{1,…，i-1,i,j+1,j,j-1…i+2,i+1,j+2，…，n}(如圖1b所示)，即可消除交叉現象。

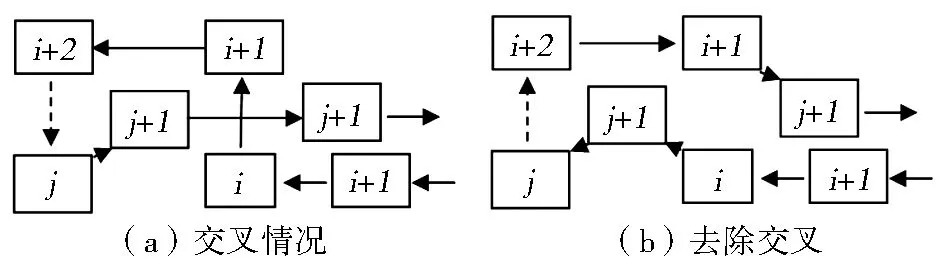
圖1 去交叉的實現原理

TSP解路徑中“小角”現象如圖2a所示。通過改變節點的連接方式能消除TSP路徑中的小角現象。TSP解是一個閉合回路，若要改變解路徑的連接方式，每次至少需要同時刪除和增加兩條邊。若要消除圖2a中節點i處的小角，則首先刪除連線(i-1,i)和(i+1,i+2,)，增加連線(i-1,i+1)和(i,i+2)，改變節點i和i+1的連線方向。若刪除兩條邊的長度之和大于增加兩條邊的和，即D(i-1,i)+D(i+1,i+2)>D(i-1,i+1)+D(i,i+2)(D(i,i+1)為節點i到i+1的距離)，則能提高TSP解的質量。重復上述的過程，直至任意相鄰3個節點間不存在小角為止。

圖2 鄰近置換示意

1.3 算法的并行化

增加遺傳算法的多樣性能提高算法求解的精度。而并行算法能利用多機多核的計算資源運行多個遺傳算法，可增加算法的隨機多樣性，進而既可提高遺傳算法的優化效果,又能加快算法的收斂速度。為此，本文將遺傳算法進行了并行化，即在TSP求解過程中，利用多機多核的計算資源分別開辟多個進程，運行多個遺傳算法優化TSP的初始解；從各進程優化結果中取出最優的解，再進行去交叉和小角；重復上述過程，直到TSP優化結果滿足設定的退出條件為止。這樣既可提高TSP解的質量，又能加快遺傳算法收斂速度，提高TSP求解速度。

2 試驗分析

為了驗證算法的正確性和有效性，本文應用標準測試數據集TSPLIB進行相關試驗。以MPI并行編程模型和GDAL地理數據操作開源庫為基礎，利用2臺4核計算機搭建Windows集群系統，具體配置如下：CPU的型號為I5-2380P，主頻為3.40 GHz，內存大小為8 G。

試驗首先分析了遺傳算法、去交叉和小角對初始解的優化效果(表4)。采用最鄰近法生成初始解的誤差率在20.57%～31.01%之間；利用遺傳算法優化初始解后，各測試數據集解誤差率在5.24%～15.43%之間，解誤差率平均下降了16.8%；再經去交叉和小角處理后，TSP解誤差率平均又下降了5.77%。由此可見，采用并行遺傳算法、去交叉和小角多種優化策略能極大程度提高初始解的質量，使初始解的誤差率平均下降22.57%。

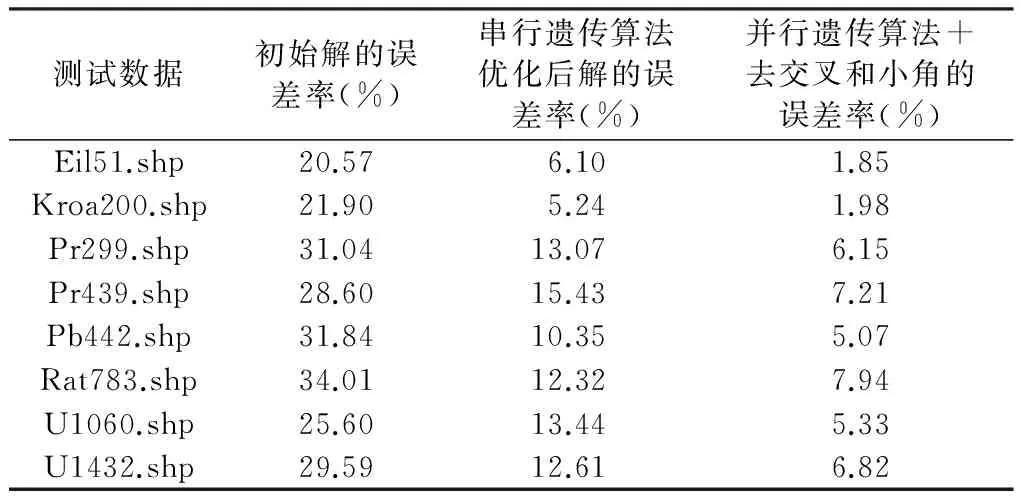
表4 遺傳算法、去交叉和小角的優化效果

試驗還對比分析了本文算法與最鄰近法、插入法、最鄰近和插入混合方法、2-Opt解的質量。最鄰近法、插入法、最鄰近和插入混合法的試驗數據來源于參考文獻[7]。在試驗中，應用上述算法進行10次TSP問題的求解，分別統計出各測試數據集的最優解值，結果如表5所示。由表5可知，本文算法的最優解誤差率在1.85%～7.94%之間(各數據集解的最優解誤差率如圖3所示),算法解的質量明顯高于最鄰近法、插入法、最鄰近和插入混合法、2-Opt法。

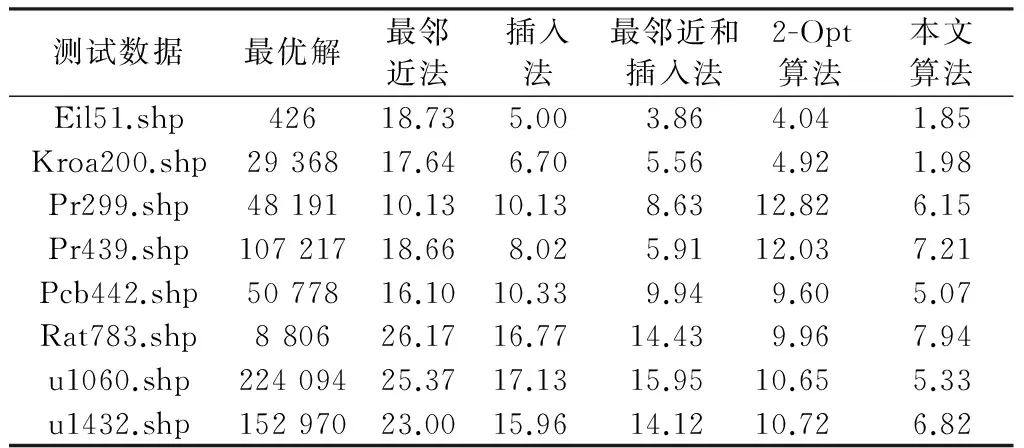
表5 不同算法最優解誤差率的對比

此外，本文測試了不同數據集并行優化算法的加速比情況(表6)。當測試數據集節點數較少時，并行算法由于增加了不同進程間的通訊時間，通訊消耗時間抵消了多進程計算節省的時間，算法加速效果不理想，甚至出現并行算法計算時間多于串行算法的現象。隨著測試數據集節點數的增加，并行算法獲得良好的加速性能，測試數據集Pla 7379在8進程時，加速比達到2.51。

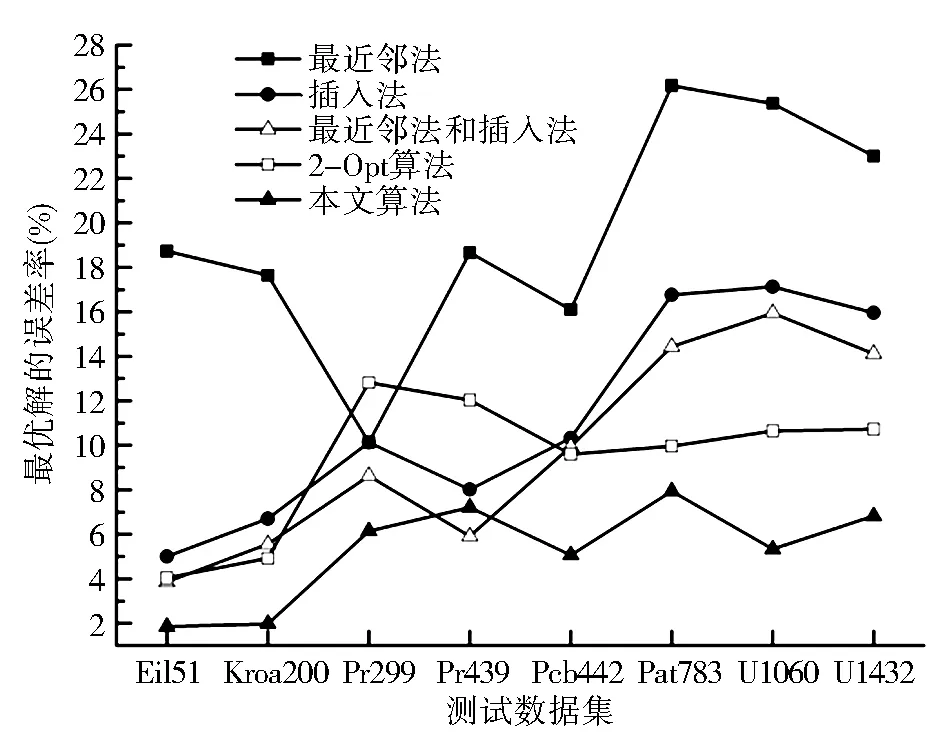
圖3 最優解的誤差率

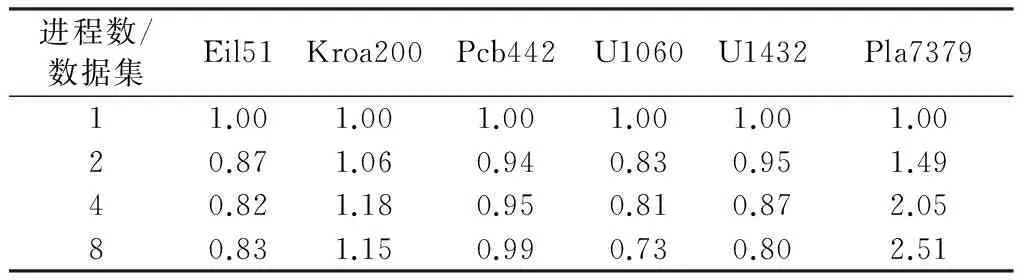
表6 不同測試數據集加速比情況

3 結論

本文設計了一種基于遺傳算法與多策略優化的TSP求解方法，應用標準測試數據集進行了相關試驗。結果表明：經遺傳算法、去相交和小角、并行化等多策略優化措施處理，TSP解的質量得到大幅提高，各測試數據集最優解的誤差率均在7.94%以內；本文算法求取TSP解的質量明顯優于最鄰近法、插入法、2-Opt優化等傳統方法；在節點數多的測試數據集中，算法也獲得了良好的加速性能，8進程算法加速比均在2.5以上。由于本文采用算法并行的策略實現了遺傳算法的并行化，這導致大多數測試數據集并行加速效果不理想。若要進一步提高算法的并行效率，需設計細粒度并行模式，即將遺傳算法中交叉變異過程進行并行化，進而獲得良好的加速比。此外，本文算法僅應用TSPLIB中的部分測試集進行了試驗，無法保證算法適用于所有的標準測試集，因此，需應用更多的測試數據集進行試驗，分析本文算法的普適性。

[1] 唐健,史文中,孟令奎.基于遺傳算法的時相關動態車輛路徑規劃模型[J].武漢大學學報(信息科學版),2008,33(8):875-879.

[2] 李清泉,張金亭,黃經南.一個物流配送優化算法[J].武漢大學學報(信息科學版),2003,28(1):9-13.

[3] 孟永昌,楊賽霓,史培軍.基于改進遺傳算法的路網應急疏散多目標優化[J].武漢大學學報(信息科學版),2014,39(2):201-205.

[4] 尹大胐,方裕.疏散規劃的一種優化算法[J].地理與地理信息科學,2014,29(2):31-35.

[5] 胡勇,宗真,羅文,等.多條件約束應急疏散路徑分析的幾何代數方法[J].地理與地理信息科學,2012,28(5):47-5.

[6] 方金云,張聰,邱強,等.一種基于網絡數據的LRP并行求解算法[J].地理與地理信息科學,2013,29(4):13-16.

[7] 饒衛振,金淳，黃英藝.求解TSP問題的最近領域與插入混合算法[J].系統工程理論與實踐,2011,31(8):1419-1428.

[8] 于瑩瑩,陳燕,李桃迎.改進的遺傳算法求解旅行商問題[J].控制與決策,2014,29(3):1-6.

[9] 劉荷花,崔超,陳晶.一種改進的遺傳算法求解旅行商問題[J].北京理工大學學報,2013,33(4):390-393.

[10] 鄧長春,朱儒明,李詠霞,等.一種求解TSP問題的多種群并行遺傳算法[J].計算機仿真,2008,25(9):187-190.

[11] 趙宏立，龐小紅，吳智銘.基因塊編碼的并行遺傳算法及其在TSP中的應用[J].上海交通大學學報,2004,38(增刊):213-217.

[12] 許智宏,宋勃,郭艷艷.模擬退火與蟻群混合并行算法解旅行商問題[J].河北工業大學學報,2010,39(2):48-51.

[13] 戚玉濤,焦李成,劉芳.基于并行人工免疫算法的大規模TSP問題求解[J].電子學報,2008,36(8):1552-1558.

[14] 唐立新.旅行商問題(TSP)的改進遺傳算法[J].東北大學學報(自然科學版),1999,20(1):40-42.

[15] 謝旻.一種混合例子群優化算法在TSP中的應用[J].太原理工大學學報,2013,44(4):506-509.

[16] 杜鵬楨,唐振民,孫研.一種面向對象的多角色蟻群算法及其TSP問題求解[J].控制與決策,2014,29(10):1729-1736.

[17] 楊華芬,魏延.一種求解TSP問題的改進遺傳算法[J].重慶工學院學報(自然科學版),2007,21(5):86-90.

[18] BAI J,YANG G,CHEN Y,HU L,et al.A model induced max-min ant colony optimization for asymmetric traveling salesman problem[J].Applied Soft Computing,2013,13:1365-1375.

[19] ZHU Q,CHEN S.A new ant evolution algorithm to resolve TSP problem[C].Sixth International Conference on Machine Learning and Application(ICMLA 2007),2007.62-66.

[20] ANURAJ M,REMYA G.A parallel implementation of ant colony optimization for TSP based on MapReduce framework[J].International Journal of Computer Application,2014,88(8):8875-8887.

[21] PAN G,LI K,OUYANG A.Hybrid immune algorithm based on greedy algorithm and delete-cross operator for solving TSP[J].Soft Computer,2016,20:555-566.

[22] WANG H.Comparison of several intelligent algorithms for solving TSP problem in industrial engineering[C].The 2nd International Conference on Complexity Science & Information Engineering,2012.226-235.

[23] GU J.Efficient local search with search space smoothing:A case study of the traveling salesman problem (TSP)[J].IEEE Transactions on Systems,Man,and Cybernetics,1994,24(5):728-735.

[24] WANG J,ERSOY O,HE M,et al.Multi-offspring genetic algorithm and its application to the traveling salesman problem[J].Applied Soft Computing,2016,43:415-423.

[25] TOBIAS M,OLA S.Removing and adding edges for the traveling salesman problem[J].Journal of the ACM,2016,63(1):2-29.

An Algorithm for TSP Problem Based on Genetic Algorithm and Multi-optimization Operation

SUN Wen-bin,WANG Jiang

(SchoolofGeo-scienceandSurveyingEngineer,ChinaUniversityofMining&Technology(Beijing),Beijing100083,China)

To overcome the deficiency of poor quality of TSP path by using genetic algorithm,an algorithm based on genetic algorithm and multi-optimization operation is presented.Firstly,initial TSP path is approached by using the nearest neighbor method;then,the length of TSP path is considered as the fitness evaluation index and the optimizing method of TSP initial solution based on genetic algorithm is described.According to the experiment results,the suited genetic algorithm parameter can be determined.Next,pointing to the shortcoming that genetic algorithm is easy to fall into local optimum,to use the cross-removing and small-angle operation optimize the solution path of TSP;on this basis,the genetic parallel algorithm,and increasing the diversity of algorithm can improve the quality of TSP solution.Finally,the experiment is done by using the standard test datasets(TSPLIB).The results show that:this algorithm can effectively improve the quality of TSP solution,after parallel genetic algorithm,cross-removing and small-angle optimization,the TSP solution error rate of every test data set decreases by 22.57 percent on average;the error rate of the solution is within 7.94 percent,obviously better than the nearest neighboring method,inserting method,2-Opt optimization and other traditional methods;among the testing datasets that have many nodes,the algorithm also obtains a good acceleration performance and algorithm acceleration rates are more than 2.51 when it is 8-processes.

Traveling Salesman Problem(TSP);genetic algorithm;optimization strategy;2-Optimization(2-Opt)

2015-12-10；

2016-03-29

國家自然科學基金資助項目(41201416)

孫文彬(1977-)，男，博士，副教授，從事全球離散格網、智能計算、并行計算等方面的研究。E-mail:swb1996@126.com

10.3969/j.issn.1672-0504.2016.04.001

P208；TP301.6

A

1672-0504(2016)04-0001-04