2.5D結構筒狀立體機織物細觀分析及建模
邵明正
(天津工業大學復合材料研究所,天津 300387)
2.5D結構筒狀立體機織物細觀分析及建模
邵明正
(天津工業大學復合材料研究所,天津 300387)
文章為了探究2.5D結構筒狀立體機織物的細觀幾何關系,通過顯微觀察和結構分析,提出緯紗截面為雙凸透鏡截面、經紗截面為扇形截面的假設,并建立了2.5D結構筒狀立體機織物實體模型和2.5D結構細觀幾何結構模型,推導了細觀幾何表達式和細觀微元中纖維體積分數計算公式。結果表明2.5D結構被用于筒狀織物時,細觀幾何結構會發生一些改變。
筒狀立體機織物;2.5D結構;細觀幾何模型。
1 前言
筒狀復合材料結構件是在工程中常用的基本構件,使用筒狀織物作為增強體,若采用高性能纖維(如碳纖維、芳綸纖維)進行增強體織造,則使構件具有輕質、高比強、耐疲勞、耐腐蝕等優越性能。目前,筒狀復合材料構件已用于生產結構支架、輸送管道、襯套、罩體、超耐高溫隔熱管等產品,在航空航天、化學化工、能源輸送、醫學等多個領域應用前景廣闊[1~2]。
筒狀立體機織物是管狀織物與三維機織技術的有機結合,立體機織結構克服了層間強度低、剪切強度差、易分層等缺陷,具有結構的多樣性、形態的可設計性、性能的綜合性等優點。2.5D結構是筒狀織物中常見的結構,其雖早已廣泛應用到工程實踐中,但針對2.5D結構筒狀織物細觀幾何關系描述的文獻很少。很多人認為2.5D結構筒狀織物僅僅是把2.5D結構平移到圓形模具上,與普通2.5D結構織物并無差異,這種觀點是不科學的。2.5D結構筒狀織物具有不同于普通2.5D結構織物的幾何形態,這種差異會對細觀幾何結構產生一定影響。
為了對織物細觀結構進行更準確描述,國內外很多學者對織物截面提出過很多假設。20世紀30年代,Pierce提出了圓形截面假設[3]。后來Dickson[4]與Kemp[5]在Pierce的模型基礎上做了修正,并提出跑道形截面的假設,并討論了織物在緊密排列時的結構狀態。Byun和Chou[6]采用了凸透鏡截面假設,并建立了經紗壓縮現象的關系式。Naik等[7]研究了織物結構的橢圓截面假設,對于筒狀立體機織物紗線,還有很多不同的紗線截面假設。焦志文、周儲偉等[8]假設緯紗正六邊形截面,經紗為扇形截面,研究了圓管狀立體機織復合材料的力學性能。陳陽[9]把跑道形紗線截面簡化了為內切八邊形截面,并對三維機織圓管單胞模型進行有限元分析。劉佳、周光明等[10]假設了三維機織管狀復合材料經緯紗為橢圓截面,建立力學模型預測其工程彈性常數。這些紗線截面假設不斷提出,使織物細觀描述越來越接近織物真實情況,推動了織物建模研究的深入和織物性能研究水平的提高。
運用有限元模擬的方法對結構件性能進行評價,已成為復合材料結構設計過程中必不可少的一環。很多研究人員利用有限元分析方法對2.5D結構進行分析評價[11~13],其中最關鍵部分就是建立接近織物結構的實體模型,筒狀結構件作為最常見的構件類型,準確進行筒狀織物建模非常必要。
2 2.5D筒狀立體織物
筒狀立體機織物是管狀復合材料的增強體,是構件承載的關鍵。本文中筒狀織物的織物結構為2.5D結構,又稱角聯鎖結構。2.5D結構是三維機織物組織中的一個重要分支,由接結經紗(或接結緯紗)、緯紗(或經紗)、襯經(填充經紗)和襯緯(填充緯紗)等紗線系統組成,前兩個系統是構成三維機角聯鎖結構所必需的紗線,其他兩個系統可以自由選擇[14]。
2.5D結構具有穿過厚度方向的接結紗, 具有較高層間剪切強度、抗沖擊損傷性、高比強度和高比模量,同時具有耐腐蝕、抗高溫等優點,通過有效的組織結構設計,可以提高纖維、紗線對織物綜合性能的貢獻率。
筒狀立體機織物2.5D結構進行立體織造,經紗排紗圖如圖1所示,由排紗圖可以看出2.5D結構筒狀立體織物,經紗列數一定。經紗層每層的紗線數目相同,而經紗層內接圓由內而外不斷增大,所以每層經紗的延展情況不同,即經紗層的厚度也不一樣。

圖1 經紗排紗圖
3 2.5D結構筒狀立體機織物細觀結構
3.1 紗線截面
3.1.1 紗線截面假設
紗線截面形狀的影響因素復雜,纖維的材料特性、紗線參數,織物的組織結構等都會對紗線截面產生影響。從紗線受力的角度分析,紗線的截面形狀主要是受周圍紗線擠壓力的綜合作用,而呈現不同的形狀。

圖2 經緯紗擠壓作用示意圖
如圖2所示,F11使紗線保持順直和集束,F22使紗線壓縮變形,共同作用的結果使紗線截面呈扁平化。
如圖3所示,緯紗受相鄰上下經紗擠壓作用兩走向相反的經紗形成類雙凸透鏡邊界。從圖4緯紗顯微鏡照片觀察到緯紗截面近似為雙凸透鏡,故本文將緯紗截面假設成雙凸透鏡形狀截面,如圖5。

圖3 經緯紗交織實體截面圖

圖4 緯紗截面顯微鏡照片

圖5 緯紗截面圖
經紗受上下緯紗擠壓作用,又因為整個織物截面為圓形,經紗層與緯紗層相間分布,每層經紗成環形,故假設經紗截面為扇形,見圖6、圖7。

圖6 經紗截面圖

圖7 經緯紗交織實體截面圖
經紗層厚度:H=R1-R2
為了更好地建立幾何模型,對于2.5D筒狀立體織物的織物狀態和內部結構,進行一些適當的簡化假設,假設如下:
(1)織物結構均一,緯紗沿軸向排列,經紗沿圓周方向排列,經緯紗規則、緊密,紗線截面積保持不變。
(2)緯紗截面為雙凸透鏡形,經紗截面為扇形,相鄰經紗之間無間隙,經緯紗表面相切。
(3)緯紗路徑為圓形,經紗路徑由直線段與弧線段組成,弧線部分與直線部分相切。
3.1.2 變截面經紗
根據對織物幾何模型的假設,建立經紗和緯紗的實體模型,如圖8、圖9所示。經紗接結上下相鄰兩層緯紗(圖10),由于兩層經紗的厚度不同,所以經紗扇形截面是變化的(圖8)。扇形截面的內徑R1、外徑R2及厚度H的取值已在之前討論過,經紗路徑由直線段與圓弧構成。

圖8 變截面經紗實體模型

圖9 緯紗實體模型
如圖9所示,緯紗實體截面為雙凸透鏡形,紗線路徑為圓形。經紗與緯紗實體模型按照截面參數建立,裝配組成織物的實體模型,如圖10所示。

圖10 筒狀織物單根經紗實體模型圖
3.2 織物厚度確定
由于經紗層每層經紗的延展程度不一樣,經紗層厚度由內及外逐漸減小,所以經紗厚度須由芯模外徑向外依次求出,才能求出最終織物厚度。求解步驟如下:
(1)已知經紗列數n,經紗截面S紗,芯模外徑 R0。
(2)經紗層厚度為H=R1-R2,通過πR22=πR12+nS紗,求得R2。其中 R1為經紗層內圓,R2為經紗層外圓。第一層經紗R1內徑為芯模外半徑R0。
(3)下一周經紗層內圓R1′=R2+2B,其中2B為緯紗層厚度,重復步驟(2),直至最后一層經紗。
3.3 細觀幾何結構分析
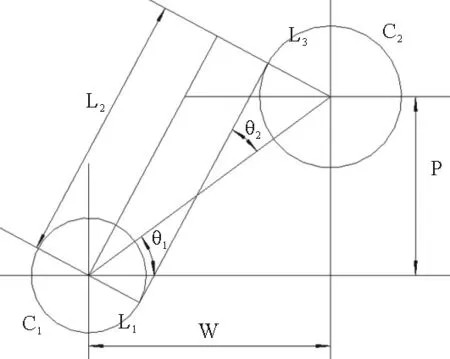
取織物的一個細觀幾何結構進行分析,如圖11所示。H1、H2是相鄰的兩層經紗層厚度,經紗層厚度 H2 圖11 細觀幾何結構示意圖 雙凸透鏡形狀由兩圓相交而成,作輔助圓C1、圓C2。直線段部分傾角為θ=θ1+θ2。 圖12 幾何輔助求解圖 由幾何關系可得:兩圓之間位置參數W、P的值:W=aP=b-2R+2B 直線段L1:L1=R1(θ1+θ2) 圓弧L3弧長為:L3=R2(θ1+θ2) 經紗長:L=L1+L2+L3 3.4 微元體積含量計算 如圖13所示,選取長為2a,高為b,寬為2c的六面體微元,一個微元共4根經紗段,2根緯紗段。 圖13 微元實體圖 式中:Sj與Sw分別為經緯紗截面面積 微元內纖維體積分Vf:Vf=Vj+Vw 根據緯紗雙凸透鏡截面,經紗扇形變截面假設,繪制了2.5D結構筒狀立體織物三維實體模型(見圖14 )和2.5D結構筒狀立體機織物巨元體實體圖(見圖15)。 圖14 2.5D結構筒狀立體織物實體模型圖 圖15 筒狀織物巨元體實體圖 本文基于2.5D結構筒狀立體機織物顯微觀察和結構分析,假設雙凸透鏡緯紗截面以及扇形經紗截面,分析了將2.5D結構運用到筒狀織物織造時所產生的細觀幾何差別,尤其是經紗截面形狀趨于扇形截面,環形經紗層厚度由內及外不斷減小的情況。分析結果表明2.5D結構筒狀立體機織物不完全等同于2.5D結構立體織物,具有特殊結構特征。 為了描述細觀結構,對織物結構進行了一些理想化假設。基于雙凸透鏡緯紗和扇形經紗,推導了2.5D的細觀幾何表達式和細觀微元中纖維體積分數計算公式。總結了經紗層變厚度時,筒狀織物厚度的求解方法,并繪制了2.5D結構筒狀立體機織物三維整體模型。 雖然2.5D結構已經在實際生產中得到運用,但是對于不同形狀進行近凈成形時,織物結構會產生一些相應的變化,不應一律當成固定結構處理。在使用有限元方法對構件進行模擬分析時,更應關注所建織物模型的準確性,這樣才能得到更準確的模擬結果。 [1] 車劍飛,黃潔雯,楊娟.復合材料及其工程應用[M].北京:機械工業出版社,2006. [2] 張曉明,劉雄亞.纖維增強熱塑性復合材料及其應用[M].北京:化學工業出版社,2006. [3] Pierce F T. The Geometry of Cloth Structure[J].Journal of the Textile Institute,1937, 28(2):45—96. [4] Dickson J. Practical Loom Experience on Weavablity Limits[J].Textile Research Journal, 1954,24(12):1083—1093. [5] Kemp A. An Extension of Peirce's Cloth Geometry to the Treatment of Non-circular Threads [J].Journal of the Textile Institute,1958,49(1):44—48. [6] Byun J H,Chou T W. Elastic Properties of Three-dimensional Angle-interlock Fabric Preforms [J].Journal of the Textile Institute,1990,81(4):538—548. [7] Naik N K Kuchibhotla R.Analytical Study of Strength and Failure Behaviour of Plain Weave Fabric Composites Made of Twisted Yarns[J].Composite Part A Applied Science and Manufacturing 2002,33(5):697—708. [8] 焦志文,周儲偉.圓管狀立體機織復合材料的多尺度分析[J].復合材料學報,2010,(5):122—128. [9] 陳陽.圓織立體碳纖維復合材料三角架的強度分析[D].上海:東華大學,2014. [10] 劉佳,周光明,王新峰,等.三維機織管狀復合材料力學模型與實驗驗證[J].南京航空航天大學學報,2004,36(4):444—448. [11] 姚瑤,金利民.層層接結三維角聯鎖機織復合材料的三點彎曲疲勞破壞[J].纖維復合材料,2014(2): 41—44. [12] 王春霞,宋孝浜,金利民.三維角聯鎖機織復合材料三點彎曲破壞的有限元計算[J].紡織學報,2014(3):41—45. [13] 陳凡軍,羅軍,陳革.三維角聯鎖機織復合材料有限元分析[J].東華大學學報(自然科學版),2015(1):28—31. [14] 郭興峰.三維機織物[M].北京:中國紡織出版社,2015. 聲 明:為適應我國信息化建設需要,擴大作者學術交流渠道,本刊已加入《中國學術期刊(光盤版)》、《中國萬方數字化期刊群》、《中文科技數據庫》、《中教數據庫》和超星“域出版”平臺。作者文章著作權使用費與本刊稿酬一次性給付(已在收取發表費時折減和換算為雜志贈閱)。如作者不同意將文章編入上述數據庫,請在來稿時聲明,本刊將做適當處理。 Meso-analysis and Modeling of Tubular Woven Fabric with 2.5D Structure ShaoMingzheng (Institute of Composite Materials of Tianjin Polytechnic University,Tianjin 300387, China) In order to explore the meso-geometry of the tubular woven fabric with 2.5D structure, lenticular cross section of weft and sector cross section of warp were assumed by means of the micrograph observation and analysis of fabric structure. The solid model of 2.5D structure tubular woven fabric and the meso-geometry model with 2.5D structure and was established. Meso geometric expression and calculation formula of fiber volume fraction in a micro-unit was also derived. The results show that when the 2.5D structure is used in the tubular fabric, some changes have occurred in the meso-geometry structure. tubular woven fabric; 2.5D structure; meso-geometry model 2016-11-10 邵明正(1989—),男,山東臨沂人,碩士研究生。 TS105.1+13 A 1009-3028(2016)06-0041-05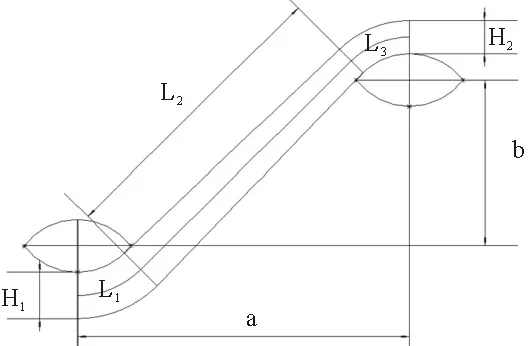








4 結語

