生絲線密度檢驗精密度的評價與測定

許建梅， 周 穎， 李 淳， 伍冬平， 白 倫

(1. 蘇州大學 紡織與服裝工程學院， 江蘇 蘇州 215021； 2. 現代絲綢國家工程實驗室， 江蘇 蘇州 215123；3. 浙江絲綢科技有限公司， 浙江 杭州 310011； 4. 廣東出入境檢驗檢疫局， 廣東 廣州 510623)

生絲線密度檢驗精密度的評價與測定

許建梅1，2， 周 穎3， 李 淳4， 伍冬平3， 白 倫1

(1. 蘇州大學 紡織與服裝工程學院， 江蘇 蘇州 215021； 2. 現代絲綢國家工程實驗室， 江蘇 蘇州 215123；3. 浙江絲綢科技有限公司， 浙江 杭州 310011； 4. 廣東出入境檢驗檢疫局， 廣東 廣州 510623)

為準確評價采用生絲線密度儀進行線密度檢驗的精密度(即重復性與重現性誤差)，掌握樣本的非均質性對檢驗結果精密度的影響程度，利用抽樣數量為200絞100回(112.5 m)時不同規格生絲線密度檢驗的精密度數據，設計了2種試驗方案進行精密度的測定。一是采用同一樣本進行5個實驗室間的循環比對試驗；二是由5個實驗室分別對同一批絲的不同樣本進行檢驗。試驗結果表明，采用同一樣本進行檢驗時精密度水平很高，重復性與重現性平均誤差變異小于3%，而采用不同樣本時，平均誤差變異達到了10%左右，表明生絲樣本的非均質性對生絲線密度檢驗精密度的影響較大，應用該試驗方法進行精密度評價和測定時應考慮樣本的非均質性，以便真實地反映實際檢驗的精密度水平。

生絲； 線密度檢驗； 精密度； 非均質性； 抽樣數量

由于繭絲由粗到細再到粗的固有的線密度(俗稱為纖度)變化狀態，再加上繭絲原料莊口與莊口間，甚至同一莊口內繭絲線密度的較大差異，導致所繅制的生絲線密度波動相對較大。這使得同一批絲的生絲線密度的波動性檢驗從其進入流通領域開始就一直成為一項非常重要的檢驗項目。對于它的研究最早在19世紀60年代，文獻[1]報道過生絲線密度不勻率的測定方法。提出在對4～5根繭絲繅成的生絲的線密度進行測定時，樣本數量采用6絞小絞絲，如果線密度最大差不超過2.2～3.3 dtex，則認為該生絲是均勻的。1915年美國絲綢協會開始組織人員專門研究生絲檢驗分級問題，并于1921年提出生絲分級報告，在該報告中采用了通過測量30絞400回(每絞長度400回，100回=112.5 m)小絞絲的平均線密度,以及60絞200回小絞絲的平均線密度與線密度開差(最大值與最小值之差)來衡量生絲線密度及其不勻率質量[2]。1928年在橫浜召開的第1次美日生絲分級技術會議上，日本提出線密度檢驗的樣本容量應改為200絞小絞絲，并改為用線密度平均偏差替代線密度開差。該提議雖然未能在會上通過，但是在隨后幾年的標準修訂中逐步被采納。1950年國際絲綢協會發布的國際生絲檢驗標準基本是以日本標準為參照。1955年在比利時召開的第5次國際絲協大會上，生絲線密度偏差的計算方法由平均偏差改為均方差[1]。到19世紀末期，日本由最大的生絲生產出口國逐漸轉變為生絲消費國，而中國成為世界最大的生絲出口國[3]。對于生絲線密度檢驗方法的研究也取得新的進展，分析了100回檢驗絲長與400回檢驗絲長的差異[4]。近幾年，中國生絲采用電子檢測技術有了較大的發展，也有不少關于采用生絲電子檢測設備檢測生絲線密度變異的研究[5-7]，但是對于長片段生絲線密度不勻以及線密度分布的給出，生絲電子檢測手段仍然沒有辦法解決。為此，一直以來國際絲綢貿易中仍然采用生絲線密度儀或者電子天平稱量來進行生絲線密度檢驗。

在世界范圍內，生絲線密度檢驗中最突出的問題就是，不同國家的線密度檢驗標準在抽樣長度和抽樣數量上仍然存在較大差異。如印度2007年最新修訂的IS1 5090《生絲分級與測試方法》標準中規定的生絲線密度檢驗樣本量為36.7 dtex及以下的生絲采用40絞400回小絞絲，37.8 dtex及以上的生絲采用80絞100回小絞絲；而日本則是400絞100回小絞絲[8]，中國則是200絞100回小絞絲[9]。這樣的差異就給國際生絲貿易帶來了諸多不便，甚至引起反傾銷申訴[10-11]。中國因為同一批絲在不同的檢驗體系里所得到的線密度偏差數值相差較大，使得同一指標無法采用統一的尺度進行質量評價。世界絲綢界急需建立一個統一的生絲線密度質量檢驗體系，即可供世界各生絲采購商與生產商參照的國際標準體系。為此，本文研究通過在一定檢驗方法與抽樣數量下的生絲線密度檢驗的精密度進行評價與測定，分析生絲的非均質性對精密度水平的影響，以期為生絲線密度檢驗的國際標準化研究提供實驗數據與理論參考。

1 精密度計算方法

任何一種測量方法在制定成標準推廣使用時，都需要對其測量方法進行精密度試驗，并給出精密度試驗結果，使得使用該方法標準的用戶能夠正確估計測量值的準確度。根據ISO 5725-1：1994《測量方法和結果的準確度(正確度與精密度)—第1部分：一般原理和意義》中的規定，精密度是指在規定的條件下，各獨立測試結果之間的一致性程度，通常用測量結果的標準差或標準差變異來表示。這里的規定條件指重復性條件和再現性條件這2種極端情況。

根據ISO 5725-1：1994中的定義，為實現重復性條件，試驗需在同一個實驗室內的同一臺設備上進行，并且需由同一操作人員按相同的測試方法，在盡可能短的時間內對同一被測對象進行多次重復測量，每次測量相互獨立。在滿足重復性條件下測得的各獨立測量結果的標準差及標準差變異則反映了該測試方法的重復性。而再現性試驗則是在不同的實驗室進行的，試驗由不同的操作員按照同一試驗方法，使用不同的設備，對同一被測對象進行相互獨立測試。在此條件下測得的各獨立測量結果的標準差或標準差變異則反映了該測試方法在不同的實驗室間使用時試驗結果的再現性。

在設計試驗時往往重復性與再現性測試是同時進行的。在進行生絲線密度偏差與最大偏差的精密度試驗時，設p為參與的實驗室數量，n為試驗樣品在每個實驗室的重復測量次數，則第i個實驗室對某樣品進行的第j次檢測值可表示為xij(i=1,2,…,p;j=1,2,…,n)。由此可以計算得到該樣品在每個實驗室測得的平均值

(1)

以及該樣品所有測量值的平均值

(2)

利用式(2)，則可以計算得到每個實驗室的測量結果的方差，即各個實驗室內方差

由以上各個實驗室內方差，即可算得重復性標準差

(3)

此外，由測量數據還可得到實驗室間方差

(4)

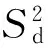
(5)

根據ISO5725-2：1994《測量方法和結果的準確度(正確度與精密度)—第2部分：確定標準測量方法重復性與再現性的基本方法》，由式(3)和式(5)可以得到再現性標準差

(6)

2 試驗方案的設計

測試方法的精密度試驗目的是得到該測試方法的重復性與再現性結果，從而為以后單個測試的準確度提供參考，但是生絲線密度檢驗有其特殊性，那就是生絲屬于非均質物料。同一批生絲的線密度質量差異比較大，即使采用較大的樣本量(涉及到檢測費用、樣品費用，無法無限度地提高樣本容量)以及盡可能的隨機抽取方式仍然不能保證樣品的均一性，并且樣本的差異性已經成為生絲線密度檢驗中影響正確度與精密度產生的主要原因。在這種情況下，各實驗室間采用相同樣本所得到的精密度對實際生絲線密度抽樣檢驗所起到的參考并不大，有時反而會產生誤導。

為了能夠正確反映實際生絲線密度檢驗的精密度，并分析生絲的非均質性對試驗精密度的影響程度，設計了2種試驗方案。一種是采用同一樣本進行5個實驗室的循環試驗，這里簡稱為循環試驗方案，該試驗方案反映的是可能由于室驗室環境、設備、操作人員不同引起的試驗精密度誤差；另一種是從同一批絲中按照同樣的取樣方法分別抽取5個等效樣本，分送5個實驗室進行檢測，簡稱抽樣方法試驗方案，該試驗方案反映的是可能由于樣本不同，室驗室環境、設備、操作人員不同引起的試驗精密度誤差。

2種方案均對A(名義線密度為23.3 dtex)、B(名義線密度為23.3 dtex)、C(名義線密度為31.1 dtex)、D(名義線密度為46.6 dtex)這4個批次的生絲進行試驗。2種方法的抽樣方法均按GB/T 1798—2008《生絲試驗方法》中的規定進行，每批生絲僅抽1組樣本，每組樣本均為200絞100回。

第1種方案中，4批生絲的樣本均先送到實驗室1進行測試，每個樣品在每個實驗室的重復測量次數均為3次。實驗室1測完后立即將樣本遞送給實驗室2進行檢測，該循環試驗按照：實驗室1→實驗室2→實驗室3→實驗室4→實驗室5的順序依次進行樣品傳遞與檢測。

第2種方案中，試驗對象仍然是這4批生絲，即A、B、C、D。每批生絲按GB/T 1798—2008規定進行抽樣，每組樣本均為200絞100回，每批生絲抽取5組樣本，然后分別寄往5個實驗室。

3 試驗結果與分析

3.1 原始檢測數據

根據以上試驗方案，共測得4組數據，分別為2種方案下4批絲由5個實驗室檢測得到的線密度偏差與最大偏差數據，見圖1、2。

從圖1、2可看出：每個實驗室進行的3次重復試驗檢測結果差異較小；在循環試驗中各實驗室間的檢測值差異不大，但是在抽樣方法試驗中各實驗室間的檢測值差異明顯增大，重現性誤差增大。具體的精密度數據還需要進行計算。

3.2 精密度計算

分別根據式(3)和式(6)可計算得到2種測試方案下的試驗精密度，結果見表1、2。表1示出循環試驗方案中線密度檢驗的精密度，即重復性與重現性均方差以及變異。從表中可看出，在循環試驗中采用同一測試樣，實驗室內與試驗間的重現性與重復性相當高，試驗結果的差異性大多在5%以下，重現性與重復性平均值僅為1.99%和2.63%。

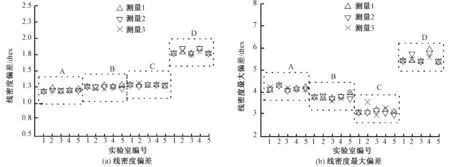
圖1 各批次生絲在各實驗室的檢測數據(循環試驗)

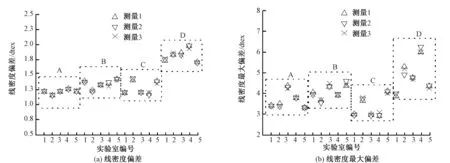
圖2 各批次生絲在各實驗室的檢測數據(抽樣方法試驗)

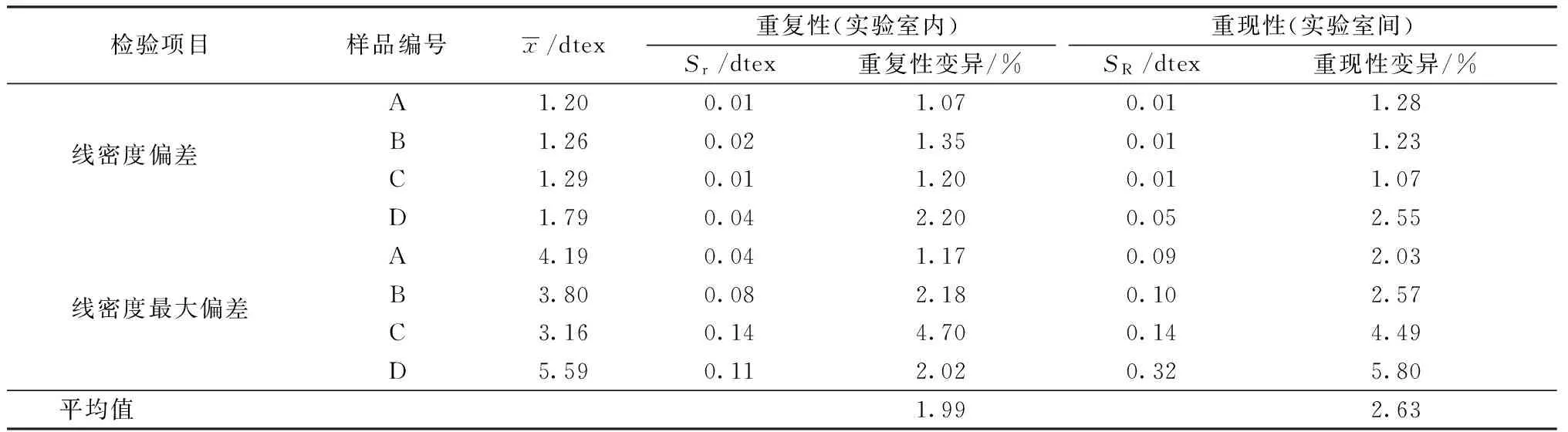
檢驗項目樣品編號x/dtex重復性(實驗室內)重現性(實驗室間)Sr/dtex重復性變異/%SR/dtex重現性變異/%A1.200.011.070.011.28線密度偏差 B1.260.021.350.011.23C1.290.011.200.011.07D1.790.042.200.052.55A4.190.041.170.092.03線密度最大偏差B3.800.082.180.102.57C3.160.144.700.144.49D5.590.112.020.325.80平均值 1.992.63

表2示出抽樣方法方案的檢測結果。試驗設計中考慮了所檢測物料的非均質性。表中實驗室間變異明顯高于實驗室內變異，同時也明顯高于表1中的檢測結果。這說明各實驗室所檢測的樣本雖來自同一批絲，采用同一種抽樣方法與樣本容量，但是同一批絲各樣本存在較大差異，更進一步說明了物料的非均質性是精密度試驗產生變異的主要原因。而精密度試驗主要目的即是要發現變異，因此，在線密度檢測方法的實際使用中應將物料的非均質性所產生的變異包含在測量方法精密度中。此外，表2中的精密度數據雖然較表1偏大，重復性變異平均在10%左右，但是仍能表明其重復性與重現性水平較高。

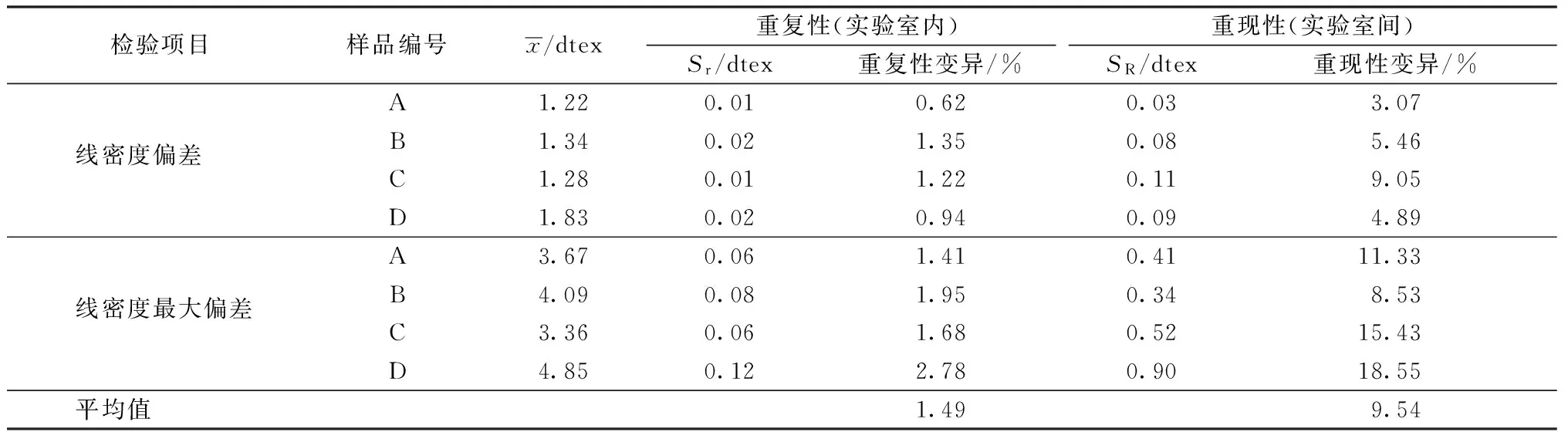
表2 抽樣方法試驗方案中生絲線密度檢驗的試驗精密度

4 結 論

本文對不同規格生絲線密度檢驗方法進行了實驗室比對試驗，設計了2種試驗方案，即循環比對試驗方案和抽樣方法試驗方案。前者是對同一批絲抽取同一樣本交由各實驗室循環測量；而后者則是對同一批絲按同一抽樣方法、樣本容量規定抽取5個不同的樣本分別交由5個不同的實驗室進行檢測。通過對檢測結果分別計算試驗精密度，即重復性與重現性標準差和變異，并進行分析，可以得出以下結論：1)在進行線密度檢驗方法的精密度計算時需考慮生絲樣本非勻質性所產生的變異；2)在考慮生絲樣本非勻質性時所進行的精密度試驗結果表明，該試驗方法的重復性與重現性較高，檢驗方法與樣本容量合理。

FZXB

[1] 白倫. 關于生絲檢驗分級標準及其研究的歷史考察[J]. 絲綢史研究, 1984, 3(3): 1-7. BAI Lun. Historical investigation on the classification standard of the raw silk test and its research[J]. Silk History Research, 1984, 3(3): 1-7.

[2] The Raw Silk Classification Committee of America. Standard Tests for Raw Silk[M]. New York: The Saratogian Printing Service, 1922:24,27.

[3] 徐明荃. 自動繅絲絡交張力的降低及其對生絲的影響[D]. 蘇州：蘇州大學，2013: 7-8. XU Mingquan. Tension reduction in automatic silk reeling process and its effect on the raw silk[D]. Suzhou: Soochow University, 2013: 7-8.

[4] 白倫，謝佳，李林甫.關于縮短生絲纖度偏差檢驗絲長問題的研究[J]. 絲綢, 2000 (1): 7-13. BAI Lun, XIE Jia, LI Linfu. Research on shortening the test length in the raw silk size test[J]. Journal of Silk, 2000 (1): 7-13.

[5] 牛建濤, 許建梅.生絲電子檢驗中線密度變異系數的分布[J]. 紡織學報, 2013, 34(1): 21-25. NIU Jiantao, XU Jianmei. Distribution of coefficient of linear density variation of raw silk in electronic testing[J]. Journal of Textile Research, 2013, 34(1): 21-25.

[6] 劉欣，陳慶官. 基于NI-cRIO的生絲實時電子檢測系統的開發[J]. 紡織學報，2010，31(12):112-115. LIU Xin, CHEN Qingguan. Development of reel-time electronic detection system for raw silk based on NI-cRIO [J]. Journal of Textile Research, 2010, 31(12):112-115.

[7] XU Jianmei, BAI Lun, WU Dongping, et al. Grading standards of the coefficient of variation in the electronic raw silk size testing[J]. Journal of Donghua University, 2007, 24(2): 235-239.

[8] 陳慶官, 戴新蘭, 夏永林. 印度、韓國、巴西生絲檢驗標準與ISA標準[J]. 四川絲綢, 2005 (1): 44-48. CHEN Qingguan, DAI Xinlan, XIA Yonglin. Raw silk test standard of India, Korea, Brazil and ISA[J]. Journal of Sichun Silk, 2005 (1): 44-48.

[9] 周穎. 國生絲新標準與國外生絲標準對比[J]. 絲綢, 2009 (11): 35-41. ZHOU Ying. Comparison and analysis between Chinese standard and foreign standard of raw silk[J]. Journal of Silk, 2009(11): 35-41.

[10] 胡祚忠, 葉晶晶, 吳建梅,等.生絲國際標準的研究制定[J]. 絲綢, 2014, 51(7): 26-31. HU Zuozhong, YE Jingjing, WU Jianmei, et al. Research and formulation of international standard for raw silk [J]. Journal of Silk, 2014,51(7): 26-31.

[11] 蔣小葵. 熟練運用生絲標準破解印度反傾銷[J].絲綢, 2009 (7): 6-12. JIANG Xiaokui. Handling the Indian anti-dumping by sophisticatedly using raw silk standard[J]. Journal of Silk, 2009(7): 6-12.

Evaluation and measurement of precision for raw silk linear density test

XU Jianmei1，2， ZHOU Ying3， LI Chun4， WU Dongping3， BAI Lun1

(1.CollegeofTextileandClothingEngineering,SoochowUniversity,Suzhou,Jiangsu215021,China; 2.NationalEngineeringLaboratoryforModernSilk,Suzhou,Jiangsu215123,China; 3.ZhejiangSilkTechnologyCo.,Ltd.,Hangzhou,Zhejiang310011,China; 4.GuangdongEntry-ExitInspectionandQuarantineBureau,Guangzhou,Guangdong510623,China)

To evaluate the precision (repeatability and reproducibility errors) of raw silk linear density test using raw silk linear density tester, and find the affecting extent of heterogeneous material on test precision, the precision data of linear density test for different specifications of raw silk was obtained when the sample size is 200 skeins with each skein having a length of 100 revolutions (112.5 m). Two different test schemes were designed for this study. The first scheme is to carry out cycling comparison trial among five laboratories on the same samples, and the other is to test five different samples from the same lot of raw silk by five laboratories, respectively. The test data show that the precision level is very high when using the same samples and the average coefficients of repeatability variation and reproducibility errors are less than 3%, while the average coefficients are above 10% when using different samples. Therefore, it can be concluded that the heterogeneity of material has great effect on the precision of raw silk linear density test, and the heterogeneity of material should be considered in evaluating and measuring the precision of raw silk linear density test in order to obtain the accurate precision level of the actual test.

raw silk; linear density test； accuracy； heterogeneity； sample size

10.13475/j.fzxb.20150805005

2015-08-31

2016-06-10

國家自然科學青年基金項目(51303117)；質檢公益性行業科研專項項目(201310215)

許建梅(1976—)，女，副教授，博士。主要研究方向為生絲檢驗與抽樣分級理論及人工神經導管的三維構建與評價。E-mail：xujianmei@suda.edu.cn。

TS 147

A