組織工藝參數對經編送經量的影響

張吉生， 蔣高明

(江南大學 教育部針織技術工程研究中心， 江蘇 無錫 214122)

組織工藝參數對經編送經量的影響

張吉生， 蔣高明

(江南大學 教育部針織技術工程研究中心， 江蘇 無錫 214122)

為提高經編送經量的預測精度，測試了5種不同組織工藝參數下38種試樣的送經量，并采用IBM SPSS19進行單因素分析和多元線性回歸分析，得出各組織工藝參數因素與送經量間的關系；建立送經量多元線性回歸預測模型。研究結果表明：針背橫移、針前橫移與送經量成正相關且影響程度大，牽拉密度、機號與送經量成負相關且影響程度較小，總穿經率對送經量的影響程度很小；組織工藝參數對送經量影響程度由大到小排序依次為針背橫移、針前橫移、牽拉密度、機號和總穿經率；得出的多元線性預測模型具有較好預測精度，可為送經量的預測提供一定的參考。

送經量； 經編； 組織工藝參數； 線性回歸

送經量為編織480橫列各梳櫛所耗紗線的長度(單位為mm/臘克)，是經編織物生產中的重要工藝參數[1]。此前送經量的預測研究主要集中在以模擬線圈幾何模型進行估算方面[1-3]，但由于經編織物的復雜性，送經量影響因素較多，單一的幾何模型仍難以精確預測送經量。目前，經編織物在設計方面已實現CAD數值化設計；在生產方面實現了橫移機構與送經機構的自動化[4]。但由于缺少準確預測送經量的方法，經編織物的設計與生產調試仍需依靠技師反復上機調試，耗費較多時間、人力及原料[5-6]。為研究織物組織工藝參數對送經量的影響，并為經編送經量的預測提供一定的參考，本文通過測試針前橫移、針背橫移、牽拉密度、總穿經率和機號等5種組織工藝參數在不同取值下的送經量值，并將結果進行單因素和多因素分析，得出各組織工藝參數與經編送經量間的關系及送經量的多元線性預測模型。

1 試驗部分

1.1 影響因子選取

織物組織工藝參數是影響送經量的主要因素，其主要包括：針前橫移、針背橫移、牽拉密度、機號、總穿經率。針前橫移與針背橫移由經編組織墊紗數碼所決定，其中針前橫移針數決定該梳櫛是否形成線圈結構；針背橫移則影響延展線跨越的針數從而影響送經量的大小。牽拉密度即織物的機上縱密影響線圈長度；機號決定相鄰織針間距，為梳櫛移動單針的距離的主要因素，從而影響延展的長度；總穿經率即各把梳櫛穿經率之和，可能影響線圈圈弧的大小，因此，本文選取上述5種影響送經量的織物組織工藝參數作為單針床經編送經量的主要影響因子；各織物組織參數及其常規最大值和最小值如表1所示。

表1 影響因子及其常規取值范圍

1.2 試驗儀器與原料

送經量測定采用德國卡爾邁耶公司生產的3臺機號分別為E24、E28和E32的HKS4_EL單針床特里科型高速經編機。該機型具有電子橫移系統更改組織參數方便且具備可精確測量送經量的EBC積極送經系統，送經量測量誤差為±0.1%。采用德國施密特ZF-02型紗線張力測量儀測量試織過程中的經紗張力[7-8]。選用福建錦江科技有限公司生產的線密度適中的6.67 tex/24 f滌綸FDY為測量送經量所用原料；送經量測試在室溫為(25±2)℃、相對濕度為(65±4)%的環境下進行。

1.3 試驗方法

本文結合單因素試驗與正交試驗，選取38個具有不同組織工藝參數的經編織物為測試樣本，試樣的工藝參數如表2所示。

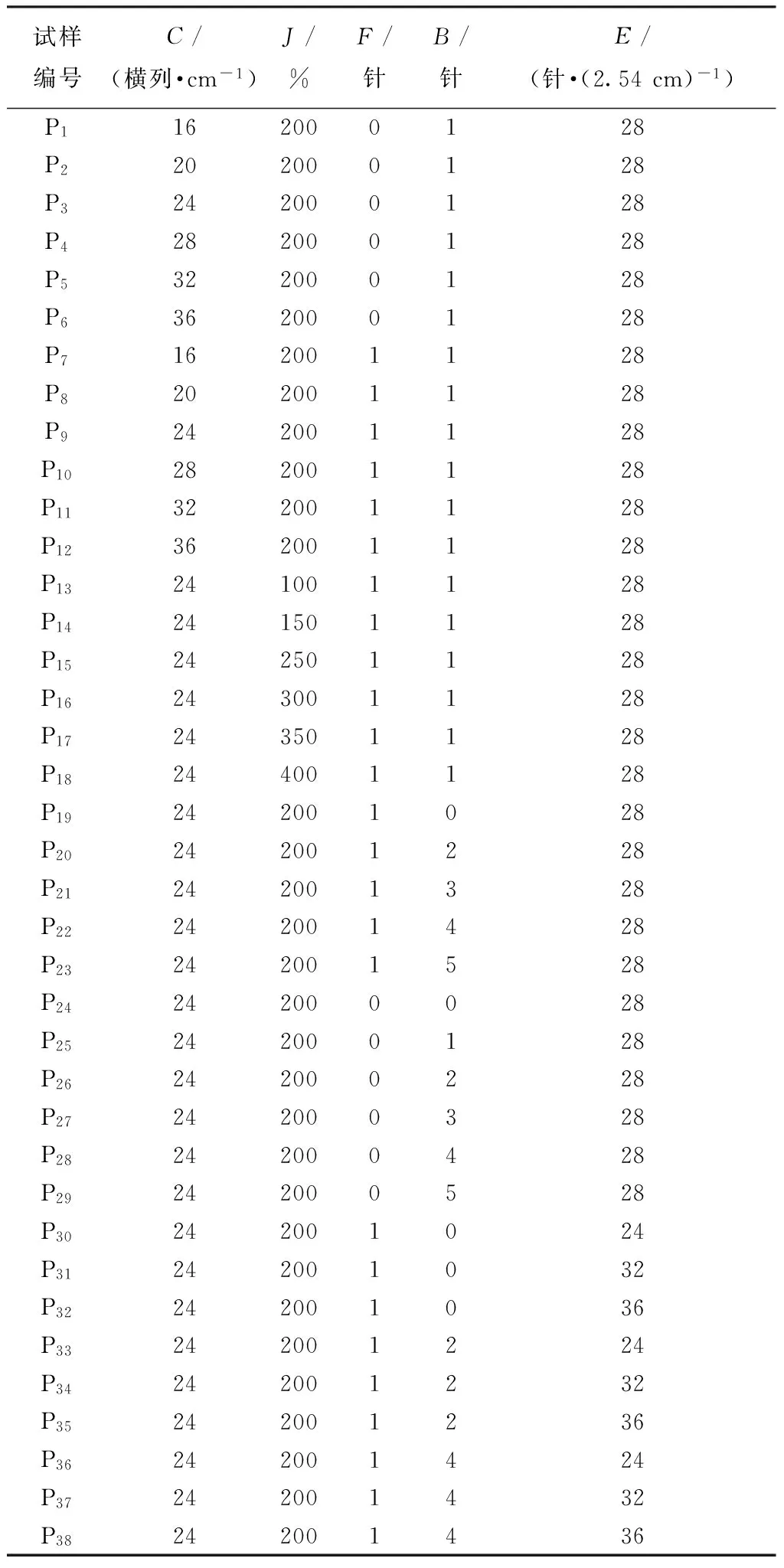
表2 試樣工藝參數

所需送經量值的測定。試織過程中調整送經量，并測量織造過程中的經紗張力。被測樣本送經量調試完成的評定依據為：以單根經紗平均張力為(3±0.5)cN且試樣可于800 r/min的機速下穩定織造5 min無斷紗。每個試樣測試3次取平均值。運用IBM SPSS19[10]對單因素試驗測試結果進行單元線性回歸，分析在其余組織工藝參數不變的情況下，各因子對送經量的影響；以極差值法對正交試驗測試結果進行無量綱化處理，并使用IBM SPSS19對標準化數據進行多元線性回歸，分析各組織工藝參數對送經量的影響權重并推導經編送經量多元線性預測模型。

2 結果與討論

2.1 單因素分析結果

2.1.1 牽拉密度對送經量的影響

F=1針表明該梳櫛形成線圈；F=0則表示組織不成圈，僅形成延展線。圖1示出牽拉密度與送經量間關系的線性擬合曲線，其中B=1針、J=200%、E=28針/2.54 cm。

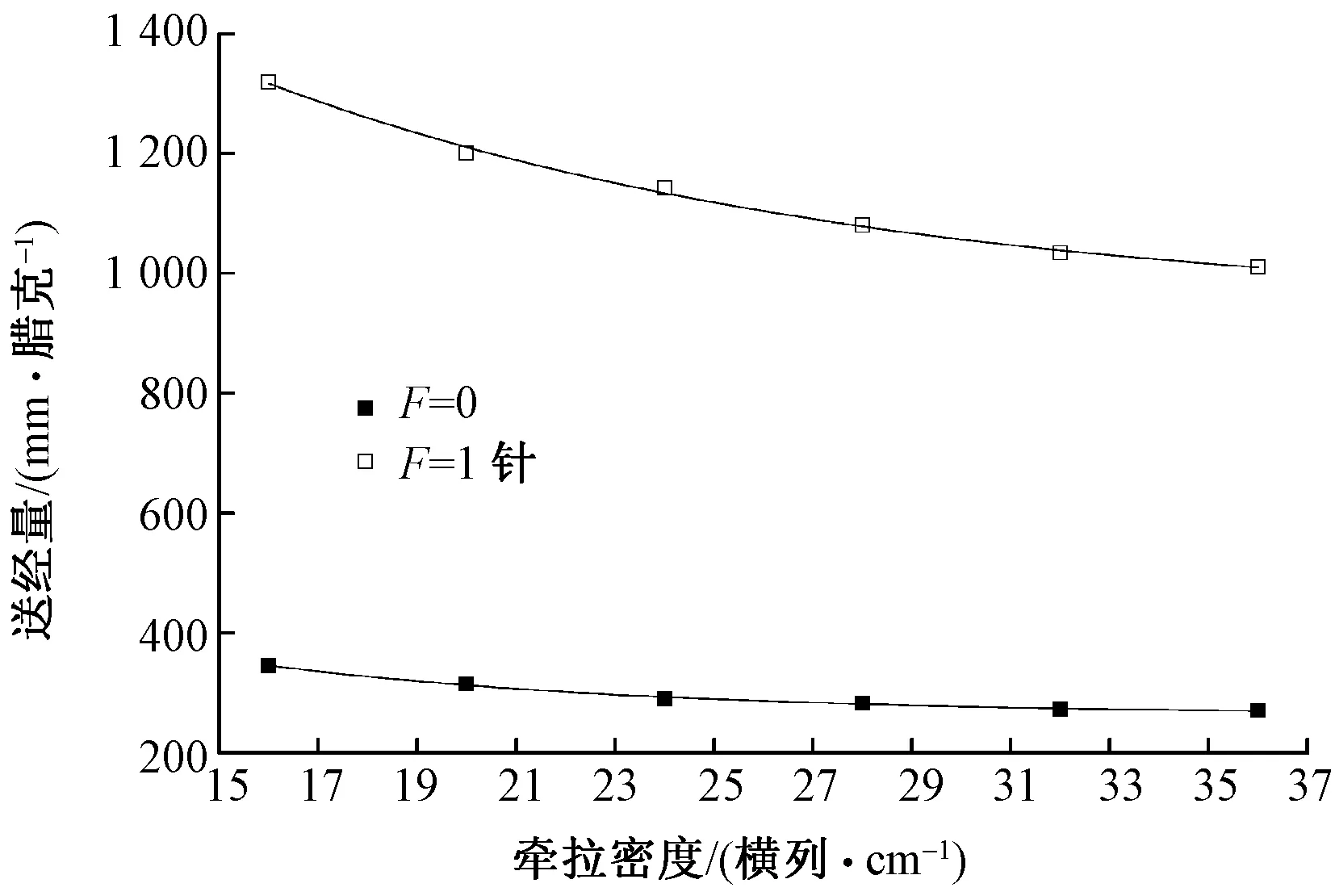
圖1 牽拉密度與送經量間的關系

如圖1所示，在成圈或不成圈的2種情況下，隨著牽引密度C增大，送經量均逐漸減小；當F=0時，牽拉密度與送經量的回歸方程見式(1)；當F=1針時，牽拉密度與送經量的回歸方程見式(2)。

y=-398.3lnC+2 423.8，R2=0.98

(1)

式中y表示送經量，mm/臘克。

y=-93.2lnC+595.9，R2=0.95

(2)

由此表明在其余工藝參數相同的條件下，送經量與牽拉密度呈現負相關；隨牽拉密度的增大，送經量呈對數型減小，且減小速度逐漸趨緩。

2.1.2 針背橫移對送經量的影響

圖2為針背橫移對送經量影響的線性擬合圖，其中C=24橫列/cm、J=200%、E=28針/2.54 cm。

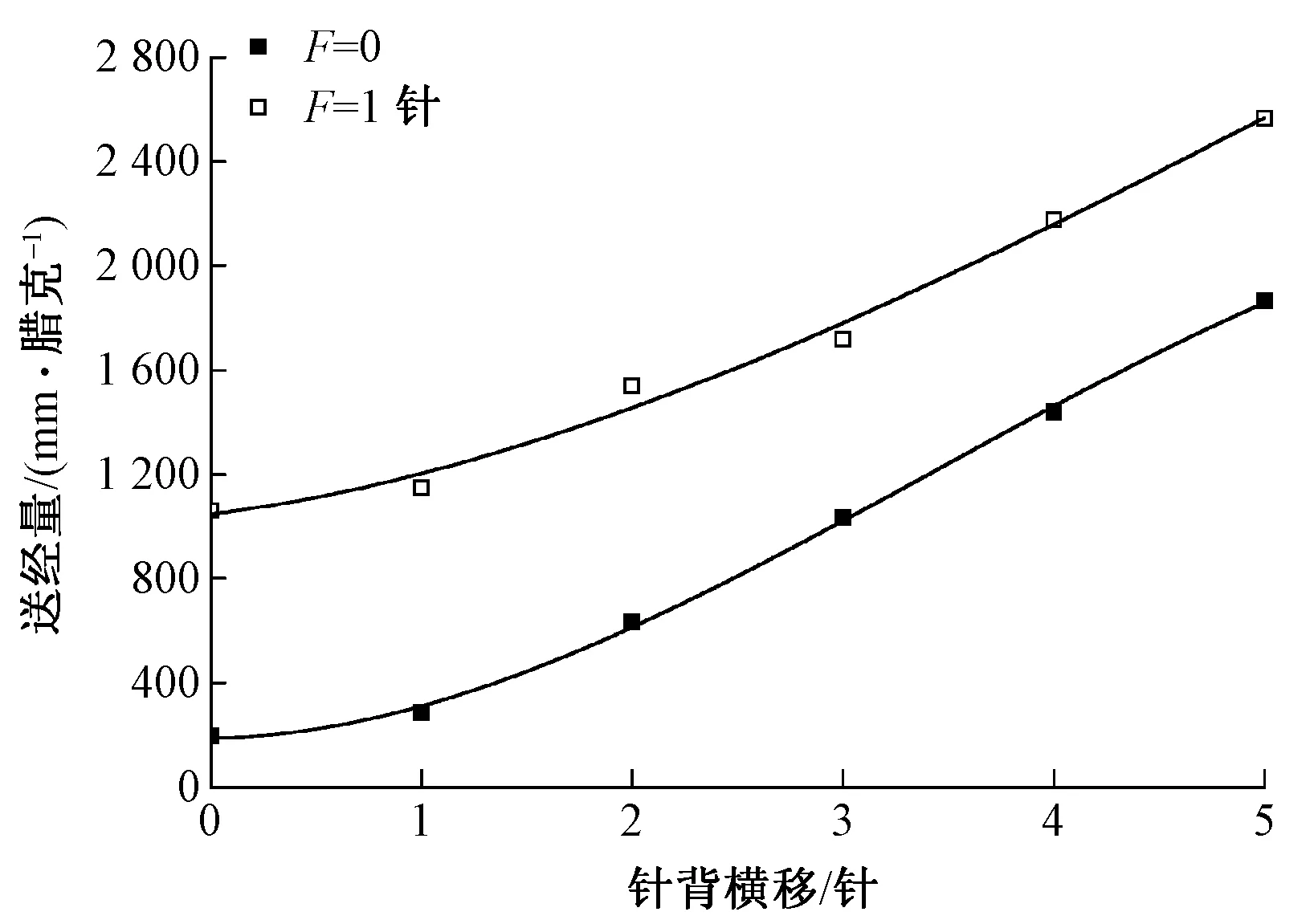
圖2 針背橫移與送經量間的關系

如圖2所示，在成圈與不成圈2種狀態下，隨著針背橫移B由0增大至5針時，送經量均呈增大趨勢。當F=1針時，針背橫移與送經量間關系的回歸方程如式(3)所示；當F=0時，針背橫移與送經量間關系的回歸方程如式(4)所示。當針背橫移由0增大到1針時，送經量增加較緩慢；當針背橫移由1針增大到2針時，送經量增大速度相比由0增大到1針時顯著提高；當針背橫移由2針增大至5針時送經量趨于線性增加。由此表明，在其余工藝參數不變的條件下，針背橫移針數與送經量間成二次項型正相關。

y=31.6B2+150.7B+1 036.3，R2=0.99

(3)

y=34.2B2+178B+149，R2=0.98

(4)

2.1.3 針前橫移對送經量的影響

如圖1、2所示，F為1針時的送經量值與F為0時的值相比均有明顯增長，其最小增長幅度為37%，最大增長幅度為443%，平均增長幅度為229%。由此可見，針前橫移與送經量呈顯著正相關，針前橫移對送經量影響程度高。當B=1針、J=200%、E=28針/2.54 cm時，如圖1所示，隨著牽拉密度的增大，F為1針與F為0這2種情況下的送經量差值逐漸減小，說明牽拉密度越小，針前橫移對送經量的影響越顯著；如圖2所示，隨針背橫移的增大，F為1針所需的送經量與F為0所需送經量的差值逐漸緩慢減小，說明隨針背橫移的增大，針前橫移對送經量影響的顯著性略有下降。

2.1.4 機號對送經量的影響

圖3示出機號與送經量間的線性關系，其中F=0、C=24橫列/cm、J=200%。

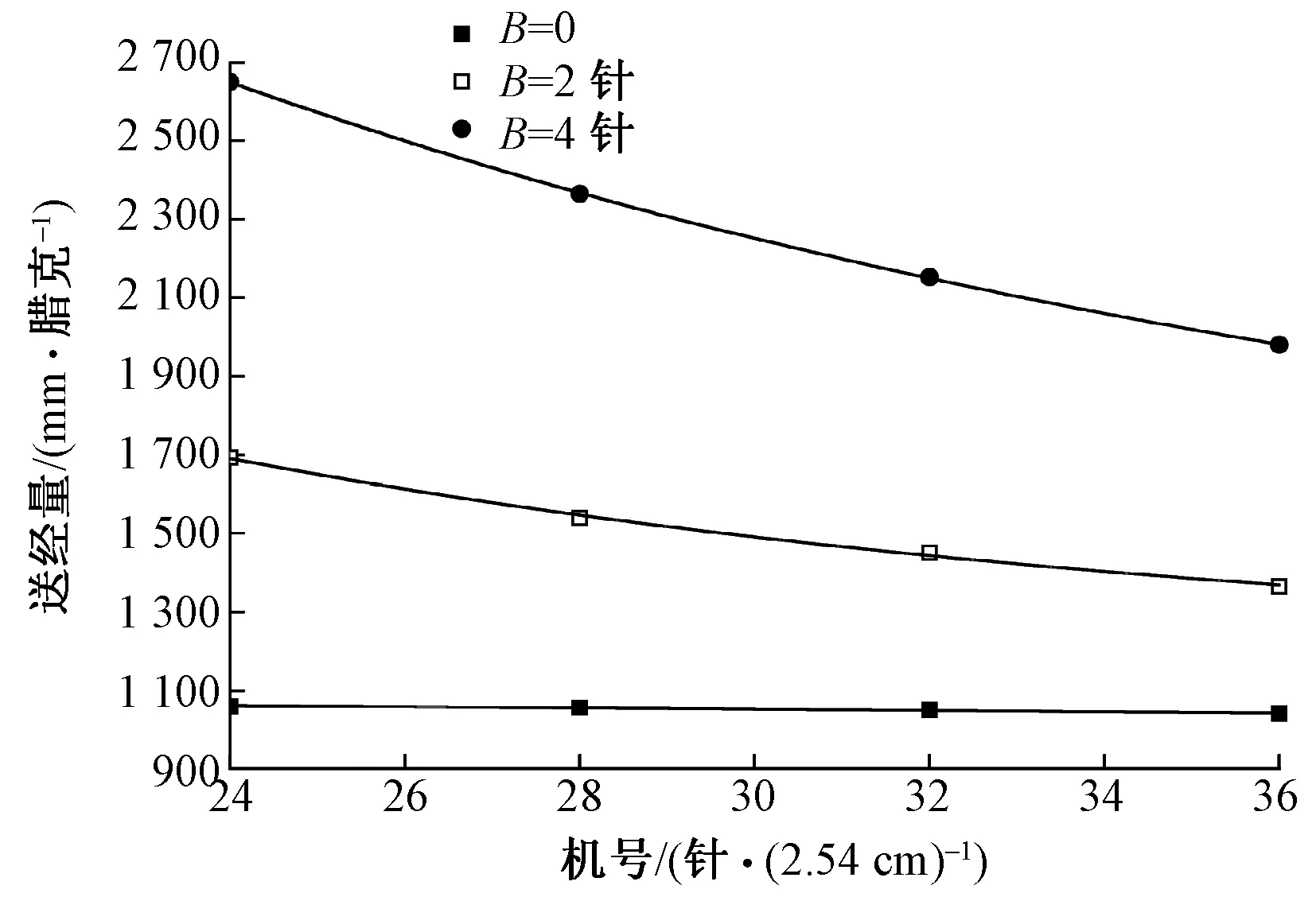
圖3 機號與送經量間的關系

如圖3所示，隨機號E的增大，送經量逐漸減小且減小的速度逐漸放緩。由于因子E主要影響針背橫移單針的距離，因此當針背橫移B針數越大時，隨機號的增大，送經量的減小速度越快。當B=0時，機號與送經量間關系的回歸方程如式(5)所示；當B=2針時，機號與送經量間關系的回歸方程如式(6)所示；當B=4針時，機號與送經量間關系的回歸方程如式(7)所示。由此表明，在其余工藝參數不變的前提下，機號與送經量成指數型負相關；由于系數為-0.001，易知-0.001E變化幅度很小，因此表明當B=0針時，機號對送經量的影響很小，可忽略；比較式(5)、(6)、(7)中系數，易知0.024>0.018>0.001且4 711>2 555>1 099，可見隨B的增大，機號對送經量的影響越來越明顯。

y=1 099e-0.001E，R2=0.96

(5)

y=2 555e-0.018E，R2=0.98

(6)

y=4 711e-0.024E，R2=0.99

(7)

2.1.5 總穿經率對送經量的影響

圖4示出總穿經率與送經量間的關系，其中F=0、B=1針、C=24橫列/cm、E=28針/2.54 cm。

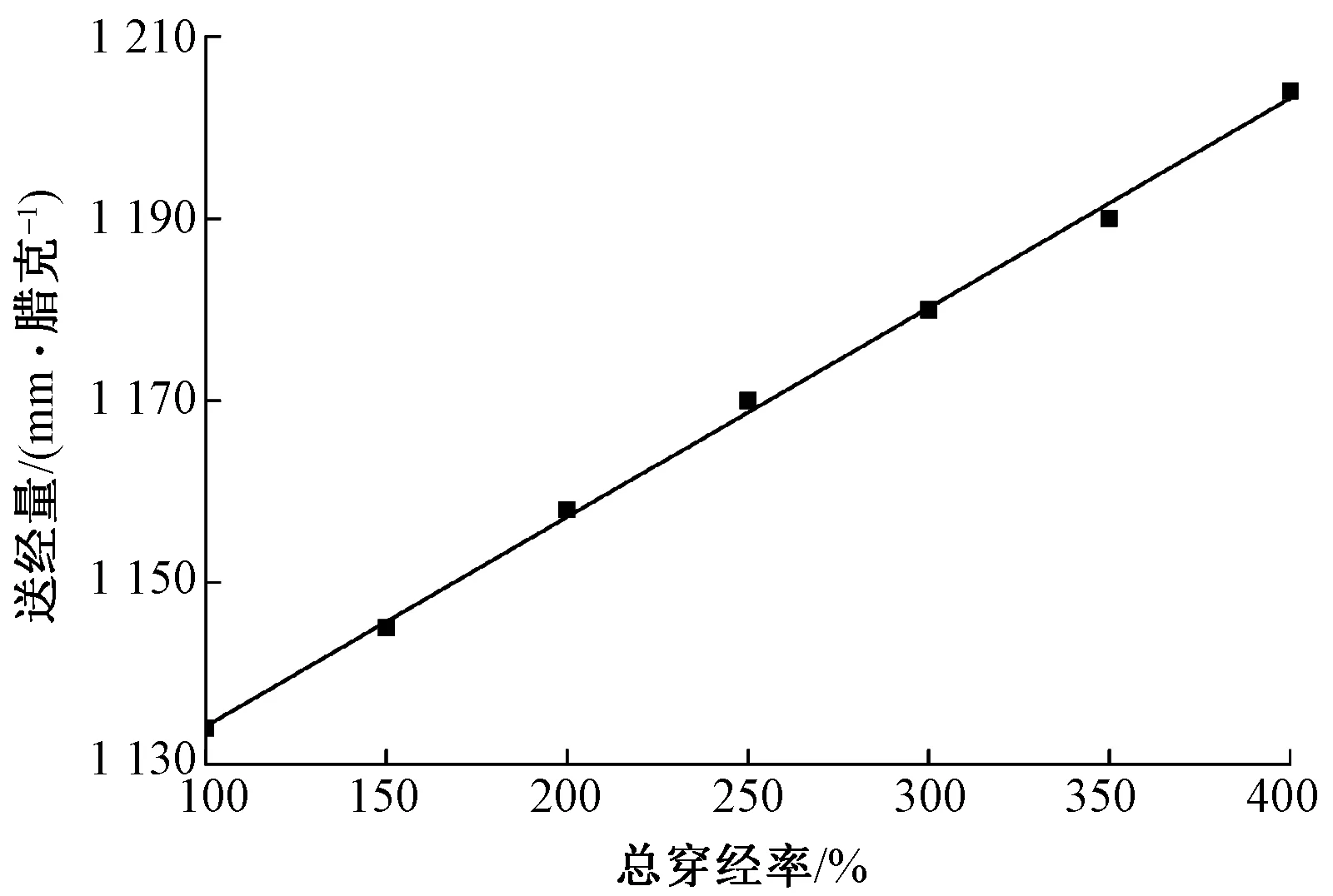
圖4 總穿經率與送經量間的關系

如圖4所示，當總穿經率J由100%增大至400%時，送經量逐漸增大，且增大的速度基本保持一致。總穿經率與送經量間關系的回歸方程如式(8)所示；當總穿經率由100%增大3倍至400%時，送經量僅增大6.17%，增長幅度較小。由此可見，當其余組織工藝參數不變時，總穿經率與送經量間成線性正相關，并且其對送經量的影響程度很小。

y=0.23J+1 111.2，R2=0.99

(8)

2.2 多元回歸分析結果

2.2.1 各因子對送經量影響的顯著性分析

對各因子分別進行單元線性回歸分析，各回歸方程的相關系數R2均大于0.90，表明各自變量與送經量間具有較為顯著的線性關系，可使用多元線性回歸的方法分析各因子的影響權重。首先采用極差法，如式(9)所示，對變量進行標準化處理以消除量綱，自變量的極大和極小值如表1所示；然后運用SPSS19以進入法進行多元線性預回歸分析，回歸系數R2為0.96，說明各因子與送經量間存在較顯著的線性關系，回歸模型具有較高可靠性。

(9)

式中，J′、C′、F′、B′、E′、y′分別表示與J、C、F、B、E、y無量綱化后的標準值。

各因素與送經量間顯著性如表3所示。其中因子J的Sig.值大于0.05且統計量t值為0.139，表明J與送經量間關聯顯著性低，在各因子中對送經量影響程度最小；其余因子的Sig.值均小于0.05且統計量t值均大于1，說明除J外的其余因子對送經量影響較為顯著。由于F與B的非標準系數大于0，表明F、B與送經量呈正相關；C與E的非標準系數小于0，可得C、E與送經量呈負相關；由于各因子回歸系數絕對值由大到小排序為1.135>0.654>|-0.382|>|-0.214|且統計量t絕對值排序順序相同，因此組織工藝參數對送經量影響程度由大到小排序依次為：針背橫移、針前橫移、牽拉密度、機號和總穿經率。針背橫移和針前橫移對單針床經編送經量的影響程度高；牽拉密度與機號的影響程度相對較小；總穿經率對送經量影響程度很小。

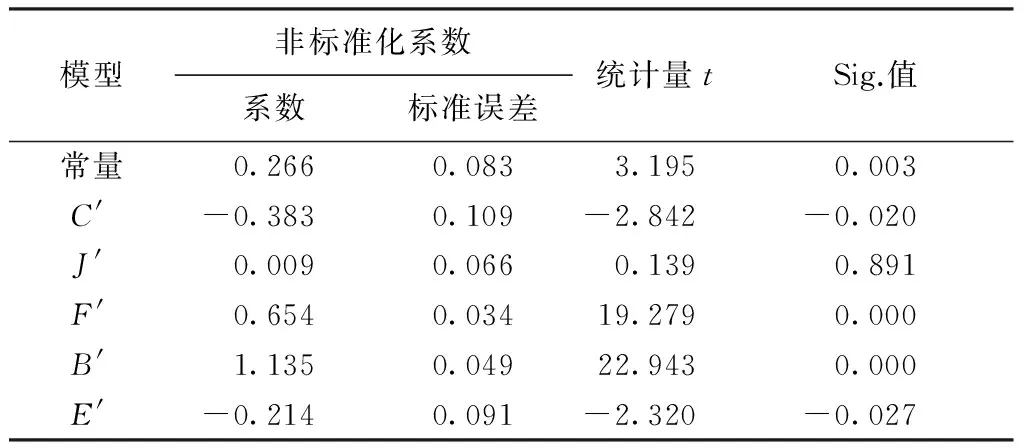
表3 多元回歸系數及因子顯著性

2.2.2 送經量多元回歸預測模型

2.2.2.1 預測模型的建立 由于因子J的Sig.值過大，不具有統計學意義，因此將因子J從多元線性預測模型中剔除；由表3可知標準化的送經量回歸預測方程如式(10)所示。將式(9)代入式(10)中，可得基于織物組織工藝參數的經編送經量多元線性回歸模型，如式(11)所示；回歸系數R2為0.96，說明該多元線性預測模型可解釋絕大數的測試樣本，具有較高的擬合度，因此可為經編送經量的預測提供一定參考。

y′=0.266-0.383C′+0.654F′+

1.135B′-0.214E′

(10)

y=855.3-20.3C+866.6F+

334.2B-14.9E

(11)

2.2.2.2 模型檢驗 通過將織物的實測送經量與預測送經量值進行比較，可對多元線性回歸模型的送經量預測精度進行檢驗。在單針床經編織物中隨機選取3個檢驗樣本。將樣本織物組織工藝參數代入預測模型，如式(11)，易得檢驗樣本的送經量模型預測值。

表4示出檢驗樣本織物的工藝參數及樣本的實測送經量與模型預測值的比較結果。由表可知， 6把梳櫛的送經量預測值的誤差均在±15.8%的范圍內，且預測平均預測誤差為8.53%。由此表明：該送經量多元線性回歸預測模型具有較高的預測精度，且可較好地描述組織工藝參數對單針床經編送經量的影響。

表4 實測送經量與模型預測值的對比

注：GB表示由機前向機后的梳櫛序號；穿經方式均為滿穿。

3 結 論

1)單因素分析表明，在其余工藝參數相同的條件下，牽拉密度與送經量呈現負相關，隨牽拉密度的增大送經量呈對數型減小，且減小速度逐漸趨緩。針背橫移與送經量成二次項型正相關；針背橫移大于1針后，送經量增大速度加快。針前橫移與送經量成顯著正相關，針前橫移對送經量影響的顯著性隨針背橫移的增大略有下降。機號與送經量呈指數型負相關；隨針背橫移的增大，機號對送經量的影響越來越明顯。總穿經率與送經量間呈線性正相關且對送經量的影響程度較小。

2)多因素影響分析表明工藝組織參數對送經量影響程度由大到小排序依次為：針背橫移、針前橫移、牽拉密度、機號和總穿經率；在組織工藝參數中，針背橫移與針前橫移是送經量的主要影響因素；牽拉密度與機號是次要影響因素；總穿經率對送經量的影響很小，可忽略。由多元線性回歸得到基于織物組織工藝參數的單針床經編送經量預測模型，可為經編送經量的預測提供理論參考。

FZXB

[1] 董智佳, 蔣高明. 經編提花無縫服裝的成型結構與設計[J]. 紡織學報, 2012, 33(1): 102-106. DONG Zhijia, JIANG Gaoming. Shaping structure and design method of warp knitted jacquard seamless garment [J]. Journal of Textile Research，2012，33(1): 102-106.

[2] 蔣高明. 經編針織物生產技術[M]. 北京：中國紡織出版社, 2010:581-583. JIANG Gaoming. Production Technology of Warp-knitted Fabric[M]. Beijing: China Textile & Apparel Press, 2010:581-583.

[3] DABIRYAN H, JEDDI A. Analysis of warp-knitted fabric structure part[J]. Journal of the Textile Institute, 2012，102(12): 1352-1360.

[4] 冒海文, 繆旭紅,陳晴,等. 滌綸長絲仿棉經編運動面料的生產工藝[J]. 紡織學報, 2015, 36(8): 89-93. MAO Haiwen, MIAO Xuhong, CHEN Qing, et al. Production process of polyester filament warp-knitted sportswear fabric with high simulated cotton appearance[J]. Journal of Textile Research, 2015, 36(8): 89-93.

[5] 李欣欣, 蔣高明, 張愛軍, 等. 經編提花間隔織物的計算機輔助設計[J].紡織學報, 2015, 36(2): 105-110. LI Xinxin, JIANG Gaoming, ZHANG Aijun, et al. Computer-aided design of warp-knitted jacquard spacer fabrics [J]. Journal of Textile Research, 2015, 36(2): 105-110.

[6] 張吉生, 吳志明. 經編無縫女束身上衣成形方法研究[J]. 紡織學報, 2012, 33(12): 107-111. ZHANG Jisheng, WU Zhiming. Research on the forming method of warp knitting seamless tunic blouse[J]. Journal of Textile Research, 2012, 33 (12): 107-111.

[7] HALLOS R S, SUN F. The analysis and comparison of three prediction methods for run-in in raschel warp-knitting[J]. Journal of the Textile Institute, 1997, 88(3): 282-304.

[8] MA Pibo, JIANG Gaoming, CHEN Qing, et al. Experimental investigation on the compression behaviors of epoxy with carbon nanotube under high strain rates[J]. Composites Part B, 2015, 69(1): 526-533.

[9] MA Pibo, GAO Zhe. A review on the impact tension behaviors of textile structure composites[J]. Journal of Industrial Textiles, 2013, 44(4): 572-604.

[10] 楊小平. 統計方法與SPSS應用教程[M]. 北京：清華大學出版社, 2008: 4-23. YANG Xiaoping. Statistical Methods and Applied Tutorial of SPSS[M]. Beijing: Tsinghua University Press, 2008: 4-23.

Influence of weave parameters on warp-knitted run-in values

ZHANG Jisheng, JIANG Gaoming

(EngineeringResearchCenterforKnittingTechnology,MinistryofEducation,JiangnanUniversity,Wuxi,Jiangsu214122,China)

To improve prediction accuracy of warp knitting run-in values, run-in values of 38 samples with 5 different weave parameters were measured. Then, experimental results were analyzed by IBM SPSS19 to research the relationship between run-in values and fabric weave parameters. Moreover, a multiple linear regression model for forecasting run-in values were suggested. It is indicated by the result that both of overlap shogging and underlap shogging have significant positive correlation with the run-in values. Both of take-up density and machine gauge have negative correlation with run-in values. The run-in values are slightly positively affected by total rate of threading. The impact significance of the 5 factors from big to small is in the order of underlap shogging, overlap shogging, take-up density, machine gauge and total rate of threading. Furthermore, a multiple linear regression model was obtained to provide reference for predicting run-in values.

run-in value； warp knitting； weave parameter； linear regression

10.13475/j.fzxb.20151002206

2015-10-10

2016-04-22

中央高校基本科研業務費專項資金資助項目(JUSRP51404A)；江蘇省自然科學基金資助項目(BK20151129)；江蘇省產學研聯合創新資金-前瞻性聯合研究項目(BY2015019-20)

張吉生(1988—)，男，博士生。主要研究方向為經編送經量的預測。蔣高明，通信作者，E-mail: jgm@jiangnan.edu.cn。

TS 106.56

A