“冰桶挑戰(zhàn)”誘導的社交網絡演化分析

楊　凱,劉曉露,林堅洪,成　曦,郭　強,劉建國

(上海理工大學復雜系統科學研究中心，上海 200093)

?

“冰桶挑戰(zhàn)”誘導的社交網絡演化分析

楊凱,劉曉露,林堅洪,成曦,郭強,劉建國

(上海理工大學復雜系統科學研究中心，上海 200093)

摘要:考慮社交網絡初始階段的演化過程對于定量認識和理解人際關系的形成與演化的重要意義，搜集“冰桶挑戰(zhàn)”事件國內從事件發(fā)起到第6天的數據。以挑戰(zhàn)者為節(jié)點，點名關系為邊構造社交網絡。通過分析該網絡的統計指標，發(fā)現網絡密度一直減小；網絡效率先減小，后又緩慢增加；連通子圖的數量先迅速增加，最高增加了初始值的5倍，后又減小；網絡效率與子圖數量呈負相關關系。考慮到該網絡構建的特殊性，與其他社交網絡的演化做了對比分析。

關鍵詞：社交網絡；網絡演化；拓撲結構；冰桶挑戰(zhàn)

0引言

社會網絡是描述社會關系的工具之一[1]。社交網絡誕生初期的發(fā)展和演化對于理解人際關系的演化至關重要。2001年秋，哥倫比亞大學社會系的Watts等[2]建立了一個小世界項目的網站，開始在世界范圍內進行一個檢驗六度分離假說是否正確的網上在線實驗，該實驗的目的是為了驗證幾十億人口的整個世界是否有小世界現象。在一年多的時間里，總共有13個國家的18名目標對象和166個國家和地區(qū)的6萬多名志愿者參與實驗，最后有384個志愿者的電子郵件抵達了目的地。每封郵件平均轉發(fā)5到7次即可到達目標對象。在Web2.0應用模式下[3]，網絡人際關系可通過新的方式重新構建。社交網絡服務(social networking services，SNS)和微博(如新浪微博、Twitter)是最新出現的兩種Web2.0應用模式，都屬于在線社交網絡[4]。針對社交網絡的演化[5]，很多學者基于理論模型做了分析，復雜網絡中兩個較早且比較著名的模型是小世界模型[6-7]和無標度模型[8]。張立等[9]在虛擬的社區(qū)網絡上做了演化分析，并研究其拓撲結構。發(fā)現虛擬社區(qū)網絡在演化過程中,節(jié)點的加入、邊的加入、網絡中度分布、節(jié)點的度與其加入網絡時間的關系、平均度隨時間的變化等方面與傳統的無標度網絡有所不符。熊熙等[10]考慮社交網絡的聚類及連接隨機性提出了一種混合演化模型。數值仿真表明該網絡模型與實際社交網絡數據的統計結果基本吻合。Ravi Kumar等[11]實證分析了大型在線社會網絡結構的演化，并提出了一種能識別組元結構的網絡增長模型，但他們僅僅截取了網絡中間的部分數據，并沒有從網絡誕生時開始分析。信息及輿論在社交網絡上的傳播過程[12]也可以看作是一個網絡演化的過程，當信息傳播到一個用戶時，那么該用戶加入了這個信息網絡。當前對于社會網絡演化的研究無論從模型還是實證角度都是基于全網絡的演化，并非局部關系的演化。

本文搜集了國內“冰桶挑戰(zhàn)”事件從發(fā)起到發(fā)展到第6天的數據，以天為單位將數據劃分，構造了不同時間上的網絡。按照該活動的規(guī)則，該社交網絡具有其特殊性——選擇自己的親密好友所構建的網絡，可認為網絡中邊的關系為強關系。該網絡相當于一般社交網絡的一個“骨架”，是非常重要的結構。本文首先給出了該網絡每天的演化過程，分析了該網絡的密度、聚類系數及網絡效率等結構特性，發(fā)現網絡密度從開始的0.120 9逐漸下降，與Yahoo!360網絡的密度演化有明顯區(qū)別。聚類系數從初始值零增加到0.016 7后又緩慢減小，而整體聚類系數相對較小；網絡效率先減小，從0.214 3降到最小值0.039 9，后又緩慢增加。聚類系數與網絡效率這兩個方面與Facebook網絡上的演化也有異同，本文分析了其中的原因，而對比分析可以體現出本文網絡的特殊性。最后，分析了網絡的最大連通子圖，連通子圖的數量先迅速增加最高增加了初始值的5倍，后又減小。發(fā)現連通子圖的數量與網絡效率成負相關關系。本文的研究可以為構建相應的理論模型提供一定依據。

1數據描述與網絡構建

1.1數據描述

“冰桶挑戰(zhàn)”全稱為“ALS冰桶挑戰(zhàn)賽”，要求參與者在網絡上發(fā)布自己被冰水澆遍全身的視頻內容，然后該參與者便可以要求其他人(規(guī)則為3個人)來參與這一活動。活動規(guī)定，被邀請者要么在24小時內接受挑戰(zhàn)，要么選擇為對抗“肌肉萎縮性側索硬化癥”捐出100美元。而事件發(fā)展到后來活動者不僅接受挑戰(zhàn)并且也捐出善款。2014年8月中旬，冰桶挑戰(zhàn)賽活動蔓延至中國，多名科技界、演藝界及體育界名人被點名參與了這一活動。如率先完成挑戰(zhàn)的一加手機創(chuàng)始人劉作虎，同時點名奇虎360 CEO周鴻祎、錘子科技CEO羅永浩、華為榮耀業(yè)務部總裁劉江峰參與該挑戰(zhàn)。基于這一活動規(guī)則，由發(fā)起挑戰(zhàn)者點名接力，然后這樣傳下去，這樣就形成了一個社交網絡。

本文主要基于新浪微博這一社交網站，搜集了2014年8月17日00:00點—8月22日24:00，6天的冰桶挑戰(zhàn)者的數據，挑戰(zhàn)者都會將視頻上傳到微博及相關社交網站，并在網站中點名其他人參與。基于此，搜集了參與挑戰(zhàn)者的相關信息包括自愿挑戰(zhàn)者(即沒被別人點名，自愿加入該活動的人)——自動加入網絡的節(jié)點，他們接受挑戰(zhàn)的時間(上傳視頻的時間)以及他點名的挑戰(zhàn)者，接下來被點名的人接受挑戰(zhàn)的時間及他點名的人。共搜集了6天786名挑戰(zhàn)者及他們的挑戰(zhàn)關系的數據。

1.2網絡構建

本文以天為劃分單位，分別構建了17日—22日6天的“冰桶挑戰(zhàn)”網絡。每個挑戰(zhàn)者作為網絡中的一個節(jié)點，點名關系用網絡連邊表示。為了便于觀察每天參與者的變化情況，本文把將挑戰(zhàn)者的關系統一編號，賦予不同的灰度，如圖1所示，不同灰度表示不同時間(以天為劃分單位)的網絡節(jié)點(由內到外時間依次增加)。從圖1可以發(fā)現隨著時間變化，挑戰(zhàn)者數量不斷增加，相應的網絡不斷擴大。接下來分析具體網絡結構的演化的過程。

2網絡的演化特性

首先分析網絡每天的結構及其演化過程，圖2展示了該網絡的演化過程。

從圖2可以直觀看出該網絡的演化過程中的一些特點：開始時節(jié)點較少，即事件發(fā)生初期參與挑戰(zhàn)的人較少，接著有節(jié)點緩慢增加的過程，而后受到社交媒體的影響，參與者越來越多，網絡節(jié)點急劇增加到后面網絡演化已不可控制。該過程類似于在線社會網絡上的信息傳播，信息如果按照既定規(guī)則來，就會以某一節(jié)點為中心散發(fā)。然而從圖中觀察發(fā)現，在第1天有“劉作虎”、“古永鏘”和“葉丙成”3人加入網絡，并且“葉丙成”只點了兩個人并沒有遵循既定規(guī)則，所以網絡的演化并不會像既定規(guī)則那樣發(fā)展。網絡形成時的狀態(tài)對于以后的網絡演化有重要的影響，到了第2天自動加入網絡的節(jié)點變得更多，這些節(jié)點增加也沒有一定的規(guī)則，是隨機加入到網絡的，因此網絡呈現不規(guī)律的增長。在實際社交網絡中，有些參與者會破壞既定規(guī)則——有的自動加入到網絡，有的點名不是3人，導致網絡的演化沒有一定的規(guī)律，這也是現實社交網絡難以用現有理論模型擬合的主要原因。

2.1理論模型

根據“冰桶挑戰(zhàn)”網絡的演化規(guī)則，本文建立一個簡單的理論模型與實際情況對比分析，理論模型如下：

2.2網絡規(guī)模

網絡規(guī)模的變化體現整個網絡的演化特征，本文從網絡的節(jié)點數、邊數及每個網絡新增節(jié)點數的角度與理論模型對比分析，如圖3所示。

由圖3a與b可以看出網絡規(guī)模不斷擴大，開始時節(jié)點增加緩慢，接著急劇增加，到第5天第6天節(jié)點增加緩慢。同樣，網絡中邊的數量也不斷增加，開始時由于參加者較少，邊數增加緩慢，到第3第4第5天時由于節(jié)點數顯著增加，邊數也急速增加，而最后一天增加變緩。對比分析，理論模型有些不同：在開始階段網絡中節(jié)點數和邊數增加緩慢，到第5天第6天時增加迅速，與實際情況差別較大。因為實際社交網絡的演化受一些人的主觀因素及外界客觀因素的影響，理論模型并沒有考慮這些因素。接下來，分析網絡每天新增加節(jié)點數的變化。

從圖3c可知，在網絡形成初期網絡每天實際新增加節(jié)點數從14到48到141再到224迅速增加，相比理論模型的指數式增長快。分析原因：一方面由于很多人打破了既定規(guī)則，另一方面由于社交媒體的顯著影響使得人們得到紛紛響應。這也說明在該網絡生成與演化過程中，由于受其他因素的影響，現有的理論模型并不適用于類似社交網絡的演化。而第5第6天網絡的新增節(jié)點數由226變?yōu)榱?33，增加變緩并且有所下降，說明這一事件過了一定的熱度，相應地參與者變少；另一方面觀察數據發(fā)現在第5天和第6天加入的用戶，在社交網絡上一般為普通用戶，粉絲量較少不會被社交媒體關注，大都不會在社交網絡上發(fā)布相關信息，因此該網絡就會在這些節(jié)點停止演化。

2.3網絡的拓撲結構演化分析

分析了網絡規(guī)模的變化，接下來具體分析網絡結構特性是如何演化的。由于“冰桶挑戰(zhàn)”規(guī)則所限，大家大都會點名自己的親密朋友(強關系)參加挑戰(zhàn)，體現在網絡中邊的方向只表示先后點名關系。在實際社交中他們互為朋友關系，體現在網絡中即為雙向關系。因此本文在計算網絡指標時將該網絡看成無向網絡。

2.3.1網絡密度

一個包含N個節(jié)點的網絡的密度ρ定義為網絡中實際存在的邊數M與最大可能的邊數之比。因此，對于無向網絡有從圖4a可以看出，該網絡密度逐漸變小。網絡節(jié)點的增加，雖然網絡中邊也增加，但兩者不是同比例變化的，對于整個網絡來說逐漸變得稀疏。

(1)

圖4b為文獻[11]研究Yahoo!360這一社交網絡的密度演化。所用的數據是從該網站開始建立到第40周的數據。從圖4b可以發(fā)現：網絡有3個清晰的階段：起初增加到一個峰值然后開始減小，最后逐漸穩(wěn)步增加。文獻解釋了其中的原因：社交網絡建立后，存在少數對該網絡有好奇心的人加入，并瘋狂地邀請許多朋友來加入體驗，這引起了第一個階段的高峰期。第二階段對應于這種新鮮感自然衰減，導致網絡密度的下降。第三階段對應于網絡真正的有機增長(當越來越多的人知道了該網絡時)。越來越多的人加入該網絡，節(jié)點和邊的增加最終使得密度穩(wěn)步上升。對比圖4a圖4b，“冰桶挑戰(zhàn)”網絡的密度并沒有出現圖4b的3個階段，并且最大值也就達到0.12左右，而Yahoo!360網絡的密度最大達到0.9多，最小的也在0.3左右。分析其中的原因：“冰桶挑戰(zhàn)”網絡的密度并沒有增加，原因是該網絡是點名親密好友關系的網絡，不是所有好友，邊數增加是有限的，所以網絡密度不會增加。然而Yahoo!360網絡節(jié)點之間的關系是非常稠密的，因為用戶可以邀請他所有的朋友加入，但是其中的強關系是非常稀少的。

2.3.2聚類系數

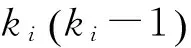
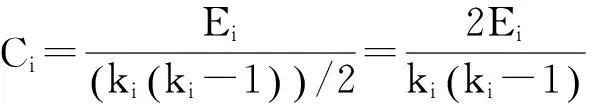
(2)

其中，Ei為節(jié)點i的ki個鄰居節(jié)點之間事實存在的邊數。

在一個網絡中，聚類系數是衡量網絡中一個節(jié)點的鄰居間緊密程度的一個指標，用來考察節(jié)點及其鄰居所呈現出來的結構。大多數真實網絡比如Facebook、Twitter、人人網及新浪微博等都表現出聚集結構。

本文計算出網絡前6天的平均聚類系數，如圖5所示。

從圖5a中不難發(fā)現，聚類系數在前兩天為0，接著迅速增加，到后面又開始減小。分析其中的原因：可以看出網絡在形成初期，并沒有形成三角關系，而是類似于星型結構，發(fā)散出去。如果按照既定規(guī)則演化網絡的聚類系數會一直為0，節(jié)點不會出現三角關系。然而該網絡演化到一定程度，在第3天時聚類系數變?yōu)?.016 7并且開始增加，網絡出現了三角關系，意味著實際網絡出現了共同好友關系。在現實中，由于人際關系的影響人的親密朋友可能不止一個，在信息傳播過程中由于獲取信息不及時等原因，被多個好友點名的情況就會發(fā)生，所以隨著該網絡的演化，聚類系數就變?yōu)榉橇阒怠＞W絡節(jié)點在增加的同時，整個網絡中挑戰(zhàn)者間彼此成為好友的機率也增加導致聚類系數不斷增加。而后平均聚類系數有所減小，說明網絡擴展速度變快，網絡變得發(fā)散，導致網絡的平均聚類系數減小。

Bimal Viswanath研究了Facebook這一社交網絡的演化。搜集到的數據為2006年9月至2009年1月的數據。圖5b為文獻[14]中Facebook社交網絡的聚類系數演化過程。橫坐標表示2007年及2008年不同的月份。從圖中不難發(fā)現，Facebook網絡的聚類系數平均在0.13左右。然而，本文研究的網絡集聚系數最大達到0.02左右，要比Facebook網絡小的多。分析其中的原因：首先Facebook網絡的數據是網絡誕生后中間時間段的數據，而在網絡中朋友間一旦建立好友關系，就不會有很大變動。本文網絡聚類系數具有明顯的變化，是因為在網絡形成初期，朋友關系會因為節(jié)點的不斷加入而發(fā)生變化。其次，Facebook網絡考慮了用戶的所有關系，本文的網絡只有強關系，所以聚類系數相對較小。

2.3.3網絡效率與最大連通子圖

網絡中兩個節(jié)點i和節(jié)點j之間的最短路徑是指連接著兩個節(jié)點的邊數最少的路徑。兩點間的距離dij定義為連接著兩個節(jié)點的最短路徑上的邊的數目。對于不連通的網絡，可能兩個節(jié)點之間不存在連通的路徑，即意味著這兩個節(jié)點之間的距離為無窮大，從而導致整個網絡的平均路徑也為無窮大。為了避免這種情況，定義一個網絡的平均效率[15]：

(3)

其中,N為網絡中節(jié)點個數，dij為節(jié)點i到節(jié)點j的距離。兩個點之間的距離越短那么兩點之間信息傳遞的效率則越高，即效率與兩點距離成反比關系。

網絡的連通子圖體現了一個網絡的連通比率，對于分析信息在網絡中的傳播有重要的作用，研究網絡動態(tài)演化有著重要的意義。本文計算得到了6個網絡的效率如圖6a所示及每個網絡的子圖數量和最大連通子圖節(jié)點的個數，如圖6c～d所示。

根據網絡效率的定義也可以看出網絡效率受到網絡子圖個數的影響，當網絡中子圖較多時網絡效率就會變小。具體分析，從圖6a中可以發(fā)現前3個網絡的效率由開始的0.214 3變?yōu)?.058 8又到0.039 9逐漸變小，且第2個網絡比初始網絡減小了81.4%。開始時網絡的節(jié)點數較少，不連通子圖數量也較少，節(jié)點間相互達到的路徑很短，因此網絡效率較高。隨著新節(jié)點的不斷加入，不連通子網不斷增加導致節(jié)點間的路徑變得較大，網絡效率變小。隨后網絡效率從0.098 9到0.125 9變大，隨著網絡的不斷擴大，網絡的密度變大因此效率就會增加。最后又有減小趨勢到0.121 8，同樣也受到網絡規(guī)模的影響，節(jié)點間的路徑變長。同樣，圖6b為文獻[14]中Facebook社交網絡的平均路徑長度演化過程。從圖不難發(fā)現，Facebook網絡節(jié)點間的平均最短路徑在7左右不會有很大變化，而本文網絡效率到最后也趨于穩(wěn)定在0.12左右。分析兩者異同的原因：當網絡演化到一定程度時，網絡中每個節(jié)點的連邊基本不會發(fā)生太大變化，使得網絡效率或者最短路徑趨于穩(wěn)定。而本文網絡由于節(jié)點連接邊較少、連通子圖數量較多等原因使得網絡效率較低。

觀察圖6a與圖6b不難發(fā)現，網絡效率與連通子圖數有很大相關性。即網絡效率下降時網絡子圖數量增加，當網絡效率上升時，網絡子圖數量減小，說明網絡子圖數量影響網絡效率的變化。從圖6b中網絡子圖數量的演化可知，在網絡形成初期網絡子圖數量迅速增加，由3變?yōu)?0到18，說明該事件能夠得到很多人的響應，自愿加入到網絡中。而后又有減小的趨勢，說明網絡連通性變好，一方面說明自愿挑戰(zhàn)者的數量減小，另一方面可能是很多獨立網絡連接到了一起，在現實中朋友關系更加密切。從圖6c也不難發(fā)現最大連通子圖的節(jié)點數量不斷增加，說明很多獨立子網絡很快融入到最大子網絡里，形成一個連通網絡。

3總結與展望

社交網絡的形成與演化從一定程度上來講是人際關系的不斷延伸，是一個復雜的過程，現實的和虛擬的各種因素相互影響，呈現多種特征。

本文主要從“冰桶挑戰(zhàn)”這一事件出發(fā)，構造了一個真實的社交網絡。搜集從網絡形成到第六天的數據，從網絡規(guī)模等研究了該網絡的演化過程。通過分析發(fā)現該網絡密度不斷減小；聚類系數從初始值零增加到0.016 7后又緩慢減小；網絡效率從0.214 3開始減小，最大減小量為初始值的81.4%，后又緩慢增加；連通子圖的數量從3迅速增加，最高增加了初始值的5倍，后又減小。本文發(fā)現連通子圖的數量與網絡效率呈負相關關系。從這些結論中，可以清楚看出這一特殊網絡的演化過程，為社交網絡演化模型的建立提供一定依據。本文也與其他大型社交網絡的演化做了對比分析，從中也可以得出本文社交網絡演化的特殊性。

對于包括社交網絡在內的復雜網絡而言，結構與演化動力學的研究正逐漸成為熱點。復雜網絡的研究重點也逐漸轉向基于結構的信息傳播演化過程。只有理解了在這種結構上的傳播機理后，才能夠有根據地進行傳播的控制問題研究。在現實世界中，一些事件的發(fā)展社會媒體起到了很大的作用，而如何量化社交媒體的作用也是一個亟待解決的問題。本文在獲取“冰桶挑戰(zhàn)”數據的過程中，只搜集一些名人的數據，對于很多參與挑戰(zhàn)的普通人并沒有考慮在內，這樣難免會影響到網絡的演化過程。另外，對于在統計數據時由于有時間差有些數據難免會有所遺漏，從一定程度上影響了結論的精確度。

參考文獻:

[1]斯坦利·沃瑟曼，凱瑟琳·福斯特. 社會網絡分析: 方法與應用[M]. 陳禹，孫彩虹,譯. 北京: 中國人民大學出版社, 2012.

[2]Dodds P S, Muhamad R, Watts D J. An experimental study of search in global social networks[J]. Science, 2003, 301(5634): 827-829.

[3]Shin D H. The effects of trust, security and privacy in social networking: a security-based approach to understand the pattern of adoption[J]. Interacting with Computers, 2010, 22(5): 428-438.

[4]MisloveA, Marcon M, Gummadi K P, et al. Measurement and analysis of online social networks[C]//Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement. ACM, 2007: 29-42.

[5]Hellmann T, Staudigl M. Evolution of social networks[J]. European Journal of Operational Research, 2014, 234(3): 583-596.

[6]Watts D J, Strogatz S H. Collective dynamics of ‘small-world’networks[J]. Nature, 1998, 393(6684): 440-442.

[7]Newman M E J, Watts D J. Renormalization group analysis of the small-world network model[J]. Physics Letters A, 1999, 263(4): 341-346.

[8]Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.

[9]張立, 劉云. 虛擬社區(qū)網絡的演化過程研究[J]. 物理學報, 2008, 57(9): 5419-5424.

Zhang L, Liu Y. Research on the evolution process of virtual community networks[J].Acta Physica Sinica, 2008, 57(9): 5419-5424.

[10] 熊熙,曹偉, 周欣, 等. 社交網絡形成和演化的特征模型研究[J]. 四川大學學報: 工程科學版, 2012, 44(004): 140-144.

Xiong X, Cao W, Zhou X, etal. Research on the feature model of the formation and evolution of social networks[J]. Journal of SichuanUniversity(Engineering Science Edition), 2012, 44(004): 140-144.

[11] Kumar R, Novak J, Tomkins A. Structure and evolution of online social networks[M]//Link Mining: Models, Algorithms, and Applications. Springer New York, 2010: 337-357.

[12] 郭海霞. 新型社交網絡信息傳播特點和模型分析[J]. 現代情報, 2012, 32(1): 56-59.

GuoHaixia. New Social networking features andmodel analysis of information dissemination[J]. Journal of Modern Information, 2012, 32(1): 56-59.

[13] 汪小帆,李翔,陳關榮.網絡科學導論[M].北京:高等教育出版社,2012.

[14] Viswanath B, Mislove A, Cha M, et al. On the evolution of user interaction in Facebook[C]//Proceedings of the 2nd ACM Workshop on Online Social Networks. ACM, 2009: 37-42.

[15] Latora V, Marchiori M. Efficient behavior of small-world networks[J]. Physical Review Letters, 2001, 87(19): 198701.

(責任編輯李進)

The Evolution of Social Networks Constructed by “Ice Bucket Challenge”

YANG Kai, LIU Xiaolu, LIN Jianhong, CHENG Xi, GUO Qiang, LIU Jianguo

(Research Center of Complex Systems Science, University of Shanghai for Science and Technology, Shanghai 200093)

Abstract：The evolutionary process of social networks at initial period is very important, especially for the quantitative understanding of the formation and the evolution of interpersonal relationships. In this paper, combining with the “Ice Bucket Challenge”, we collect the data of this event from the launch to the sixth day in our country. The nodes stand for the challengers and the edges are the relations of called people in the social networks. By analyzing the rules of the structural characteristics, including the network size, the clustering coefficient, density, network efficiency and connectivity sub-graphs, we find that the clustering coefficient increased from zero to 0.0167 at the beginning and then decreases; the densityof the network declines from 0.1209 over time; the network efficiency reduces by 81.4% at first and then slowly increases; the connected sub-graphs rapidly increases five times and then decreases; the network efficiency and the number of sub-graphs are negatively correlative. Taking into account the specificity of the network,we compare with evolution of other social networks.Thiswork will be helpful for understanding the law of the formation and development of the early social networks.

Key words：social networks; network evolution; topological structure; Ice Bucket Challenge

文章編號：1672—3813(2016)02—0090—07;

DOI:10.13306/j.1672-3813.2016.02.011

收稿日期：2014-10-29；修回日期：2015-01-12

基金項目：國家自然科學基金(71171136，61374177，71371125)；上海市一流學科建設項目(XTKX2012)；教育部人文社科基金(13YJA630023)；上海出版?zhèn)髅窖芯吭洪_放基金(SAYB1407)

作者簡介：楊凱(1987-)，男，山東泰安人，博士研究生，主要研究方向為在線社會網絡結構與演化分析。 通訊作者：劉建國(1979-)，男，山西臨汾人，教授，主要研究方向為網絡科學，商務智能，知識管理。

中圖分類號：N941

文獻標識碼：A