一種高精度的大點數二維FFT處理器設計

于　東，李　麗，韓　峰，王　堃，豐　帆，潘紅兵

(南京大學 電子科學與工程學院,　南京 210046)

?

·信號處理·

一種高精度的大點數二維FFT處理器設計

于東，李麗，韓峰，王堃，豐帆，潘紅兵

(南京大學 電子科學與工程學院,南京 210046)

摘要：基于傳統的頻域抽取快速傅里葉變換(FFT)算法以及二維FFT算法，設計了一種高精度的大點數FFT處理器。該處理單元采用一個狀態機控制整個運算流程，針對小點數情況的一維FFT算法和大點數情況的二維FFT算法，該處理器都可以智能地選擇合適的處理流程和緩存管理，自動地完成整個FFT運算而無需軟件介入。在支持大點數的二維FFT算法的基礎上，該設計還通過對旋轉因子計算過程的優化，以提高在大點數情況下的精度表現，在4M長度的輸入序列時可以獲得130 dB以上的信噪比。

關鍵詞：快速傅里葉變換；二維快速傅里葉算法；高精度；大點數；旋轉因子優化

0引言

快速傅里葉變換(FFT)是信號處理領域一種重要的快速變換方法，自幾十年前Cooley和Tukey[1]提出FFT至今，這一算法日趨成熟，并衍生出多種新的形式，但主要可以歸納為兩個發展方向，一是針對2的整數次冪的算法，如：基2算法、基4算法[2]和分裂基算法[3]等;另一個是N不等于2 的整數次冪的算法，如：素因子算法和Winograd算法。隨著計算機軟件技術和超大規模集成電路(VLSI)的發展，如今我們可以非常方便地使用軟件實現FFT，在速度要求更高的領域，需要通過電路來實現這一算法[4]。

鑒于FFT本身的特點，通過電路實現存在一些難點，譬如如何用同一套電路實現不同長度輸入序列的FFT，運算速度和精度如何保證等等。事實上，通過ASIC來實現某種特定的算法，雖然可以達到較高的性能，但通常會存在諸如緩存容量方面的限制[5]，如何權衡性能和硬件資源，這是一個電路設計者必須深入思考的問題。綜上所述，本文所設計的FFT處理器具有如下特點：

(1)支持16 M～4 M任意長度輸入序列；

(2)支持二維FFT算法，對于緩存無法一次容納的輸入數據量，通過二維FFT算法完成運算；

(3)對緩存的管理非常靈活，小點數情況下，輸入數據可以存放在緩存的任意位置，并且可以通過乒乓操作同時進行多個輸入序列的計算，大點數情況下，可以通過乒乓操作將運算時間隱藏入數據傳輸時間中；

(4)運算精度高，通過對旋轉因子計算過程的優化，信噪比可以達到130 dB以上。

1基8和二維FFT算法簡述

首先，N點序列x(n)，其FFT定義為

(1)

本設計中，緩存為2 MB。對于長度小于等于256 k的輸入序列，緩存可以一次容納，因此屬于小點數的范圍；對于長度大于256 k的輸入序列，屬于大點數范圍，需要引入二維FFT算法進行運算。

對于小點數情況，本設計采用傳統的頻域抽取的基8算法，對于不滿足2n的點數，需要補零。

對于頻域抽取的基8算法[6-7]，將頻域X(k)的序號按除以8的余數分開。按照式(1)，先將x(n)按序號分為8個部分，得

(2)

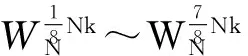
令R8(0)～R8(7)分別表示R8矩陣的第一行至第八行，這樣，上述八個表達式可簡潔地表示為

(3)

根據式(3)，可以推導出頻域抽取的基8-FFT算法的蝶形運算過程，如圖1所示。

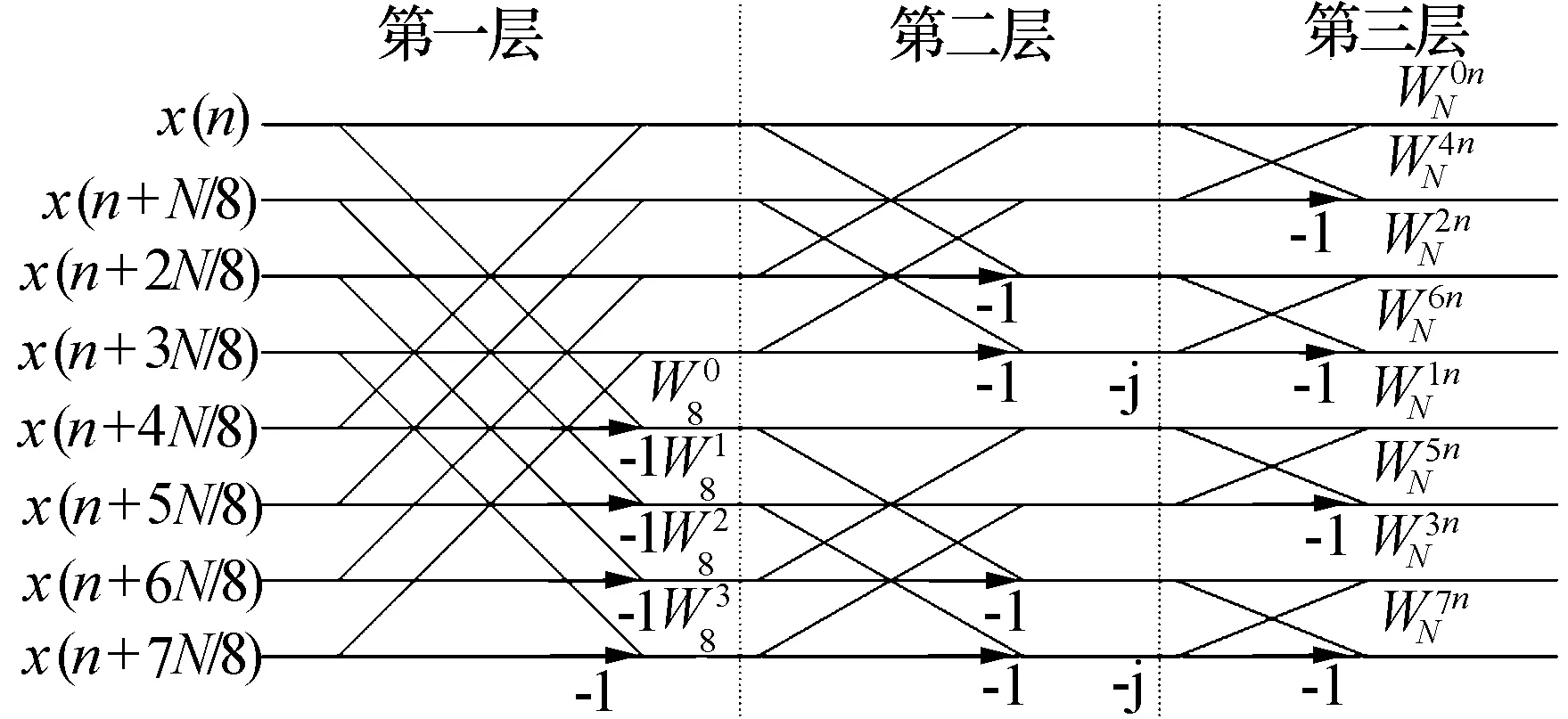
圖1　頻域抽取的基8-FFT算法蝶形單元

對于大點數情況，本設計采用傳統常見的二維FFT算法[8]。設長度為N的輸入序列x(n)，設置常量N1、N2，使得

(4)

其中

這樣，原始的FFT公式可以按照式(5)形式進行變化

X(k)=X(k1+N1k2)=

(5)

根據對式(5)的理解，我們可以將初始的較長的輸入序列劃分為一個矩陣，其行數和列數分別為N1和N2，如式(6)所示

(6)

將式(5)運用到式(6)的矩陣上，可以分解為三步：

(1)對矩陣的每一列做FFT運算；

(3)對矩陣的每一行做FFT運算。

2運算流程和狀態機設計

FFT處理器硬件實現的架構如圖2所示。主要功能單元包括控制單元、地址單元、蝶形單元、旋轉因子生成單元、乘法單元等[9]。控制單元采用狀態機實現，通過向其他功能模塊發送相應的控制信號來控制整個運算的流程。但是對于小點數和大點數兩種不同情形，運算的流程也會有所不同，具體來講，可以對應到控制單元中狀態機不同的狀態跳轉流程。

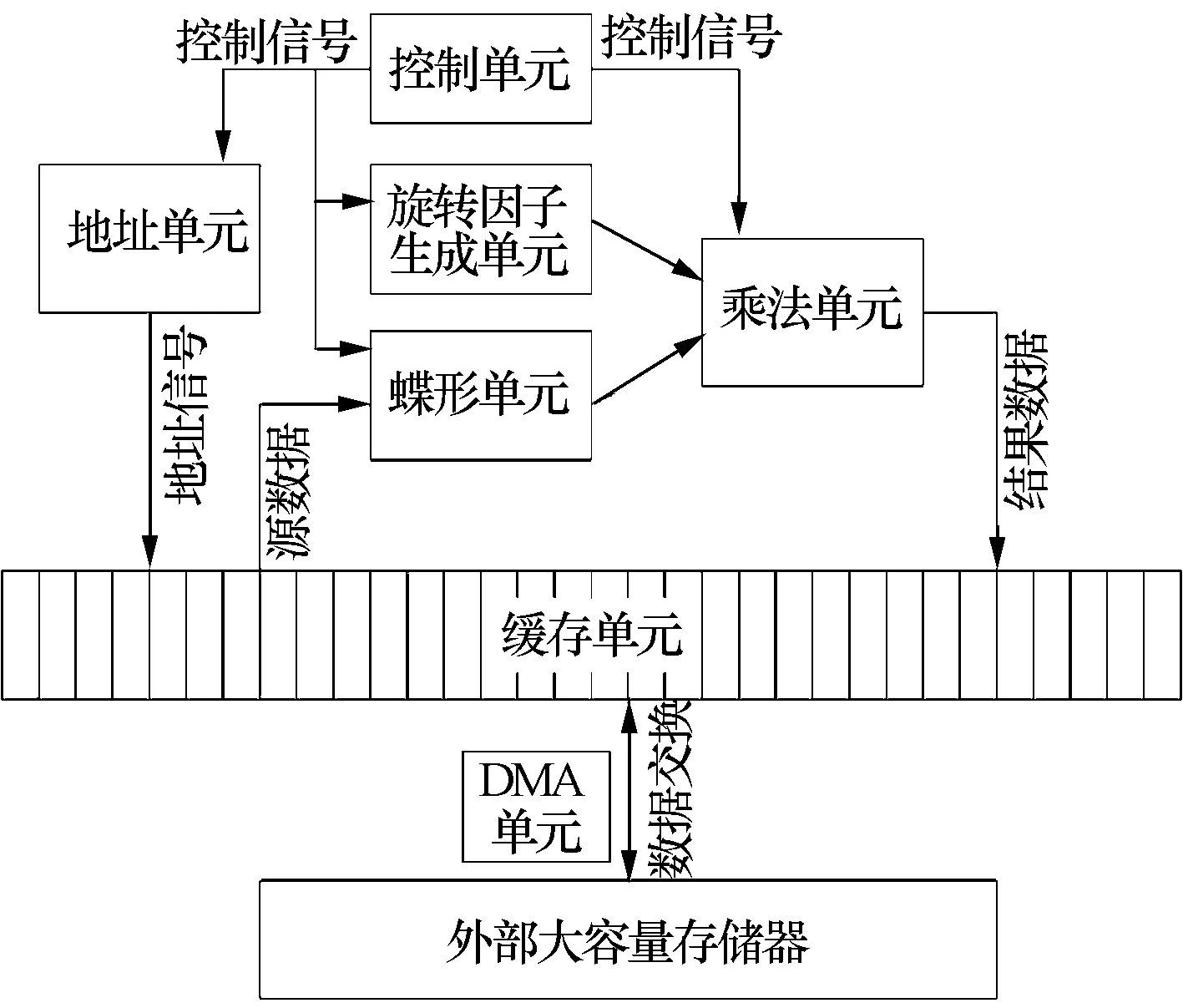
圖2　FFT處理器實現架構

FFT處理器中，2 MB緩存被劃分成32個bank。通過這樣的劃分，控制單元可以通過與DMA單元的配合實現對緩存的靈活調度，從而完成乒乓操作[10]。對于小點數情形，運算過程僅需占用其中的16個bank，當數據從外部大容量存儲器搬入緩存單元的16個bank后，控制單元開始啟動運算單元進行運算，在運算的同時，控制另一組數據從外部大容量存儲器搬入緩存單元的另外16個bank，前一個運算完成后，控制單元可以調度運算單元直接進入運算過程，無需再等待數據的搬入，從而大幅提高了小點數情形的運算速度。

對于大點數情形，由于緩存無法一次容納所有的數據，必須分段地進行計算，這就產生了多次緩存與外部存儲器之間的數據交換過程，通過乒乓操作，同樣可以大幅提高大點數FFT的運算性能。

為了實現完整的FFT運算過程，并支持大點數情況下的二維FFT算法，控制單元的狀態設計機如圖3所示。

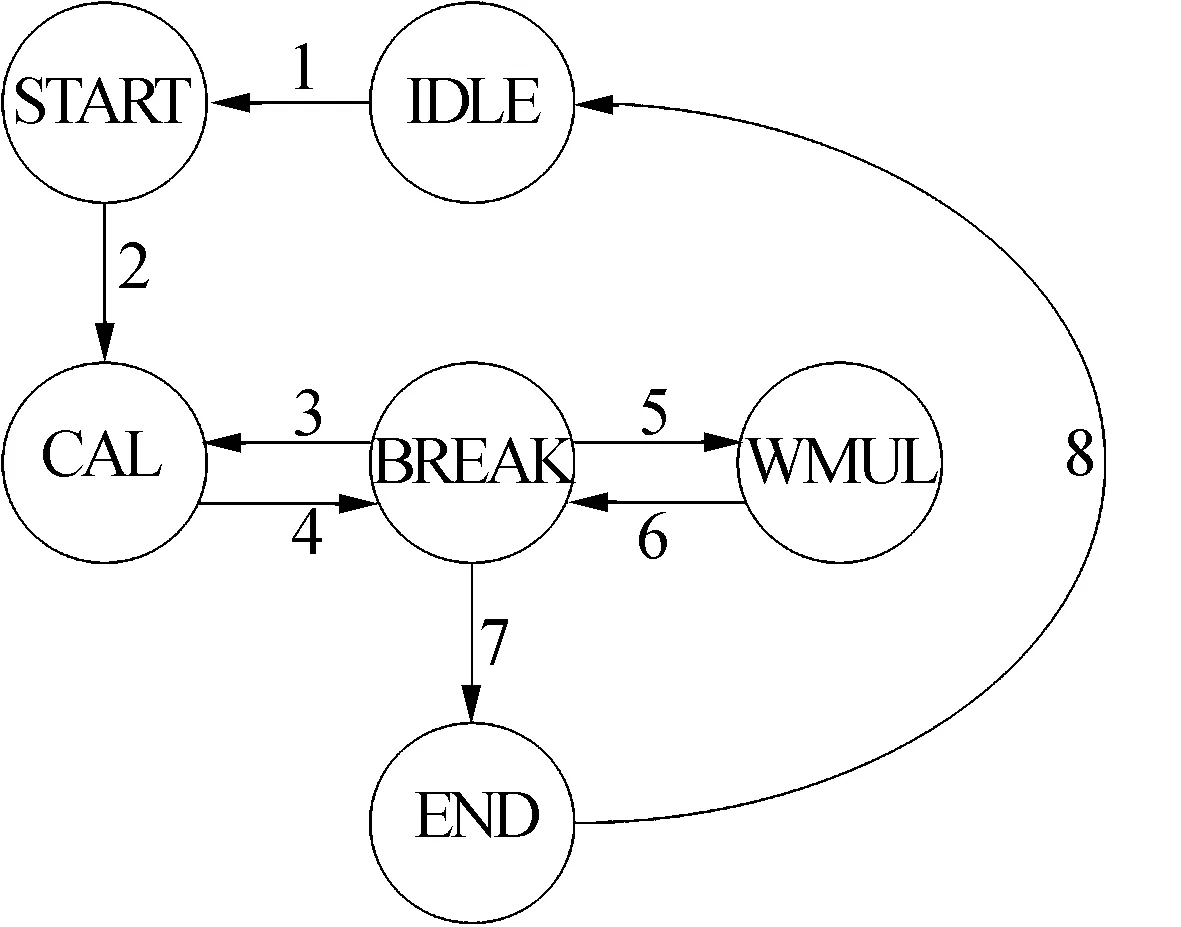
圖3　FFT處理器控制單元狀態轉移圖

對于小點數情形(以4 k點為例)，運算流程和狀態跳轉如下：

(1)狀態機初始處于IDLE狀態，數據從外部大容量存儲器傳輸到緩存單元；

(2)運算開始，狀態跳轉至START(路徑1)；

(3)開始第一級運算，狀態跳轉至CAL(路徑2)，源數據從緩存單元流入蝶形單元進行基8運算，旋轉因子生成單元通過計算生成旋轉因子，蝶形單元計算結果與旋轉因子匯入乘法單元進行相乘運算，結果數據返回緩存單元；

(4)第一級運算完成，狀態跳轉至BREAK(路徑4)；當第一級的結果數據返回緩存單元后，進入第二級運算，狀態重新跳轉至CAL(路徑3)；

(5)相似地進行第二、三、四級運算(因為4 k=84，共需要4級運算)，狀態跳轉至BREAK(路徑4)，此時所有運算結束，狀態跳轉至END(路徑7)；

(6)給出運算完成的結束信號，狀態重新跳轉至IDLE(路徑8)，最終的運算結果數據從緩存單元傳輸到外部大容量存儲器。

對于大點數情形(以4 M點為例)，運算流程和狀態跳轉更為復雜[11]，如下：

(1)4M數據存在于外部大容量存儲器中，我們可將其視為一個1 k×4 k的源數據矩陣S；

(2)將矩陣S每一行的第0～127個數據搬入緩存單元，并在搬運過程中，通過DMA單元使數據在緩存中排布成128個長度為1 k的序列形式，在此過程中，共傳輸128 k數據量，剛好占滿緩存單元的第0～15個bank；

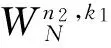
(4)類似于步驟(3)，完成剩余的127個長度為1 k的序列的運算，在運算的同時，按照類似于步驟(2)的過程，將矩陣S每一行的第128～255個數據搬入緩存單元的第16～31個bank；

(5)當運算和數據傳輸完成后，控制單元直接開始第16～31個bank中數據的運算，同時，將第0～15個bank中的中間結果數據傳送至外部存儲器，并將矩陣S每一行的第256～383個數據搬入緩存單元的第0～15個bank；

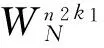
(7)將矩陣M的前32行存入緩存單元，并在傳輸過程中，通過DMA單元使數據在緩存中排布成32個長度為4 k的序列的形式，在此過程中，共傳輸128 k的數據量，剛好占滿緩存單元的第0～15個bank；

(8)按照小點數情形的運算流程完成這32個4 k長度的FFT運算，在運算的同時，按照類似于步驟(7)的過程，將矩陣M的第32～63行數據存入緩存單元的第16～31個bank；

(9)當運算和數據搬運完成后，控制單元直接開始第16～31個bank中數據的運算，同時，將第0～15個bank中的中間結果數據傳送至外部存儲器，并將矩陣M的第64～95行數據存入緩存單元的第0～15個bank；

(10)將上述的步驟(8)至步驟(9)重復32次，這就完成了對矩陣M每一行的FFT運算，得到了最終的4 M長度序列的FFT結果。

通過上述設計，可以使同一個狀態機兼容小點數和大點數的運算流程。另外，通過與DMA模塊的配合以及劃分為32 bank的緩存模塊設計，可以實現數據搬運過程與計算過程的并行，提高了FFT處理器的性能，具體的性能提升分析將在第4節中詳述。

3旋轉因子的實時計算及優化

出于節省運算資源的考慮，本設計當中采用單精度運算單元，由此帶來的問題是當輸入序列的長度較長時，FFT的運算精度就成為了一個無法忽視的問題。而旋轉因子的精度對最終結果的精度有著很大的影響，這是由于存儲空間的限制，我們不可能將所有的旋轉因子預先計算完成并存儲下來。因此，旋轉因子的生成一般考慮預先存儲少量的常數，然后通過實時計算得到[12]。本設計對常數的選擇和實時計算的方法進行了優化，在消耗極為有限的存儲空間(16 kB)的情況下，大幅提高了最終結果的運算精度，并同時兼容了不同輸入序列長度的旋轉因子生成要求。

圖4是本設計所采用的旋轉因子生成單元結構圖，其中，WSRAM_1和WSRAM_2用來存儲常數，每塊容量為8 kB，分別可以容納1 k個64 bit位寬的單精度復數。w_unit模塊用于實時計算旋轉因子，其主體為1個復數乘法器[13-14]，另外還包括一些地址生成邏輯和對稱性處理邏輯用來生成取數地址以及按照對稱性對計算結果做相應的處理。

圖4　旋轉因子生成單元結構圖

在此給出旋轉因子生成單元的整個工作流程：首先，w_unit根據當前輸入序列的長度生成相應的取數地址序列，并按照該地址序列從兩個常數存儲器WSRAM_1和WSRAM_2中取出對應的常數；然后，將這兩個常數傳回w_unit模塊并通過復數乘法器相乘，得出的乘積根據對稱性的需要進行相應的處理；最后，經由w_unit模塊輸出得到旋轉因子序列。

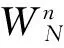
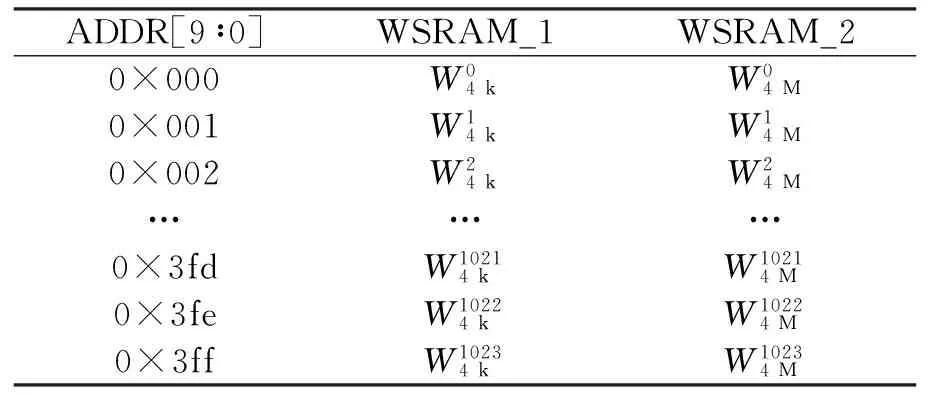
表1　常數存儲器WSRAM_1和WSRAM_2中的數據存儲形式

在取數過程中，為了得到地址序列，需要將n參數和k參數相乘，在w_unit中可以通過對n參數的移位和加法操作得到結果。這里稱n參數和k參數的乘積為kn參數(需要22bit位寬表示)。對于不同的輸入序列長度N，取數地址如表2所示。

表2　kn參數在不同輸入序列長度N下對應的取數地址

上述地址的產生依賴于FFT旋轉因子的一種屬性：旋轉因子具有很大的相關性，較小的輸入序列長度所需的旋轉因子往往包含在較大輸入序列長度所需的旋轉因子當中。

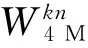
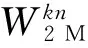
4FFT運算性能和精度分析

本設計使用Sysnopsis公司的VCS仿真工具，基于UVM驗證方法學進行了功能仿真，所有功能均順利通過。根據Design Compiler在TSMC_40nm工藝下綜合的結果，本設計可以運行在1 GHz的頻率以上。

對于運算性能的分析，本文使用周期數表示。對于任意2n點數，可以將其表示為2a×4b×8c形式，令其中的c盡可能大，則a和b最多有1個等于1或全為0。因此，該點數FFT運算的級數即為a+b+c。每一級的運算時間依賴于點數和運算單元的數量，在本設計中，運算單元的數量可以達到每周期2個數據的吞吐率，此時，每一級的運算時間為2n-1個周期。狀態機每次BREAK狀態均會消耗128個周期，共消耗(a+b+c-1)×128個周期。另外，運算的開始和結束時也需消耗一定的周期(137個)。因此，可以得到在2m條管線時完成2n點數的FFT所需的周期數為

T=137+(a+b+c-1)×128+

(a+b+c)×2n-1

(7)

但是上面的式(7)僅適用于小點數情況，對于大點數情況，運算完成的時間很大程度上需要依賴于外部存儲器和緩存單元之間的數據搬運時間。因為，通過對存儲器的乒乓操作，計算時間可以掩蓋在數據搬運時間當中。表3根據理論推導和VCS仿真結果給出一些典型點數下的運算周期數，512 k和1 M由于上述大點數的特殊性并沒有理論推導時間。

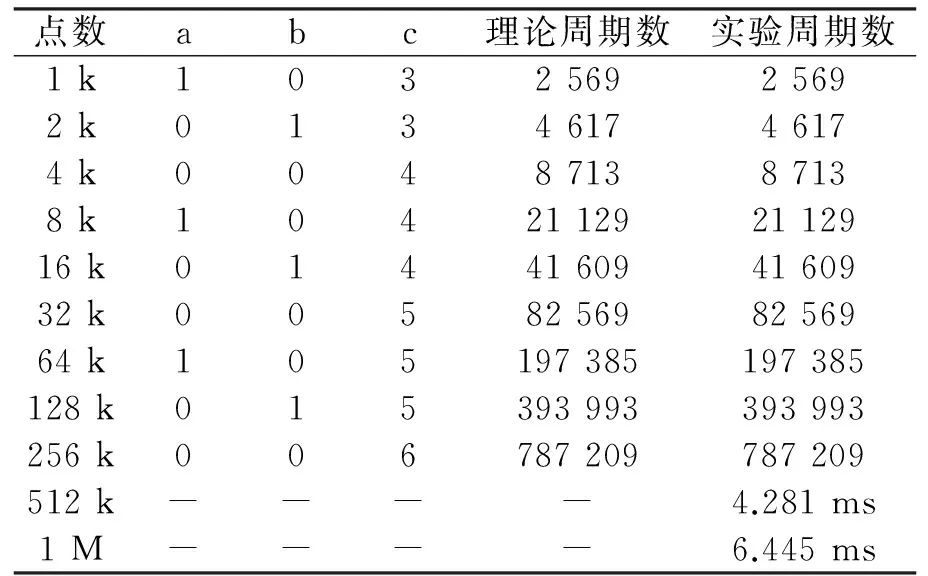
表3　1 k～1 M點數運算時間

對于運算精度的分析，本文采用matlab下雙精度運算結果作為參考，較大點數下得到的信噪比如表4所示。

表4　本設計在各點數情況下的信噪比

5結束語

FFT是數字信號處理中非常重要的算法。本文設計了一種高精度并支持大點數二維算法的FFT處理器，可以自動地完成小點數或大點數這2種情況下的整個FFT運算流程，并且對旋轉因子的存儲和計算過程進行了優化，使最終結果獲得了130 dB以上的信噪比。

參 考 文 獻

[1]胡廣書. 數字信號處理——理論、算法與實現[M]. 北京: 清華大學出版社, 1997.

HU Guangshu. Digital signal processing: theory, algorithm & implementation[M]. Beijing: Tsinghua University Press, 1997.

[2]王曉君, 龍騰, 周希元. 二維級聯流水結構大點數FFT運算器實現研究[J]. 無線電工程, 2010, 40(11): 19-22.

WANG Xiaojun, LONG Teng, ZHOU Xiyuan. Research on implementation of 2-dimension long FFT processor based on cascade-pipelined structure[J]. Radio Engineering, 2010, 40(11) : 19-22.

[3]林晗, 夏宇聞, 陳杰. 一種改進型基-8 FFT算法及其ASIC實現[J]. 中國集成電路, 2003(9): 68-71.

LIN Han, XIA Yuwen, CHEN Jie. An improved radix-8 FFT algorithm and ASIC implementation[J]. China Integrated Circuit, 2003(9): 68-71.

[4]陶而芳. 浮點FFT處理器IP設計[D]. 成都: 西南交通大學, 2008.

TAO Erfang. Design of float-point FFT processor IP[D]. Chengdu: Southwest Jiaotong University, 2008.

[5]陸波, 許煒陽, 胡星波, 等. 高吞吐率可配置FFT處理器IP核設計與VLSI實現[J]. 復旦學報(自然科學版), 2010, 49(2): 151-157.

LU Bo, XU Weiyang, HU Xingbo, et al. Design and VLSI implementation of IP core of high-throughput configurable FFT processor[J]. Journal of Fudan University(Natural Science) , 2010, 49(2): 151-157.

[6]賀衛東, 段哲民, 龔誠. 基于FPGA的大點數FFT算法研究[J]. 電子測量技術, 2007, 30(11): 14-16.

HE Weidong, DUAN Zhemin, GONG Cheng. 2D-parallel method for ultra long FFTs in FPGA[J]. Electronic Measurement Technology, 2007, 30(11): 14-16.

[7]蘇濤, 莊德靖.大點數FFT算法的改進及其實現[J]. 現代雷達, 2005, 27(7): 23-26.

SU Tao, ZHUANG Dejing. Improvement and implementation of FFT algorithm for long sequences[J]. Modern Radar, 2005, 27(7): 23-26.

[8]劉學梅, 孫志堅. 按頻率抽取的基4FFT算法在FPGA中實現[J]. 現代雷達, 2005, 27(1): 50-51.

LIU Xuemei, SUN Zhijian. Algorithmic realization of the radix-4 DIF FFT in FPGA[J]. Modern Radar, 2005, 27(1): 50-51.

[9]COOLEY J W, TURKEY J W. An algorithm for the machine computation of complex Fourier series[J]. Mathematics of Computation, 1965, 19(4): 297-301.

[10]MA Y, WANHAMMAR L. A hardware efficient control of memory addressing for high-performance FFT processors[J]. IEEE Transactions on Signal Processing, 2000,48(3): 342-345.

[11]STEVENSON D. 754-1985-IEEE standard for binary floating-point arithmetic[J]. IEEE Journal, 1987(4): 345-348.

[12]SIDDAMAL S V, BANAKAR R M, JINAGA B C. Design of high-speed floating point multiplier[C]// 4th IEEE International Symposium on Electronic Design, Test & Applications. [S.l.]: IEEE Press, 2008: 285-289.

[13]HORIMA Y, ONOMI T, KOBORI M, et al. Improved design for parallel multiplier based on phase-mode logic[J]. IEEE Transactions on Applied Superconductivity, 2003, 13(2): 527-530.

[14]GEORGE K, CHEN C I. Configurable and expandable FFT processor for wideband communication[C]// IEEE Instrumentation and Measurement Technology Conference. [S.l.]: IEEE Press, 2007: 1-6.

于東男，1990年生，碩士研究生。研究方向為VLSI設計。

韓峰男，1987年生，博士研究生。研究方向為VLSI設計和高性能計算架構。

李麗女，1975年生，教授，博士生導師。研究方向為VLSI設計、數字信號處理系統、可重構計算、多核SoC設計方法學。

A High-precision FFT Processor Supporting 2D FFT Algorithm

YU Dong，LI Li，HAN Feng, WANG Kun，FENG Fan，PAN Hongbing

(College of Electronic Science and Engineering, Nanjing University,Nanjing 210046, China)

Abstract：Based on the traditional DIF FFT and 2D FFT algorithm, a high-precision FFT processor supporting various input data size is designed. In the procedure of FFT calculation, a finite state machine is used as a controller. When the input data size varies in a range, the cache can be smartly managed and 1D/2D FFT algorithm is automatically chosen according to the situation whether the amount of input data is beyond the cache size. Therefore the whole FFT calculation can be completed without any involvement of software but a start signal. Other than the support to 2D FFT algorithm in case the cache is not enough, an optimization in the calculation procedure of twiddle factor is introduced to improve its precision and furtherly to improve the precision of final results when facing a large input data size. In the FPGA verification, a 130 dB or higher SNR(signal-noise ratio) is reached while the SNR is only around 110 dB without this optimization.

Key words：FFT; 2D FFT algorithm; high precision; large data size; optimization about twiddle factor

DOI：10.16592/ j.cnki.1004-7859.2016.05.005

基金項目：國家自然科學基金資助項目(61176024、61006018)；高等學校博士學科點專項科研基金資助項目(20120091110029)；江蘇省科技廳科技廳產學研聯合創新基金(BY2013072-05);江蘇高校優勢學科建設工程資助項目。

通信作者：于東Email：469889089@qq.com

收稿日期：2016-01-22

修訂日期：2016-03-21

中圖分類號：TN957

文獻標志碼：A

文章編號：1004-7859(2016)05-0016-06