自適應變阻尼控制算法在隨動系統中的應用

張文文，王建偉，侯　文

(1. 中北大學 儀器與電子學院,　太原 030051；　2. 南陽北方紅宇機電制造有限公司，　河南 南陽 474675) (3. 中北大學 信息與通信工程學院，　太原 030051)

?

·天饋伺系統·

自適應變阻尼控制算法在隨動系統中的應用

張文文1，王建偉2，侯文3

(1. 中北大學 儀器與電子學院,太原 030051；2. 南陽北方紅宇機電制造有限公司，河南 南陽 474675) (3. 中北大學 信息與通信工程學院，太原 030051)

摘要：為了提高電動舵機系統的動態響應性能，文中提出了一種自適應變阻尼控制方法。首先，在分析舵機傳遞函數的基礎上對其進行了簡化；其次，分析了無阻尼自然頻率和阻尼比對系統動態性能的影響；再次，結合常規PID控制結構簡單、易于實現和遺傳算法自適應能力強的優點，設計了基于自適應變阻尼控制算法的新型變阻尼控制器；最后，通過仿真結果對比，表明自適應變阻尼控制方法可以優化隨動系統的動態響應性能，系統單位階躍響應速度快，無超調。

關鍵詞：隨動系統；變阻尼控制；遺傳算法

0引言

隨動系統的輸入信號是變化規律不確定的任意時間函數，其主要任務是使被控制量按照輸入信號的變化而變化，并使輸出信號與輸入信號的誤差保持在要求指標范圍內。電動舵機是典型的位置隨動控制系統。相比于一般的隨動系統，電動舵機對系統快速性和準確性的要求更高，即要求系統響應時間更短，超調量更小。關于隨動系統控制方法的研究很多，文獻[1]采用了改進型的BP神經網絡PID方法控制電動舵機，實現了相比于傳統PID和BP神經網絡PID控制方法響應時間更短、超調更小、魯棒性更強的控制目標；文獻[2]采用小波神經網絡PID控制電動舵機的偏轉，增強了系統的動態響應性能；文獻[3-4]利用模糊PID控制技術改變系統阻尼比來達到提高伺服系統跟蹤性能的目的；文獻[5]采用改進型變阻尼控制算法達到了加快系統響應速度和減小超調量的目的。

模糊控制需要根據實際經驗來制定模糊控制規則，BP神經網絡和小波神經網絡控制需要恰當地設定各層權值系數，實現起來均有一定難度。遺傳算法思想簡單，易于實現，為了更好地改善隨動控制系統的動態性能，本文嘗試采用遺傳算法來實現隨動系統的自適應變阻尼控制。

1舵機模型的建立

1.1模型選擇

文獻[6-9]對電動舵機進行了數學模型的建立，控制指標要求不同，電機選型不同，所建立系統數學模型的傳遞函數就不同。本文選用文獻[9]中所建立的電動舵機模型進行研究，對基于改進遺傳算法的變阻尼隨動控制系統進行驗證。系統的開環傳遞函數和閉環傳遞函數分別為

(1)

(2)

一般來講，閉環主導極點是指在系統的所有閉環極點中不靠近任何閉環零點且距離虛軸最近的極點，而其他極點均遠離虛軸[10]。閉環主導極點對系統響應起主要作用，而其他極點的作用可忽略不計。本系統中閉環主導極點為p1，2=-66.2±j122.6，p3=-1 867.6。p1，2距離虛軸最近且周圍無閉環零點，p3遠離虛軸，因此，本系統的時間響應可以用這一對閉環主導極點p1，2所確定的二階系統的時間響應來近似，后文對此進行了驗證。

1.2傳遞函數簡化

傳遞函數簡化方法如下，由于只關注閉環主導極點，則特征方程為

(s-p1)(s-p2)=0

(3)

假設p1=a+jb，則p2=a-jb。代入式(3)，可得

s2-2ax+a2+b2=0

(4)

假設特征方程為

(5)

式中：ξ為系統阻尼比；ωn為無阻尼自然頻率。比較式(4)與式(5)可得

(6)

易求得：ωn=139.3 rad/s，ξ=0.475。

簡化后傳遞函數為

(7)

即

(8)

系統輸入單位階躍信號和隨機信號時的響應如圖1所示，簡化前與簡化后系統的響應曲線幾乎完全吻合，系統傳遞函數簡化成功。

圖1　不同輸入時隨動系統響應結果

2模型參數分析

2.1參量ωn及ξ對舵控系統性能的影響

若保持ξ不變而增大ωn，則系統超調量不變，而延遲時間、峰值時間、上升時間和調整時間均會變小，有利于提高系統的靈敏性，即系統的快速性好，如圖2所示。故增大系統的無阻尼自然頻率對提高系統的性能是有利的。

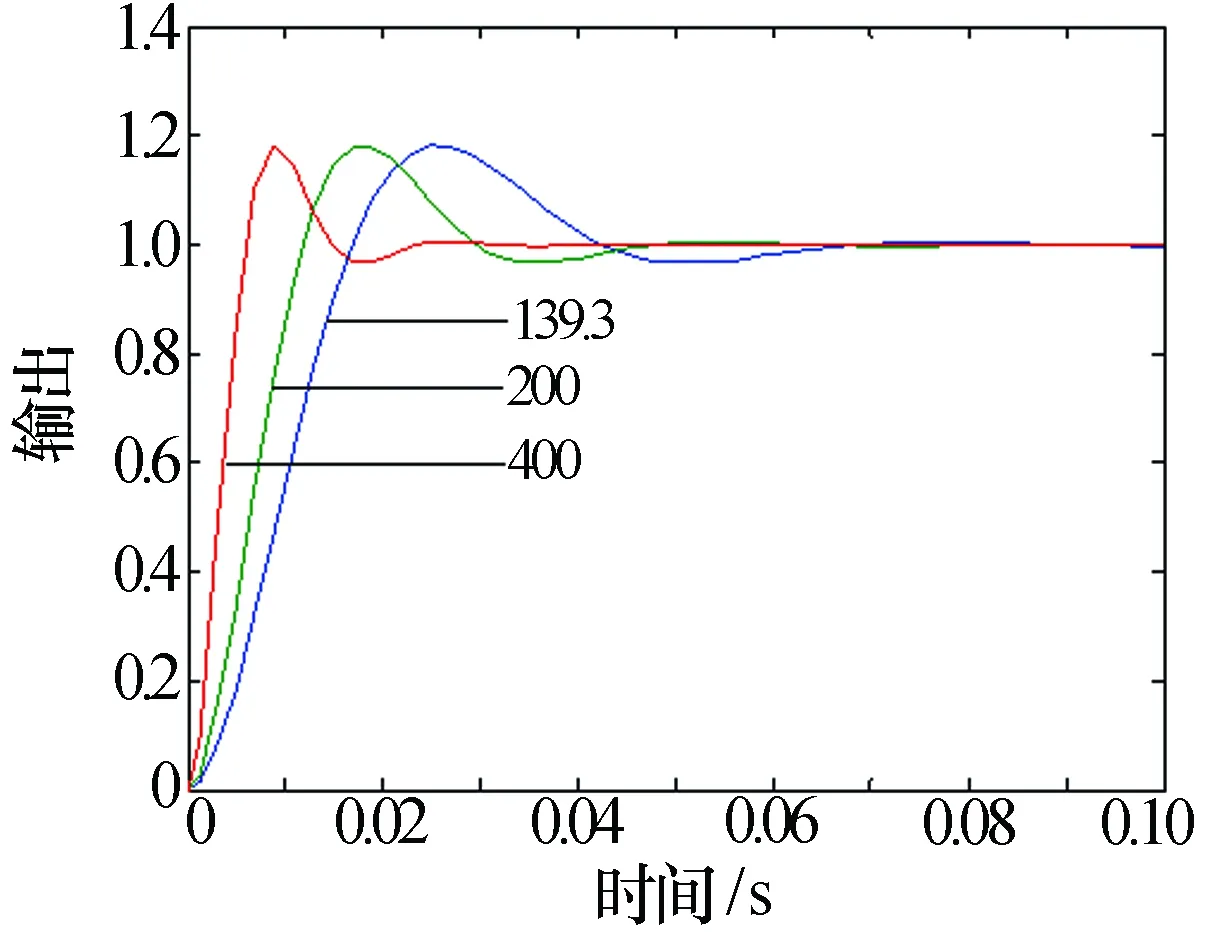
圖2　不同ωn時單位階躍響應曲線

若保持ωn不變而改變ξ。若減小ξ，雖然延遲時間、峰值時間和上升時間均會變短，靈敏性增強，但超調量會增大，相對穩定性變差。ξ越小，系統振蕩越厲害，調整時間越長。當ξ=0時，系統以無阻尼自然頻率ωn=139.3 rad/s(即f=ωn/2π=22.2 Hz)作等幅振蕩，如圖3a)所示。若增大ξ，雖然超調量減小，但延遲時間、峰值時間、上升時間和調整時間均會增大，靈敏性減弱，ξ越大，系統越不靈敏，當ξ>1時，系統蛻變為一階系統，如圖3b)所示。因此，適當選擇ξ大小，可以使二階系統具有較好的瞬態響應性能。ξ<0.4，系統嚴重超調；ξ>0.8，系統反應遲鈍。通常ξ取0.4～0.8。

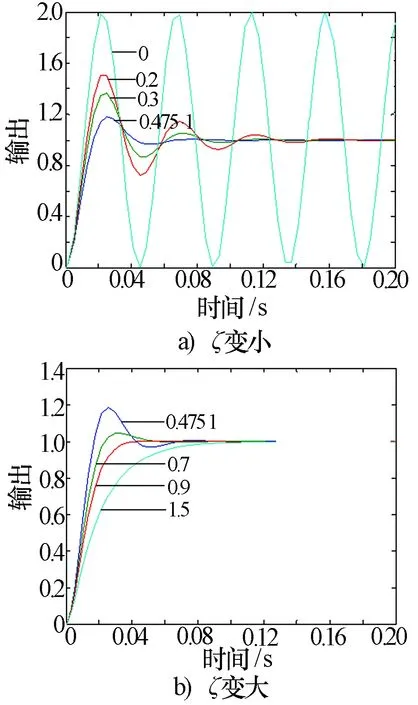
圖3　不同ξ時單位階躍響應曲線

2.2舵控系統阻尼比ξ的確定

對于本文所研究舵控系統而言，應綜合考慮系統的相對穩定性和響應快速性，通常先根據設計指標所要求超調量確定系統阻尼比ξ，再調整ωn來增強系統靈敏性。假定指標要求超調量小于10%，則當ξ=0.6時，Mp=9.5%，符合指標要求。

3自適應遺傳變阻尼控制方法

為了更直觀地觀察阻尼比，將阻尼比單獨提取出來，可以將簡化式(7)還原成圖4的形式。要改變阻尼比，即改變圖4中阻尼比ξ的值。對于電動舵機伺服系統而言，在ωn一定的情況下，系統的動態性能主要受阻尼比ξ的影響，增大阻尼比，超調量減少，但上升時間變長，系統靈敏性降低；減小阻尼比，上升時間變短，系統靈敏性增強，但超調量增大。因此，隨動系統的靈敏性與穩定性是相互對立的。為了解決這一問題，本文提出了基于遺傳算法的自適應變阻尼控制器，來實現阻尼比的實時改變，以提高系統的穩定性和靈敏性。

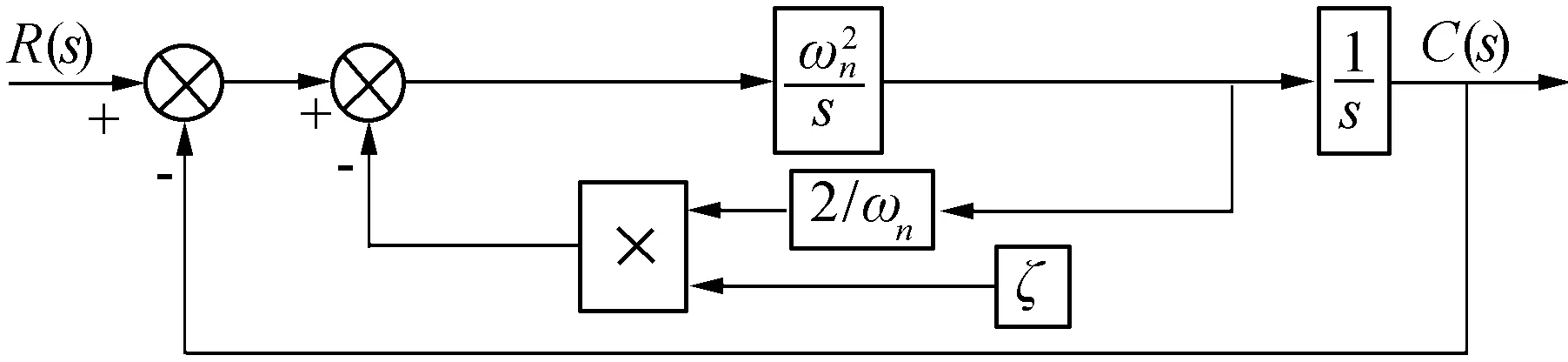
圖4　傳遞函數G1的框圖

3.1變阻尼控制器

圖5為所采用的變阻尼控制器原理框圖，e為系統誤差，ec為系統誤差絕對值的變化率，實現了根據系統誤差和誤差變化率實時改變阻尼系數。由圖5的變阻尼控制器原理框圖，得阻尼系數計算公式為

ξ0=ξ(1-Kp|e|-Kdec)

(9)

可見，阻尼系數與系統誤差e和誤差變化率ec有關，當系統誤差e的絕對值增大時，ec為正值，系統阻尼比減小，系統靈敏性增強，使得上升時間變短；當系統誤差e的絕對值減小時，ec為負值，系統阻尼比增大，系統穩定性增強，避免產生過大超調。

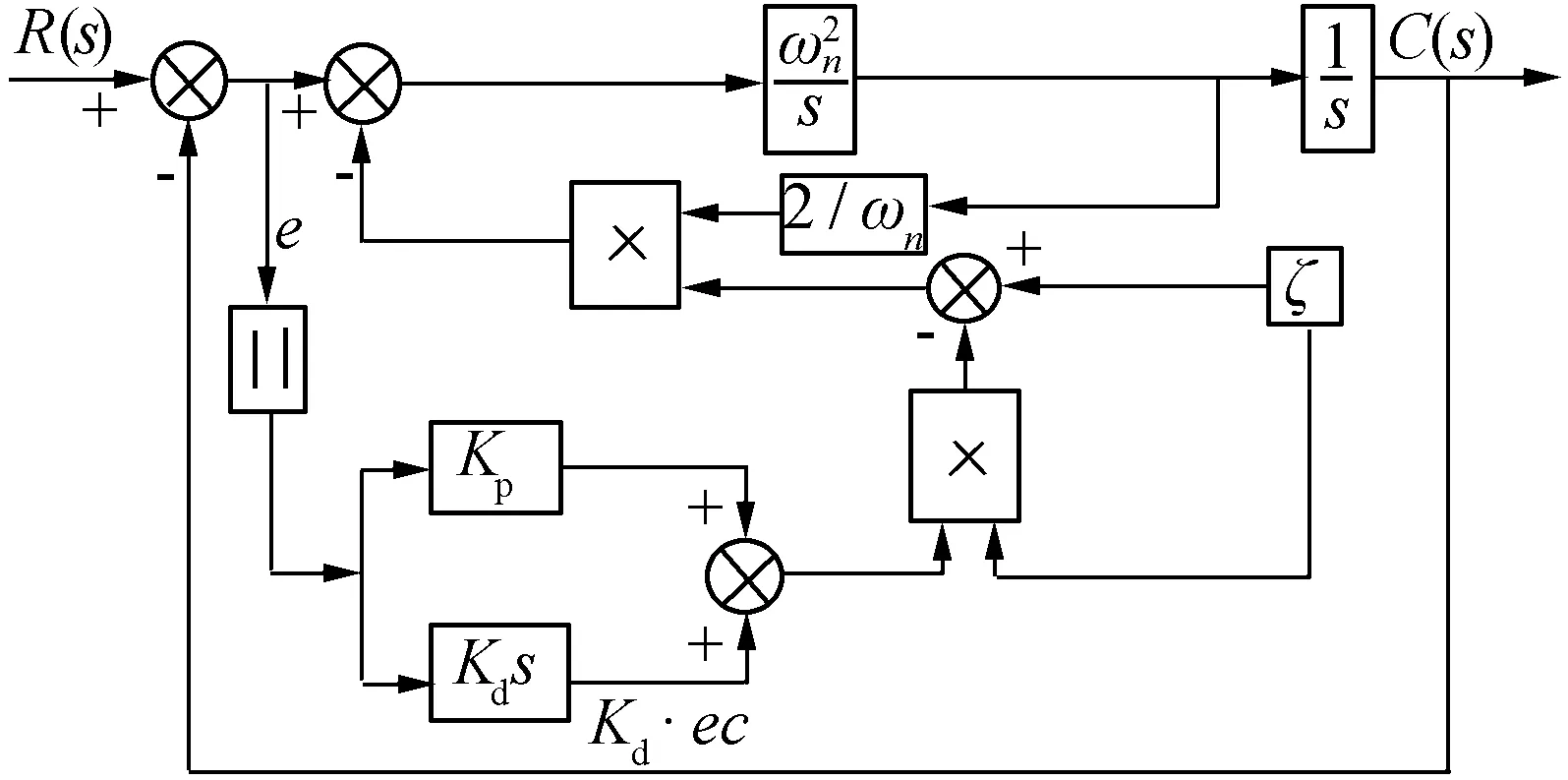
圖5　變阻尼控制器結構圖

圖6為采用恒定阻尼與變阻尼控制時系統單位階躍響應對比情況。可以看出，采用變阻尼控制時，系統上升時間與超調量均明顯小于阻尼恒定時的情況。圖7為在系數Kp與Kd固定的情況下，系統變阻尼控制時誤差和阻尼系數隨時間變化情況。可以看出，系統誤差較大時，阻尼比很小，接近于零；隨著誤差減小，阻尼快速增大；當誤差再次出現時，阻尼又往小處變化，隨著誤差再次變小，阻尼再次增大；最終，阻尼系數穩定在一個較高水平上，此時系統穩定。

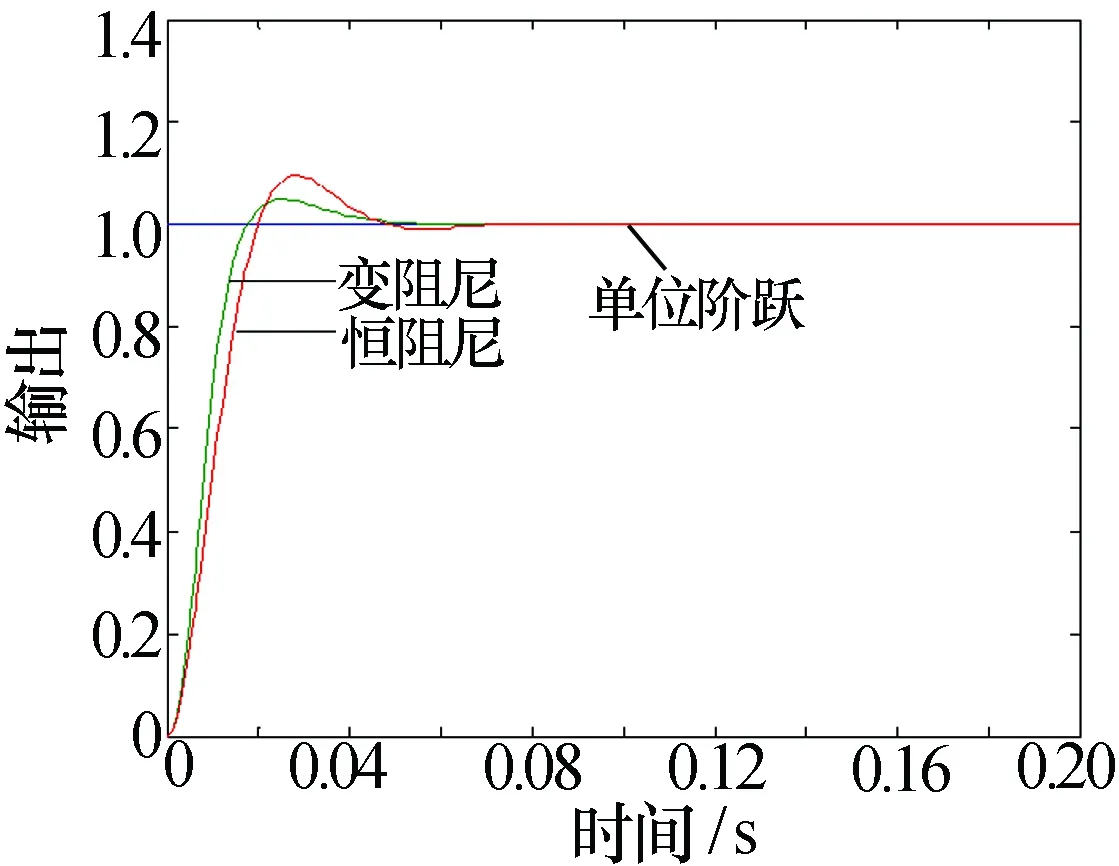
圖6　恒阻尼與變阻尼單位階躍響應對比圖

圖7　變阻尼控制誤差與阻尼比變化圖

3.2自適應遺傳變阻尼控制器

上文采用變阻尼控制時系數Kp，Kd是確定的，Kp=1.7，Kd=0.005。這是在不斷試驗中得到的數據。通過圖6可以看出，相比于恒定阻尼時，變阻尼控制時動態性能有了很大提升，但仍然存在一定的超調。為此，設計了自適應遺傳變阻尼控制器，即在每個時間點分別自適應的對參數Kp，Kd進行整定，得到了更好的效果，圖8為自適應遺傳變阻尼控制器原理圖。

圖8　自適應遺傳變阻尼控制器結構圖

在某個采樣時間，選取足夠多的個體，選擇適應度大的個體對應的參數作為該時間點下的控制參數。采用誤差的絕對值和誤差變化率的加權作為目標函數。

J=a|e|+b·ec

如果產生超調，將超調量作為最優指標，此時，最優指標為

J=a|e|+b·ec+100|e|

這樣很容易將目標函數值大的個體淘汰掉，目標函數值小(即適應度大)的個體留存。取a=0.95，b=0.05。交叉概率取0.9，變異概率為0.1。參數Kp的取值范圍為[1.6,1.8]，參數Kd的取值范圍為[0.004,0.006]。遺傳算法流程圖如圖9所示。

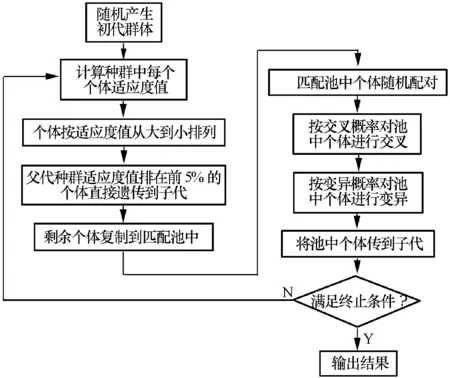
圖9　遺傳算法程序流程圖

4仿真結果

4.1仿真框圖

變阻尼控制仿真框圖如圖10所示。在此需要說明的是：(1)仿真時，誤差e取絕對值后乘了一個系數K1，如果系統輸入是單位階躍函數，此系數取1；否則，此系數取輸入函數幅值的倒數。(2)仿真圖中的限幅環節是為了保證阻尼比處于0～1之間，使系統始終工作在欠阻尼狀態，保持穩定。(3)Kp，Kd的值由遺傳算法實時決定。(4)S函數yichuan.m的程序按照圖9遺傳算法程序流程圖編寫。

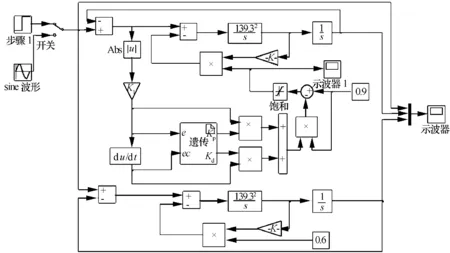
圖10　傳遞函數G1(s)自適應遺傳變阻尼控制仿真框圖

4.2仿真結果

圖11a)為阻尼比分別為0.6和自適應變阻尼時的單位階躍響應，從圖中可以看出，采用自適應遺傳變阻尼控制算法，超調量減小，上升時間、峰值時間和調整時間明顯減短。圖11b)為正弦輸入時的響應曲線。從圖11可以看出，采用變阻尼控制后，系統動態性能明顯改善。

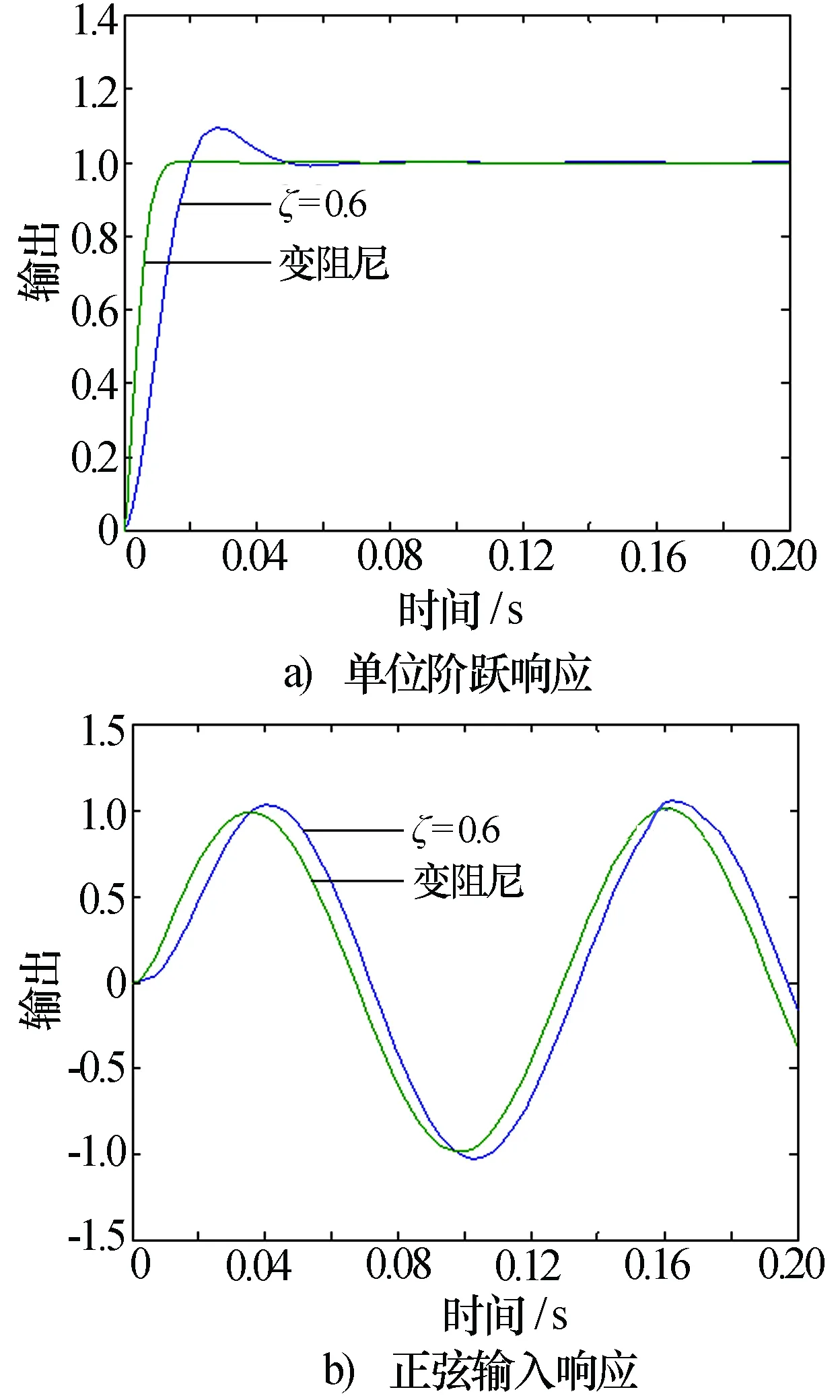
圖11　不同輸入時變阻尼控制與ξ=0.6響應結果

5結束語

本文在分析舵機傳遞函數的基礎上，簡化了其傳遞函數，分析了無阻尼自然頻率和阻尼比對系統動態性能的影響，結合常規PID控制結構簡單、易于實現和遺傳算法自適應能力強的優點，設計了基于自適應變阻尼控制算法的變阻尼控制器。仿真結果對比表明：自適應變阻尼控制方法可以優化隨動系統的動態響應性能，系統響應速度快，無超調。

參 考 文 獻

[1]張元，周長省，鄭健. 改進型BP網絡PID在電動舵機控制中的應用[J]. 彈箭與制導學報，2011, 31(6)：34-36.

ZHANG Yuan，ZHOU Changxing，ZHENG Jian. The application of the improved PID control based BP neural network of brushless DC motor[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2011, 31(6)：34-36.

[2]顧洲，朱建忠. 基于WNN-PID的直流電機位置跟蹤控制[J]. 電光與控制，2007, 14(3)：118-121.

GU Zhou，ZHU Jianzhong. A WNN-PID based controller for DC motor's position tracking[J]. Electronics Optics & Control，2007, 14(3)：118-121.

[3]王紅茹，王建中. 輕武器伺服跟蹤的模糊PID變阻尼控制[J].北京理工大學學報，2009,29(10)：861-864.

WANG Hongru，WANG Jianzhong. Variable damping ratio control by fuzzy PID for servo tracking system mounted with a small arm[J]. Transactions of Beijing Institute of Technology，2009，29(10)：861-864.

[4]鐘斌，程文明，唐連生, 等. 隨動系統的模糊自適應整定PID變阻尼控制[J]. 系統仿真學報，2006，18(11)：3200-3203.

ZHONG Bin，CHENG Wenming，TANG Liansheng，et al. Variable damping ratio control of servo system by fuzzy adaptive adjust PID[J]. Journal of System Simulation，2006，18，(11)：3200-3203.

[5]陳桂，萬其. 改進型變阻尼控制算法在隨動系統中的應用[J]. 現代雷達，2014，36(10)：70-73.

CHEN Gui，WAN Qi. Application of improved variable damping ratio control algorithm in servo systems[J]. Modern Radar，2014,36(10)：70-73.

[6]侯曉松. 基于DSP的彈上舵機控制系統的設計[D]. 西安: 西安電子科技大學, 2008.HOU Xiaosong. Design of the steering engine control system for missiles based on DSP[D]. Xi′an: Xidian University, 2008.

[7]劉煜，張科，李言俊. 一種位置隨動控制系統的建模與仿真研究[J]. 彈箭與制導學報，2005，25(2)：4-6.

LIU Yu，ZHANG Ke，LI Yanjun. Modeling and simulation research of control system of a random position[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2005, 25(2)：4-6.

[8]張明月. 滾珠絲杠式電動舵機非線性分析及控制策略研究[D]. 北京: 中國科學院大學, 2014.

ZHANG Mingyue. Nonlinear analysis and control of EMA with ball screw drive[D]. Beijing: University of Chinese Academy of Sciences, 2014.

[9]秦文甫. 基于DSP的數字化舵機系統設計與實現[D]. 北京：清華大學，2004.

QIN Wenfu. The design & implementation of actuator-based DSP[D]. Beijing：Tsinghua University，2004.

[10]董霞，陳康寧，李天石. 機械控制理論基礎[M]. 西安：西安交通大學出版社，2005.

DONG Xia，CHEN Kangning，LI Tianshi. Mechanical control theory[M]. Xi′an：Xi′an Jiaotong University Press，2005.

張文文男，1989年生，碩士研究生。研究方向為動態測試與智能儀器。

王建偉男，1979年生，高級工程師。研究方向為自動化測試技術。

侯文男，1967年生，博士，教授。研究方向為自動化測試與控制技術、動態測試與智能儀器。

Application of Variable Damping Ratio Control Algorithm in Servo System

ZHANG Wenwen1，WANG Jianwei2，HOU Wen3

(1. School of Instrument and Electronics, North University of China,Taiyuan 030051, China) (2. Nanyang Hongyu Mechatronic Machining Limited Corporation,Nanyang 474675, China) (3. School of Information and Communication Engineering, North University of China,Tiayuan 030051, China)

Abstract：In order to improve the dynamic performance of the electric servo system, an variable damping ratio control method which is adaptive is proposed. Firstly, we analyze the transfer function and simplify it. Secondly, influence of undamped natural frequency and damping ratio on the system is analyzed. Thirdly, a new variable damping ratio controller is designed which is based on the adaptive algorithm. It has the advantages of PID control and genetic algorithm. Finally, the simulation results show that the new variable damping ratio controller can improve the dynamic performance significantly and has no overshoot with high speed response while using step signal as input signals.

Key words：servo system; variable damping ratio control; genetic algorithm

DOI：10.16592/ j.cnki.1004-7859.2016.05.015

通信作者：張文文Email：470244036@qq.com

收稿日期：2016-01-22

修訂日期：2016-03-25

中圖分類號：TN820.3

文獻標志碼：A

文章編號：1004-7859(2016)05-0064-05