錯誤的“水土壓力統一計算理論”和“考慮土對水吸附性的滲流破壞理論”
——與王洪新先生商榷《考慮土對水吸附性的滲流破壞理論與應用》一文

方玉樹（后勤工程學院，重慶　400041）

?

錯誤的“水土壓力統一計算理論”和“考慮土對水吸附性的滲流破壞理論”
——與王洪新先生商榷《考慮土對水吸附性的滲流破壞理論與應用》一文

方玉樹
（后勤工程學院，重慶400041）

摘要：王洪新在《巖石力學與工程學報》2013年5期發表的《考慮土對水吸附性的滲流破壞理論與應用》一文，著重研究考慮土對水吸附性的滲流破壞和基坑突涌穩定性計算以及作為這些計算基礎的水壓率、浮力、浮重度、滲透力等議題，也據此對他本人先前關于水土壓力統一計算的論述進行了修正。結合水壓率理論對該文發表不同看法。

關鍵詞：水壓率；浮重度；滲透力；水力坡度；擋墻側壓力；基坑突涌穩定性

王洪新先生在《巖石力學與工程學報》2013年5期發表的《考慮土對水吸附性的滲流破壞理論與應用》一文，著重研究考慮土對水吸附性的滲流破壞和基坑突涌穩定性計算以及作為這些計算基礎的水壓率、浮力、浮重度、滲透力等議題（他將這些論述稱為“考慮土對水吸附性的滲流破壞理論”），也據此對他本人先前關于水土壓力統一計算的論述（他將其稱為“水土壓力統一計算理論”）【1，2】進行了修正。筆者在2007年發表的水壓率理論【3】對這些議題均已有研究，現結合水壓率理論對該文發表不同看法。

1　水壓率的理解、計算和用詞

1.1水壓率的理解

水壓率理論【3】在孔隙水壓力是單位面積土截面上的水壓力、孔隙水壓力（及總應力和有效應力）所涉及的截面是在顆粒（或膠團）之間通過的宏觀上是平面的曲面、結合水不傳遞水壓力這三個基礎上，提出下列孔隙水壓力表達式（稱水壓原理）并將有效應力原理建立在水壓原理這個基礎上：

式中u-孔隙水壓力，γw-水重度，h-壓力水頭，ξ-水壓率，為土截面上的自由水面積率，即孔隙水壓力與水體中的水壓應力（即水體水壓強）的比率。

根據王先生給出的擋墻側壓力計算公式【即本文（30）和（31）式】中的水壓力項ξsγwh可知，王先生事實上接受并引用了水壓率理論給出的（1）式，只是將水壓率改稱為產生浮力截面上自由水所占面積與截面總面積之比或土中水的壓力系數，并將其符號改為ξs。

但王先生認為水壓率理論中的水壓率屬于體積比性質，這是對水壓率理論的誤解。水壓率理論將水壓率明確定義為土截面上的自由水面積率，即孔隙水壓力與水體中的水壓應力（即水體水壓強）的比率。因此，水壓率屬于面積比性質而不是體積比性質。其實，因水壓是面力，“水壓率”一詞本身就說明它屬于面積比性質。筆者只是曾提出用自由水體積與孔隙體積之比這個體積比（也即用給水度與孔隙度之比）來估計土體內部的水壓率而已。鑒于按這種方法估計的水壓率在理論和實作上都偏小，筆者現已放棄這種方法而提出采用特殊形狀土體抗浮試驗和水荷載作用下的單向壓縮試驗測定土體內水壓率的方法【4】。

1.2水壓率的計算

王先生新給出了ξs與初始水力坡度ib的如下關系式（王先生稱其為理論關系式）：

此外，王先生還認為“梅國雄等所做的浮力實驗（注：指土上物體浮力試驗）得到的土中浮力與阿基米德定律計算的浮力之比可以看作ξs，但浮力試驗由于浮體存在側摩阻力容易出現較大誤差”。按王先生的意思，如果克服了浮體的側摩阻力（將物體無埋深地置于土體表面就能做到這一點），ξs就能根據土上物體浮力試驗確定，也就是說，土體與物體接觸面的ξs就是土體內部的ξs。

王先生的這些做法和認識都是不正確的。

1.水頭差由滲流中的阻力引起，沒有滲流就沒有水頭差也就沒有水力坡度，故初始水力坡度是不存在的；另外，達西定律不含初始水力坡度，故接受初始水力坡度這個概念還會造成達西定律和相應滲透系數定義與數據對細粒土的失效【3，5，6】，因此，（2）式是錯誤的。

2.土體內部水壓率和土體與其它物體接觸面水壓率是不同的。當接觸面非膠結面時，土體與其它物體接觸面水壓率一般大于土體內部水壓率，土的稠度越大，兩者差別越大。物體置于堅硬致密土體上時，雖然土體內部的水壓率幾乎為0，但土體與物體接觸面因是不連續面（間斷面），其水壓率則遠遠大于0。對無膠結和結晶聯結的有粘性土而言，土體內外水壓率的差異類似于土體內外粘性的差異，但數值大小關系相反。當接觸面為膠結面（如在土體表面現澆的混凝土構件與土體的接觸面）時，其水壓率可取與土體內部水壓率【3，5，6】，因此，土上物體浮力試驗得到的水壓率是土體與物體接觸面的水壓率而不是土體內部的水壓率。

1.3水壓率的用詞

水壓率理論中的“水壓率”過去就被王先生改稱為“孔隙水壓力折減系數”、“能夠產生孔隙水壓力的比率”、“能夠產生孔隙水壓力的比率系數”、“土水共同作用系數”、“土水共同作用壓力系數”、“浮力折減系數”【1，2】，如今又被其改稱為“產生浮力截面上自由水所占面積與截面總面積之比”或“土中水的壓力系數”。如此頻繁變換水壓率稱謂的做法是極不嚴肅的。當有研究者在文章中首次使用某個術語表達某個概念時，后來的研究者應繼續使用這個術語，除非使用一個新的術語更加恰當。當認為使用一個新的術語更加恰當時，也應說明情況。王先生不僅未說明情況，就連這些稱謂就是水壓率、是水壓率的替換稱謂這一點也未告知，這種刻意回避水壓率稱謂的做法是錯誤的。

考慮到水壓率這個參量反映的是單位土截面上的水壓力（即孔隙水壓力）占單位水截面上的水壓力（即水體水壓強）的比例（即兩種水壓之比率），且這個參量是一個新的水理性質指標【3】，將這個參量稱為水壓率是恰當的。

替換水壓率的上述8個稱謂并不比“水壓率”更恰當，這是因為：1.“能夠產生孔隙水壓力的比率系數”語法有誤、語義不明；2.“土中水的壓力系數”、“土水共同作用系數”與“土水共同作用壓力系數”中，“系數”一詞本身不一定是“比率”（如滲透系數、摩擦系數）；3.“土中水的壓力系數”一詞也可以理解為水壓率與水重度的乘積；4.“土水共同作用系數”與“土水共同作用壓力系數”中作用和壓力類型不明（未表明是水壓力）；5.“土水共同作用壓力系數”將“作用”與“壓力”組合在一起不恰當（壓力本身就是作用）；6.“浮力折減系數”和“產生浮力截面上自由水所占面積與截面總面積之比”混淆了浮力與孔隙水壓力兩個概念；7.“孔隙水壓力折減系數”未反映孔隙水壓力與水體水壓強相等的情形。因而這8個用詞都沒有清楚地反映孔隙水壓力與水體水壓強這兩種水壓之比率。此外，這8個稱謂均相對不夠簡潔，均不適用于一個新的水理性質指標的命名。因此，用王先生的這8個詞替換水壓率是多余的，也不利于理解。

2　浮力的計算

對頂面不低于水位面的結構物和以地面為頂面且地面不低于水位面的土體，水壓率理論給出的結構物和土體所受浮力F公式為【3】：

式中，V為結構物水下部分體積。

王先生給出的土中結構物所受浮力公式除了將水壓率ξ換為土中水的壓力系數ξs外，其余與上相同。由于土中水的壓力系數ξs就是水壓率理論中的水壓率ξ，故王先生的土中結構物所受浮力公式事實上引自水壓率理論，但王先生沒有給出浮力公式適用范圍，這意味著在王先生看來水壓率理論給出的（3）式對所有情形都適用。此外，王先生給出的浮力公式雖是針對結構物的，但王先生在計算膠團（顆粒與結合水的組合體）所受浮力時也用該公式，這意味著在王先生看來水壓率理論給出的（3）式也適用于土體和土體中的微單元。

王先生的這些做法和認識是錯誤的：

1.（3）式對與地下水連通且水位與之相同的地表水位面下方的結構物和土體不適用。對這種情形，根據結構物或土體底面與頂面水壓差可得如下浮力計算公式【3】：

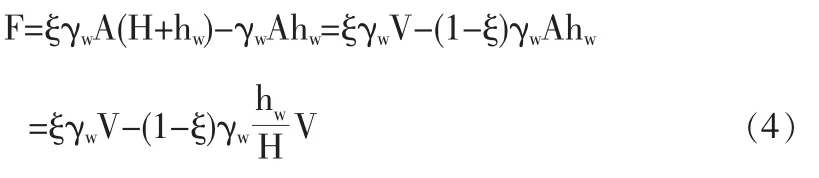
式中A為結構物或土體底面積，hw為結構物或土體頂面處壓力水頭（即水深），H為結構物或土體高度，ξ為結構物底面（即結構物與土體接觸面）或土體底面水壓率。由此可知，當結構物底面總水壓因水壓率很小而小于頂面總水壓或土體底面總水壓因水壓率很小而小于地面總水壓時，浮力方向朝下。

2.（3）式作為土體中微單元浮力計算方法對多層土體不適用。

由（4）式可得單位體積浮力計算公式：

從上式可知，當水位面高于地表且土的水壓率不等于1時，土體所受單位體積浮力計算范圍向上需到達地面，向下需到達土體底面，計算所用水壓率是土體底面的水壓率。

將（3）式用于土體所受浮力計算時，因式中水壓率是土體底面水壓率，故由（3）式計算該土體內部微單元所受浮力時水壓率也應取該土體底面水壓率而不是取該土體內部微單元所在截面水壓率。

對多層土體，各層土水壓率不同，故土體底面水壓率不同于該土體內部微單元所在截面水壓率。王先生在計算土體中膠團所受浮力時不要求水壓率取土體底面水壓率，顯然這種做法對多層土體不適用。

3.如本文1.1節所指出的那樣，土體與結構物接觸面的水壓率與土體內部水壓率是不同的。

3　浮重度的計算

3.1王先生浮重度計算方法的分析

王先生給出的浮重度γ'計算式為：

式中，γsat為飽和重度；ξ0為土水共同作用系數（注：原文符號為ξ，為與水壓率理論中的水壓率符號ξ區分開來，改用ξ0），其定義式為：

式中，ξv為自由水所占體積與孔隙總體積之比，e為孔隙比。

ξ0由（7）式定義的（6）式是錯誤的，這是因為用浮重度計算土的有效自重應力應與用有效應力原理計算土的有效自重應力等效。詳細說明如下：

根據（1）式和有效應力原理

由多個水平土層組成的土體中某點的豎向有效自重應力σ'cz應按下式計算：

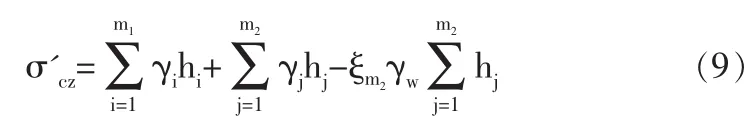
式中m1、m2分別為計算點以上土層中水位面以上和以下土層數，γi、γj分別為水位面以上第i層土和水位面以下第j層土的重度，hi、hj分別為水位面以上第i層土和水位面以下第j層土的厚度，ξm2為第m2層土的水壓率（分層界面處取較大值）。

上式可改寫為

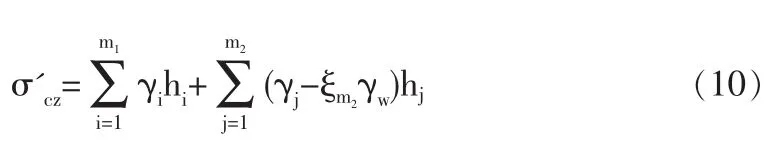
據此，計算點以上水位面以下任意一層土的浮重度為【1】

從（9）式至（11）式可得以下認識：

1.浮重度算法（指用浮重度計算土的有效自重應力的方法）與有效應力原理算法（指用有效應力原理計算土的有效自重應力的方法）中涉及的水壓率相同，也就是說，王先生中的土水共同作用系數ξ0和土中水的壓力系數ξs是同一個參數，都是水壓率理論中的水壓率。其實，（6）式與（3）式也是矛盾的。在（6）式中ξ0γw是單位體積土所受浮力，按照（3）式，（6）式中的ξ0就是ξs。

2.某層土的浮重度計算中所涉及的水壓率不是該層土的水壓率而是有效自重應力計算點所在土層的水壓率，（6）式中土水共同作用系數ξ0替換為水壓率后，（6）式對多層土仍不適用。

上述情況表明，（6）式中土水共同作用系數ξo替換為水壓率后，（6）式是水壓率理論已經給出的（11）式的特例。

3.2浮重度計算方法錯誤帶來的問題

王先生浮重度計算方法的上述錯誤必然造成用浮重度計算有效自重應力、含有效自重應力的有效應力、擋墻土壓力、滲流破壞穩定性和基坑突涌穩定性的混亂和錯誤。

以基坑突涌為例，王先生根據錯誤的（6）式得到如下錯誤的臨界方程：

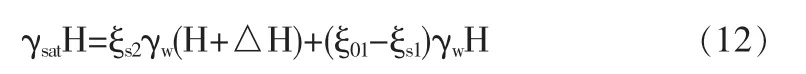
式中，ξs1，ξs2分別為承壓含水層及其頂板土中水的壓力系數，ξ01為承壓含水層頂板土水共同作用系數，γsat為承壓含水層頂板飽和重度，H為基坑底到承壓含水層頂面的距離。王先生據此得出“上覆土層有一定透水性時，上覆土層厚度要求比傳統算法計算的大，此時傳統算法是偏于不安全的”這一錯誤結論。

事實上，當上覆土層有一定透水性時，在基坑下挖的過程中，承壓水頭隨著水的滲出而降低，臨界厚度隨之減小。基坑下挖到原臨界厚度時，因臨界厚度減小，基坑突涌還未到臨界狀態。這就是說，當上覆土層有一定透水性時，上覆土層厚度要求比傳統算法計算的小，此時傳統算法是偏于安全的。當承壓含水層水壓率不等于1時更是如此。

根據（1）式和有效應力原理可寫出下列基坑突涌臨界方程：

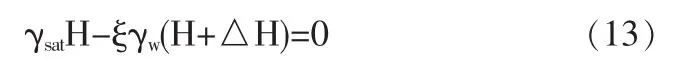
由此筆者早在2007年就得到下列基坑突涌臨界厚度計算式【1】：

因承壓系統屬于多層土體，承壓含水層與隔水頂板、底板的水壓率差別很大，而飽和重度差別不大，故承壓含水層頂面處土體重與總孔壓差別最小。因此，基坑突涌臨界方程應建立在此處，若發生基坑突涌，此處就是基坑突涌發生的源頭。當上覆土層為不透水的黏土層時，王先生“承壓水層含有一定細粒成分時，上覆土層厚度要求比傳統算法小”的結論是（14）式的必然結果，并不需要通過（12）式得到。

3.3王先生浮重度計算公式推導過程的分析

王先生之所以得出ξ0由（7）式定義的（6）式，是因為推導過程存在錯誤。王先生通過膠團重與膠團所受浮力之差計算土的浮重，不計自由水的浮重（即將孔隙中自由水的浮重取0），同時膠團所受浮力按（3）式計算。這種推導過程存在三個問題：

1.根據本文第2部分分析結果，（3）式對與地下水連通且水位與之相同的地表水位面下方的結構物和土體不適用，故膠團所受浮力按（3）式計算的做法對與地下水連通且水位與之相同的地表水位面下方的結構物和土體不適用。

2.根據本文第2部分分析結果，計算膠團所受浮力時所用ξs應是計算浮重之土體底面的ξs而不是膠團所在截面的ξs，故采用膠團所在位置ξs計算膠團所受浮力的做法不適用于多層土。

3.當ξs不等于1時，用膠團浮重代表土體浮重是錯誤的。土體浮重是膠團浮重與膠團間自由水浮重之和。自由水體積為ξve△Vs，自由水重為ξvγwe△Vs，自由水所受浮力為ξsξvγwe△Vs（△Vs為土單元顆粒體積），故自由水浮重為（1-ξs）ξvγwe△Vs。把自由水浮重計入土的浮重后，所得浮重度中土水共同作用系數ξ0便與土中水的壓力系數ξs相等。

順便指出，王先生在浮重度推導中用到的ξsγw［1+（1-ξv）e］△Vs是膠團所受浮力，王先生將其稱作“土顆粒（體積為△Vs）受到的浮力”是錯誤的。

從這里可以看出，通過分析土中各個組分的浮重來推導土的浮重度不僅繁瑣而且容易出現差錯，直接用（1）式和有效應力原理來推導則很簡單；對多層土，因浮重度計算公式中的水壓率隨有效自重應力計算點所在土層的不同而不同，用浮重度計算有效自重應力不僅不能簡化計算過程而且容易出現差錯，直接用（1）式和有效應力原理來計算則比較簡單。這正是水壓率理論【3】已經得出的結論。

4　滲流破壞臨界方程

土體浮動臨界狀態滿足下列方程：

式中，σ為土體底面總應力，u為土體底面孔隙水壓力。

當滲流方向垂直向上、水位高于地面時，對以地面為頂面的直立土柱，土柱底面總應力為：

式中h為土柱底面壓力水頭，ξn為土柱底面水壓率（在分層界面取較大值）。因此，（15）式可寫成

上式可寫成：

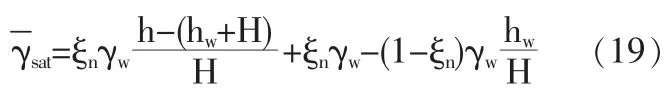
因h-（hw+H）為土柱底面與頂面水頭差△z=z2-z1【z1，z2為土柱頂面（即地面）、底面水頭高度】，故上式可寫成：

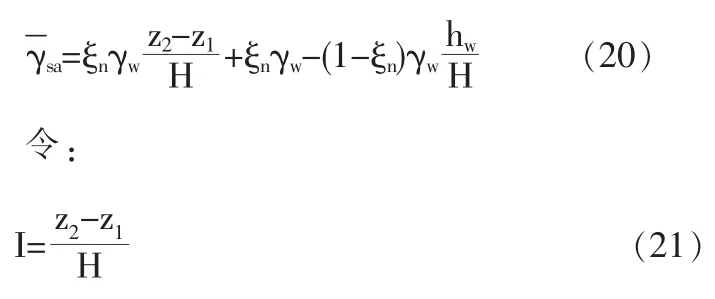
式中I為水力坡度。由此，（20）式可寫成

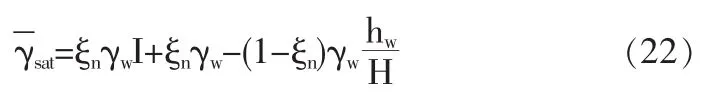
上式右邊隨土體底面水壓率ξn的減小而減小。由此式可得下列臨界水力坡度計算式：

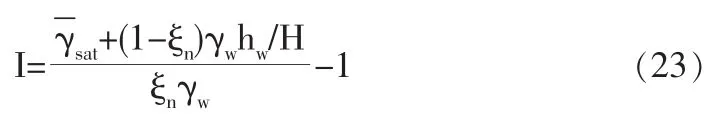
筆者曾給出下列臨界水力坡度計算式【3】：

顯然上式只適用于無地表水的情形。當ξn=1時，（23）式成為

因土的飽和重度相對變化范圍小于水壓率變化范圍，故由（23）式知，多層土柱的底面應取在水壓率最大土層的頂面。

根據（23）式可以分析為何有時水力坡度遠大于1時沒有發生流土，也可以分析為何有時水力坡度遠小于1時發生了潛蝕。對潛蝕而言，式中飽和重度應是粗粒間由細粒和水構成的土管的飽和重度，它隨土管內細粒土密實度變化，土管內只有幾個細粒時，土管飽和重度接近于自由水重度。

王先生針對多層土中任意土層給出如下滲流破壞極限平衡方程【為避免與（20）式中角標數字混淆，用i和i+1替換原文中的1和2；為避免與壓力水頭混淆，用z替換原文中的h】：

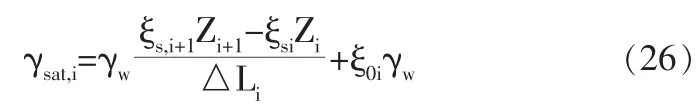
式中，ξsi，ξs，i+1為第i土層頂面、底面土中水的壓力系數，ξ0i為第i土層頂面土水共同作用系數，△Li為第i土層高度，zi，zi+1為第i土層頂面、底面水頭高度。

王先生的做法存在下列問題：

1.未將式中ξ0i取與ξsi相同的值。

2.既不要求選擇水壓率最大土層的頂面做土柱的底面，也不要求以地面為土柱的頂面，導致方程失效：在水壓率最大土層頂面做底面、地面做頂面的土柱中，因受其它層影響，某層滿足（26）式不代表土柱要發生滲流破壞，某層不滿足（26）式（等號左邊大于右邊）也不代表土柱不發生滲流破壞。因而，ξ0i取與ξsi相同的值后，（26）式仍是錯誤的。

5　滲透力和水力坡度的計算

5.1滲透力的計算

王先生針對多層土中任意土層給出如下單位體積滲透力Di表達式【為避免與（20）式中角標數字混淆，用i和i+1替換原文中的1和2；為避免與壓力水頭混淆，用z替換原文中的h】：

式中各符號意義同前。

王先生還將土對水無吸附性時式中γwZi，γwZi+1解釋為第i土層頂面和底面受到的土中水壓力。

這些做法存在下列問題：

1.式中的水頭是總水頭而不是壓力水頭，土對水無吸附性時，式中γwz1，γwz2顯然不是土單元頂面和底面受到的土中水壓力。

2.根據（5）式，（20）式中ξnγw-（1-ξn）γwhw/H為單位體積土體所受浮力，因此，（20）式中涉及水頭差項ξnγw（z2-z1）/H就是單位體積土體所受滲透力，即有

從（5）式可知，當有與地下水連通的地表水且土的水壓率不等于1時，土體所受浮力計算范圍向上需到達地面，向下需到達土體底面，計算所用水壓率是土體底面的水壓率。在滲流條件下滲透力和浮力相伴而生，針對同一個對象，故土體所受滲透力計算范圍和水壓率取值應與此相同。（27）式的計算范圍向上未到達地面，向下未到達土體底面，計算所用水壓率也不是土體底面的水壓率，因而是錯誤的。

5.2水力坡度表達式

王先生將考慮土對水吸附性后的水力坡度I表達式改為：

式中，z1，z2為土單元頂面、底面水頭高度（原文符號為h1，h2，為與相應壓力水頭清楚地區分開來，改用z1，z2）。

此式存在下列問題：

1.根據達西定律，滲透速度是滲透系數與水力坡度的乘積，其中水力坡度是沿流線的水頭損失率，與水壓率無關，采用（29）式將造成達西定律失效。

2.水力坡度涉及的水頭是總水頭，是位置水頭和壓力水頭之和，而水壓率是用于計算孔隙水壓力的，是與自由水重度、壓力水頭相伴的，總水頭與水壓率的乘積沒有物理意義。

因此，（29）式是錯誤的。

由本文第4部分可知，滲流破壞穩定性計算是力平衡問題，水力坡度概念對此可有可無。但若采用了水力坡度概念，水力坡度就應是從土柱底面到地面范圍的水力坡度（對多層土，以水壓率最大土層頂面做土柱底面）。

真正需要應用水力坡度概念的是滲流計算和與滲流有關的固結計算。在這些計算中，常常要用到土體中某點的水力坡度，此時水力坡度表達式是微分式。因此，水力坡度概念是必要的而且可以采用微分式表達。

6　擋墻側壓力的計算

王先生給出的擋墻側壓力計算公式為：

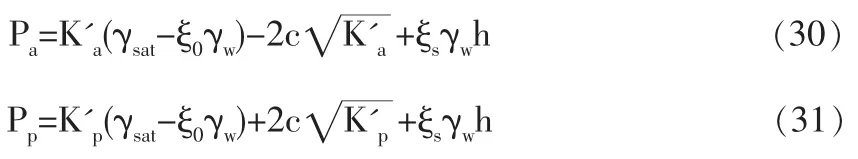
式中，h為從地面起算的計算點深度；c和φ為“統一強度指標”概念下的粘聚力和內摩擦角，按下式計算：

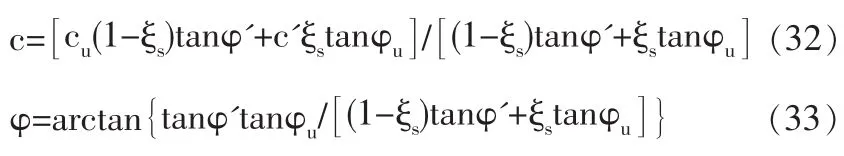
王先生的這套公式存在多方面錯誤：

1.豎向有效自重應力計算錯誤。根據（6）式知，式中豎向有效自重應力是用王先生給出的浮重度計算的，如第3部分所述，王先生的浮重度計算是錯誤的，故豎向有效自重應力計算是錯誤的。

2.“統一強度指標”概念錯誤。王先生的“統一強度指標”是將有效應力強度指標和不排水總應力強度指標組合起來使取值可在這兩類指標之間過渡的強度指標，這個概念是錯誤的。有效應力強度指標對應于剪切面上的法向有效應力，總應力強度指標對應于剪切面上的法向總應力。剪切面上的法向應力采用有效應力時應采用有效應力強度指標，剪切面上的法向應力采用總應力時應采用總應力強度指標。原則上抗剪強度均應采用有效應力和有效應力強度指標進行表達，考慮到有效應力強度指標相對不易獲取，工程實用上允許根據排水條件選用不同總應力強度指標進行表達。“統一強度指標”既不是有效應力強度指標也不是總應力強度指標，既不對應于剪切面上的法向有效應力，也不對應于剪切面上的法向總應力，是沒有意義的。擋墻水土壓力采用分算方法時，因其中土壓力強度本身及土壓力強度計算所用豎向自重應力均是有效應力，故土壓力強度計算所用抗剪強度指標應是有效應力強度指標。王先生將“統一強度指標”用于這種計算是錯誤的。根據有效應力原理，有效應力強度指標就是唯一的強度指標。

其實，飽和粘性土各類強度（及其指標）同水壓率一樣也是隨稠度的變化而變化的，這些強度（及其指標）本身會隨著稠度的增大而趨同。

飽和粘性土軸對稱固結不排水三軸試驗中孔隙水壓力這個超孔隙水壓力△u與大小主應力增量差（△σ1-△σ3）的關系式為（式中A為孔隙壓力系數）：

眾所周知，孔隙壓力系數A隨粘性土稠度的增加而降低。根據（34）式，隨著孔壓系數A減小直至0，超孔隙水壓力減小直至0，有效應力增大直至總應力，此時，有效應力強度（及其指標）與固結不排水強度（及其指標）、固結排水強度（及其指標）趨于相等。同時，當稠度很大時，土的變形模量很大，土的固結變形量很小，因而固結不排水強度（及其指標）與不固結不排水強度（及其指標）也趨于相等。當飽和土不含自由水（如堅硬致密粘土）時，因土不再滲透固結，有效應力強度（及其指標）與固結不排水強度（及其指標）、不固結不排水強度（及其指標）、固結排水強度（及其指標）相同。這正是水壓率理論【3】認為“當水壓率很小時……有效應力強度指標接近于總應力強度指標，有效土壓力系數接近于總土壓力系數”的原因。

3.上述公式的推導過程中孔隙水壓力和有效應力概念不清。

（1）根據（30）和（31）式中的水壓力項可知，王先生事實上接受了（1）式并用該式計算孔隙水壓力，但王先生又采用如下有效應力原理表達式并將式中u稱為孔隙水壓力：

這就導致u和ξu兩個孔隙水壓力。在孔隙水壓力概念不清的情況下，由（35）式表達的有效應力原理無法在文字上進行闡述。

早在王先生引用（35）式之前，李廣信先生就指出（35）式違反了有效應力原理【7】。王先生在引用李先生文章中出現的（35）式之時對此置之不理，這種做法是不正確的。

（2）眾所周知，固結不排水三軸試驗中所測孔隙水壓力是超孔隙水壓力（在單向固結試驗中超孔隙水壓力的最大值就是所施加的荷載）。其值本身就應是王先生已接受并已引用的（1）式中的u也即（35）式中的ξu。王先生卻在推導（32）和（33）式的過程中將所測孔隙水壓力視為水體水壓強γwh也即（35）式中的u（即不包含ξ），按照這種認識，若仍按（1）式計算孔隙水壓力，就會造成單向固結試驗中加載瞬間引起的超孔隙水壓力大于荷載本身，有效應力為負，土體回彈這種荒謬結果。徐日慶先生等人就曾這樣得到一維固結也可以有Mandel-Cryer效應的錯誤結論【8，9】。

令人不解的是，王先生本人已經在2012年的文章中否定了他在2011年文章中提出的（32）和（33）式并重新給出公式（自然地，由于“統一強度指標”概念本身錯誤，重新給出的“統一強度指標”公式也是錯誤和無意義的），如今王先生又在不加任何說明的情況下將其重新顛倒過來，這樣做是極不嚴肅的。

此外，（30）和（31）式等號右邊前兩項未含h，并且在給出這兩個公式時未列出墻背直立光滑、土體均質、表面水平且無附加荷載、地下水位面與土體表面平齊等條件。

上述情況表明，導出（30）-（33）式遠非王先生所說“建立起在邏輯上極為嚴謹的水土壓力統一計算理論”，恰恰相反，導出和恢復使用（30）-（33）式的過程完全無邏輯可言。

7　其它

7.1基坑突涌穩定性計算的理解

王先生將基坑突涌穩定性計算視為“上覆土層采用水土合算，承壓水層采用水土分算”。這是錯誤的。

1.水土分算和合算是當前擋墻側壓力計算的兩種算法，不涉及豎向壓力計算。在目前的擋墻側壓力計算中，由于分算和合算所用的側向土水壓力系數及強度指標不同，水土分算和合算結果是不同的。但在豎向上，無論水土分算還是水土合算，因不涉及側向土水壓力系數及強度指標，上覆土重都是相同的。由于結果相同，就無所謂水土分算和合算。

2.水土分算并不是只算其中的土壓力或只算其中的水壓力，而是水壓力和土壓力分別計算后再相加。基坑突涌穩定性計算時，對承壓含水層只需要計算承壓水在隔水頂板底面產生的壓力。這種計算顯然不是水土分算。

7.2浮力、浮重度、滲透力和水力坡度用詞

王先生將考慮結合水影響后的浮力、浮重度、滲透力和水力坡度分別稱為廣義浮力、廣義浮重度、廣義滲透力和廣義水力坡度。這是錯誤的。廣義是相對于狹義而言一個概念的適用范圍更寬的意思。考慮結合水影響后，浮力、浮重度、滲透力和水力坡度這些概念（而不是計算方法）的適用范圍沒有在既有適用范圍基礎上擴展，怎能冠以廣義一詞呢？

8　結語

1.根據王先生給出的擋墻側壓力計算公式中的水壓力項ξsγwh可知，王先生事實上接受并引用了水壓率理論提出的孔隙水壓力表達式（稱水壓原理）即（1）式；王先生給出的浮力公式即（3）式是水壓率理論給出的若干浮力公式中的一個。

2.與水壓率理論進行對比可知，“水土壓力統一計算理論”和“考慮土對水吸附性的滲流破壞理論”不同于水壓率理論之處是：

（1）回避和頻繁變換水壓率理論中的水壓率稱謂；

（2）給出水壓率與初始水力坡度的關系式即（2）式；

（3）不區分土體與物體接觸面的水壓率與土體內部的水壓率；

（4）計算物體和土單元浮力時只引用水壓率理論的兩個浮力公式中較簡單的那一個即（3）式；

（5）給出不同的浮重度計算式即（6）式；

（6）根據不同的浮重度計算式給出不同的基坑突涌臨界方程即（12）式；

（7）根據不同的浮重度計算式給出不同的滲流破壞極限平衡方程即（26）式；

（8）給出不同的單位體積滲透力表達式即（27）式和水力坡度表達式即（29）式；

（9）提出不同的粘聚力和內摩擦角計算式即（32）和（33）式（稱“統一強度指標”計算式）；

（10）引用不同的有效應力原理表達式即（35）式；

（11）根據“統一強度指標”計算式和不同的浮重度計算式給出不同的擋墻側壓力計算公式即（30）和（31）式；

（12）將考慮土對水吸附性后的浮力、浮重度、滲透力和水力坡度分別稱為廣義浮力、廣義浮重度、廣義滲透力和廣義水力坡度。

逐一分析的結果表明，這些做法都是錯誤的。其中，水壓率公式因初始水力坡度不存在而錯誤，浮重度計算式（6）式因相應有效自重應力與用有效應力原理計算所得不等效而錯誤，有效應力原理表達式（35）式和“統一強度指標”計算式（32）、（33）式因孔隙水壓力概念混亂而錯誤，水力坡度表達式（29）式因水頭概念錯誤而錯誤，基坑突涌臨界方程（12）式因浮重度計算式錯誤而錯誤，滲流破壞極限平衡方程（26）式因浮重度計算式錯誤且既不要求選擇水壓率最大土層的頂面做土柱的底面也不要求以地面為土柱的頂面而錯誤，單位體積滲透力表達式（27）式因所在滲流破壞極限平衡方程和浮力計算錯誤而錯誤，擋墻側壓力計算公式（30）和（31）式因“統一強度指標”概念和浮重度計算錯誤而錯誤。因此，“水土壓力統一計算理論”和“考慮土對水吸附性的滲流破壞理論”是完全錯誤的。

3.本人曾經詳細分析了徐日慶先生等人的“兩相非連續介質固結理論”的錯誤【9】。綜觀“水土壓力統一計算理論”、“考慮土對水吸附性的滲流破壞理論”和“兩相非連續介質固結理論”，雖然它們的錯誤不盡相同，但都有一個根本性錯誤，就是孔隙水壓力概念含混不清：有時將按水體水壓強計算的值視為孔隙水壓力，有時又將它與某個系數的乘積視為孔隙水壓力，或者同時將二者視為孔隙水壓力。這表明水壓率理論中以本文（1）式表達的水壓原理是極其重要的，研究與孔隙水壓力有關的問題須從水壓原理出發而不是從有效應力原理開始。

4.本文以及筆者此前發表的文章【4-6】表明，早在2007年就發表的水壓率理論【3】已經涵蓋了“水土壓力統一計算理論”和“考慮土對水吸附性的滲流破壞理論”以及“兩相非連續介質固結理論”所涉及的范圍，已經從理論上解決了王洪新先生和徐日慶先生等人共同或分別關注的細粒土浮力折減、水土壓力的分算和合算、考慮土對水吸附性的滲流破壞和基坑突涌穩定性計算、細粒土固結等問題以及其它與孔隙水壓力有關的問題。

參考文獻：

［1］王洪新.水土壓力分算與合算的統一算法［J］.巖石力學與工程學報，2011，30（5）：1057-1064.

［2］王洪新.水土壓力統一計算理論的證明及水土共同作用下的壓力計算［J］.巖石力學與工程學報，2012，31（2）：392-398.

［3］方玉樹.基于水壓率討論土中孔隙水壓力及有關問題［J］.巖土工程界，2007，10（5）：21-26.

［4］方玉樹.關于水壓率理論與有效應力原理的幾個問題［J］.重慶建筑，2016，15（3）：55-58.

［5］方玉樹.水壓率理論被推翻了嗎［J］.巖土工程界，2007，10（11）：21-26.

［6］方玉樹.水壓率理論釋疑［J］.巖土工程界，2008，11（4）：21-26.

［7］李廣信.再議水壓率［J］.巖土工程界，2008，11（2）：21-24.

［8］徐日慶，等.兩相非連續介質固結理論［J］.巖石力學與工程學報，2014，33（4）：817-825.

［9］方玉樹.錯誤的“兩相非連續介質固結理論”——與徐日慶先生等商榷“兩相非連續介質固結理論”一文［J］.重慶建筑，2016，15（2）：55-56.

責任編輯：孫蘇，李紅

The Fault "Unified Calculation Theory on Water-Soil Pressure" and "Seepage Failure Theory Considering Water-Soil Absorptivity"

Keywords:water pressure；submerged unit weight；seepage force；hydraulic gradient；lateral pressure of retaining wall；up-bursting stability of pit foundation

Abstract:Wang Hongxin published his paper Seepage Failure Theory and its Application Considering Water-Soil Absorptivity on Chinese Journal of Rock Mechanics and Engineering in no.5，2015，studying seepage failure considering water-soil absorptivity and the up-bursting stability calculation of pit foundation as well as the calculation bases like water pressure rate，buoyance，submerged unit weight and seepage force etc.，with his prior illustration amended.The author presents some different views on the paper based on water pressure theory.

中圖分類號：TU43

文獻標識碼：A

文章編號：1671-9107（2016）04-0053-07

doi：10.3969/j.issn.1671-9107.2016.04.053

收稿日期：2016-02-04

作者簡介：方玉樹（1958-），男，江西婺源人，碩士，教授，國家注冊土木工程師（巖土），主要從事與巖土體穩定有關的研究和勘察設計工作。