考慮相變時間效應的結冰試驗相似參數

易 賢, 周志宏, 杜雁霞, 朱國林

(中國空氣動力研究與發展中心 空氣動力學國家重點實驗室，四川 綿陽 621000)

考慮相變時間效應的結冰試驗相似參數

易 賢*, 周志宏, 杜雁霞, 朱國林

(中國空氣動力研究與發展中心 空氣動力學國家重點實驗室，四川 綿陽 621000)

結冰風洞試驗是進行飛機結冰和防除冰研究的主要手段，結冰試驗相似準則是進行結冰風洞試驗的理論基礎。針對目前的結冰試驗相似準則在明冰模擬方面的不足，本文采用液/固相變的基本理論，對飛機結冰過程的液/固相變傳熱特性進行了分析和研究。在此基礎上，提出了一個新的結冰試驗相似參數CT，該參數與基于Messinger結冰熱力學模型所得到的相似參數的主要區別是考慮到了結冰的干模式和濕模式，體現了相變的時間效應。通過將新的相似參數引入現有結冰試驗相似準則中，可有效避免試驗壓力與速度選取的隨意性。以NACA0012翼型和某超臨界翼型為對象，對新相似參數的有效性進行了數值仿真評估，結果顯示，采用本文提出的相似參數及相應的試驗參數確定方法，能夠得到與參考條件一致的水滴收集率和結冰，初步說明新相似參數的是有效的，研究結果對于提高明冰及混合冰試驗模擬的精度具有較好的參考價值。

飛機結冰；結冰風洞；結冰相似準則；結冰模型；傳熱；相變

0 引 言

飛機結冰是飛行實踐中經常遭遇的一種物理現象，也是導致飛行安全隱患的主要因素之一[1-2]，由于結冰環境的不同，結冰的類型也有所差異，典型的結冰類型包括霜冰、明冰與混合冰[3]。結冰風洞試驗是進行飛機結冰和防除冰研究的主要手段。與常規風洞試驗一樣，進行結冰風洞試驗，必須遵循一定的相似準則。由于影響結冰的因素除了空氣流場之外，還包括結冰云霧條件和飛行狀態等，因此結冰試驗相

似準則遠比常規風洞試驗所要求的相似準則復雜。由于這種復雜性，從結冰風洞建立之初，國外就開始了針對結冰試驗相似準則的研究[4-9]，國內近年來也在相關領域開展了一些研究工作[3,10]。經過研究者們多年的努力，目前的相似準則已經可以完全適用于霜冰(Rime Ice)的模擬，但在模擬明冰(Glaze Ice)和混合冰(Mixing Ice)時，參考冰形與試驗冰形之間始終存在一定程度的差異[11]，使得現有相似準則應用的普適性受到限制。

與霜冰形成完全是干模式結冰不同，明冰及混合冰的生長過程是典型的濕模式結冰[12]，其伴隨著液態水膜的形成、生長及其與冰層的相互作用。對這一復雜過程的描述，目前廣泛采用的是Messinger提出的模型[13]，該模型基于熱力學的分析方法，只從宏觀上考慮了結冰過程的能量平衡，不能刻畫結冰相變過程的傳熱學效應，尤其是忽略了相變的時間效應。而目前采用的結冰試驗相似準則對相變過程模擬的相似參數，均來源于Messinger模型，這也是在明冰和混合冰試驗中，參考冰形與試驗冰形之間始終存在一定程度的差異的原因。針對該問題，本文基于結冰過程液/固相變的基本理論[14-16]，對飛機結冰過程的液/固相變傳熱特性進行了分析和研究，提出一個考慮相變時間效應的結冰試驗相似參數CT，并采用數值手段對該相似參數的有效性進行計算評估。

1 基于Messinger模型的結冰熱力學相似參數

考慮結冰表面上某控制體積中的能量傳遞情況，Messinger將能量傳遞分成6項[13]，如圖1所示，則根據熱力學第一定律，控制體積表面的能量平衡方程可以寫成：

(1)

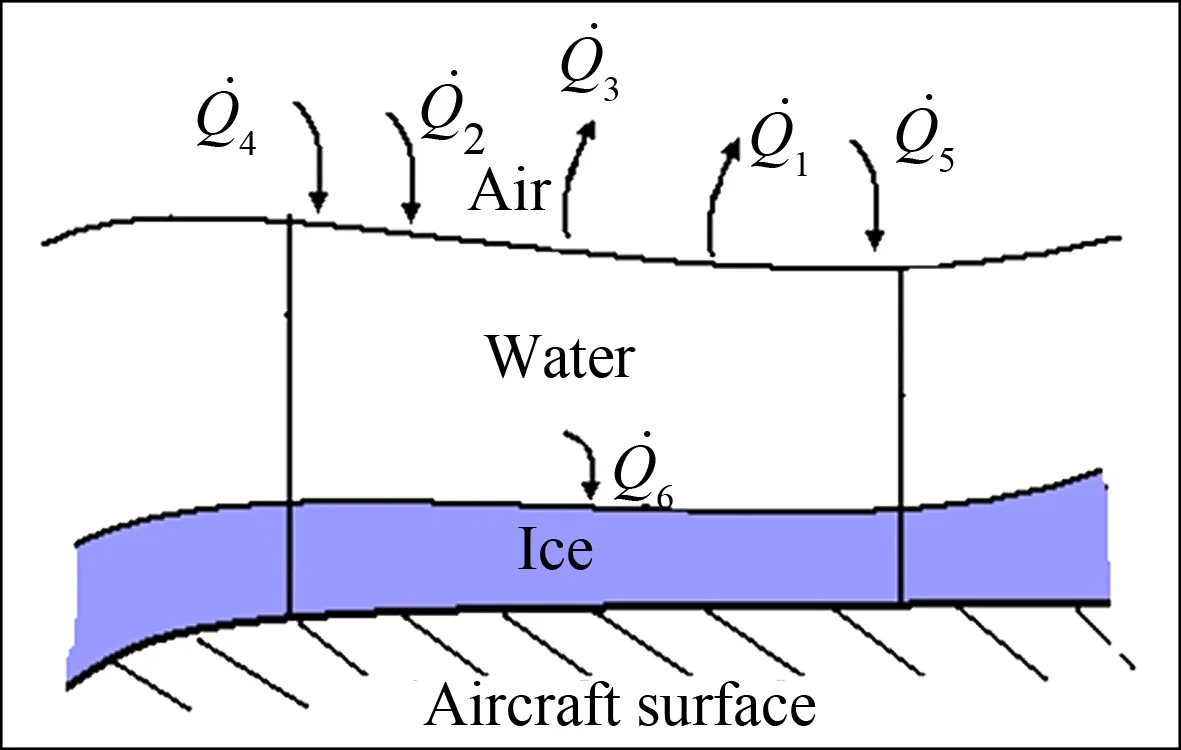
圖1 結冰表面控制體積內的能量傳遞

(2)

(3)

(4)

(5)

(6)

(7)

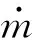
將式(2)～(7)代入(1)可得：

(8)

式中：T0為參考溫度，T0=273.15K;ci為冰的比熱;n為凍結比例，定義為表面某控制體積中凍結成冰的水質量與進入該控制體積的所有水質量的比值。對于明冰，將表面溫度Ts=T0=273.15K代入式(8)并進行變換，可得到凍結比例表達式：

(9)

通常將式(9)寫成如下形式：

(10)

其中，φ為水滴能量傳遞勢，其表達式為：

(11)

θ為空氣能量傳遞勢，可寫成：

(12)

b為相對熱因子，定義為：

(13)

式中：LWC為液態水含量，β為收集系數。

凍結比例n，相對熱因子b，空氣、水滴的能量傳遞勢θ和φ，是基于Messinger模型得到的結冰熱力學相似參數，其中n和b均為無量綱參數，θ和φ則具有溫度的量綱。為了使結冰過程的熱力學特性相似，不同研究者定義了不同的相似參數及組合。AEDC的準則中有2個相似參數，分別為凍結比例n和水滴能量傳遞勢φ，相似性要求為

nm=nf

(14)

(15)

其中下標“m”和“f”分別代表模型結冰的試驗條件和全尺寸物體的參考結冰條件。ONERA的準則定義了2個相似參數，分別為熱相對因子b和凍結比例n，其熱力學過程的相似要求除了滿足方程(14)，還需滿足

bm=bf

(16)

2 考慮相變時間效應相似參數的推導

Messinger模型只從宏觀上考慮了結冰過程的能量平衡，不能刻畫結冰相變過程的傳熱學效應，尤其是忽略了相變的時間效應，基于該模型得到的相似準則在模擬明冰和混合冰方面始終存在不足。為此，本文嘗試從傳熱學的角度推導相變的相似參數。

根據來流條件的不同，當空氣中的過冷水滴撞擊到飛機表面時，通常會出現表面無液膜和液/固共存的2種結冰現象，前者稱為干模式結冰，后者稱為濕模式結冰。由于干模式可以看作濕模式的特殊情況，為了使推導具有通用型，以濕模式作為推導對象，如圖2所示 ，一維相變傳熱過程可描述如下[14,16]：

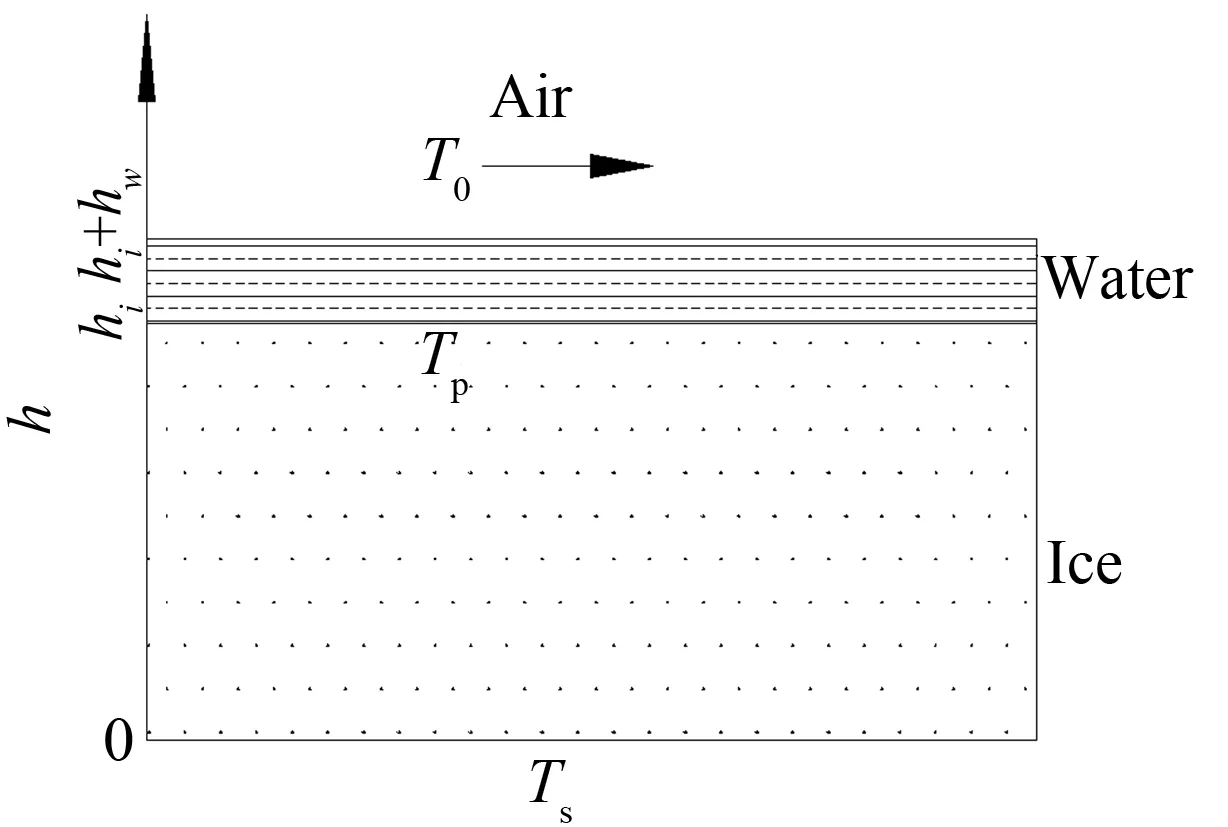
圖2 結冰表面物理模型

固相區和液相區：

(17)

(18)

液/固相界面：

(19)

(20)

液/氣相界面：

(21)

式中：qc為氣流與表面的對流換熱；qe為蒸發帶走的熱量；qw為撞擊在表面的水滴自身攜帶的能量；qa為氣動加熱量；qk為撞擊在表面的水滴所具有的動能。

質平衡方程：

(22)

若將固、液相區的導熱視為準穩態過程，對(17)和(18)式進行積分，并根據邊界條件(20)和(21)式可得冰層和水膜的溫度分布分別為

(23)

(24)

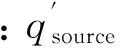
將冰層生長過程分為液膜出現之前的干模式和液膜出現后的濕模式[14]，并定義從干模式轉變為濕模式的臨界時間為tc，對質平衡方程(22)在濕模式區間(tc-t)進行積分得：

(25)

則濕模式階段，水膜、冰層厚度與時間的關系為：

(26)

根據式(23)、(24)及液/固相界面能量方程(19)可得：

(27)

將(26)代入(27)式，即可獲得冰層厚度隨時間的變化關系：

(28)

在水膜出現的臨界點，有：

(29)

可得從干模式轉變為濕模式的臨界冰層厚度為：

(30)

本文認為，對于2種相似的結冰，干模式轉變為濕模式的無因次臨界冰層厚度應相等，為此引入新的相似參數CT(臨界厚度，CriticalThickness)，定義

(31)

為相似參數，表征的是干模式轉變為濕模式的無因次臨界冰層厚度，其中L為特征尺寸，則相似性要求為

(32)

3 試驗參數的確定方法

對于結冰試驗，需要確定的試驗參數共有7個，包括模型尺寸Lm、速度Vm、壓力pm、水滴直徑dm、液態水含量LWCm、結冰時間tm和溫度Tm，而現有的結冰試驗相似準則共有4個約束方程，因此在選取試驗參數時可以自由指定3個，通常根據結冰風洞試驗段大小指定試驗模型尺寸，再自由給定速度和壓力，其余試驗參數則通過計算獲得。以AEDC的相似準則為例，其確定試驗參數的公式為[3]：

Lm=[selectedbyuser]

Vm=[selectedbyuser]

pm=[selectedbyuser]

(33)

在實際應用中，通常以Weber數相等作為試驗速度選取的條件，即：

(34)

將新的相似參數CT引入，結合式(32)和(34)進行數值迭代求解，可使得壓力與速度唯一確定，避免壓力與速度選取的隨意性。

4 相似參數的有效性評估

采用數值方法對本文提出的相似參數的有效性進行評估，數值評估的主要思路為，計算2個幾何相似且嚴格縮比翼型上的結冰，計算條件按新相似參數及式(33)確定的參數關系式進行選取。如果在2個翼型上得到的冰形也具有與物體幾何尺寸同樣的縮比比例，則認為相似參數是有效的。本文分別選用NACA0012翼型和某超臨界翼型進行了數值仿真評估，數值計算的方法參見文獻[3]。

4.1NACA0012翼型

NACA0012翼型的參考結冰條件為：特征尺寸1m，速度72m/s,壓強101 325Pa，溫度-7℃，水滴直徑20μm，液態水含量0.5g/m3，結冰時間25min,由該條件計算的CT數為0.0069。表1給出的是參考結冰條件以及按照式(32)、(33)和(34)所計算的1/2縮比模型的試驗條件，表中“Reference”代表參考結冰條件，“Sacling”代表縮比的試驗條件。

表1 NACA0012翼型參考結冰條件

圖3給出的是參考狀態和縮比狀態下，翼面水滴收集率分布曲線，可以看到，除了在下翼面撞擊極限附近有微小差別，2種狀態的水滴收集率分布均保持一致；圖4顯示的是將參考條件和縮比條件對應的冰形歸一化之后的對比，可以發現，無論結冰的范圍、冰的厚度和冰角位置等，二者均保持一致，說明按照表1所給出的參數進行結冰，能夠保證參考條件和試驗條件具有一致的結冰外形。

圖3 試驗條件與參考條件水滴收集率對比(NACA0012 翼型)

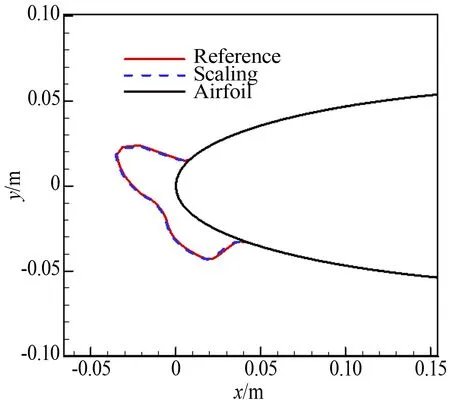
圖4 試驗條件與參考條件結冰外形對比(NACA0012 翼型)

4.2 超臨界翼型

本文研究所采用的超臨界翼型源自某型運輸機機翼剖面，如圖5所示，該翼型弦長3m，最大厚度0.35m。

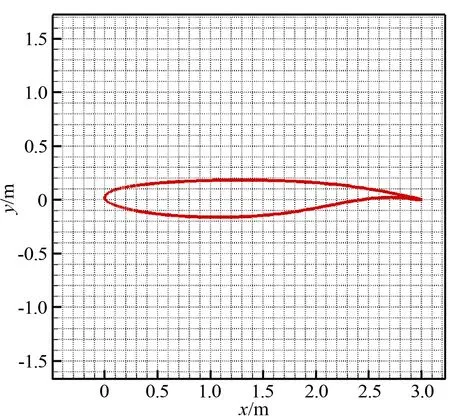
圖5 計算采用的超臨界翼型(超臨界翼型)

超臨界翼型的參考結冰條件為：特征尺寸3m，速度116m/s,壓強84 606Pa，溫度-8.8℃，水滴直徑20μm，液態水含量0.54g/m3，結冰時間22.5min,由該條件計算的CT數為0.001，表2給出的是參考結冰條件及其對應的1/2縮比模型的試驗條件。

表2 超臨界翼型參考結冰條件

圖6給出的是水滴收集率分布曲線的對比，計算顯示縮比條件與參考條件下的水滴收集率一致，由于水滴收集率主要決定于來流速度、水滴直徑和空氣密度，雖然縮比條件的水滴直徑比參考條件小會導致水滴收集率降低，但是縮比條件中速度、密度的增加，以及模型尺寸的減小又會帶來水滴收集率的增加，綜合效應使得縮比條件與參考條件下的水滴收集率達到了一致。

圖7給出的是結冰外形對比，可以看到：翼面形成的是典型明冰；2種條件對應的結冰在上翼面結冰極限以及駐點處的厚度完全相同；下翼面的結冰極限有微小差異，縮尺條件的結冰極限略小于參考條件；翼面下方的冰角保持一致，翼面上方的冰角有細微差異，縮尺條件的冰角比參考條件的冰角略大。總的說來，2種冰形在翼面的分布范圍相同，冰的生長趨勢和冰形輪廓總體上是一致的。說明按照表2的縮尺結冰條件，能夠得到與參考冰形相似的結冰。

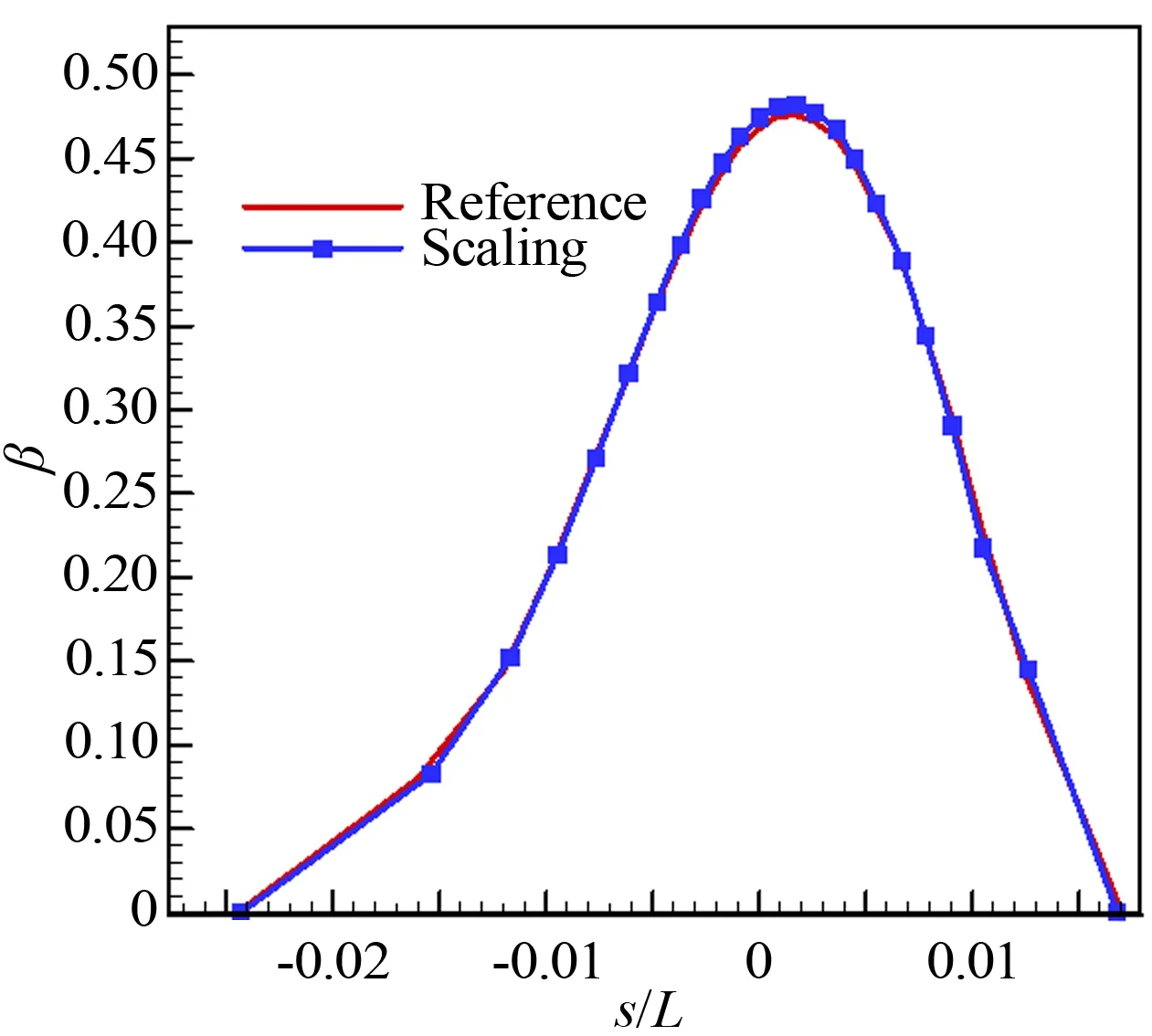
圖6 試驗條件與參考條件水滴收集率對比(超臨界翼型)

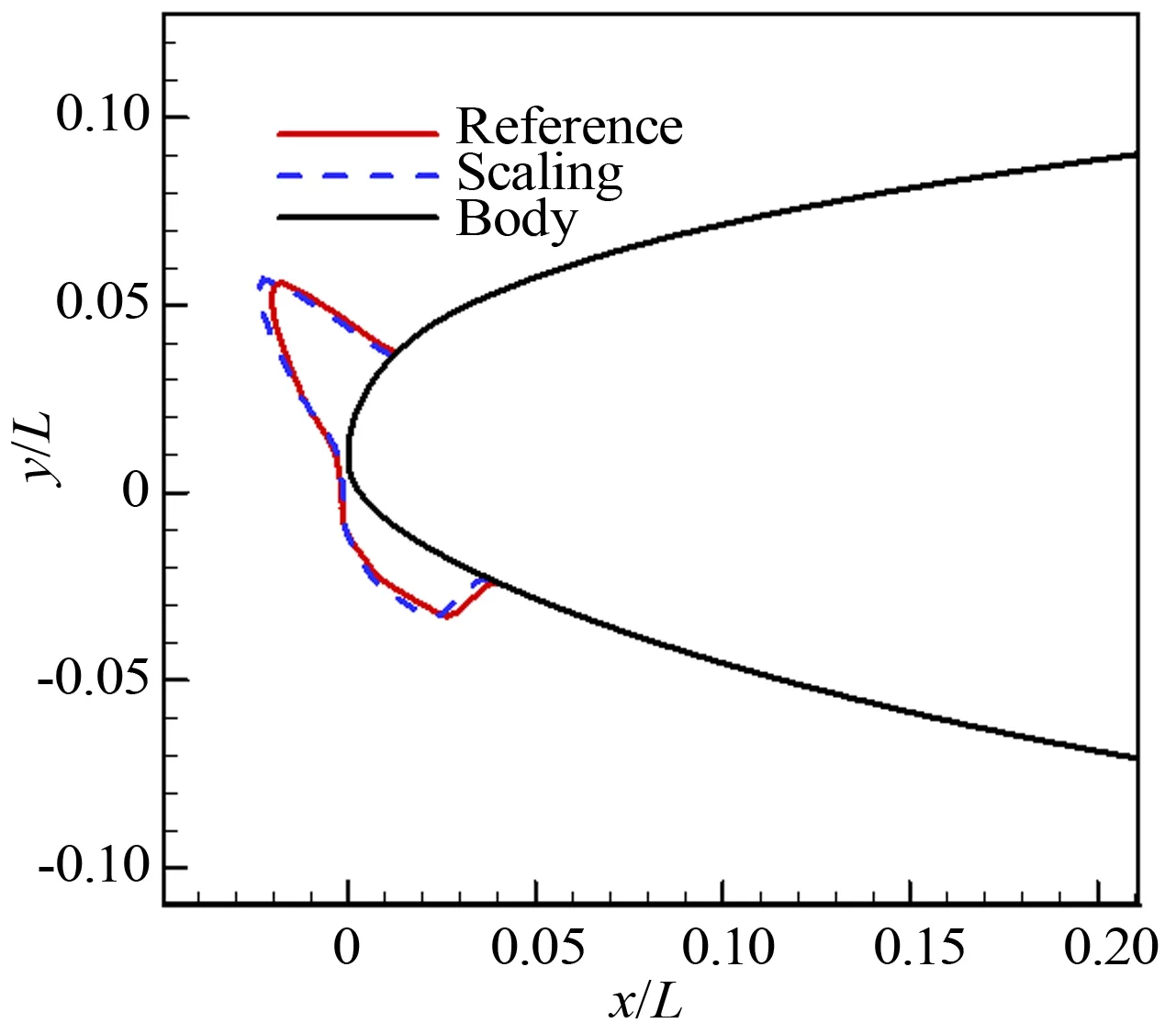
圖7 縮尺條件與參考條件結冰外形對比(超臨界翼型)

5 結論

基于結冰過程的傳熱模型，提出了一個考慮相變時間效應的結冰試驗相似參數CT，并采用數值方法進行了驗證評估，得到如下結論：

(1)從結冰相變的傳熱學過程所推導的新相似參數，與基于Messinger結冰熱力學模型所推導的相似參數有明顯區別，其顯著特征是考慮到了結冰的干模式和濕模式，體現了相變的時間效應；

(2)通過將新的相似參數引入到現有結冰試驗相似準則中，結合等Weber數的試驗速度選取原則，可使得試驗壓力與速度唯一確定，避免了壓力與速度選取的隨意性;

(3)數值仿真評估結果說明，采用本文提出的相似參數及相應的試驗參數確定方法，能夠得到與參考條件一致的水滴收集率和結冰，初步說明新相似參數的是有效的;

(4)飛機結冰,尤其是包含濕模式的結冰，涉及到復雜環境下的空氣和液態水流動、傳熱傳質與相變，本文工作是對濕模式結冰精確模擬試驗理論的初步探索，雖然初步結果讓人滿意，但還需進一步深入和完善，尤其需要開展大量的實驗驗證工作。

[1]CebeciT,KafyekeF.Aircrafticing[J].AnnualReviewofFluidMechanics, 2003, 35:11-21.

[2]BraggMB,BroerenAP,BlumenthalLA.Iced-airfoilaerodynamics[J].ProgressinAerospaceSciences, 2005, 41(5):323-362.

[3] 易賢. 飛機積冰的數值計算與積冰試驗相似準則研究[D]. 綿陽：中國空氣動力研究與發展中心,2007.

YiX.Numericalcomputationofaircrafticingandstudyonicingtestscalinglaw[D].Mianyang:ChinaAerodynamicsResearchandDevelopmentCenter, 2007.

[4]CharpinF,FassoG.Icingtestinginthelargemodanewing-tunnelonfull-scaleandreducedscalemodels[R].NASA-TM-75737, 1979.

[5]RuffGA.Analysisandverificationoftheicingscalingequations[R].AEDC-TR-85-30, 1985.

[6]RuffGA.Verificationandapplicationoftheicingscalingequations[R].AIAA-86-0481,1986.

[7]AndersonDN.Rime-,mixed-,andglaze-icedevalutionsofthreescalinglaws[R].AIAA-94-0718, 1994.

[8]AndersonDN.Methodsforscalingicingtestconditions[R].AIAA-95-0540, 1995.

[9]AndersonDN.Furtherevaluationoftraditionalicingscalingmethods[R].AIAA-96-0633, 1996.

[10]易賢, 朱國林, 桂業偉. 一種改進的積冰試驗相似準則及其評估[J]. 實驗流體力學, 2008, 22(2): 84-87.

YiX,ZhuGL,GuiYW.Modificationandevaluationofanicing

scalinglaw[J].JournalofExperimentalsinFluidMechanics, 2008, 22(2): 84-87.

[11]AndersonDN.Manualofscalingmethods[R].NASA/CR-2004-212875, 2004.

[12]杜雁霞, 桂業偉, 肖春華, 等. 飛機結冰過程的液/固相變傳熱研究[J]. 航空動力學報, 2009, 24(8): 1824-1829.

DuYX,GuiYW,XiaoCH,etal.Investigationonsolid-liquidphasechangeheattransferofaircrafticing[J].JournalofAerospacePower, 2009，24(8)：1824-1829.

[13]MessingerBL.Equilibriumtemperatuerofanunheatedicingsurfaceasafunctionofairspeed[J].JournaloftheAeronauticalSciences, 1953, 20(1): 29-42.

[14]MyersTG.Anextensiontothemessingermodelforaircrafticing[J].AIAAJournal, 2001, 39(2): 211- 218.

[15]易賢, 桂業偉, 朱國林. 飛機三維結冰模型及其數值求解方法[J]. 航空學報, 2010, 31(11): 2152-2158.

YiX,GuiYW,ZhuGL.Numericalmethodofathree-dimensionaliceaccretionmodelofaircraft[J].ActaAeronauticaetAstronauticaSinica, 2010, 31(11): 2152-2158.

[16]DuYX,GuiYW,XiaoCH,etal.Investigationonheattransfercharacteristicsofaircrafticingincludingrunbackwater[J].InternationalJournalofHeatandMassTransfer, 2010, 53: 3702-3707.

(編輯：楊 娟)

An icing scaling parameter with the effects of phase change time

Yi Xian*, Zhou Zhihong, Du Yanxia, Zhu Guolin

(State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China)

The icing wind tunnel test is the main method for the aircraft icing research. The icing scaling law is the theoretical foundation of an icing wind tunnel test. To overcome the disadvantage of current icing scaling method in glaze and mixing ice simulation, a new scaling parameter,CT, is proposed in this paper based on the analysis of heat transfer in icing process. This parameter differs significantly from the scaling parameters originated from Messinger’s thermodynamic model for it take the effects of the phase change time into account. Introducing CT into the traditional scaling law can effectively avoid the randomness in selecting the test pressure and speed. The new parameter has been evaluated with numerical method based on the NACA0012 airfoil and a supercritical airfoil. The results show that on the two airfoils, both the ice shapes and the droplet collection efficiency under the reference icing conditions agree with those under the selected test conditions, which indicates that the parameter is feasible. The research work has good reference value for improving the accuracy of experimental simulation of glaze or mixing ice.

aircraft icing;icing wind tunnel;icing scaling law;icing model;heat transfer;phase change

1672-9897(2016)02-0014-06

10.11729/syltlx20160016

2015-12-22;

2016-02-02

國家自然科學基金(11172314，11472296), 國家重點基礎研究發展計劃(2015CB755800)

YiX,ZhouZH,DuYX,etal.Anicingscalingparameterwiththeeffectsofphasechangetime.JournalofExperimentsinFluidMechanics, 2016, 30(2): 14-19. 易 賢, 周志宏, 杜雁霞, 等. 考慮相變時間效應的結冰試驗相似參數. 實驗流體力學, 2016, 30(2): 14-19.

V211.3,V244.1+5

A

易 賢(1977-)，男，四川成都人，博士,副研究員。研究方向：空氣動力學與飛機結冰的交叉領域。通信地址：四川綿陽中國空氣動力研究與發展中心計算所(621000)。E-mail:yixian_2000@163.com

*通信作者 E-mail: yixian_2000@163.com