天平校準不確定度的一種評估方法

劉春風, 熊 琳, 劉家驊, 李海燕

(中國航天空氣動力技術研究院, 北京 100074)

天平校準不確定度的一種評估方法

劉春風, 熊 琳*, 劉家驊, 李海燕

(中國航天空氣動力技術研究院, 北京 100074)

建立了一套完整的天平校準不確定度評估流程：單獨評估校準系統的不確定度、基于檢驗載荷的殘差,通過偏差極限和精度極限評估其它各誤差源引入的不確定度、合并得到校準不確定度結果。以BCS-100天平校準系統為例,選擇天平TG624C重復校準7次,實現了該評估方法。評估結果表明：(1)天平安裝的滾轉角和加載時天平的角位移,二者引入的不確定度為主要分量,應作為技術改造的重點；(2)Q、Z和My3個小量單元,受Y和Mz2個大量的干擾,其不確定度值稍大；(3)精度極限相比于偏差極限要小很多。建立的整套評估方法對于其他校準系統也是通用的。

不確定度；校準系統；偏差極限；精度極限；重復

0 引 言

風洞天平是風洞測力試驗中最重要的測量裝置,用于測量飛行器模型上氣動載荷的大小和作用點。一桿天平自設計、加工和貼片后,在投入風洞試驗之前,必須進行地面靜態校準,得到天平載荷輸入和信號輸出的對應關系,即天平公式。靜態校準的質量直接決定了風洞試驗數據結果的質量。為有效表征和衡量靜態校準的質量,在天平完成校準后,需給出天平校準的不確定度。除此之外,天平校準不確定度是風洞試驗不確定度的主要來源[1],合理評估天平校準不確定度,也是系統分析風洞試驗氣動力數據不確定度的前提。

各行業的不確定度評估工作,歷來難點不在于缺乏好的評估方法,難點在于研究人員和工程設計人員如何在應用這些方法的過程中保持一致性和規律性[2],即不確定度評估的標準化。對于天平校準不確定度的評估,傳統方法一直是將校準的實驗標準偏差作為不確定度的近似結果[3-6]。近年來,國內外各氣動機構在天平校準不確定度的評估上逐漸開展了一些研究工作。國內的《風洞應變天平規范》闡述了校準不確定度有5個來源[7]。國外的天平校準不確定

度評估主要是基于風洞試驗的不確定度評估思想[8-10]。國內外已有的研究工作對天平校準不確定度的認識在不斷提高。但各機構的評估方法一般只針對各自的天平校準,互相之間差異巨大。除此之外,在評估的具體細節中,仍有很多問題模糊不清,目前為止還沒有全面系統的評估實例。這說明天平校準不確定度的評估與實現標準化還有很遠的距離。

天平校準不確定度的評估要實現標準化有困難,一是由于各校準機構所應用的校準系統千差萬別,而校準系統的不確定度是最終天平校準不確定度的重要組成部分。大多數方法都是將校準系統與其它各因素引入的不確定度一并展開評估,這導致了各結構的評估方法均只適用于各自的天平校準,無法通用；二則是天平校準的整個過程中誤差源眾多,層次關系復雜。在評估過程中,經常出現某些誤差源引入的不確定度被重復計算或被忽略的情況。基于此2個主要問題,本文著眼于天平校準不確定度評估的標準化,將校準系統引入的不確定度單獨進行評估。除此之外,為合理歸納各誤差源引入的不確定度并體現其作用方式,將誤差源頭分成隨機誤差和系統誤差2部分,并將其引入的不確定度歸類為精度極限和偏差極限。

1 評估方法概述

風洞天平的校準,誤差來源眾多。它主要的誤差來源有幾方面：(1)校準系統。主要是載荷發生裝置、載荷傳遞裝置因加工、安裝引入的誤差；(2)天平自身。一是天平的彈性元件存在滯后、蠕變和非線性等缺陷,二是應變計存在溫漂、零漂和非線性等現象；(3)數據采集系統。數采系統受分辨率、噪聲和熱效應因素等的影響,會存在測量與控制誤差；(4)數據處理方法。主要是天平校準載荷表的編制方法、天平公式的求解方法等引入的系統誤差。天平校準不確定度的評估,需要從上述誤差源出發,建立的評估方法應能夠體現各誤差源及其作用方式。

對于校準系統,其引入的不確定度將單獨展開評估。對于天平自身、數采系統和數據處理方法等引入的不確定度,由于校準過程中各因素同時作用,且校準工作者能夠得到的信息只有天平讀數及其它校準數據,所以若單獨評估各項,是非常困難的。比較實際的做法是有效利用校準數據,尤其是檢驗載荷的殘差,它是各種誤差綜合作用的結果,適合用來表征除校準系統外其它誤差源引入的不確定度。

為合理體現其它誤差源頭的作用方式,可基于檢驗載荷的殘差,從精度極限和偏差極限2部分具體展開評估工作：關于精度極限,考察精度極限最直接有效的方式就是重復。即重復加載同一檢驗載荷,通過各次檢驗載荷殘差的標準偏差進行表征；關于偏差極限,可取各次檢驗載荷的殘差均值直接進行表征。

2 評估流程

2.1 校準系統的不確定度評估

校準系統安裝完畢后,由于安裝誤差的存在,作用于天平上的實際載荷是存在誤差的,并且該誤差是恒定的。在該安裝狀態下重復校準天平時,校準系統的不確定度,即實際載荷的不確定度,是最終天平校準不確定度的一部分。

校準系統的不確定度評估,首先需根據校準系統的工作方式,分析校準系統可能引入誤差的輸入量,并逐一評估各輸入量的不確定度值。然后列出實際載荷與各輸入量的函數關系,即載荷的數學模型。最后按照不確定度傳播定律,計算得到實際載荷的不確定度。

2.1.1 分析輸入量

對于一般的天平校準系統,載荷來源是砝碼或其它力發生裝置,最終的輸出量是天平上的實際載荷。在載荷傳遞過程中,實際載荷的具體值,會受到校準系統各輸入量的誤差影響。不同的天平校準系統工作方式各不相同,決定了其輸入量存在差別,各機構需要針對各自的校準系統單獨展開分析。

圖1所示為某高超聲速風洞配套的BCS-100天平校準系統。被校準天平通過支桿連接至基準臺上,通過基準臺實現被校準天平的定位和調整。專門設計了加載頭為天平提供各分量載荷的加載,安裝時將加載頭連接至天平上,后連接鋼絲,鋼絲經過滑輪連接砝碼盤。校準時向砝碼盤上施加砝碼,用砝碼的自重實現各個載荷分量的模擬。關于該校準系統的詳細信息,可查閱參考文獻[11]。

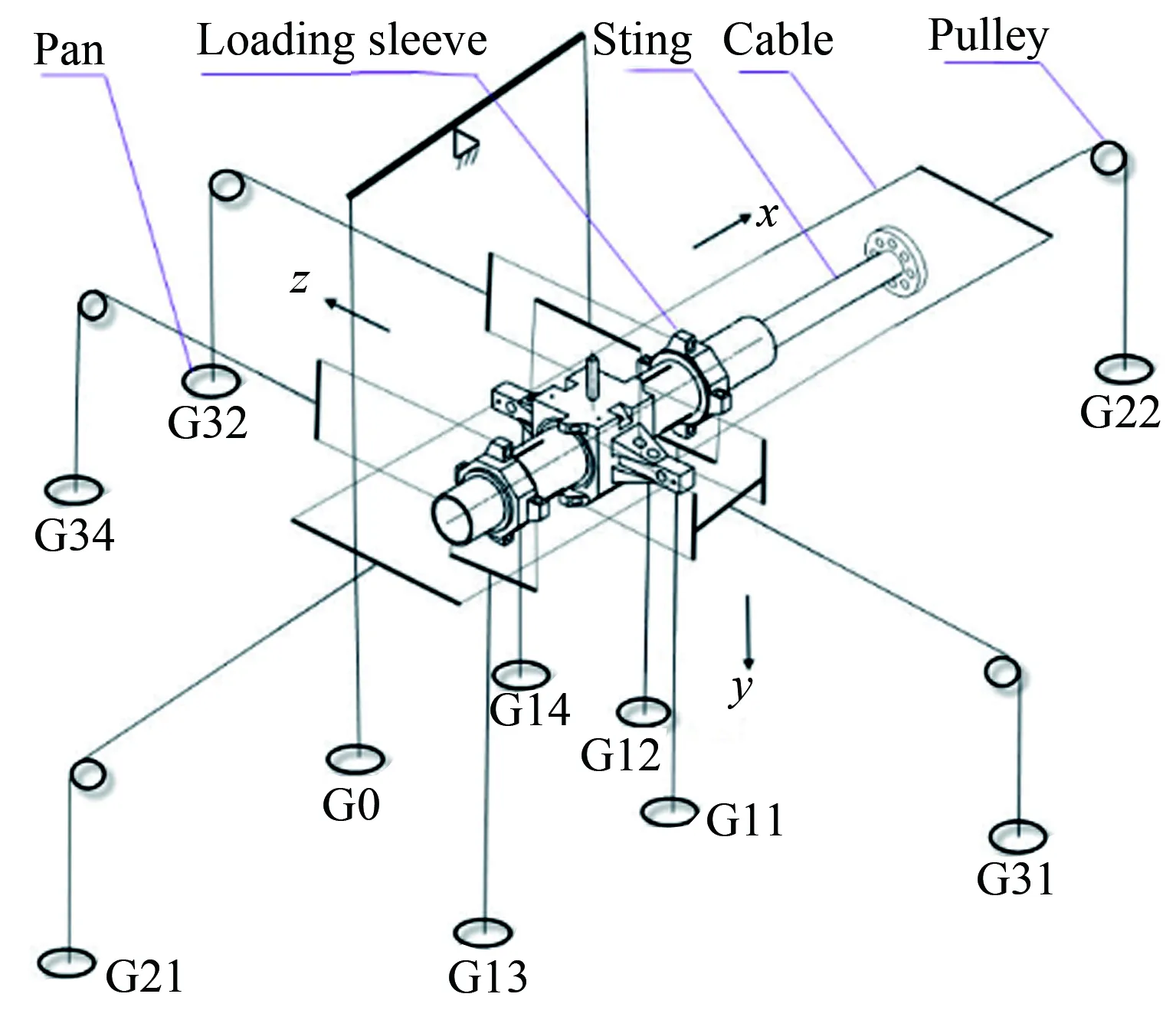
圖1 BCS-100校準系統的示意圖

對于該天平校準系統,引入誤差的輸入量主要有天平安裝的滾轉角、加載頭安裝角、滑輪安裝位置和加載頭的加載點位置等,具體如表1所示。關于天平線位移及各位置參數的正方向,與圖1所示坐標軸的正方向一致；各角度的正方向,與傳統俯仰角、偏航角和滾轉角的正方向定義一致。

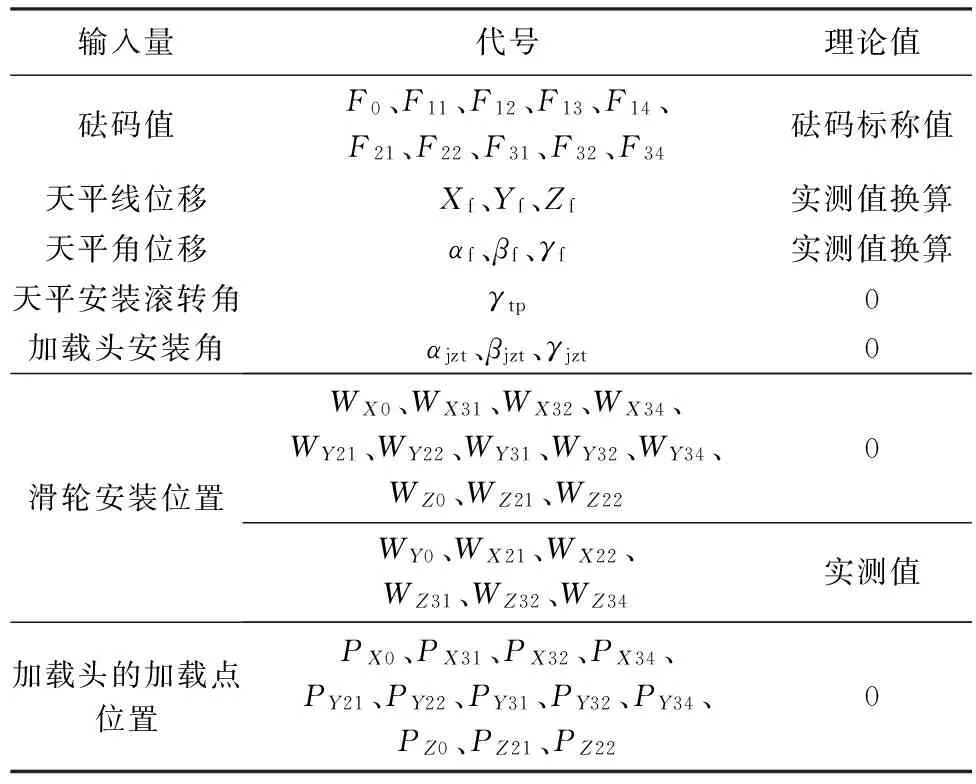
表1 BCS-100校準系統的輸入量

針對校準系統的各輸入量,可根據不確定度的A類或B類評定手段,逐一評估其不確定度值。

2.1.2 列出數學模型

一般來說,校準系統的輸入量很多,如何有效組織各輸入量是建立數學模型的關鍵,這也是不確定度分析的難點。目前有些研究機構認識到單獨評估校準系統不確定度的必要性[9],但還未見任何評估實例。本文提出從載荷來源的空間分解方式出發,逐一分析各輸入量對實際載荷的作用方式并得到函數關系,最后匯總各載荷源,建立最終的數學模型。

實際載荷的數學模型,不等同于實際載荷測量結果的計算公式,即使有些因素對載荷結果的影響很小,但對于測量不確定度來說是必須考慮的。如校準系統存在理論值為0的各輸入量Xi,但由于安裝或工作過程中的其它原因,各輸入量會存在誤差并引入不確定度,必須將其誤差的修正值δXi加入數學模型。

以BCS-100校準系統的阻力Q為例。首先分析載荷源G31對阻力Q的影響,圖2所示為砝碼值F31在xz平面對Q的干擾。G31滑輪的x向位置WX31存在安裝誤差δWX31、加載頭上的加載點位置PX31存在加工誤差δPX31,在與天平x方向的線位移Xf共同作用下,砝碼值F31會對Q產生干擾：

(1)

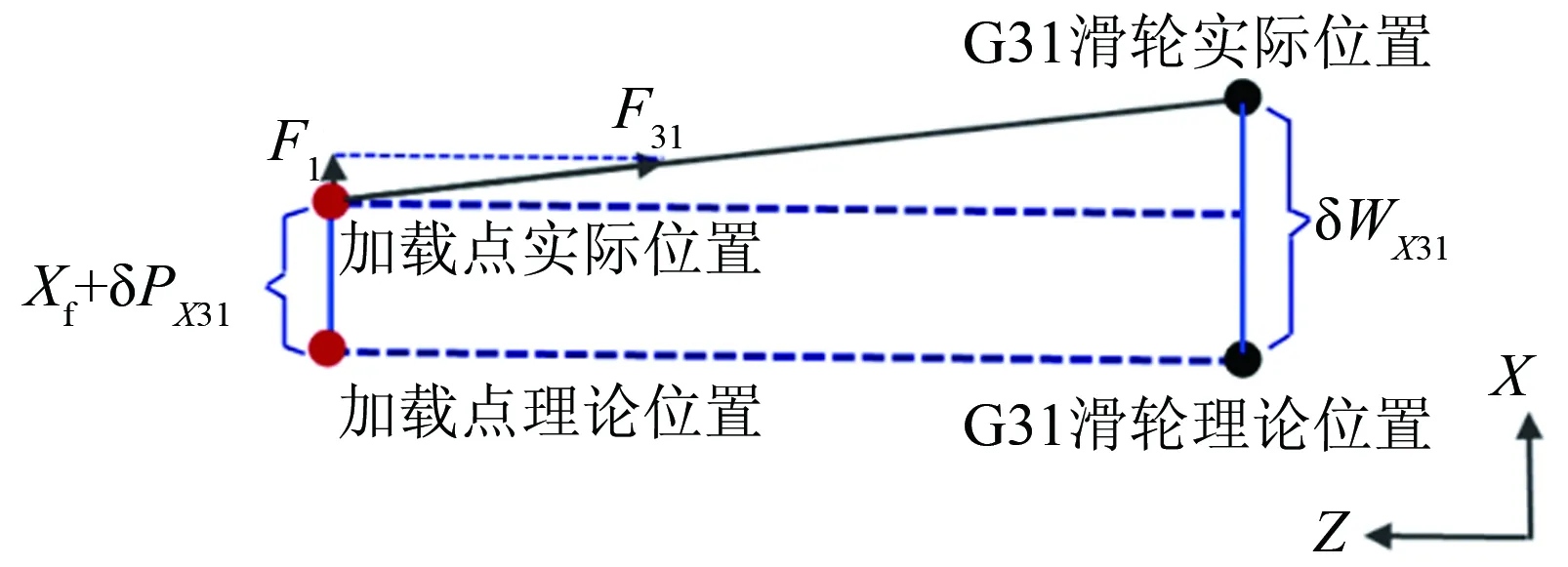
圖2 xz平面內砝碼值F31對Q的干擾

當加載頭存在偏航角的安裝誤差δβjzt時,在與天平的角位移βf共同作用下,式(1)變化為：

(2)

式(2)中F31的矢量方向在xz平面內。實際上,由于高度y方向的各輸入量誤差,F31不可能完全位于xz平面內。圖3所示為F31向xz平面上的投影示意圖。滑輪G31的y向位置WY31存在安裝誤差δWY31、加載頭上的加載點位置PY31存在加工誤差δPY31,在與天平y方向的線位移Yf共同作用下,砝碼值F31在xz平面上的投影可表示為：

(3)

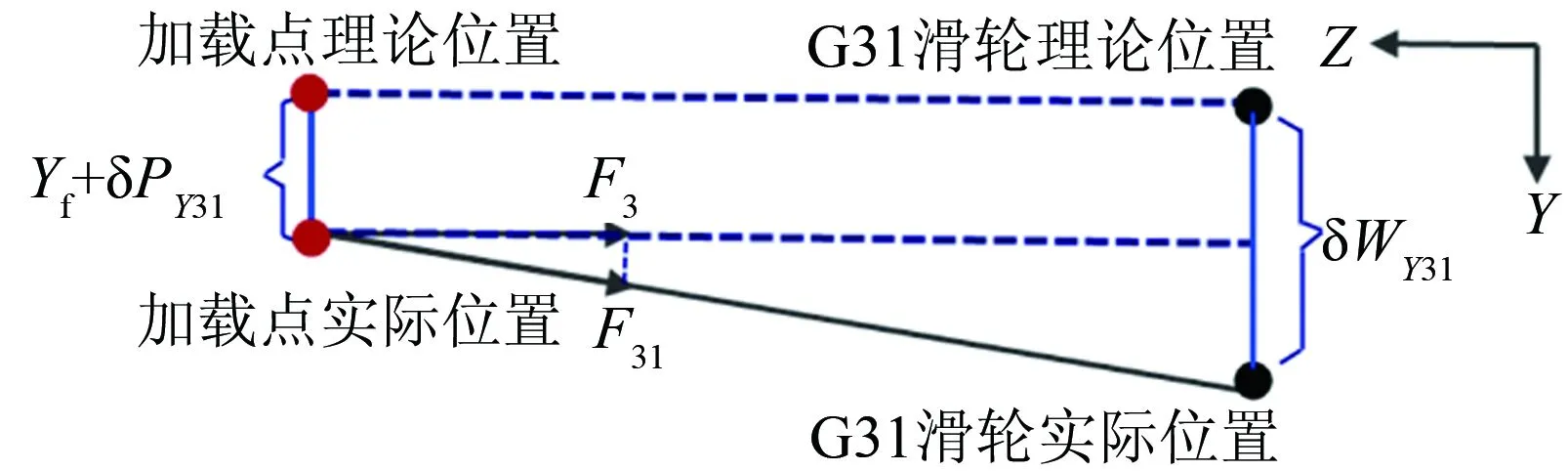
圖3 砝碼值F31向xz平面的投影

當天平存在滾轉角的安裝誤差δγtp,并且加載頭存在滾轉角的安裝誤差δγjzt時,在與天平的角位移γf共同作用下,式(3)變化為：

(4)

綜合式(2)和(4),得到載荷源G31與Q的函數關系為：

(5)

同理,可依次分析其它各載荷源對Q的影響方式,篇幅所限,不再敘述。匯總各載荷源,得到Q的數學模型為：

(6)

2.1.3 合成標準不確定度

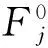
(7)

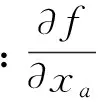
式(7)只是其中一組檢驗載荷的結果,對各組檢驗載荷Fj的結果進行方根和處理,作為校準系統的不確定度結果。

(8)

2.2 其他誤差源引入的不確定度評估

天平自身、數采系統、數據處理等其它因素引入的不確定度,分成精度極限和偏差極限2部分展開評估。精度極限,是各隨機誤差引入的不確定度的綜合；偏差極限,是各系統誤差引入的不確定度的綜合。在評估時應避免隨機誤差與系統誤差混纏在一起,考察二者最直接有效的方式就是開展重復的天平校準。關于重復的方式,各次校準應單獨加載擬合載荷和檢驗載荷,單獨計算各次的天平公式和檢驗載荷殘差。由于校準系統的安裝誤差引入的不確定度,已通過校準系統的不確定度得到了有效考察。所以,重復校準時不再拆裝校準系統,保證同一安裝狀態。

重復開展N次天平校準后,直接取各次天平校準的檢驗載荷殘差均值,表征偏差極限；計算各次天平校準的檢驗載荷殘差的標準差,處理后表征精度極限。此時得到的偏差極限體現了天平自身、數據處理方法共同引入的系統誤差；得到的精度極限則體現了

除校準系統之外全部流程引入的隨機誤差。二者的具體計算流程如下：

2.2.1 偏差極限

天平在各次校準完成后,依次擬合得到天平公式[Ci],其中,i為重復校準的次數；加載檢驗載荷可得到天平讀數[Rij],計算反算檢驗載荷Fij為：

(9)

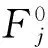
(10)

針對N次重復的天平校準,可得到殘差εij的均值,作為該組檢驗載荷的偏差極限估值。

(11)

對各組檢驗載荷的偏差極限估值進行方根和處理,作為校準的偏差極限結果。

(12)

2.2.2 精度極限

針對各檢驗載荷組Fj,計算N次重復校準時殘差εij的標準差,即

(13)

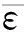
(14)

對各組檢驗載荷的精度極限估值進行方根和處理,作為校準的精度極限結果。

(15)

2.3 評估結果的合并

評估得到校準系統的不確定度,并通過偏差極限和精度極限得到其它誤差源引入的不確定度后,對三

者進行合并,作為最終的校準不確定度結果。

(16)

3 評估結果與分析

基于BCS-100校準系統,選擇某高超聲速風洞的應變天平TG624C,運用上述方法開展了7次重復校準。圖4所示為各載荷單元在各次天平校準中的檢驗載荷殘差數據。

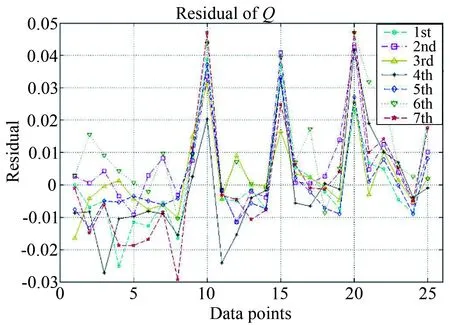
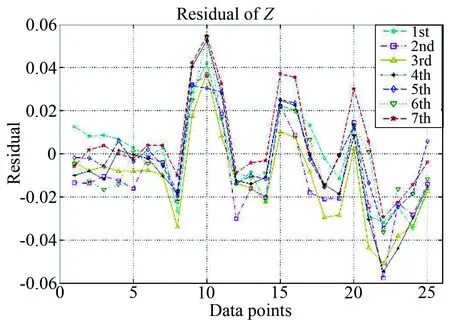
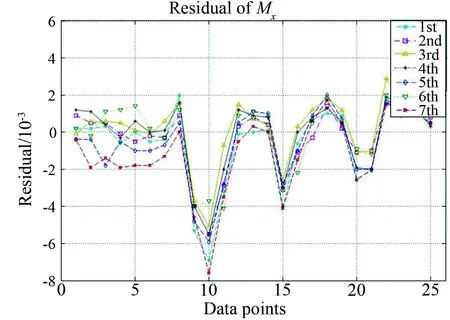
圖4 各次天平校準檢驗載荷的殘差

3.1 校準系統的評估結果

運用上述的評估方法,首先評估得到校準系統的不確定度,并額外計算了校準系統的各不確定度分量,及各不確定度分量在校準系統不確定度中的所占比重。表2列出了3個力分量的相關結果。

通過表2的數據結果可以看出,只有個別輸入量引入的不確定度占絕對優勢,其余大部分不確定度分量非常小。總體上講,天平安裝的滾轉角和加載時天平的角位移,二者引入的不確定度為主要分量,應作為該校準系統技術改造的重點；加載頭的加載點位置和砝碼引入的不確定度相比之下非常小,可以忽略不計。

通過與滑輪相關的不確定度比重可以發現：總體上滑輪引入的不確定度很小,并且產生載荷的生力滑輪,不確定度分量基本為0,相比之下其它滑輪的干擾引入的不確定度稍大。以阻力Q為例,阻力Q靠G21和G22產生阻力,但G21和G22引入的不確定度基本為0,滑輪G31、G32、G34沿X向的偏移會產生額外的阻力分量,其引入的不確定度則相對要大很多。

3.2 綜合評估結果

表3所示為該天平的校準載荷及校準不確定度的綜合評估結果。

通過表3的數據結果可以看出：Y和Mz的不確定度的相對值較小,Q、Z和My3個單元的不確定度相對較大。這歸結于Y和Mz作為大量,其它載荷分量對其造成的干擾,相對其本身很小；而Q、Z和My3個單元的不確定度來源主要是Y和Mz2個大量的干擾,這由表2中Q、Z的各不確定度分量也可以得到驗證。對于阻力Q,由于加載頭俯仰角αjzt和天平角位移αf的存在,使法向力Y在阻力Q上產生投影,是Q主要的不確定度來源；對于側力Z,天平滾轉角γtp的存在,使Y在Z上產生投影,是Z的主要不確定度來源。

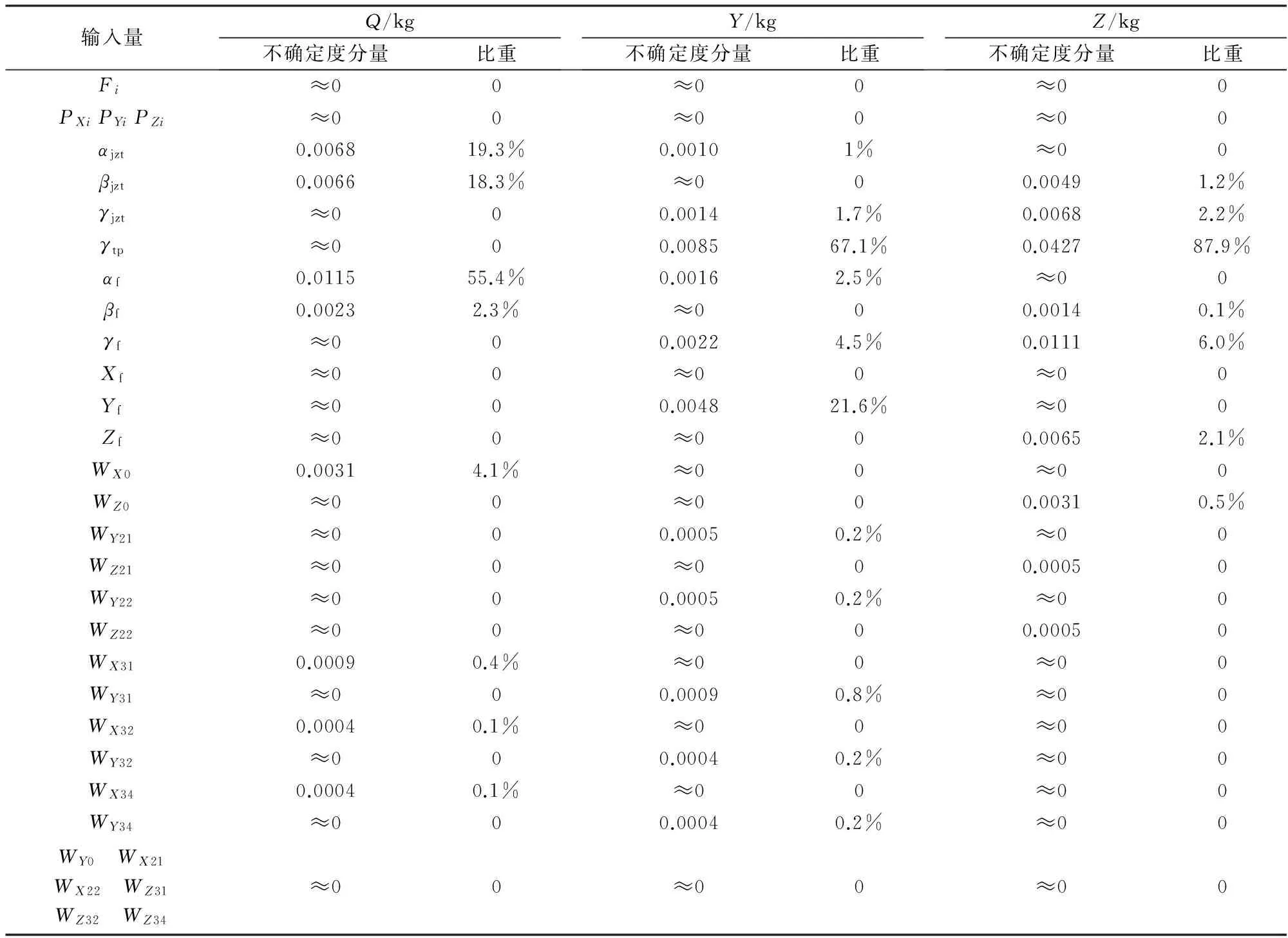
表2 阻力Q、升力Y、側力Z的不確定度分量及比重

表3 TG624C的校準不確定度評估結果

除此之外,通過表3可見精度極限相比于偏差極限要小很多,即該校準系統的安裝狀態固定后,天平校準不確定度的主要來源,是由天平校準各環節的系統誤差引入。

4 方法討論

本文天平校準不確定度的評估方法,單獨評估校準系統的不確定度,使得整套方法對于其它校準系統也可通用,這使實現天平校準不確定度的評估標準化變為可能。除此之外,對于校準系統之外的各誤差源引入的不確定度,采用精度極限和偏差極限的分類方式,可以直接看出隨機誤差與系統誤差的作用方式及比重結果。該分類方式在風洞試驗的不確定度評估中曾有過應用[2],對于處理復雜系統,該方法效果良好。

本文基于檢驗載荷評估了校準系統的不確定,并基于檢驗載荷評估了精度極限和偏差極限,所以該方法是基于檢驗載荷得到的。當檢驗載荷的載荷值及組數發生變化時,校準不確定度的數值結果也會發生變化。由于校準不確定度的評估,其中的目的之一是給風洞試驗的不確定度評估提供數據[2]。所以,為使評估結果更具有實際意義,應使檢驗載荷水平盡量接近風洞試驗載荷。

本文暫時未單獨計算數據采集系統和滑輪摩擦力引入的不確定度。二者引入的精度極限,都包括在最終的精度極限中。采集系統引入的偏差極限,對于天平校準來說,主要是量程誤差和截斷誤差2個因素,基于應用同樣采集系統的風洞試驗不確定度的評估經驗,發現其偏差極限很小,可以忽略；滑輪摩擦力引入的偏差極限,以BCS-100校準系統為例,目前還未能實現定量評估,該工作將在后續進行。

本文暫時未給出校準不確定度的自由度,一方面在于評估實際載荷的不確定度時,校準系統很多輸入量的不確定度評估是基于B類評定手段,在計算自由度時存在困難；另一方面,本文的評估方法整體上基于檢驗載荷的殘差,并非直接根據測量手段獲得,從原則上講自由度的概念變得牽強,必要性不大。

5 結 論

各機構的校準系統工作方式不同,決定了校準系統的輸入量互不相同,但本文的分析方法是通用的。研究工作可得到如下主要結論：

(1)單獨評估校準系統的不確定度,使評估方法實現通用變為可能；采用精度極限和偏差極限的分類方式,對于復雜系統的不確定度評估,效果良好。

(2)對BCS-100天平校準系統的TG624C天平進行評估,結果表明：天平安裝的滾轉角和加載時天平的角位移,是校準系統最大的不確定度分量；天平的大量Y和Mz的校準不確定度相對較小,Q、Z和My3個單元受Y和Mz這2個大量的干擾,不確定

度相對稍大；校準各環節的系統誤差是不確定度的主要來源。

(3)本文提出的天平校準不確定度的評估方法,其它校準機構也可應用,對天平校準不確定度評估的標準化工作具有廣泛的參考意義。

[1] Belter D L. Comparison of wind tunnel data repeatability with uncertainty analysis estimates[R]. AIAA-98-2714, 1998.

[2] Anon. Assessment of wind tunnel data uncertainty[R]. AIAA-S-071-1995, 1995.

[3] Mark E Kammeyer, Mathew L Rueger. Estimation of the uncertainty in internal balance calibration through comprehensive error propagation[R]. AIAA-2008-4029.

[4] John S Tripp. Strain gauge balance uncertainty analysis at NASA Langley-a technical review[R]. AIAA-94-2589, 1999.

[5] Maria L C C Reis, Olympio A F. A method for estimation of the calibration uncertainty of an external six-component wind tunnel balance[R]. AIAA-2002-2793.

[6] Maria L C C Reis, Olympio A F. Calibration uncertainty of an external six-component wind tunnel balance[R]. AIAA-2003-3884.

[7] 中國人民解放軍總裝備部. 風洞應變天平規范[S]. GJB 2244A-2011, 2011.

[8] Berng Ewald. The uncertainty of internal wind tunnel blalances: definition and verification[C]. The Third International Symposium on Strain-Gauge Balances, Darmstadt, 2002.

[9] R Bergmann, I Philipsen. Some contemplations on a proposed definition of uncertainty for balances[R]. AIAA-2010-4546.

[10] David Cahill. Balance Calibration Uncertainty Introduction to Discussion Standardization[C]. 6th International Symposium on Strain-Gage Balances, 2008.

[11] Xiong Lin, Gong Jian. A research on calibration method of obtaining body fixed coordinate system coefficients matrix using non-repositioning calibration system[C]. 9th International Symposium on Strain-Gage Balances, 2014.

[12] 中國人民解放軍總裝備部. 測量不確定度的表示及評定[S]. GJB 3756-99, 1999.

(編輯：楊 娟)

A method to estimate the balance calibration uncertainty

Liu Chunfeng, Xiong Lin*, Liu Jiahua, Li Haiyan

(China Academy of Aerospace Aerodynamic, Beijing 100074, China)

A complete uncertainty estimation process for balance calibration is established: assessing the calibration system uncertainty, assessing the bias limit and precision limit based on checking load residuals to estimate the uncertainty from other errors, and combining them to obtain the total uncertainty result. For the BCS-100 calibration system, balance TG624C is calibrated seven times repeatedly to implement the method. The result shows that: (1)The uncertainty caused by the roll angle of balance installation and the angular displacement of balance in the calibration are the main components, which shows the direction to upgrade the calibration system; (2)Due to the interference ofYandMz, the uncertainties ofQ、ZandMyare larger; (3) The precision limit is much smaller compared to the bias limit. The method is also applicable to other calibration systems.

uncertainty;calibration system;bias limit;precision limit;repeat

1672-9897(2016)02-0084-07

10.11729/syltlx20150109

2015-05-15;

2016-01-14

LiuCF,XiongL,LiuJH,etal.Amethodtoestimatethebalancecalibrationuncertainty.JournalofExperimentsinFluidMechanics, 2016, 30(2): 84-90. 劉春風, 熊 琳, 劉家驊, 等. 天平校準不確定度的一種評估方法. 實驗流體力學, 2016, 30(2): 84-90.

V211.752

A

劉春風(1988-)，男,河北承德人,工程師。研究方向：風洞天平。通信地址：北京市豐臺區云崗西路17號(100074)。E-mail：nuaa_lcf@126.com

*通信作者 E-mail: 17252081@qq.com