滿足故障可診斷性的傳感器配置方法

劉麗桑，胡曉強，彭俠夫*，萬斌浩

(1.福建工程學院信息科學與工程學院,福建福州350118;2.廈門大學航空航天學院,福建廈門 361005)

滿足故障可診斷性的傳感器配置方法

劉麗桑1，胡曉強2，彭俠夫2*，萬斌浩2

(1.福建工程學院信息科學與工程學院,福建福州350118;2.廈門大學航空航天學院,福建廈門 361005)

摘要：以系統的部件級物理結構或數學模型為對象,基于有向圖技術提出了非線性系統滿足故障可診斷性的傳感器優化配置方法．在對有向圖中故障檢測與分離概念進行定義的基礎上,設計了一種最小傳感器配置方法,討論了進一步優化的方法:1) 按照實際配置情況,以價格、質量、體積與功耗混合的最小代價原則替代最小數量原則,給出了以最小配置為出發點的優化搜尋算法;2) 考慮最小配置子集中某傳感器發生故障導致的故障可診斷性功能缺失,設計了一種后補償方法與一種直接補償的改進貪婪算法．并以衛星的動量輪系統為例進行仿真,仿真結果驗證了配置方法的有效性．

關鍵詞：傳感器配置;故障診斷;有向圖

在現代化的工業控制等領域中,故障診斷正受到越來越多的關注與重視．對系統實際過程行為測量的需要,決定了故障的可診斷性嚴重依賴于系統中配置的傳感器類型與數量．傳感器優化配置的研究始于20世紀70年代末,但相較于故障診斷領域,傳感器優化配置的研究還相當不充分,而且在理論上更不完善．

針對線性時不變動態系統,彭濤[1]提出了一種基于傳感器最優配置的混合H-/H∞故障檢測觀測設計方法,對建立的模型分別采用線性矩陣不等式(LMI)技術、Pareto遺傳算法等優化方法獲得系統設計的最優解．Rao等[2]從系統的實際物理結構中導出系統的有向圖,通過因果分析,將其轉化為故障與測點關系的二分圖,進而求出最小傳感器配置子集．劉睿等[3]以航天器部件為例對上述方法進行了工程上的實現．Commault等[4]基于線性系統的狀態空間描述,將系統故障與不確定擾動作為系統的輸入,討論了有向圖最大鏈路的規模與系統故障可診斷性的關系,將有向圖進行了等價分解與降維后實現了對傳感器的優化配置．戴文戰與陳杰等[5-6]使用故障傳遞矩陣,將故障傳播有向圖從二值定性分析量化為數值分析．Azam等[7]引入故障發生概率的概念,提出了一種基于優化問題的模型,通過有效的算法訓練,確定了對多故障組合診斷的傳感器配置．Rosich等[8]同樣基于優化問題的方法,以一種增量迭代算法,避免了Sarrat等[9]所使用的窮舉法中出現的計算復雜度隨候選傳感器數量的增加而呈現指數增長的缺點,同樣實現了最小成本的傳感器配置．文獻[10-12]對于線性或非線性微分代數方程,使用Dulmage-Mendelsohn分解技術,將系統的微分代數方程組分為3個部分:過約束部分、完全約束部分與欠約束部分．針對完全約束部分,通過提取測點之間的偏序關系,以最少傳感器數量實現了該部分故障可診斷配置．

本文使用有向圖方法,以跟蹤型貪婪算法求取滿足系統故障可診斷性的傳感器最小配置子集．以此為基礎,考慮質量、體積、功率等條件的約束,進一步分析了更符合實際情況的最小代價傳感器配置．針對所配置傳感器發生故障的情況,提出了冗余補償配置方法與一種直接補償的改進貪婪算法．最后,以動量輪系統為例,對方法的有效性進行了驗證．

1傳感器的初步優化配置

1.1基本概念

在使用有向圖進行滿足故障可診斷的傳感器配置問題中,我們將故障的可診斷性劃分為兩個層次:故障可檢測性與故障可分離性．現分別給出圖論中對故障可檢測與可分離的定義．

假設系統中共有k個既定故障,且在任意時刻最多只有一個既定故障發生．共有n個待選測點,組成集合S,其中選取了m個測點配置傳感器,組成的測點集合為Z,顯然有0≤m≤n,Z?S．

故障可檢測:當系統中某故障Fi發生時,其將對一系列的測點產生影響,將受其影響的測點集合記為Ai(Ai?S)．當且僅當Ai中至少有一個測點配置了傳感器時,即Ai∩Z≠?時,故障是可檢測的．

故障可分離：對于系統中存在的兩個不同作用位置的既定故障Fi與Fj,在分別滿足可檢測的基礎上,當兩者影響的測點集合的交集相對于其并集的補集中至少有一個測點配置了傳感器時,可保證兩個故障的系統輸出存在差異[2]．因此,可以在所有既定故障分別滿足了可檢測性的基礎上定義故障可分離性:故障Fi影響的測點集合為Ai,另一個故障Fj影響的測點集合為Aj,當兩個測點集合的交集相對于其并集的補集Bij中至少有一個測點配置了傳感器時,即存在關系式Bij∩Z≠?時,故障Fi與Fj可分離．若故障兩兩可分離,則系統故障是可分離的．

傳感器的配置問題可描述為如下形式:按一定的準則(如:個數最少或成本最低等)從測點候選集合S中選取若干個測點組成傳感器配置集合Z,以滿足上述故障可檢測性與可分離性要求．

1.2故障傳播有向圖的建立與簡化

故障傳播有向圖定性反映了系統的內部結構,同時亦反映了所研究的故障集合作用于系統的位置及其影響的傳播模式,是本文研究傳感器在滿足系統故障可診斷性的基礎上實現優化配置的基礎與出發點．

獲取故障傳播有向圖的方法有2種:

方法1:將系統的狀態空間描述或者微分方程組轉化為有向圖．以方程組中出現的變量以及微分變量作為節點建立故障傳播有向圖,對于微分方程右邊的每一個變量,其對應的節點都存在一條有向弧指向左邊微分變量對應的節點;由于微分變量影響相應的狀態變量,前者的節點也應存在一條指向后者節點的有向弧．若考慮如下非線性微分方程組：

(1)

其中，x1(t),x2(t),x3(t)為系統的狀態變量,w1(t),w2(t),w3(t)為系統的故障變量,各故障變量之間相互線性獨立地進入狀態方程．建立的故障傳播有向圖如圖1(a)所示．

方法2:直接通過系統的部件級結構圖獲取系統的有向圖．以每一個部件的輸出作為一個頂點,若一個輸出作為某部件的輸入對該部件的輸出具有影響,則在相應的頂點之間存在一條有向弧．該種方法直接從系統的實際結構出發,建立的有向圖的規模一般會大于第一種方法建立的有向圖模型,其在傳感器配置過程更加復雜的同時,亦增加了候選測點的選擇．

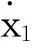
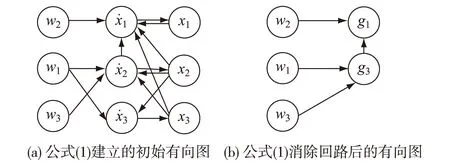
圖1　公式(1)所建立的故障傳播有向圖Fig.1The fault propagation digraph of formula

1.3最小傳感器配置

根據1.1節中的定義,在進行傳感器配置前,需確定每個故障的檢測點集合與兩兩故障間的分離集合,即對故障傳播有向圖進行因果分析．

所謂的故障因果分析,要求分別從每一個故障節點Fi出發,沿有向弧搜尋下一個頂點,將找到的頂點編號保存之后繼續搜尋;若遇到分叉口,保存其下標,沿一條路徑搜尋結束后返回分叉口繼續搜尋;當搜尋到只有入路沒有出路的頂點后,沿該方向的搜尋結束．最后將搜尋得到的該故障所能夠影響的所有測點組成故障的檢測集合:

Ai={Sj|若存在一條路徑從Fi到Sj}.

(2)

其中i=1,2,…，k,j=1,2,…，n．在確定了每一個故障的檢測集合之后,可以通過對比兩兩檢測集合的不同,得到故障分離集合

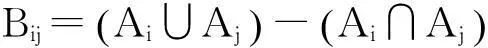
i,j=1,2,…，k且i≠j.

(3)

然后以故障檢測集合Ai與故障分離集合Bij為根節點,各測點為頂節點建立二分圖．若故障檢測集合Ai分離集合Bij中包含的某測點,則在相應集合與該測點之間存在一條有向弧指向該測點．

上述預處理結束后,使用跟蹤型貪婪算法[2]求取滿足故障可診斷性要求的最少數量傳感器配置方案:

1) 根據最大有效入度原則選取配置測點(所謂有效入度是指測點的實際入度減去其存貯的入度,表示了根節點可新增覆蓋的根節點數)．

2) 標記選擇測點所覆蓋的根節點,并從二分圖中刪除再次覆蓋的根節點與之前標記的測點之間的弧(即消去之前標記的測點可通過這次標記的測點實現對根節點的檢測與分離的功能)．

3) 存貯這次標記的根節點與未標記的測點之間的弧．

4) 判斷測點是否覆蓋了所有的根節點．是則轉5),否則返回1)．

5) 將具有實際入度的標記測點組成最小配置子集．

現以一個簡單的例子加以說明．考慮圖2所示的某故障傳播有向圖,為方便計算機的實現,將其故障二分圖表示為表1所示的鄰接矩陣形式．5個測點的有效入度分別為:8,9,8,5,8(該處使用從左到右規則),第1次配置測點選S2;第2次,有效入度分別為2,0,4,2,4,選S3為配置測點;未標記的3個測點的有效入度為0,1,1,隨意選取S4為配置測點,則二分圖的所有根節點得到標記,此時標記的3個測點的剩余入度分別為3,6,5．由上述方法可求得圖2所示系統的最小傳感器配置方案為Z={S2,S3,S4},且其配置方案不唯一,該配置可實現各個故障的檢測與R1,R2除外的各故障分離．

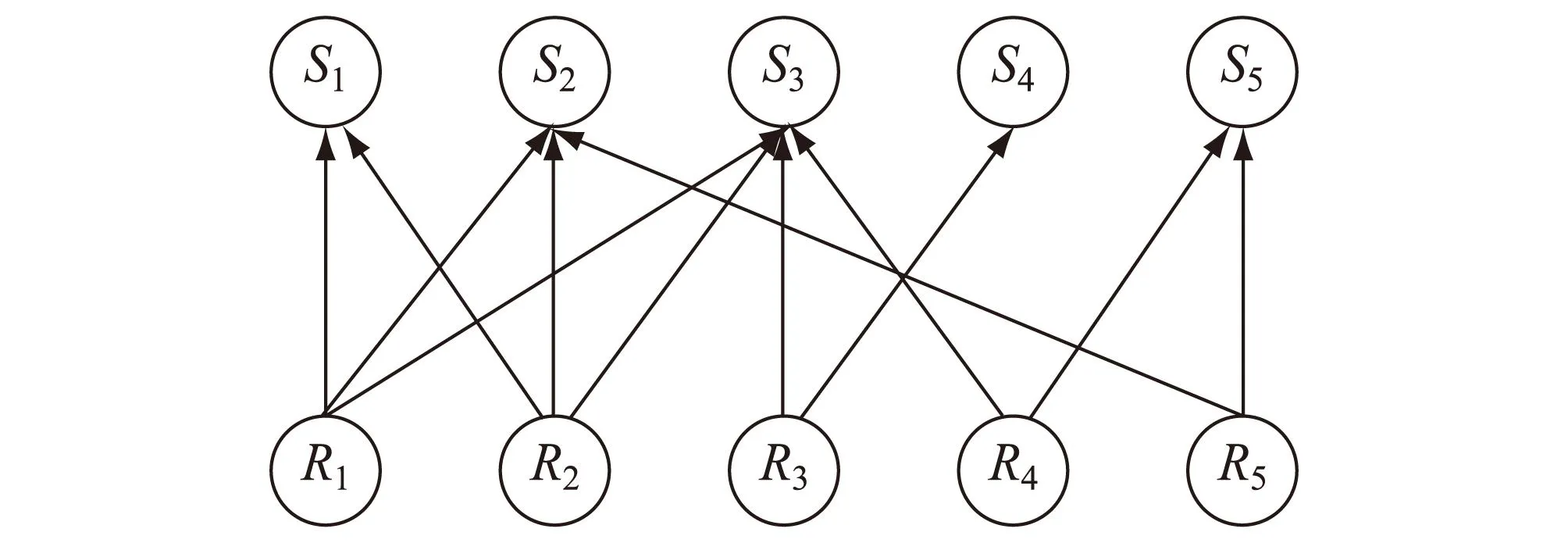
Ri為討論的系統故障；Si為系統的候選傳感器配置測點,i=1,2,3,4,5.圖2　某系統故障傳播有向圖Fig.2The fault propagation digraph of a system

2傳感器的進一步優化配置

2.1最小代價配置

在1.3節中,討論了使用跟蹤型貪婪算法求取系統最小傳感器配置集合的一般步驟．但在實際應用中,由于受到各種客觀條件的約束與限定,最小傳感器配置集合不一定是最優的,甚至并不一定是可行的．因此,需要在最小傳感器集合的基礎上,采用一種類似內點法的方法對配置問題進一步優化．所謂的內點法,是一種針對有約束非線性規劃問題的優化搜索方法．其中心思想是迭代序列從某個給定的內點(可行解)出發,不斷地逼近最優解．以傳感器配置的綜合代價為問題的目標函數,以配置滿足系統故障可診斷為約束條件,將最小代價配置描述為優化問題形式．

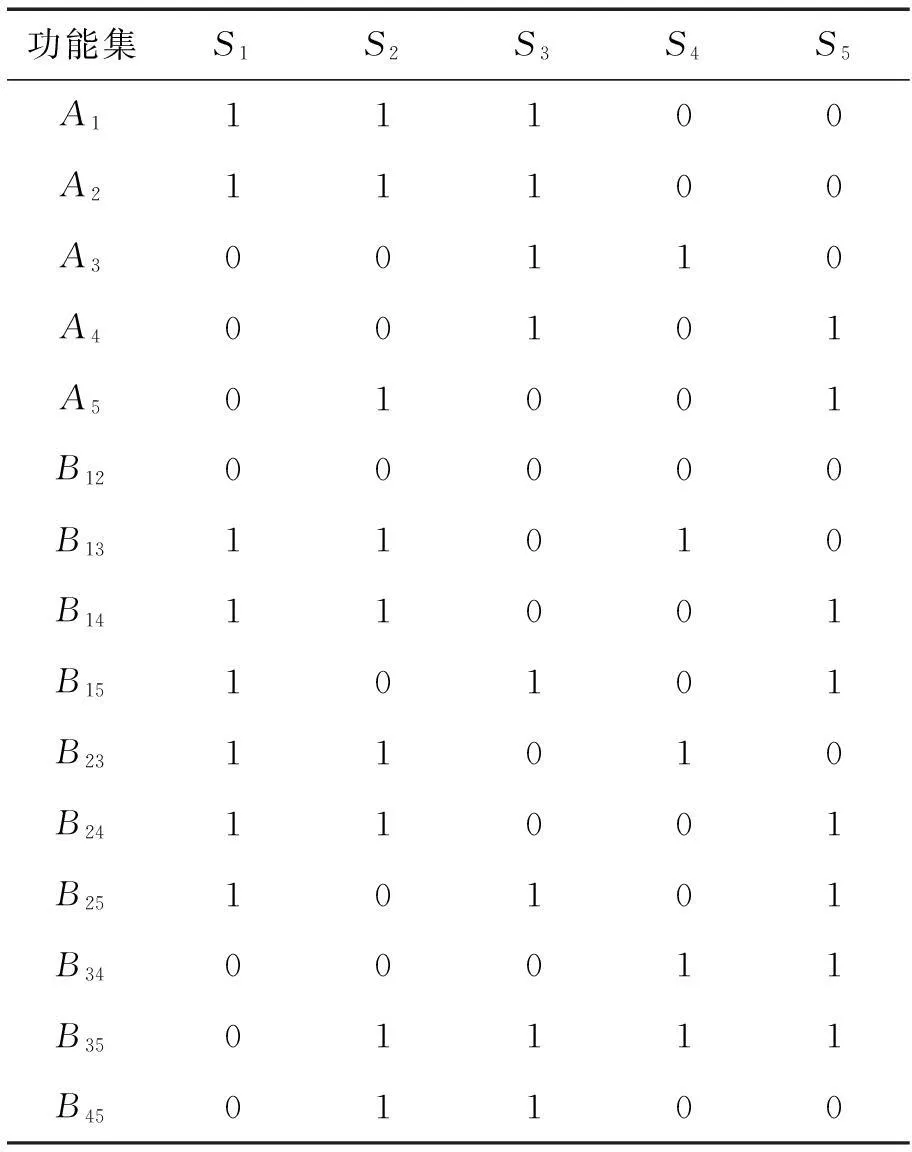
表1　圖2系統的故障二分圖

以列向量P,Q,V與E分別代表各個傳感器的價格、質量、體積、功耗，利用專家知識對各個指標的相對重要性進行評估,確定各指標的權重,形成權重列向量L．最后以二值列向量C表示傳感器的配置情況,其中

則目標函數可表示為如下形式:

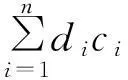
(4)

其中di為第i個測點的綜合代價,di=l1pi+l2qi+l3vi+l4ei,n為候選測點個數．而對于系統必須配置的測點,人為將其代價置為0;對于某指標超出系統設計范疇的傳感器,將其代價置為充分大．

觀察目標函數的表達形式,可以將S值視為n維賦范空間內某點的車比雪夫范數．對于二維空間,車比雪夫范數意義下的等值線為d1c1+d2c2,對于三維空間,車比雪夫范數意義下的等值面為d1c1+d2c2+d3c3．則對于n個候選測點,S的數值應位于對應的n維空間上的某一等值超平面上．

設計搜尋算法為：

1) 以最小傳感器配置子集(m個傳感器)總代價所在的等值超平面為出發點,選擇兩兩傳感器配置代價之差的最大公約數作為搜尋步長h,向原點方向收縮等值超平面至代價最小的m個傳感器的代價總和P2．

2) 在每一個超平面以內搜尋接近于超平面且使系統滿足故障可診斷性的測點子集．如若找到這種測點子集,則其在總代價原則下優于最小配置子集．

2.2有向圖的降維

最小代價配置程序大量使用遞歸調用,這使得程序對大數據的處理不僅需要一個較大的堆棧對現場進行保護,而且需要耗費大量的時間．因此,在預處理階段通過某些方法人為的降低問題的規模就顯得十分有必要．基于對二分圖鄰接矩陣的分析,可以實現在一定程度上對問題進行降維．

1) 對比二分圖鄰接矩陣的每一行,合并對于測點的影響完全相同的兩行．

2) 對比二分圖鄰接矩陣的每一列,找出對于檢測集與分離集響應完全相同的測點,將它們合記為一個測點．

3) 搜尋二分圖鄰接矩陣的每一行,找出入度為1的根節點,則對應的測點即為必須配置傳感器的基本測點,所有的基本測點組成基本測點集,剩余測點組成剩余測點子集．

4) 將與基本測點集中任意測點相關聯的每一個根節點刪除,記剩余根節點組成的集合為Y．

配置問題即可化為:從剩余子集中按某一原則選取配置子集,以完全覆蓋剩余根節點集Y．

圖2所示的系統二分圖經過降維后的二分圖鄰接矩陣如表2所示,其實質上是將故障1與故障2合并為一個故障．

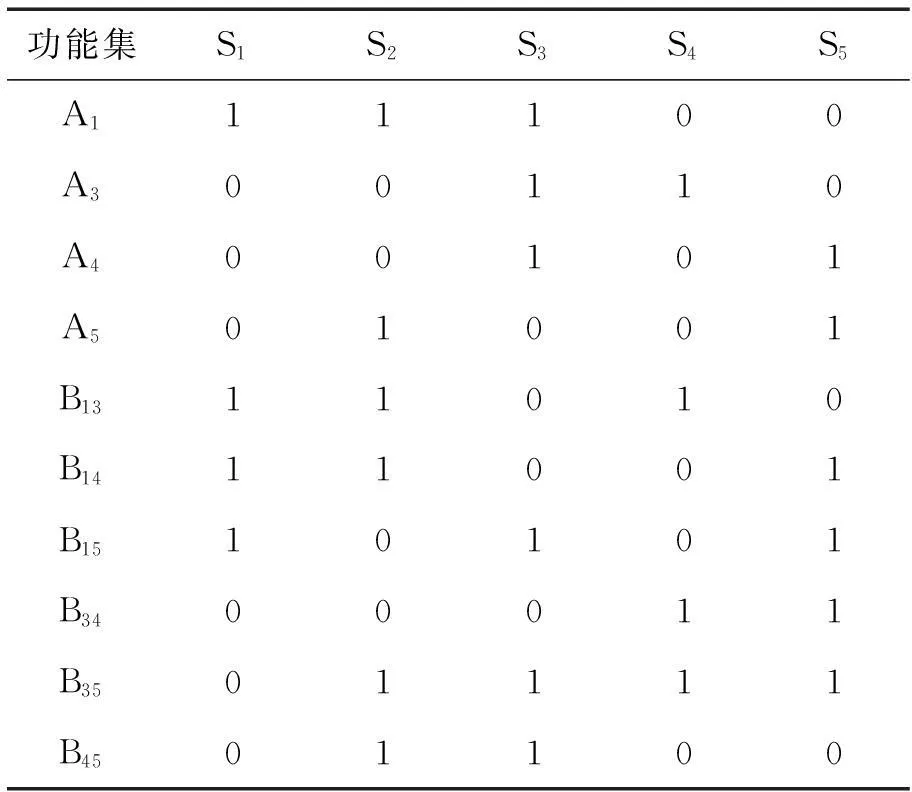
表2　圖2系統的降維故障二分圖

2.3傳感器故障補償配置

對于一個系統,其傳感器可分為2種類型：第1種是為了實現反饋控制所配置的傳感器,這種傳感器是系統正常運行的重要組成部分,可通過上述故障傳播有向圖,將其作為系統的一部分進行討論；第2種是為了實現系統故障診斷所配置的傳感器,這種傳感器的故障,雖然并不會直接影響系統的正常運行,但卻嚴重影響了系統故障的檢測與分離．當系統某一故障發生時,可能由于相關傳感器的故障而無法對發生的故障進行診斷,使該故障長期潛伏于系統之中．對于這種傳感器的故障,可以通過冗余配置,消除其影響．下文在最小傳感器配置的基礎上對該種傳感器的故障補償問題進行研究．

假設某傳感器故障的輸出值恒定不變,將不能反映系統的故障發生，那么由于該傳感器故障,在故障二分圖中對應測點所覆蓋的根節點就有可能重新暴露出來．傳感器故障補償配置的核心是確定暴露出的檢測或分離功能并將其重新覆蓋．所以設計傳感器故障補償配置的步驟如下：

1) 對最小配置集合中的每一個傳感器,在假設其故障的基礎上,分析配置集合對于系統各故障的輸出響應,確定損失功能．若某故障的響應為0,則系統失去了對該故障的檢測能力與分離該故障與其他故障的分離能力;若不同故障的響應相同,則系統失去了分離這2種故障的能力．

2) 將各傳感器故障所損失的診斷功能(Ai,Bij)定義為補償集合G,并以G中的元素為根節點,測點為頂節點,構造補償配置的二分圖．

3) 使用跟蹤型貪婪算法,求解出最小補償配置集合．

考慮表2所示的降維系統，其某一最小配置方案為Z1={S2,S3,S4}．分別假設3個測點的傳感器發生故障,則失去的診斷功能為M1={A4,A5,B14,B15,B34,B35,B45},需要的補償配置為{S3,S5}．而對于另一種配置方案Z2={S2,S3,S5},M2={A3,B13,B34,B35},需要的補償配置為{S4}．

由上述討論可以看出,不同的傳感器最小配置方案,在其傳感器發生故障的情況下，損失的故障診斷功能數量相差巨大,所需要的補償配置也因此不盡相同．分析配置測點與故障診斷功能之間的關系,列于表3,可以發現,傳感器發生故障損失的故障診斷功能都是在現有配置方案下只實現了一次覆蓋的功能項以及與損失的檢測項相關的分離項．

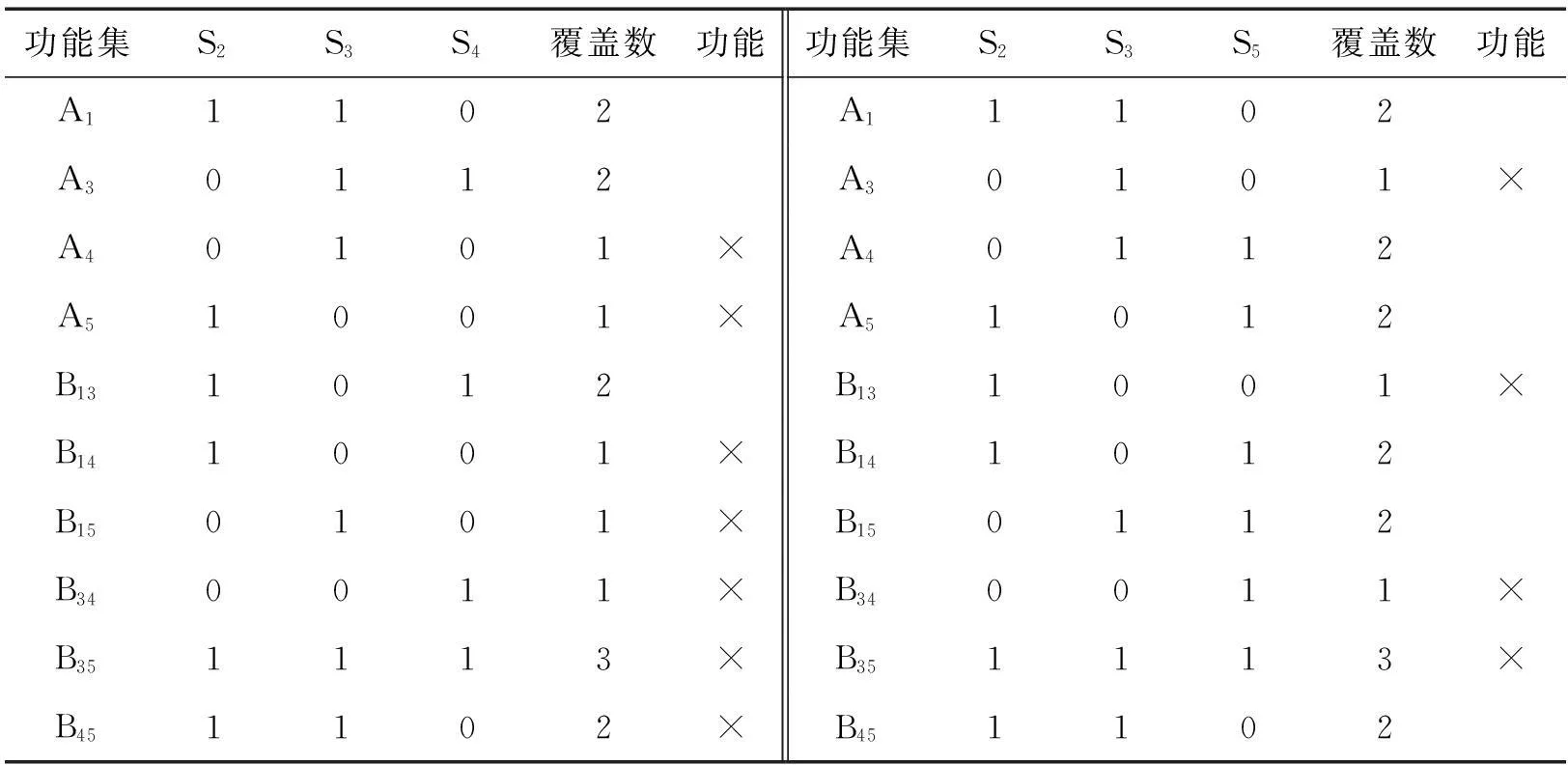
表3　配置測點與診斷功能二分圖

注：表中的×表示該檢測或分離功能喪失;空白表示功能仍然可以實現.

現給出一種改進的貪婪算法,其中心思想是在第1次進行傳感器配置時即保證故障診斷功能的2次覆蓋,則當任意某一配置傳感器故障時,亦可保證整個系統診斷功能的完整性．其過程如下:

1) 根據最大有效入度原則(實際入度與存貯入度之差)選取配置測點,若有多個測點有效入度最大,則優先選擇未標記測點．

2) 標記選擇測點與其所覆蓋的所有根節點.

3) 若某根節點為第2次標記,存貯該根節點與未標記的測點之間的弧,并將其從待定根節點集合中刪除．

4) 若某根節點多于2次標記,從二分圖中刪除該根節點與之前標記的測點之間的弧．

5) 判斷待定根節點集合是否為空．是則轉6),否則返回1)．

6) 將具有實際入度的標記測點組成最小配置子集．

考慮表2所示的降維系統．5個測點的有效入度分別為:4,6,6,4,6,隨意選取(該處使用從右到左的規則)S5為配置測點;第2次選擇時,5個測點的有效入度仍為:4,6,6,4,6,但依據未標記者優先,選擇S3為配置測點;第3次,各測點有效入度為:3,4,3,3,3,易見選S2為配置測點;第4次時,有效入度分別為:1,1,1,3,1,選取S4;最后,驗證選取的4個測點的剩余實際入度分別為:5,5,4,5．所以使用改進貪婪算法的配置結果為Z={S2,S3,S4,S5}．

3應用舉例

考慮如圖3所示的衛星動量輪系統[3],經回路處理后的故障傳播有向圖如圖4所示,其中S為可配置傳感器的測點,F為故障源,測點與S8必須配置傳感器．僅考慮系統相互獨立的較大部分,并隨機假設各測點傳感器價格分別為250,300,350,300,350,150,350,400,200,200,150,300,300與350元．

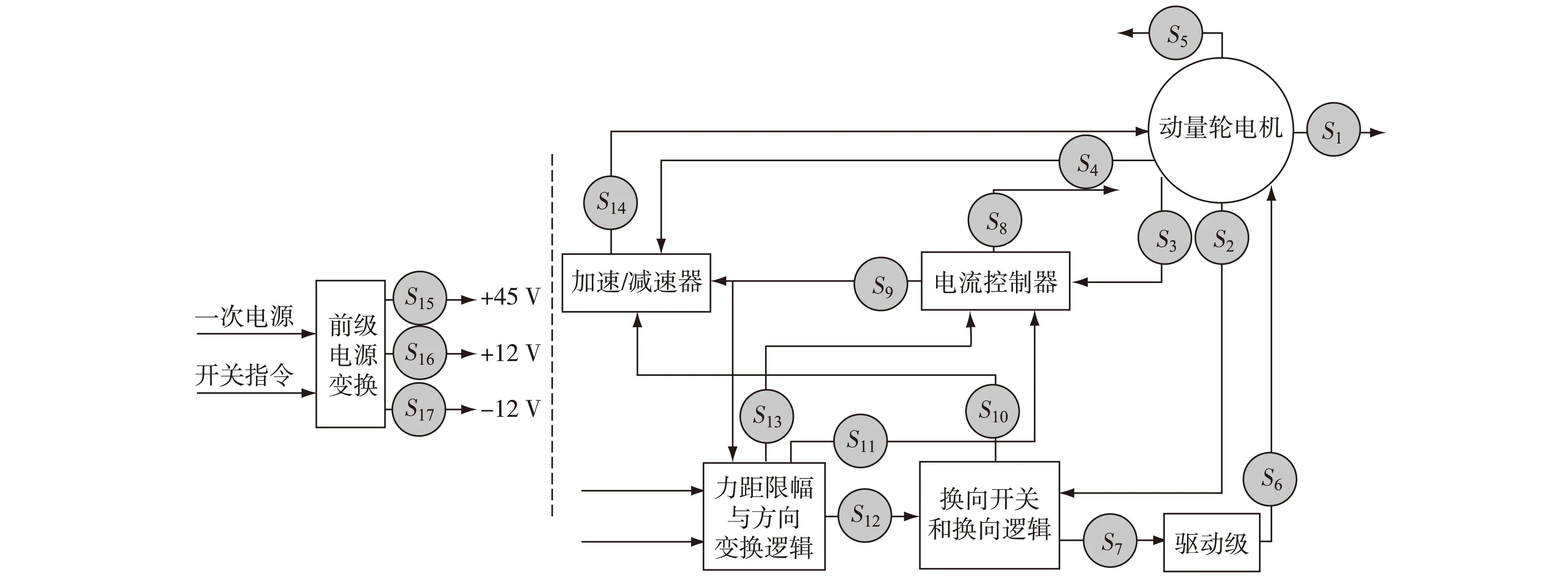
圖3　動量輪系統測點示意圖Fig.3The selected points graph of the momentum wheel system

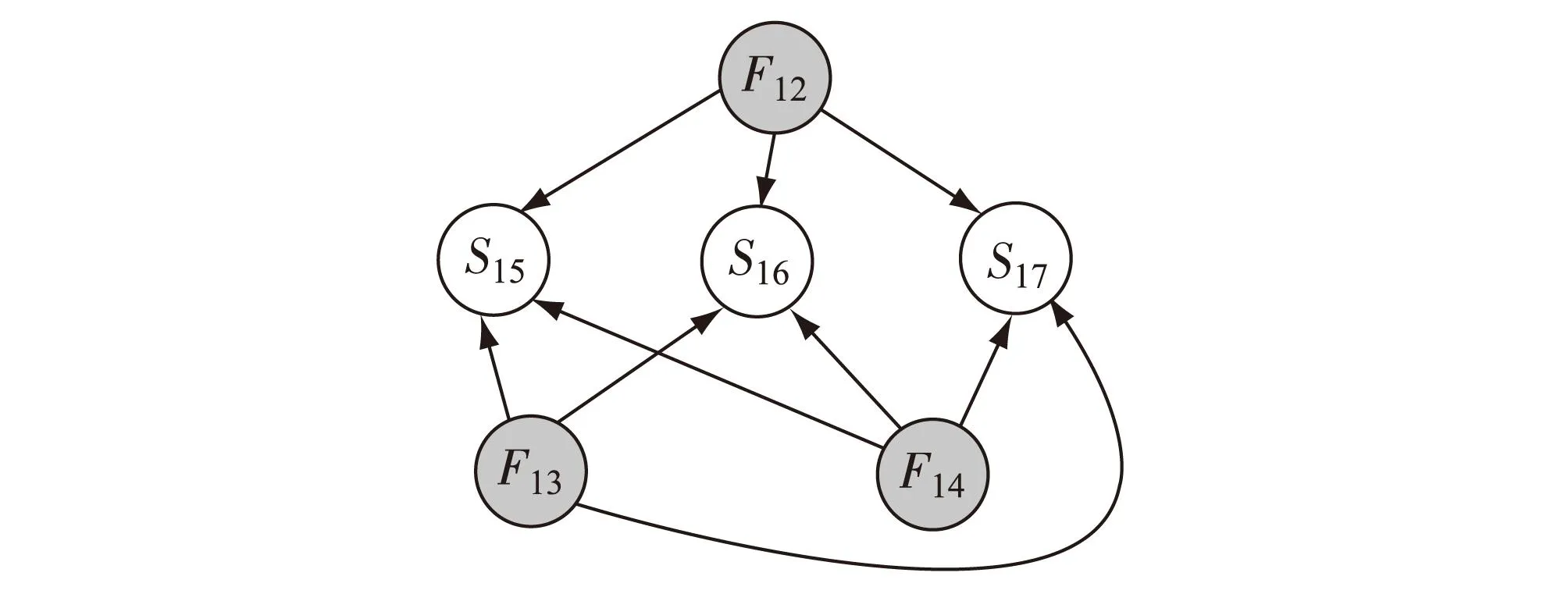
圖4　動量輪系統的故障傳播有向圖Fig.4The fault propagation digraph of the momentum wheel system

對圖4進行因果分析，可以看出F1與F2，F9,F10與F11所影響的測點集合完全相同，所以它們是不可分離的故障，為方便表示，將F1與F2合記為Ff，將F9,F10,F11合記為Fs.使用1.3的貪婪算法求取最小傳感器配置方案，如表4所示，經過7次迭代，根據有效入度最大原則先后標記了S9,S10,S1,S8,S7,S12與S13后，二分圖的根節點得到了完全的覆蓋.但在刪減之后的二分圖中，S9的剩余實際入度已經變為0，這說明對于最小傳感器配置集合，測點S9是

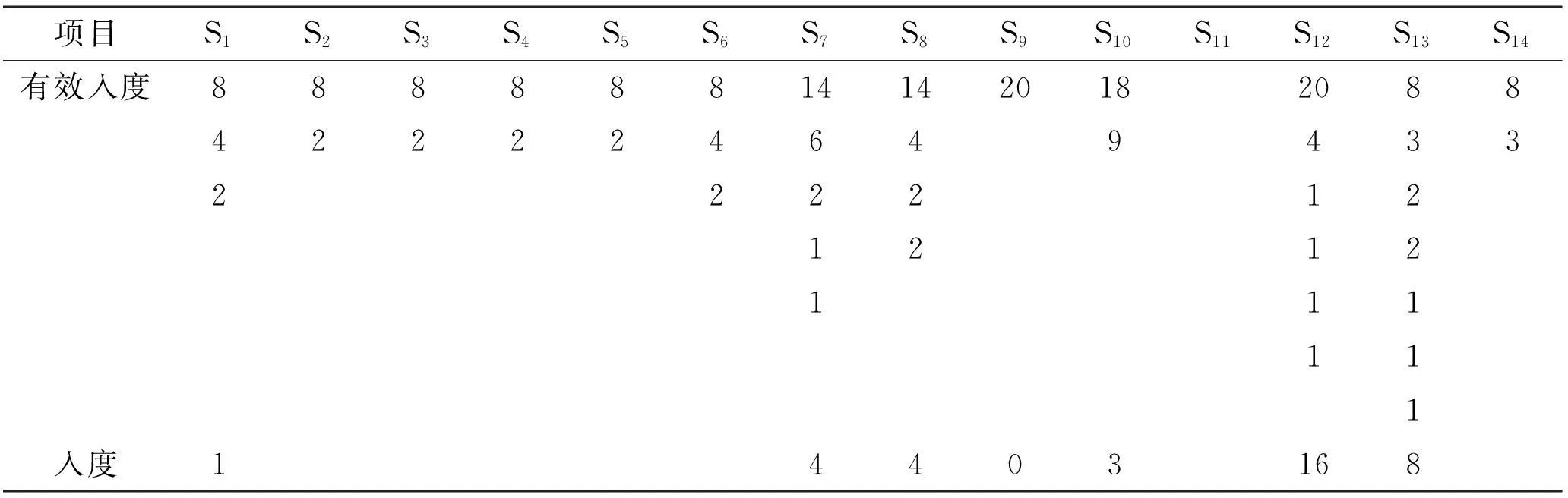
表4　動量輪系統迭代過程

一個冗余配置，其檢測故障與分離故障的功能可以通過其他配置的測點加以實現，應將其從最小配置集合中除去.所以該動量輪系統滿足故障可診斷的最小傳感器配置為：{S1,S7,S8,S10,S12,S13}.

本文只考慮傳感器的價格指標．根據文獻[5],軸承溫度遙測測點S5與電流控制器電流遙測測點S8在動量輪中是必須設置傳感器的測點．因此本文在討論最小代價配置問題時,人為的將上述兩個測點所配置的傳感器價格置為0．

根據表4,最小配置集合{S1,S7,S8,S10,S12,S13}包含6個傳感器,其總成本為250+350+0+200+300+300=1 400,隨機選取6個傳感器的最小成本為800 (S11并沒有用處)．記候選測點的總數為n=14-1-2=11,最少配置測點數為6,以傳感器價格兩兩之差的最大公約數為步長，即h=50．搜尋得到的集合{S6,S7,S10,S12,S13},總價格相對最小配置少了100,為1 300,且滿足了兩個特定測點必須配置傳感器的要求．

綜上所述,{S5,S6,S7,S8,S10,S12,S13}為最小代價配置,實際總代價為1 850元．而由于系統存在大量必須配置傳感器的基本測點,最小傳感器配置的補償配置達到極差情況,為{S1,S7,S8,S10,S12,S13}．

4結論

本文對于滿足故障可診斷性的傳感器優化配置問題,從系統的物理結構和數學模型出發,采用了有向圖的定性方法．在不考慮個別部件的非線性特性的情況下,分析了故障的傳播模式,以最小傳感器配置方法為基礎,給出了最小代價傳感器配置方案與傳感器故障補償方案．但上述問題沒有考慮系統不確定性對傳感器優化配置的影響,還有待今后進一步的研究．

參考文獻：

[1]彭濤．基于傳感器最優配置的故障檢測方法研究[D]．長沙:中南大學,2005:15-70.

[2]RAOR,MANIB,RAGHUNATHANR．Locatingsensorsincomplexchemicalplantsbasedonfaultdiagnosticobservabilitycriteria[J]．AicheJournal,1999,45(2):310-322.

[3]劉睿,周軍,李鑫，等．基于DG的航天器部件可診斷性測點配置方法[J]．系統工程與電子技術,2014,36(10):2013-2017.

[4]COMMAULTC,DIONJM．Sensorlocationfordiagnosisinlinearstructuredsystemswithdisturbances[C]∥Proceedingsofthe42ndIEEEConferenceonDecisionandControl．Maui,USA:IEEE,2004:1443-1448.

[5]戴文戰,陳杰．一種故障傳播模型及故障源分離算法[J]．廈門大學學報(自然科學版),2001,40(S1):63-67.

[6]陳杰,戴文戰．基于故障傳遞概率的故障源位置診斷方法[J]．廈門大學學報(自然科學版),2001，40(S1):58-62.

[7]AZAMM,PATTIPATIK,PATTERSON-HINEA．Optimalsensorallocationforfaultdetectionandisolation[C]∥Systems,ManandCybernetics,2004IEEEInternationalConferenceonIEEE.Hague,Netherland:IEEE,2004:1309-1314.

[8]ROSICHA,SARRATER,PUIGV,etal．Efficientoptimalsensorplacementformodel-basedFDIusinganincrementalalgorithm[C]∥Proceedingofthe46thIEEEConferenceonDecisionandControl．LosAngeles，USA:IEEE,2007:2590-2595.

[9]SARRATER,PUIGV,ESCOBETT,etal．Optimalsensorplacementformodel-basedfaultdetectionandisolation[C]∥Proceedingofthe46thIEEEConferenceonDecisionandControl.LosAngeles,USA:IEEE,2007:2584-2589.

[10]KRYSANDERM,ASLUNDJ,NYBERGM．Anefficientalgorithmforfindingminimaloverconstrainedsubsystemsformodel-baseddiagnosis[J]．IEEETransactionsonSystemsManandCyberneticsPartA:SystemsandHumans,2008,38(1):197-206.

[11]KRYSANDERM,FRISKE．Sensorplacementforfaultdiagnosis[J]．IEEETransactionsonSystemsManandCyberneticsPartA:SystemsandHumans,2008,38(6):1398-1410.

[12]劉文靜,劉成瑞,王南華．基于可診斷性約束的測點優化配置研究[J]．空間控制技術與應用,2011,37(2):1-5.

Methods of Sensor Placement for Fault Diagnosis

LIU Lisang1,HU Xiaoqiang2,PENG Xiafu2*,WAN Binhao2

(1.College of Information Science and Engineering,Fujian University of Technology,Fuzhou 350118,China;2．School of Aerospace Engineering,Xiamen University,Xiamen 361005,China)

Abstract:Based on the directed graphs (DG),this paper investigates the method for optimizing the sensor configuration which can meet the fault diagnosability of nonlinear system described by component-level physical structure or a mathematical model．On one hand,a greedy algorithm satisfied failure detectability and separability is introduced particularly．Some discussions of the optimization method are made from two directions then．With the minimum configuration generated by the greedy algorithm as a starting point,a further searching algorithm in the principle of minimum cost which is considered as the hybrid of price,weight,volume and wastage makes the configuration of system sensors to be more realistic．On the other hand,in consideration of losses of failure diagnostic capability leaded by faulted sensor in minimum sensor configuration,this paper presents a compensated sensor configuration to all potential lost fault diagnostic functions and improves the greedy algorithm to achieve a direct compensation．Finally,the proposed approach is validated by using the momentum wheel system as an example.

Key words:sensor configuration;fault diagnostic;directed graph

doi：10.6043/j.issn.0438-0479.2016.03.022

收稿日期：2015-10-20錄用日期：2016-02-18

基金項目：國家自然科學基金(61305117,61374037);國家重點實驗室開放基金(9140c59030411ht05)

*通信作者：xfpeng@xmu.edu.cn

中圖分類號:TP 274.5

文獻標志碼：A

文章編號：0438-0479(2016)03-0434-07

引文格式：劉麗桑，胡曉強，彭俠夫，等.滿足故障可診斷性的傳感器配置方法.廈門大學學報(自然科學版)，2016,55(3)：434-440.

Citation：LIU L S,HU X Q,PENG X F,et al．Methods of sensor placement for fault diagnosis.Journal of Xiamen University(Natural Science)，2016,55(3)：434-440．(in Chinese)