增廣拉格朗日子集模擬優化方法

董喬月，李洪雙

(南京航空航天大學 航空宇航學院，南京　210016)

增廣拉格朗日子集模擬優化方法

董喬月，李洪雙

(南京航空航天大學 航空宇航學院，南京210016)

摘要：傳統的工程結構優化設計方法在求解多設計變量、多約束條件的結構優化設計問題時，存在諸多不足，針對上述問題，基于增廣拉格朗日約束處理方法和子集模擬優化方法發展一種新的結構優化設計方法——增廣拉格朗日子集模擬優化方法(ALSSO)。該方法首先利用拉格朗日乘子法處理多重約束條件，然后利用子集模擬優化方法對轉化后的無約束優化問題進行求解；對罰函數因子的更新方法進行改進，以保證收斂過程的穩定性；利用兩個算例對該方法的計算精度、穩健性以及計算效率進行驗證，并與其他優化方法進行對比。結果表明：增廣拉格朗日子集模擬優化方法具有非常優秀的尋優性能。

關鍵詞：結構優化設計；子集模擬優化方法；拉格朗日乘子法；罰函數因子

0引言

結構優化設計問題在工程結構設計中較為常見，20世紀40年代以前，多采用圖解法、數學求極值和經典力學分析法研究簡單結構的最小質量設計問題；20世紀50年代后，隨著數學建模和計算機技術的完善，對工程系統進行自動優化設計技術得到迅速發展和應用。計算機能在給定條件下得到最優設計方案，縮短設計周期，提高設計質量[1]。

工程結構優化問題通常是在多重約束條件下使所設計結構的重量最輕或者費用最低，約束條件是指對結構的應力、位移、屈曲等力學響應量的限制。而在實際應用中，求解有約束優化問題是非常困難的，其原因是：①設計變量的數量多，②可行域的高度不規律，③約束條件的數量多。因此，人們不斷尋求、探索既能在復雜設計區域中進行最優解的搜索，又可處理多重約束條件的優化方法。

目前，工程上所用的優化方法大致可分為兩類：一類是基于梯度的數值優化方法，另一類是基于自然現象的啟發而發展的隨機型優化方法。隨著工程結構優化問題越來越復雜，采用基于梯度的數值優化方法進行求解后的優化結果的可信度也在逐漸減小，其原因是當求解優化問題遇到上文所提的三個問題時，數值優化方法得出的優化結果通常不是全局最優的，甚至可能是不可行的。而隨機型優化方法在處理上文所提的三個問題時，能夠彌補數值優化方法的缺點和不足，因此受到了高度關注。雖然目前已有較多的隨機型優化方法且在結構優化設計領域被廣泛應用，例如遺傳算法[2]、粒子群優化算法[3]、模擬退火算法[4]、蟻群優化算法[5]、和聲搜索算法[6]等，但仍沒有一種優化方法可以求解所有的結構優化設計問題，尋找更加高效、穩健的隨機型優化方法是未來努力的方向。

本文基于子集模擬優化方法，結合拉格朗日乘子法，發展一種用于求解有約束優化問題的增廣拉格朗日子集模擬優化方法，采用兩個典型算例驗證所發展方法的尋優能力、穩健性以及計算效率，并與其他優化設計方法進行對比。

1子集模擬優化方法原理

子集模擬(Subset Simulation)是一種高效的蒙特卡羅策略，最初被用于求解高維小失效概率結構可靠性問題[7]，后期研究表明，子集模擬也是一種隨機型優化方法[8-9]。其基本思想是：一個極值事件(優化問題)可以看作是一個稀有事件(可靠性問題)的特例，二者之間的轉換關系如圖1所示。

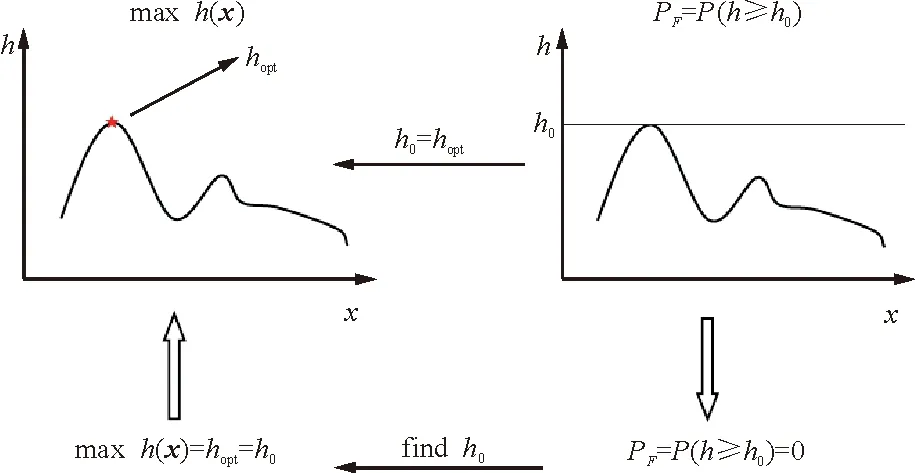
圖1　優化問題與可靠性問題之間的轉換

考慮如下無約束全局優化問題：

maxh(x)x∈S

(1)

式中：h(x)為目標函數；x∈S為設計變量集合；S為問題定義域。

為了在可靠性問題的框架內研究優化問題，人為地令設計變量x為隨機變量并且指定(用戶定義)概率分布類型，因此所得到的目標函數也是隨機變量，并且具有其自身的概率密度函數與累積分布函數。上述將確定性的變量“拓展”為隨機變量的概念是利用蒙特卡羅策略解決復雜問題的一種計算方法。設定hopt是h的全局最大值，此時有x=xopt。累積分布函數的性質決定了累計分布函數曲線必定是右連續且單調不減的。可靠性問題中所尋找的“失效概率”PF定義為

PF=P(F)=P[h(x)≥hopt]

(2)

式中：失效事件F=[h(x)≥hopt]。

顯然，失效概率等于0，因為hopt為全局最大值。在優化問題中，并不關注該失效概率，而是重點研究目標函數達到最大值的點或區域。

子集模擬方法的思想為：在式(2)中，P[h(x)≥hopt]可以表示為一系列條件概率的乘積。條件概率{pi:i=1,2,…}用于定義中間失效事件，中間失效事件相應的分界值{hi:i=1,2,…}由式(3)估計給出。

(3)

式中：Fi為由模擬過程中的目標函數值所確定的中間事件。

根據乘法定理有：

(4)

在子集模擬優化中，改進的Metropolis-Hasting(MMH)算法[7]用于生成條件樣本，并逐漸靠近目標函數的最大值。這相當于把可靠性問題中的稀有事件區域逐漸發掘出來。對于擁有至少一個全局最大值的優化問題，可以將尋找hi→hopt的過程看作是尋找PF→0的過程。在優化過程中，子集模擬算法生成一系列中間目標函數的值{hi:i=1,2,…}，它們最終趨向全局優化點hopt。同時，樣本分布逐漸從概率密度函數(用戶指定)定義的寬廣區域，變為包含全局優化方案xopt在內的狹小區域。

子集模擬優化方法的運行過程如下：

(1) 選擇輸入變量的分布參數。在確定性優化算法中，每一個輸入設計變量都是確定性參數，但是在子集模擬優化算法中，輸入設計變量是隨機的，并且有一個假設的概率密度函數(PDF)fi(xj)。

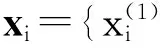
(3)MMH算法用于生成中間事件中的條件樣本。在第k層迭代中，從Fk-1中每個“種子”樣本開始生成一條馬爾可夫鏈。由于初始樣本服從條件分布，所有馬爾可夫鏈都是平穩的，并且每條馬爾可夫鏈上的樣本都滿足條件分布。每條馬爾可夫鏈的長度為1/pk-1(k=2,…)，其中pk-1為上一層迭代的條件概率。為新生成的樣本目標函數值進行計算與排序，從序列里確定第N(1-pk)個樣本和相應的目標函數值，這些篩選出的樣本為下一層迭代提供了“種子”樣本。

(4) 重復上述步驟直到滿足收斂條件或者達到最大可負擔計算量。

(5) 關于無約束子集模擬優化方法的描述和討論，詳見參考文獻[8]。

2增廣拉格朗日子集模擬優化方法

2.1增廣拉格朗日約束處理方法

拉格朗日乘子法將約束條件加入目標函數中，形成拉格朗日函數：

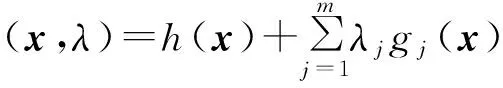
(5)

式中：λj為第j個約束的拉格朗日乘子；gj(x)為約束條件。

類似于罰函數方法，式(5)將有約束優化問題轉變為無約束優化問題。拉格朗日函數可以作為無約束目標函數使用，原因是有約束優化問題的最優解同樣適用于該無約束優化問題。但因為該解不一定是拉格朗日函數的最優解，所以為了保證該解的可行性與最優性，在增廣拉格朗日函數中加入一個增廣函數θ[10]，則整個函數為

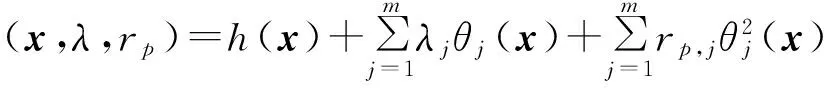
(6)

(7)

式中：h(x)為第i個樣本的目標函數值；ei(x)為等式約束違反值；gj(x)為不等式約束違反值；-λj/2rp,j從基于梯度的優化問題中選擇得到[11]。

增廣拉格朗日乘子法不同于標準的拉格朗日乘子法，因為多了罰函數一項；其也不同于標準的罰函數法，因為多項式里包括了拉格朗日乘子。在增廣拉格朗日函數里，每個約束的可行性將使用一個單獨的罰函數因子rp來判定。因為每個約束條件的罰函數因子是一個有限值，所以得出的結果必定是一個局部最優解[10]。最優點處的拉格朗日乘子和罰函數因子是未知的，且根據問題的不同而不同。每一層迭代過程中，拉格朗日乘子和罰函數因子都保持固定。每一層迭代之后，拉格朗日乘子根據該層優化結果進行如下更新[10]：

(8)

在迭代過程中，通過增大罰函數因子來阻止結果向不可行性方向發展，當約束值低于約束違反限定值εg時，罰函數因子便會減小[10]：

(9)

式中：ψj(xk)為等式或者不等式約束的約束違反值。

ψj(xk)的定義為

(10)

式中：ei(x)為等式約束的約束違反值；gj(x)為不等式約束的約束違反值。

罰函數因子的下限值為

(11)

2.2增廣拉格朗日子集模擬方法的基本框架

增廣拉格朗日子集模擬優化方法由兩部分組成：外部循環用來構成增廣拉格朗日函數，更新拉格朗日乘子和罰函數因子，并且檢驗優化過程是否收斂；在內部循環中，子集模擬優化算法求解無約束全局最優問題，即拉格朗日乘子和罰函數因子在內部循環中均保持固定值。增廣拉格朗日子集模擬優化方法的流程圖如圖2所示。

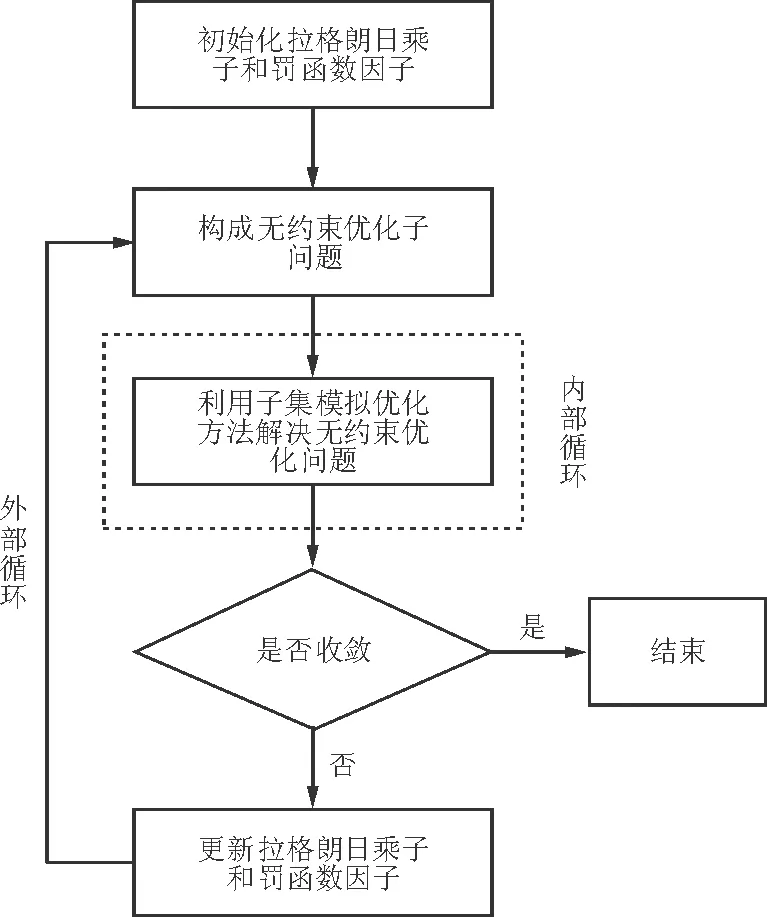
圖2　增廣拉格朗日子集模擬優化方法流程圖

內部循環中所使用的子集模擬優化方法在解決高維設計變量優化問題上具有優勢，而本文發展的增廣拉格朗日約束處理方法能夠很好地處理多約束條件。增廣拉格朗日子集模擬優化方法在處理多設計變量、多約束、復雜可行域的優化問題上表現出非常優秀的性能，將在第3節中通過多設計變量、多約束算例對此進行驗證。

2.3初始化與迭代

最優解x*不能僅通過求解一個無約束優化問題而得到，這是因為拉格朗日乘子和罰函數因子的值是未知的，并且根據問題的不同而不同。因此，需要對拉格朗日乘子和罰函數因子設定初始值，在后續的迭代過程中，還應對二者進行更新，根據文獻[10，12-13]，將拉格朗日乘子的初始值設定為0。

罰函數因子的初始值假設為一個單位矩陣，即r0=[1,…,1]T。K.Sedlaczek等[10]提出了一個更新罰函數因子的方法，即式(9)，但是該方法經常會造成罰函數因子的值在每層迭代時都產生數值上的變化，從而導致拉格朗日乘子在收斂過程中不穩定并且增加了計算量。

本文采用如下更新公式：

(12)

式中：φi(x*k)為計算約束違反值函數，對于等式約束，φi(x*k)=ei(x*k)，對于不等式約束，φi(x*k)=|gi(x*k)|。

與原始更新方法不同，改進后的更新方法只有在前一層迭代沒有使得優化結果變好的情況下才會增加罰函數因子的值，當最優解x*k是一個可行解時，罰函數因子將保持一個確定值。

為了保證拉格朗日乘子更新的有效性，為所有罰函數因子值設定一個下限值：

(13)

在最初的迭代過程中，由于罰函數因子太小而不能得到有效的最優解，該下限值具有重要作用。

2.4收斂準則

收斂準則是對于外部循環而言的，經過增廣拉格朗日方法處理過的優化問題的最初收斂準則為：如果λk-1和λk差的絕對值小于或等于給定的容限值ε，則可以判定優化過程已經收斂。但由于收斂過程中的不穩定性，改進后的優化方法使用另外一個收斂準則來保證優化結果的可行性。假設x*k是第k層迭代后得到的全局最優解，程序終止時，最優解滿足：

ρ(x*k)≤ε

(14)

式中：ρ(x*k)為可行性標準。

ρ(x*k)的定義為

(15)

拉格朗日子集模擬優化方法在大多數情況下能夠給出很好的優化結果，但在某些情況下，如果程序運行到最大迭代次數后仍未滿足收斂準則，則最后一次迭代的最優解也可被看作是該優化問題的近似解。

3算例驗證

將增廣拉格朗日子集模擬優化方法用于求解桁架結構優化設計和機翼翼盒結構優化問題，并與其他著名優化算法進行對比。

桁架結構優化問題計算單層所用樣本數為100、200和500，機翼翼盒結構優化問題單層所用樣本數為100。所用條件概率p均為0.1。內部循環的子集模擬優化最大迭代次數選擇為20，外部循環的最大迭代次數選擇為50。子集模擬優化以及所有的約束容限都設定為ε=10-4。在桁架結構優化算例中，算例被運行30次來驗證所發展優化算法的統計學性能，包括最好優化解、最差優化解以及平均優化解，并驗證所發展算法的穩健性。

3.172桿空間桁架結構優化

72桿空間桁架結構如圖3所示，桁架桿件材料的彈性模量為10 000ksi，材料密度為0.1lb/in3。

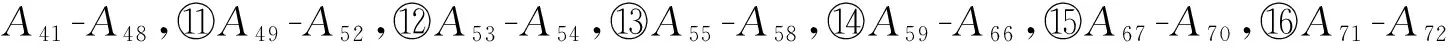
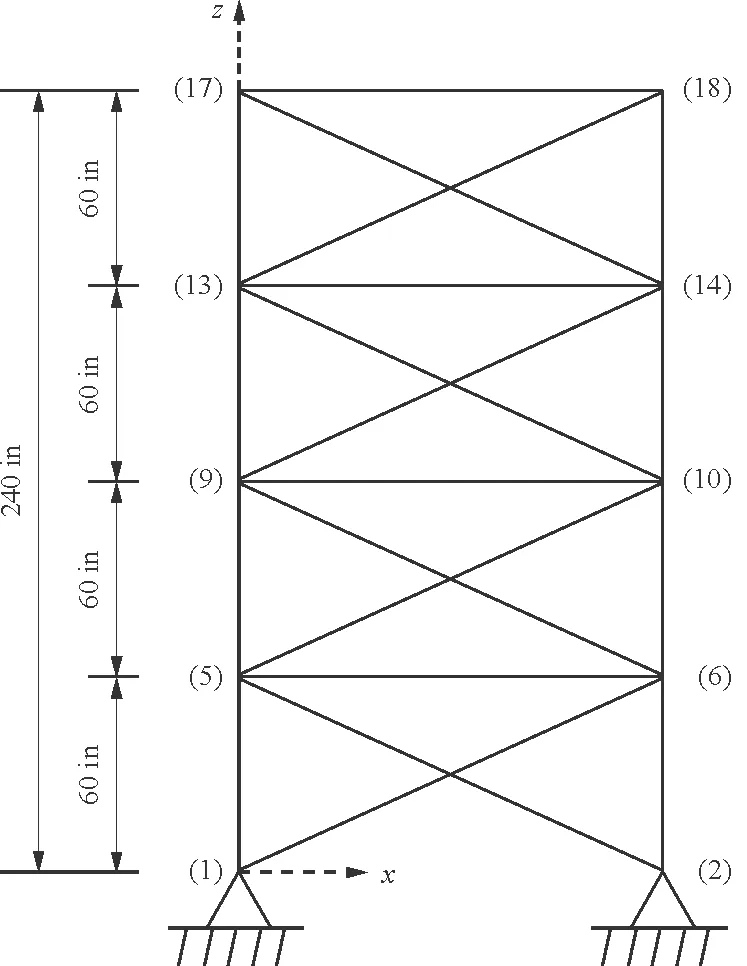
(a) 側視圖

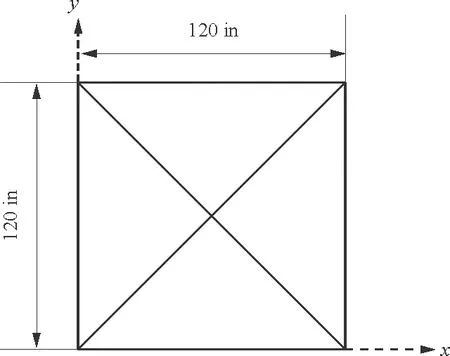
(b) 俯視圖

(c) 斜視圖

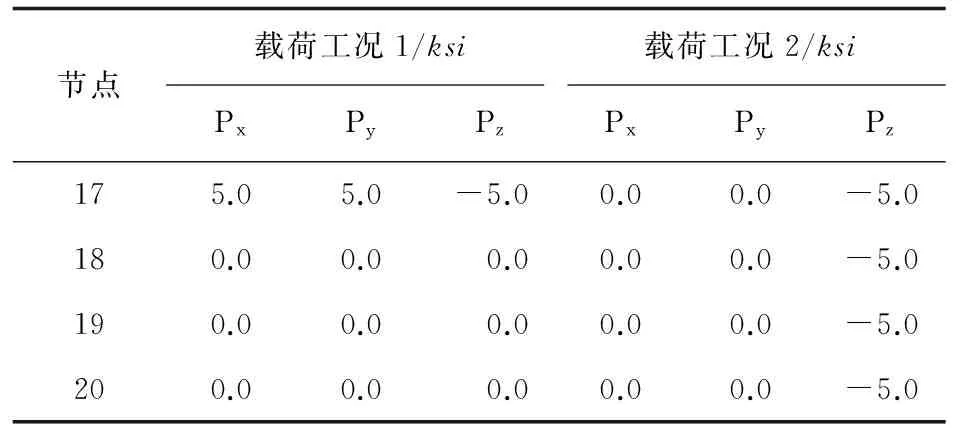
節點載荷工況1/ksi載荷工況2/ksiPxPyPzPxPyPz175.05.0-5.00.00.0-5.0180.00.0 0.00.00.0-5.0190.00.0 0.00.00.0-5.0200.00.0 0.00.00.0-5.0

72桿空間桁架結構優化問題已被遺傳算法(GA)、蟻群優化算法(ACO)[14]、和聲搜索算法(HS)[6]、粒子群優化算法(PSO)[15]及增廣拉格朗日粒子群優化算法(ALPSO)[12]等多種優化算法求解過。增廣拉格朗日子集模擬優化方法(ALSSO)的優化結果與上述優化算法優化結果的對比如表 2所示，表中同時給出了最優設計變量值、最小重量的優化結果、最大應力和最大位移的值。

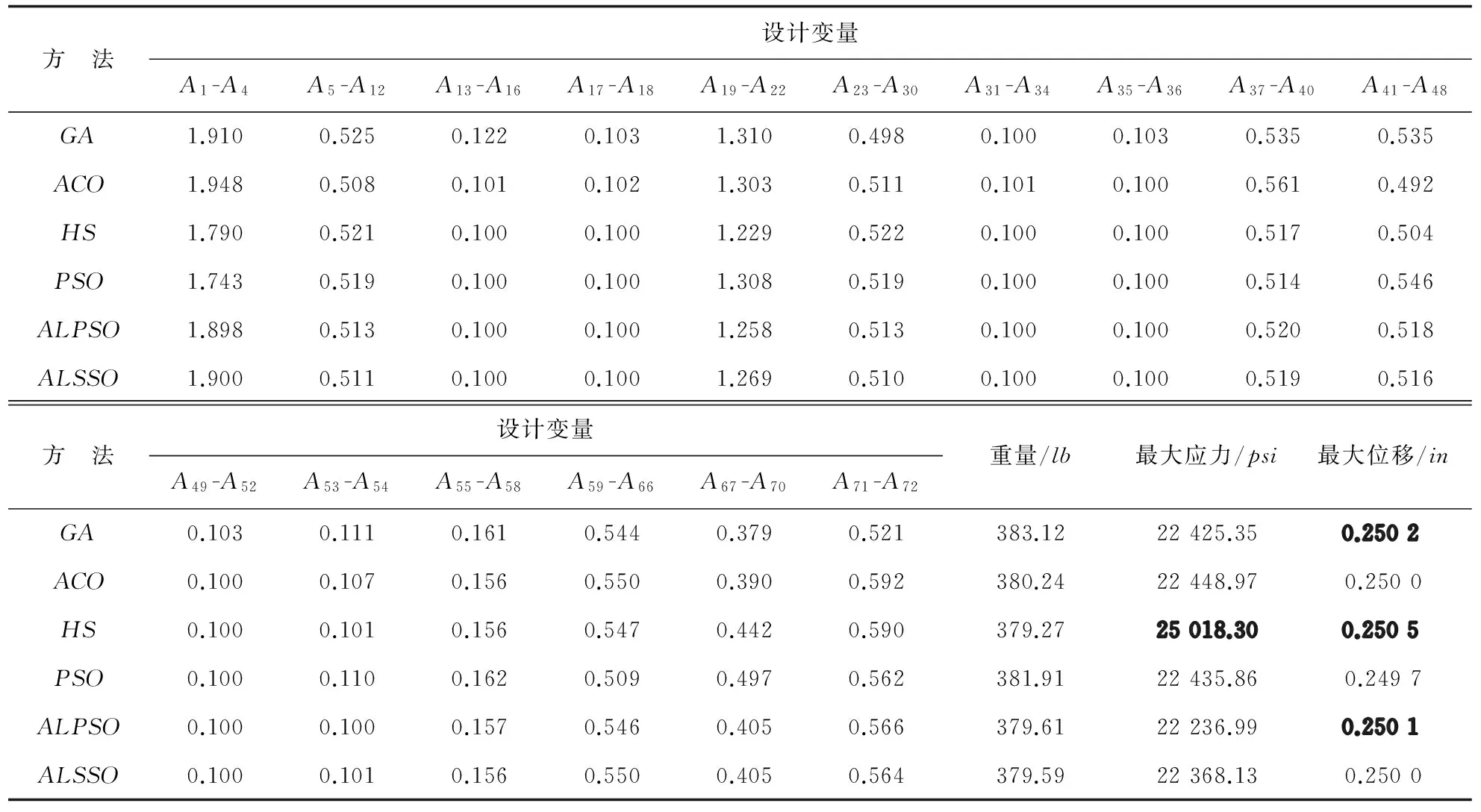
表2　72桿空間桁架結構優化結果對比

從表2可以看出：遺傳算法、和聲搜索算法、增廣拉格朗日粒子群優化算法的優化結果均違反了位移約束條件，同時，和聲搜索算法還違反了最大應力約束條件，故采用上述三種優化算法求解所得的最優解均為不可行解；在所有具有可行解的優化結果中，增廣拉格朗日子集模擬優化方法的最終優化結果(379.59lb)優于蟻群優化算法的最終優化結果(380.24lb)和粒子群優化算法的最終優化結果(381.91lb)，表明增廣拉格朗日子集模擬優化方法具有很好的尋優準確性。

隨著優化迭代次數的增加，結構重量的優化過程如圖4所示，優化過程所用單層樣本數為500。

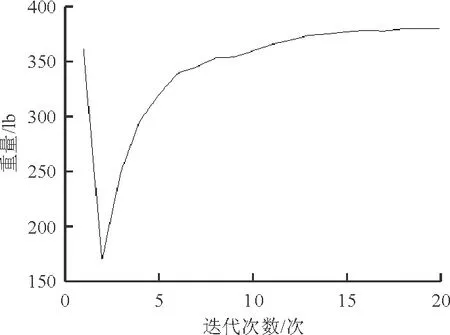
圖4　72桿空間桁架結構迭代過程

從圖4可以看出：在72桿空間桁架結構優化問題中，增廣拉格朗日子集模擬優化方法在第17次迭代時便已收斂，得出的最優重量值為379.59lb，表明增廣拉格朗日子集模擬優化方法的計算效率高、收斂快。

在72桿空間桁架結構優化問題中，增廣拉格朗日子集模擬優化方法的統計學性能如表3所示，表中變異系數(COV)一列用來反映優化方法的穩健性。所有結果都是在30次獨立運算后取得，所用單層樣本數量分別為100、200和500。

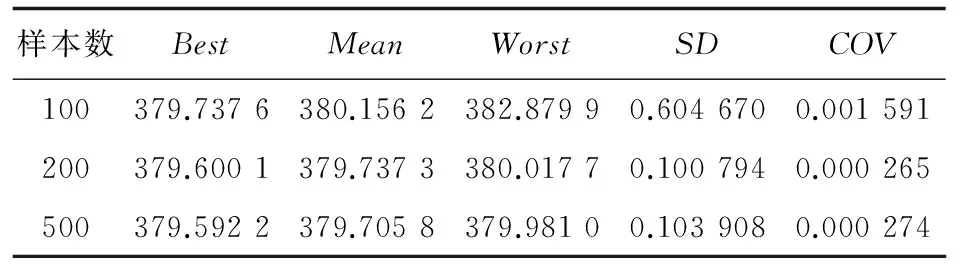
表3　72桿空間桁架結構統計學性能

從表3可以看出：三種樣本量的變異系數值均很小，表明增廣拉格朗日子集模擬優化方法具有很好的穩健性。

3.2機翼翼盒結構優化設計

機翼翼盒結構如圖5所示，該結構關于x -y平面(結構中心面)對稱。

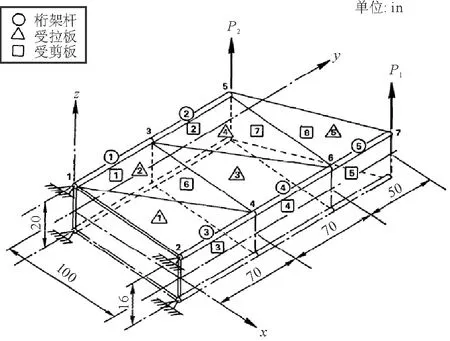
圖5　機翼翼盒結構

選取機翼翼盒結構的上半部分作結構說明，在該結構的優化問題中，對于桿件單元，取桿件的橫截面積為設計變量，橫截面積的下限為0.1in2、上限為2.0in2。對于平面板，取板的厚度為設計變量，平面板分為受拉板(CST)和受剪板(SSP)，受拉板單元由矩形區域1243、矩形區域3465以及三角形單元567構成，其中兩個矩形區域可分別看作由兩個三角形受拉板構成，三個區域的受拉板厚度分別獨立，受拉板厚度的下限為0.02in、上限為1.00in；受剪板厚度的下限為0.02in、上限為1.00in。機翼翼盒結構的節點坐標、桁架桿單元的編號與設計變量分組、受拉板單元的編號與設計變量分組以及受剪板單元的編號與設計變量分組參見參考文獻[16]。整個機翼翼盒結構共16個設計變量，分別為5個桿件的橫截面積，3個受拉板的厚度以及8個受剪板的厚度。在節點1和節點2處三個方向的位移邊界條件為0。桁架桿、受拉板和受剪板所用材料相同，材料許用應力為10 000lb/in2，彈性模量為107lb/in2，密度為0.02lb/in3，泊松比為0.3。結構有兩種載荷工況，分別為：在節點7處受沿z軸正向，大小為5 000lb的集中力；在節點5處受沿z軸正向，大小為10 000lb的集中力。機翼翼盒結構所受位移約束為各節點在z方向上的位移均不得超過2in，所受應力約束為各單元的許用應力是10 000lb/in2。

在Abaqus中通過參數化建模建立機翼翼盒結構的有限元模型。受拉板和受剪板采用S4R殼單元建立，桁架采用T3D2桿單元建立。整個模型結構通過共節點裝配得到，邊界條件設定為左邊界四節點鉸支。載荷工況設定為：在分析步1中設定模型結構受工況1中載荷作用，并在分析步2中取消工況1中的載荷作用；在分析步2中設定模型結構受工況2中的載荷作用。為了保證結構在兩種工況下均達到最優設計，分別取分析步1與分析步2中的應力與位移分析結果，并設定兩個分析步所得結果的最大值作為該優化問題的應力與位移約束結果。

利用增廣拉格朗日子集模擬優化方法對該機翼翼盒結構進行優化設計，并與其他優化方法相比較，優化結果如表4所示，表中包括最優設計變量值和最小重量。ACCESS1優化方法[16]為NASA報告中提出的一種基于梯度的優化算法，Gallatly&Berke方法和Gallatly方法為R.A.Gallatly等[17-18]提出的優化算法。上述三種優化方法均為基于梯度的優化方法，并且所得出的最優解均滿足結構所要求的位移及應力約束條件。

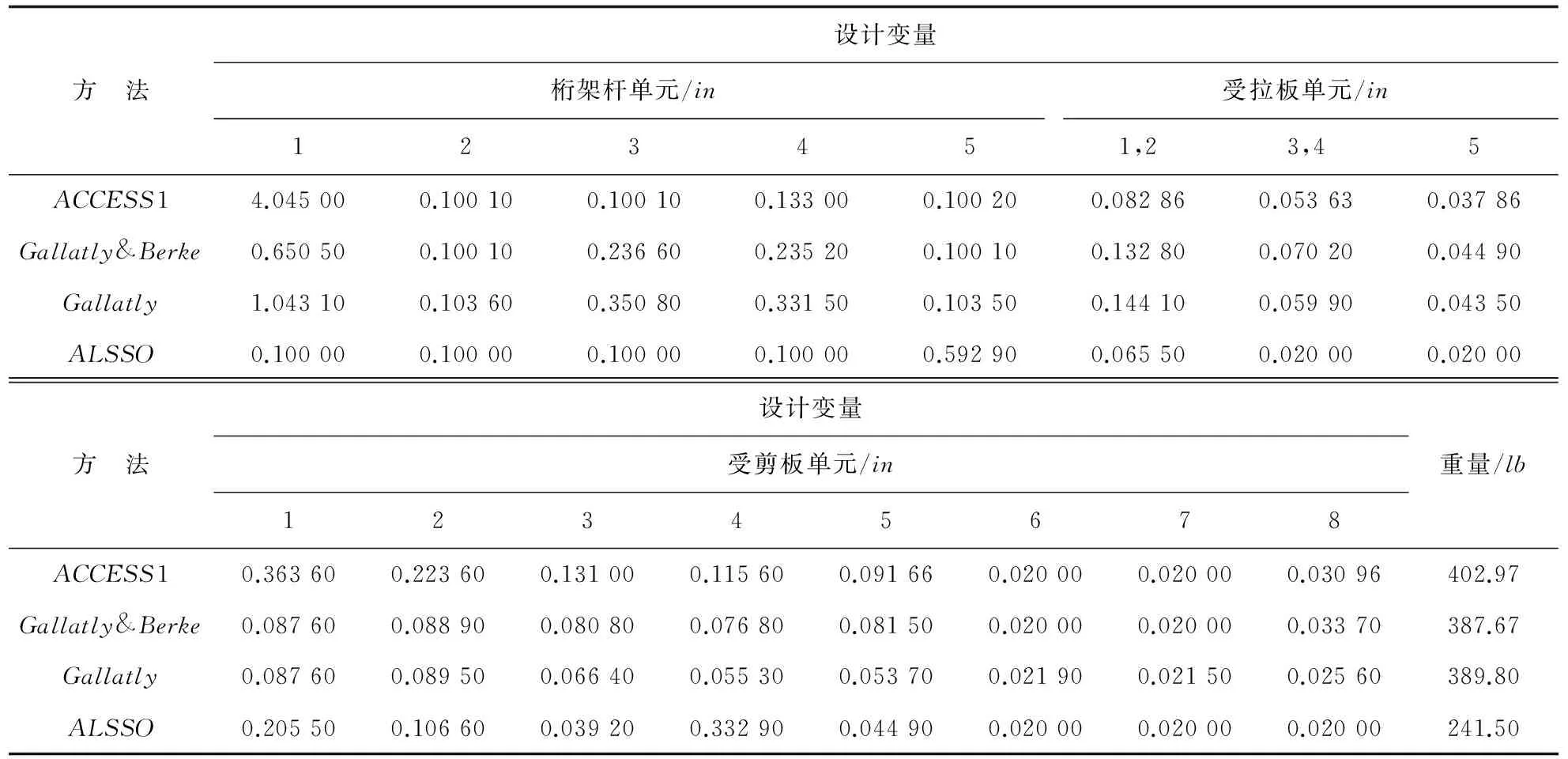
表4　機翼翼盒結構優化結果

從表4可以看出：增廣拉格朗日子集模擬優化方法得出的最優設計明顯優于其他方法所得的最優設計，表明增廣拉格朗日子集模擬優化方法具有優秀的尋優能力。

機翼翼盒結構優化設計迭代過程如圖6所示，所用單層樣本數為100。

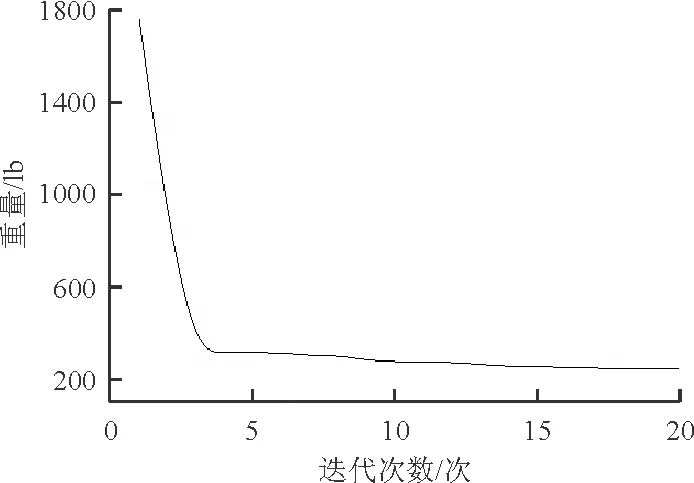
圖6　機翼翼盒結構優化迭代過程

從圖 6可以看出：在第15次循時該翼盒結構優化過程達到收斂，表明增廣拉格朗日子集模擬優化方法具有較高的計算效率。

4結論

本文將拉格朗日乘子法與子集模擬優化方法結合起來，發展了一種可用于結構優化設計的增廣拉格朗日子集模擬優化方法，并利用兩個工程算例對該方法的尋優能力和穩健性進行了驗證。增廣拉格朗日子集模擬優化方法是對原始子集模擬優化方法的改進與拓展，在求解多設計變量、多約束條件的結構優化設計問題上，具有更為優異的性能。

參考文獻

[1] 李為吉， 宋筆鋒， 孫俠生， 等. 飛行器結構優化設計[M]. 北京： 國防工業出版社， 2005.

LiWeiji,SongBifeng,SunXiasheng,etal.Aircraftstructureoptimization[M].Beijing:NationalDefenseIndustryPress, 2005.(inChinese)

[2]AdeliH,KumarS.Distributedgeneticalgorithmforstructuraloptimization[J].JournalofAerospaceEngineering, 1995, 8(3): 156-163.

[3]LiLJ,HuangZB,LiuF.Aheuristicparticleswarmoptimizationmethodfortrussstructureswithdiscretevariables[J].Computers&Structures, 2009, 87(7/8): 435-443.

[4]LambertiL.Anefficientsimulatedannealingalgorithmfordesignoptimizationoftrussstructures[J].Computers&Structures, 2008, 86(19/20): 1936-1953.

[5]KavehA,TalatahariS.Aparticleswarmantcolonyoptimizationfortrussstructureswithdiscretevariables[J].JournalofConstructionalSteelResearch, 2009, 65(8/9): 1558-1568.

[6]LeeKS,GeemZW.Anewstructuraloptimizationmethodbasedontheharmonysearchalgorithm[J].Computers&Structures, 2004, 82(9/10): 781-798.

[7]AuSK,BeckJL.Estimationofsmallfailureprobabilitiesinhighdimensionsbysubsetsimulation[J].ProbabilisticEngineeringMechanics, 2001, 16(4): 263-277.

[8]LiHS,AuSK.Designoptimizationusingsubsetsimulationalgorithm[J].StructuralSafety, 2010, 32(6): 384-392.

[9]LiHS.Subsetsimulationforunconstrainedglobaloptimization[J].AppliedMathematicalModelling, 2011, 35(10): 5108-5120.

[10]SedlaczekK,PeterR.UsingaugmentedLagrangianparticleswarmoptimizationforconstrainedproblemsinengineering[J].StructuralandMultidisciplinaryOptimization, 2006, 32(4): 277-286.

[11]RockafellarRT.ThemultipliermethodofHestenesandPowellappliedtoconvexprogramming[J].JournalofOptimizationTheory&Applications, 1973, 12(6): 555-562.

[12]JansenPW,PerezRE.ConstrainedstructuraldesignoptimizationviaaparallelaugmentedLagrangianparticleswarmoptimizationapproach[J].Computers&Structures, 2011, 89(13/14): 1352-1366.

[13]LongW,LiangXM,HuangYF,etal.AhybriddifferentialevolutionaugmentedLagrangianmethodforconstrainednumericalandengineeringoptimization[J].Computer-AidedDesign, 2013, 45(12): 1562-1574.

[14]CampCV,BichonBJ.Designofspacetrussesusingantcolonyoptimization[J].JournalofStructuralEngineering, 2004, 130(5): 741-751.

[15]PerezRE,BehdinanK.Particleswarmapproachforstructuraldesignoptimization[J].Computers&Structures, 2007, 85(19/20): 1579-1588.

[16]SchmitLA,MiuraH.Approximationconceptsforefficientstructuralsynthesis[J].AIAAJournal, 1976, 14(12): 692-699.

[17]GellatlyRA,BerkeL.Optimalstructuraldesign[R].FlightDynamicsLaboratory, 1971.

[18]GellatlyRA.Developmentofproceduresforlargescaleautomatedminimumweightstructuraldesign[R].FlightDynamicsLaboratory, 1966.

Augmented Lagrangian Subset Simulation Optimization Method

Dong Qiaoyue, Li Hongshuang

(College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:In solving the structural optimization problems with multiple design variables and multiple constraints, traditional optimization design method of engineering structure has many disadvantages. A new structural optimization method, which is based on subset simulation optimization(SSO) and the Lagrangian multiplier method, is developed to solve structural optimization problems under constraints. The Lagrangian multiplier method is used to handle multiple constraints. Then, SSO is used to solve the transformed unconstrained problem and search for the global optimum. In order to guarantee the robustness of convergence, the updating method of penalty factor is modified for this purpose. The accuracy, robustness and efficiency of the proposed method are demonstrated by two examples. The optimization results of proposed method are compared with those obtained by other optimization methods available in the literature. It indicates that the proposed method has excellent performance on searching for the global optimum.

Key words:structural optimization design; subset simulation optimization; Lagrangian multiplier method; penalty factor

收稿日期：2016-03-01；修回日期：2016-04-01

基金項目：國家自然科學基金(U1533109,11102084)

通信作者：李洪雙,hongshuangli@nuaa.edu.cn

文章編號:1674-8190(2016)02-165-09

中圖分類號：V214.19

文獻標識碼：A

DOI：10.16615/j.cnki.1674-8190.2016.02.005

作者簡介：

董喬月(1991-)，男，碩士研究生。主要研究方向：飛行器結構設計、飛行器結構優化設計。

李洪雙(1978-)，男，博士，副教授。主要研究方向：飛行器可靠性工程、飛行器結構優化設計。

(編輯：馬文靜)

江蘇高校優勢學科建設工程資助項目