數控機床溫度敏感點變動性及其影響

苗恩銘　劉　義　高增漢　劉　輝

合肥工業大學，合肥，230009

數控機床溫度敏感點變動性及其影響

苗恩銘劉義高增漢劉輝

合肥工業大學，合肥，230009

摘要：數控機床熱誤差補償技術中的核心問題是建立能夠反映機床溫升與熱誤差之間的數學模型，其精度和穩健性則取決于模型自變量能否準確地反映機床溫度場分布特性，即溫度敏感點選擇結果是否準確和穩定。通過對Leaderway-V450型數控加工中心主軸Z向的多批次空轉數據進行分析發現，溫度敏感點存在變動性特征，導致自變量間多重共線性程度發生變化，進而對模型的預測精度和穩健性產生嚴重影響。由于主成分回歸算法具有消除自變量共線性影響作用，故提出采用該算法進行建模，并通過實際機床進行實踐檢驗。結果表明，采用主成分回歸算法建模，顯著降低了溫度敏感點變動性對模型預測精度的影響，能保證模型具有很好的預測精度和穩健性。

關鍵詞：數控機床；溫度敏感點；多重共線性；主成分回歸

0引言

在數控機床加工過程中，機床各部件不均衡溫升引起的熱誤差使得刀具和工件之間的相對正確位置發生了變化，從而造成零件的加工誤差。據統計，數控機床熱誤差約占總誤差的50%～70%[1-2]。通過應用設計和制造技術改進床身結構的硬件補償方法，不僅成本高，而且效果并不十分理想。因此，對數控機床熱誤差軟件補償技術進行研究具有重要意義[3]。

在數控機床軟件熱誤差補償技術中，核心問題是建立預測精度高、穩健性強的數學模型[4]。目前國際上通常是在數控機床上布置大量的溫度傳感器，通過建立傳感器溫度變量與機床熱誤差的函數關系來建立數控機床熱誤差補償模型[5]。這就要求溫度傳感器的安放位置既能最大限度地反映溫度場的分布特性，又能保證各傳感器之間具有較低的共線性干擾以實現模型的穩健性預測，這些位置稱之為溫度敏感點[6]。近年來，科研人員對溫度敏感點的選擇進行了大量研究。Attia等[7]采用有限元方法分析機床整體溫度場，并將溫度場劃分為多個比較規則的單元，通過溫度場仿真和相關性選擇，預測溫度測點的最優數量和最佳分布。Lo等[8-9]對溫度傳感器進行分組搜索、尋優，利用相關性分組、典型變量搜索和分組搜索等方法，達到優化溫度測點分布的目的。Lee等[10]采用相關系數和線性回歸相結合的方法對溫度變量進行優化，以最小殘差平方和作為選擇溫度變量的依據，有效地減少了建模所需的溫度測點。楊建國等[11]提出了數控機床熱誤差分組優化建模方法；苗恩銘等[12-13]利用模糊聚類結合灰色關聯度的方法對溫度敏感點進行了相關研究。

上述研究中均假設溫度敏感點具有穩定性，即對于同一臺數控加工中心，根據在此機床上得到的多組實驗數據，其溫度敏感點計算結果均一致。然而數控機床是一個復雜的裝配體結構，實際運作時，溫度敏感點能否在環境溫度及主軸轉速等加工參數變化狀態下仍保持穩定，如果溫度敏感點發生變動，是否會對模型精度產生影響，這些均未見相關文獻報道。

筆者按照ISO 230-3-2001《機床檢驗通則 第3部分：熱效應的確定》的規定，在Leaderway-V450型數控機床主軸空轉時進行了多批次實驗。采用模糊聚類結合灰色關聯度的方法分析各批次數據的溫度敏感點，根據各批次數據的敏感點變量建立回歸模型，并對模型精度及穩健性進行分析。計算結果證明，不同批次數據的溫度敏感點并不完全相同，且根據敏感點變量建立的補償模型預測穩健性較差。因此，如何在溫度敏感點變動的狀態下，仍保持模型預測精度的穩健性，是數控機床熱誤差建模技術中的重要問題。

為解決上述問題，需要從溫度敏感點選擇與機床熱變形模型預測性能的關系上進行分析。溫度敏感點變動會實質造成模型自變量間的共線性發生變化，進而對模型的預測精度產生影響，也使得熱誤差模型的預測穩健性降低。為此，本文提出具有消除共線性影響功能的主成分回歸(PCR)建模方法，并結合實際機床熱誤差空轉數據對其進行精度檢驗，驗證了該方法的可行性。

1主成分回歸

主成分回歸[14]是利用原自變量的主成分代替原自變量作回歸分析的一種多元統計方法。由于各主成分間互不相關，且保留了原指標的絕大部分信息，因此利用主成分回歸可以有效地解決回歸分析中自變量共線性問題。主成分回歸方法的具體步驟如下：

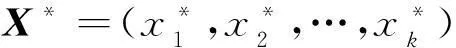
(1)

其中，u1,u2,…,uk為X*的相關系數矩陣的特征向量。

(2)根據累積貢獻率選擇主成分的個數。第g個主成分的累積貢獻率Vccg為

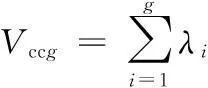
(2)

通常所取的g滿足Vccg≥85%。

(3)將標準化的被解釋變量關于主成分Z1,Z2…,Zg進行回歸，得

(3)

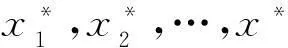
系數βi與原回歸模型參數bi間的關系為

(4)

其中,sy、si分別為原始數據y和xi的標準差，由此得原回歸模型：

2數控機床熱誤差實驗設計

2.1實驗裝置

本文以Leaderway-V450型數控加工中心熱誤差為研究對象。由于該機床的X向和Y向為近似對稱結構，相對于Z向，其熱變形量較小，并且三軸的數據處理方式相同，故本文僅以該機床的主軸Z向熱變形為研究對象，論述溫度敏感點變動性對模型影響特征。各傳感器的安放位置及作用如表1所示，溫度傳感器和電感測微儀具體分布位置如圖1所示。

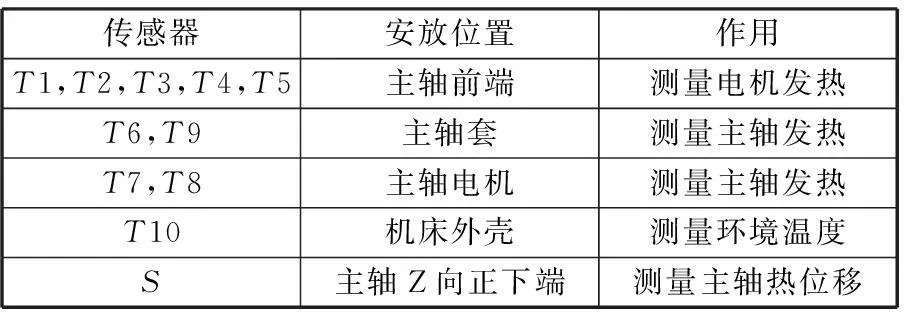
表1　傳感器安放位置及作用

圖1　溫度傳感器和電感測微儀的安放位置

2.2實驗計劃

本文按照ISO230-3-2001規定，實驗采用空轉方式運行，對不同季節進行了多組數據采樣。測量時，溫度和熱誤差同步測量。溫度測量通過數字傳感器DS18B20(測量精度為±0.2 ℃，最高分辨率達0.0625 ℃)進行。實驗采用電感位移傳感器對Z向熱誤差進行測量，電感式位移傳感器的測量精度為±0.5μm。實驗過程中，工作臺保持不動，主軸以恒定轉速(1000r/min、2000r/min、3000r/min、4000r/min)轉動，每隔3min采集一次溫度和熱誤差數據，持續時間在4h以上。實驗數據參數如表2所示，K1～K7批次數據的熱誤差數據如圖2所示。

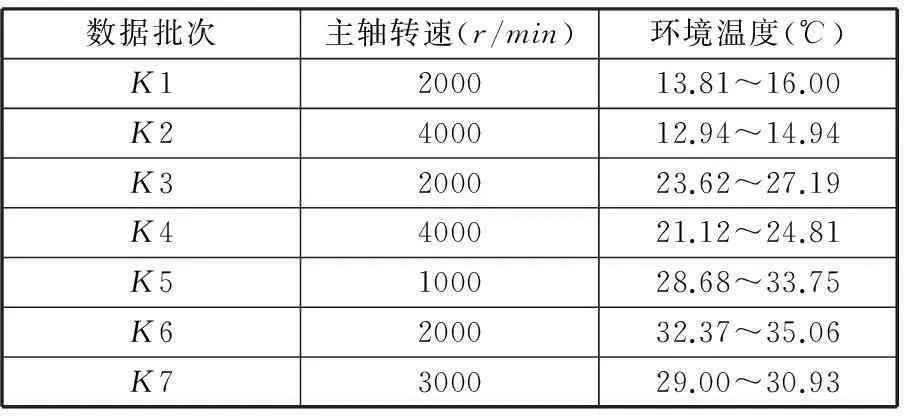
表2　實驗數據參數

圖2　K1～K7批次的熱誤差數據

3溫度敏感點變動性及其影響

3.1溫度敏感點變動性分析

采用模糊聚類結合灰色關聯度的方法[12-13]計算K1～K7批次數據的溫度敏感點，結果如表3所示。由表3可知，K1、K2、K4、K5、K6批次數據的溫度敏感點位置在主軸前軸承和主軸電機位置處，但K3批次數據的溫度敏感點都在主軸電機處，K7批次的溫度敏感點在主軸前軸承和機床外殼(T10)處。各數據的溫度敏感點計算結果不完全相同，即熱誤差補償模型所依據的溫度敏感點位置存在變動性特征。

表3　溫度敏感點計算結果

經分析，溫度敏感點變動性直接來源于數控機床熱源的波動性，其變動性規律尚缺少研究。影響熱源波動性的因素較為復雜，與機床結構特性、工作參數變化、環境溫度等密切相關。那么，溫度敏感點位置的變動是否對回歸模型精度產生影響呢？需要展開討論。

3.2溫度敏感點變動對模型精度影響

實際數控機床熱誤差補償應用時，常根據一次實驗測量數據建立補償模型，故模型自變量應為各數據自身的敏感點變量。

以各數據的敏感點變量為模型自變量，分別建立K1～K7批次數據的多元線性回歸(MLR)模型。K1～K7批次數據的MLR模型分別如下：

(5)

式中，ΔTi為溫度傳感器Ti的溫度值增量；yi為Ki批次數據的模型熱誤差預測值。

根據上述建立的K1～K7批次數據的MLR模型，對K1～K7批次數據進行擬合及預測精度分析，如表4所示。其中，擬合精度是指根據歷史數據所建立的模型，對建模的歷史數據的偏離程度的評價。預測精度是指根據歷史數據所建立的模型，對未參與建模的歷史數據的偏離程度的評價[12-13]。表4中，Mi(i=1,2,…,7)為根據Ki批次數據建立的MLR模型；黑體數字為模型擬合標準差，非黑體數字為模型預測標準差。

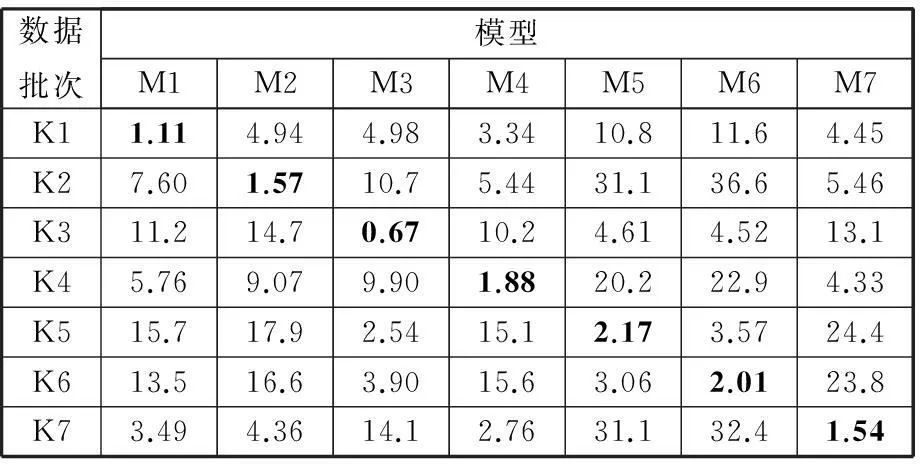
表4　MLR模型擬合及預測效果　μm

由表4可知，MLR模型的擬合標準差分布范圍為0.67～2.17 μm,預測標準差的分布范圍為2.54～36.61 μm。由于建模時使用的是各批次數據自身的敏感點變量，故模型的擬合精度非常高；而模型的預測精度時高時低，預測穩健性不強，則是由于預測數據的溫度敏感點發生了變動，導致模型自變量多重共線性發生變化，對模型的預測穩健性產生了嚴重影響。因此需要采用一種數學算法來控制敏感點變動性造成的模型預測精度損失。

主成分回歸算法可消除自變量共線性影響，故下文將利用該算法建立熱誤差模型，并對其模型精度進行分析。

4主成分回歸建模及精度分析

4.1主成分回歸建模

首先介紹主成分回歸算法的計算步驟。

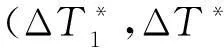
R的特征值和特征向量如表5所示。

表5　特征值和特征向量

根據式(1)得到主成分Z1和Z2的表達式分別為

(6)

由式(2)求主成分Z1和Z2的累計貢獻率分別為96.325%和100%，可知，Z1的累積貢獻率達到96.3250%≥85%，故取主成分個數g=1。

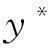
(7)

方程中只包含一個主成分，不存在共線性問題。當方程中存在多個主成分時，通過計算也會發現，這些主成分之間具有不相關性。

將式(6)中第一式代入式(7)得

(8)

根據式(4)將式(8)還原到原始數據y1關于ΔT1、ΔT8的主成分回歸方程：

y1=11.8384+1.5252ΔT1+1.9669ΔT8

(9)

重復上述步驟，計算得到K2～K7批次數據的PCR模型如下:

(10)

4.2PCR模型精度分析

根據上述建立的K1～K7批次數據的PCR模型，對K1～K7批次數據進行擬合及預測精度分析，結果如表6所示。表6中，Mi(i=1,2,…,7)為根據Ki批次數據建立的PCR模型(為便于下文的比較，本文將根據Ki批次數據建立的MLR模型和PCR模型均取名為Mi)；黑體數字為模型擬合標準差，非黑體數字為預測標準差。

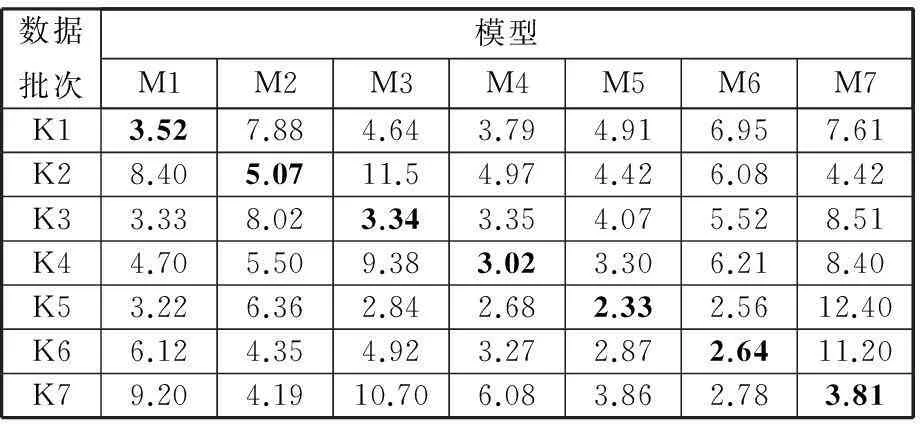
表6　PCR模型擬合及預測效果　μm

由表6可知，PCR模型的擬合標準差分布范圍為2.33～5.07 μm，預測標準差分布范圍為2.56～12.45 μm。

4.3PCR和MLR模型精度的綜合比較

通過對表4和表6中的標準差數據進行進一步分析，得到K1～K7批次數據的MLR模型和PCR模型的擬合效果和預測效果，如表7所示。其中，S為評判擬合精度的參數，其值越小，說明模型擬合精度越高；Mn為評判預測精度平均水平的參數，其值越小，說明模型的平均預測精度越高；Sd為評判預測精度離散程度的參數，其值越小，說明模型預測的穩健性越強。Mn、Sd的計算式分別為

式中，sri(i=1,2,…,6)為各模型的6個預測標準差。

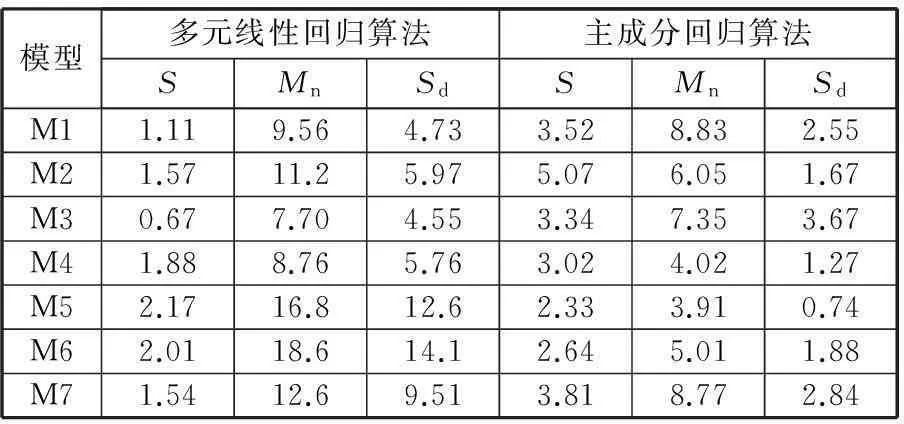
表7　模型擬合及預測效果分析　μm

將表7中數據以二維直方圖形式表示，分別如圖3～圖5所示。

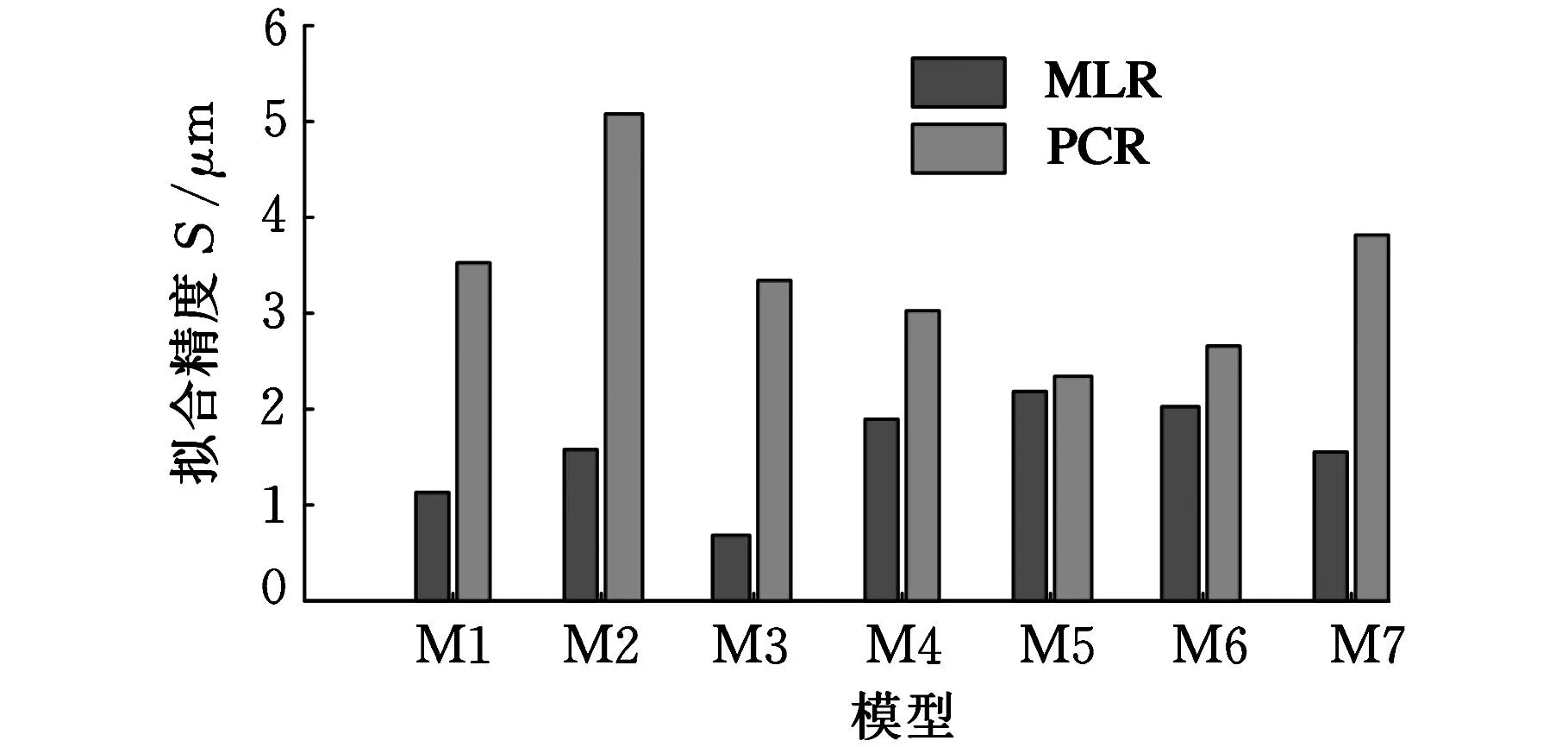
圖3　MLR模型和PCR模型的擬合效果比較

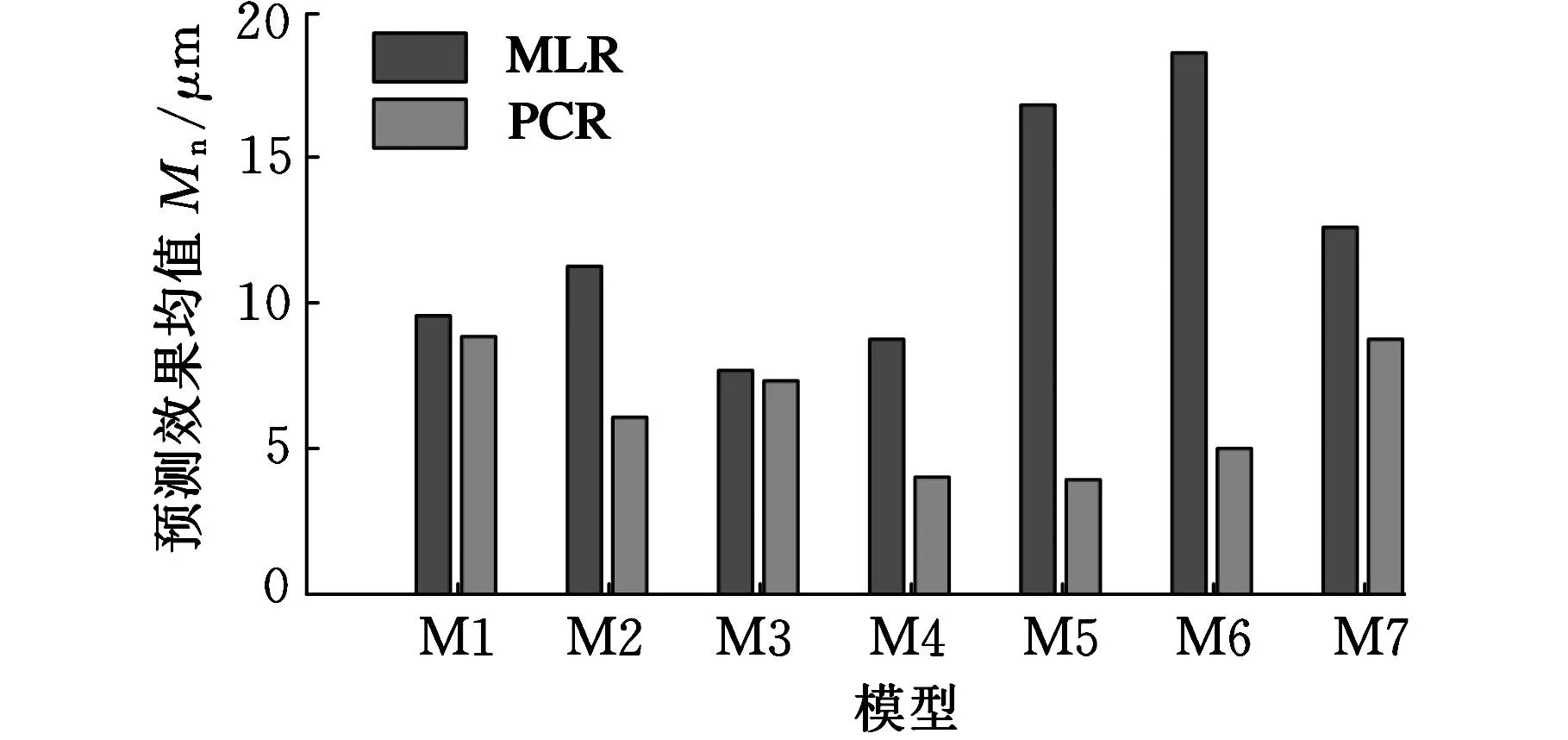
圖4　MLR模型和PCR模型的預測效果均值比較

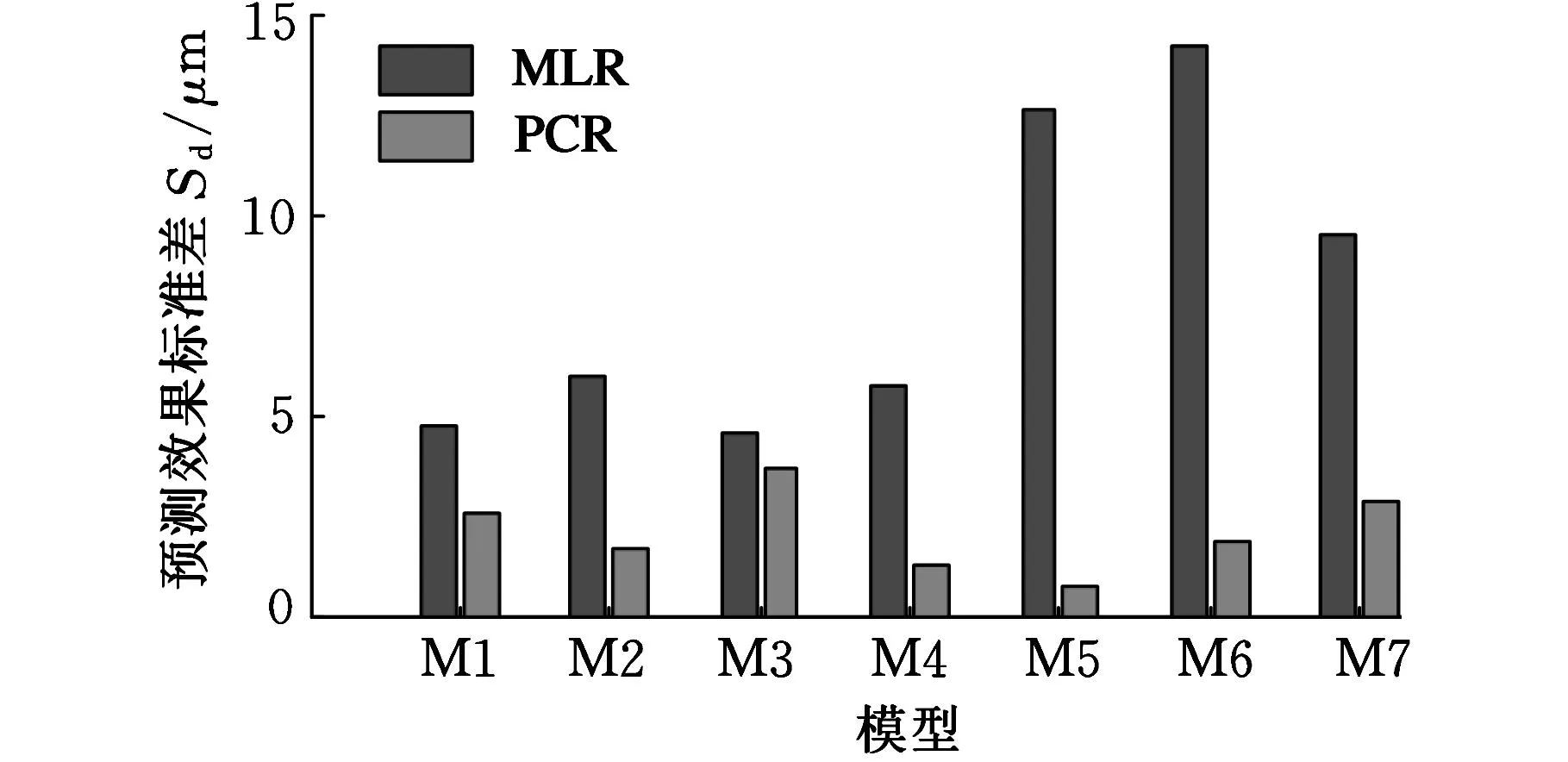
圖5　MLR模型和PCR模型的預測效果標準差比較

綜合表7和圖3～圖5，得到MLR模型和PCR模型的擬合效果范圍、預測效果均值范圍和預測效果標準差范圍如表8所示。

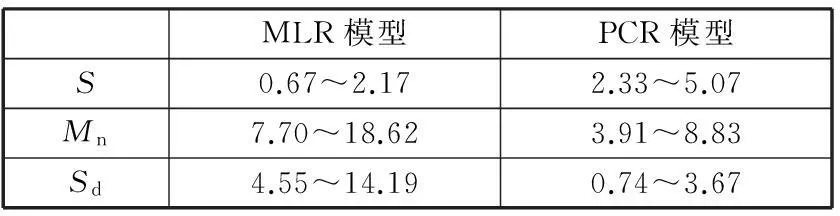
表8　模型擬合效果及預測效果范圍　μm

由表8可知，PCR模型的整體擬合效果低于MLR模型的整體擬合效果，但PCR模型的整體預測效果遠遠高于MLR模型的整體預測效果。究其原因，是因為主成分回歸算法消除了自變量間共線性影響，很好地抑制了敏感點變動對模型預測穩健性產生的影響，使得模型精度和預測穩健性大幅度提高，但其算法本身的訓練精度要稍微低于MLR算法，所以模型擬合精度略低。

然而實際機床熱誤差補償應用時，是利用事先計算好的數學模型對之后的機床運行狀態進行補償，因此更偏重模型預測效果的好壞。故溫度敏感點發生變動時，主成分回歸算法可以明顯降低其對模型精度影響，保證模型具有較好的預測精度和穩健性。

5結論

(1)本文對Leaderway-V450數控加工中心主軸Z向進行了多組熱誤差空轉實驗，并采用模糊聚類結合灰色關聯度的方法對溫度數據進行了溫度敏感點分析。結果表明，熱誤差補償模型所依據的溫度敏感點位置存在變動性特征，造成模型自變量間多重共線性發生變化。通過多元回歸模型的精度分析，驗證了溫度敏感點變動會嚴重影響模型的預測穩健性。

(2)考慮到多重共線性對回歸分析有嚴重影響，故本文提出采用具有消除共線性影響功能的主成分回歸建模方法，并通過實際機床空轉數據給予驗證。結果表明，采用主成分回歸算法建模，顯著降低了溫度敏感點變動對模型穩健性精度的影響。

本文結論只針對Leaderway-V450型數控加工中心，而對不同類型數控機床并未給予深入研究，故實驗結果具有一定局限性。

參考文獻：

[1]Bryan J B．International Status of Thermal Error Research[J]．Ann. CIRP,1990，39(2):645-656．

[2]Aronson R B．War against Thermal Expansion[J]．Manuf. Eng.,1996，116(6):45-50．

[3]Yang S，Yuan J，Ni J.Accuracy Enhancement of a Horizontal Machining Center by Real-time Error Compensation[J]．Journal of Manufacturing Systems，1996，15(2):113-124．

[4]Miao Enming，Gong Yayun，Niu Pengcheng，et al．Robustness of Thermal Error Compensation Modeling Models of CNC Machine Tools[J]. International Journal of Manufacturing Technology，2013，69(9)：2593-2603．

[5]倪軍．數控機床誤差補償研究的回顧及展望[J].中國機械工程，1997，8(1):29-33．

Ni Jun．Review and Forecast for Thermal Errors Compensation of Machine Tools[J].China Mechanical Engineering，1997，8(1):29-33．

[6]Fan Jinmei．Sensor Placement Strategy for Thermal Error Compensation on Machine Tools[J].Chinese Journal of Scientific Instrument,2005：83-84．

[7]Attia M H，Fraser S．A Generalized Modeling Methodology for Optimized Real-time Compensation of Thermal Deformation of Machine Tools and CMM Structures[J]．International Journal of Machine Tools & Manufacture，1999，39(6)：1001-1016．

[8]LoC，YuanJ，NiJ．AnapplicationofReal-timeErrorCompensationonaTurningCenter[J]．InternationalJournalofMachineTools&Manufacture，1995，35(12)：1669-1682．

[9]LoC，YuanJ，NiJ．OptimalTemperatureVariableSelectionbyGroupingApproachforThermalErrorModelingandCompensation[J].Int.J.Mach.ToolsManufact., 1999， 39(9):1383-1396．

[10]LeeJ，YangS．StatisticalOptimizationandAssessmentofaThermalErrorModelforCNCMachinetools[J].InternationalJournationofMachineTools&Manufacture，2002，42(1)：147-155．

[11]楊建國，鄧衛國，任永強，等．機床熱補償中溫度變量分組優化建模[J].中國機械工程，2004，15(6)：478-481．

YangJianguo，DengWeiguo，RenYongqiang，etal．GroupingOptimizationModelingbySelectionofTemperatureVariablesfortheThermalErrorCompensationonMachineTools[J].ChinaMechanicalEngineering，2004，15(6)：478-48．

[12]苗恩銘，龔亞運，成天駒，等．支持向量回歸機在數控加工中心熱誤差建模中的應用[J]. 光學精密工程，2013，21(4)：980-986．

MiaoEnming，GongYayun，ChengTianju，etal．ApplicationofSupportVectorRegressiontoThermalErrorModelingofMachineTools[J].OpticsandPrecisionEngineering，2013，21(4)：980-986．

[13]MiaoEnming，NiuPengcheng，FeiYetai，etal．SelectingTemperature-sensitivePointsandModelingThermalErrorsofMachineTools[J]．J.Chin.Sco.Mech.Eng.,2014，32(6):559-565．

[14]吳誠鷗，秦偉良．近代實用多元統計分析[M].北京：氣象出版社，2007．

(編輯蘇衛國)

Variability of Temperature-sensitive Points and Its Influences for CNC Machine Tools

Miao EnmingLiu YiGao ZenghanLiu Hui

Hefei University of Technology,Hefei,230009

Abstract：In thermal error compensation technology on CNC machine tools, the core issue was to establish mathematical model which might reflect the relationship between incremental temperature and thermal errors of the machine, and the accuracy and robustness of model depended on whether model’s independent variables could reflect the temperature field distribution of CNC accurately, in other words, whether the temperature-sensitive points were accurate and stable. The variability of temperature-sensitive points was proved by analyzing batches of experimental data of air cutting experiments on Leaderway-V450 machine tool spindle Z direction, so it changed the degree of multi-collinearity among temperature variables, caused a serious impact on model’s forecasting accuracy and robustness. Since PCR algorithm might eliminate the influences of multi-collinearity among variables, the modeling method was proposed based on PCR algorithm. And this method was used to practice tests through the experiments of actual machine. The results show, PCR model reduces the effects of changes in temperature-sensitive points on model’s forecasting accuracy significantly, and the model has good forecasting accuracy and robustness.

Key words:CNC machine tool; temperature-sensitive point; multi-collinearity; principal component regression(PCR)

收稿日期：2015-04-20

基金項目：國家自然科學基金資助重大項目(51490660，51490661)；國家自然科學基金資助項目(51175142，E051102)

中圖分類號：TG502.15; TH161

DOI：10.3969/j.issn.1004-132X.2016.03.001

作者簡介：苗恩銘，男，1971年生。合肥工業大學儀器科學與光電工程學院教授、博士研究生導師。主要研究方向為精密機械工程、精度理論、數控機床熱誤差補償、機械熱魯棒性結構設計理論與應用技術。出版專著1部，發表論文50余篇。劉義，男，1994年生。合肥工業大學儀器科學與光電工程學院碩士研究生。高增漢，男，1990年生。合肥工業大學儀器科學與光電工程學院碩士研究生。劉輝，男，1991年生。合肥工業大學儀器科學與光電工程學院碩士研究生。