隨機風作用下風力發電機齒輪傳動系統動載荷計算及統計分析

徐　芳　周志剛

河南科技大學，洛陽，471003

隨機風作用下風力發電機齒輪傳動系統動載荷計算及統計分析

徐芳周志剛

河南科技大學，洛陽，471003

摘要：針對風力發電機齒輪傳動系統在隨機風作用下失效率高的問題，在模擬真實風速的基礎上，建立考慮外部隨機風載及內部齒輪時變嚙合剛度、軸承時變剛度及綜合傳遞誤差等激勵因素的風力發電機齒輪傳動系統齒輪-軸承耦合動力學模型，通過對動力學模型進行仿真計算，得到各齒輪副的動態嚙合力和各支承軸承的動態接觸力。結合有限單元法和赫茲接觸理論，得到關鍵零部件的應力時間歷程，采用雨流計數法對應力時間歷程進行統計分析，得到傳動系統各關鍵零部件承受載荷的應力譜及概率分布函數。研究結果為風力發電機齒輪傳動系統的動態可靠性分析和疲勞壽命預測奠定基礎。

關鍵詞：風力發電機；齒輪傳動系統；動力學；動載荷；統計分析

0引言

在隨機風作用下，風力發電機齒輪傳動系統在外部隨機風載以及內部齒輪綜合嚙合誤差、時變嚙合剛度、軸承時變剛度等激勵的共同作用下，齒輪和軸承相互耦合并承受復雜的隨時間變化的隨機載荷，這是導致風電齒輪傳動系統失效率高和可靠性低的主要原因[1-2]。由于風電齒輪傳動系統承受載荷的時變性和隨機性，使得傳統的機械靜強度可靠性設計和分析方法不能準確反映風電傳動系統的實際情況，必須采用與其載荷特性相適應的動態可靠性分析方法，而獲得精確的動載荷及其統計規律是研究風電傳動系統動態可靠性的基礎。目前，傳動系統齒輪和軸承的動載荷主要通過實測和仿真方式獲得，實測從理論上說較為準確，但測試困難，耗時長，成本高。仿真計算成本低，簡單可行，只需要建立符合實際的風速模型、精細的動力學模型并采用客觀準確的統計方法，就可以得到比較接近實際情況的載荷分布形式和可靠性結果。

目前，針對隨機風速預測模型已有較多研究[3-4]，這些研究大多采用基于概率統計的風速預測方法和基于譜估計的自回歸理論風速預測方法，研究成果在風力機的設計中得到了較好的應用，但預測模型在精度上還無法滿足對風電傳動系統動態性能分析的需要。許多學者針對風力發電機齒輪傳動系統建立了動力學模型[5-6]，但這些研究沒有考慮外部激勵載荷的隨機性和內部軸承剛度的時變性對傳動系統動力學特性及動載荷的影響，這與風力發電機實際運行情況有較大偏差。在風電齒輪傳動系統的可靠性研究方面，秦大同等[7]建立1.5 MW風力發電齒輪傳動系統動力學模型，研究了齒輪傳動系統的可靠性評估問題，但該研究沒有對動載荷進行有效的統計分析，只是將動載荷等效為靜載荷且假定等效載荷符合某種分布，因此其研究結果無法滿足風力發電機特殊工況對可靠性評估的要求。謝里陽等[8]在理論上從地域位置和時間兩個方面描述了風力發電機載荷歷程的概率特性。

本文在建立隨機風速模型和精確的傳動系統齒輪-軸承耦合動力學模型的基礎上，獲得外部隨機風載和內部齒輪-滾動軸承耦合的共同作用下系統關鍵零部件(齒輪和軸承)的動載荷及相應的應力時間歷程，進而結合數理統計理論得到傳動系統各構件承受的應力譜及概率分布函數，為進一步研究風電傳動系統的動態可靠性及疲勞壽命預測奠定基礎。

1傳動系統外部隨機風載荷計算

風場隨機風速的大小及其動態變化對風電齒輪箱的工作性能和可靠性有重要影響。因此，為了研究風力發電機齒輪傳動系統的動力學特性和可靠性，必須建立與實際風速相符合的風速模型，在模擬實際風速變化的條件下研究風力發電機齒輪傳動系統的動態性能和疲勞壽命。

采用徑向基核函數支持向量機(support vector machines，SVM)模擬方法對經過校正和標準化變換后的實測風速值進行分類和學習，通過交叉檢驗方法選取徑向基函數的最佳寬度，建立基于加權最小二乘支持向量機(weight sparse least squares support vector machines，WSLS-SVM)方法的風力發電機風速預測模型，可得到具有較高估計精度的風速值[9]。將該風速時間歷程所對應的轉矩時間歷程作為風力發電機行星齒輪傳動系統的輸入外載荷，可為進行風力發電機傳動系統的動力學特性、動載荷計算和壽命預測提供基礎。

用WSLS-SVM風速模型模擬的風速引起的時變載荷作為系統的外部激勵。根據空氣動力學理論可以得到

(1)

式中，P0為葉輪的輸出功率(即傳動系統的輸入功率)，W；ρ為空氣密度，kg/m3; r為葉輪半徑，m；CP為風能利用系數；v為風速，m/s。

系統的輸入端轉矩Tin和輸出端轉矩Tout為

(2)

式中，ω為風輪的角速度，rad/s；i為齒輪傳動系統的傳動比。

2傳動系統齒輪-軸承耦合動力學模型及動載荷計算

2.1齒輪-軸承耦合動力學模型

目前1.5 MW風力發電機齒輪傳動大都采用NGW型行星傳動和兩級平行軸傳動的方式，其結構模型如圖1所示。

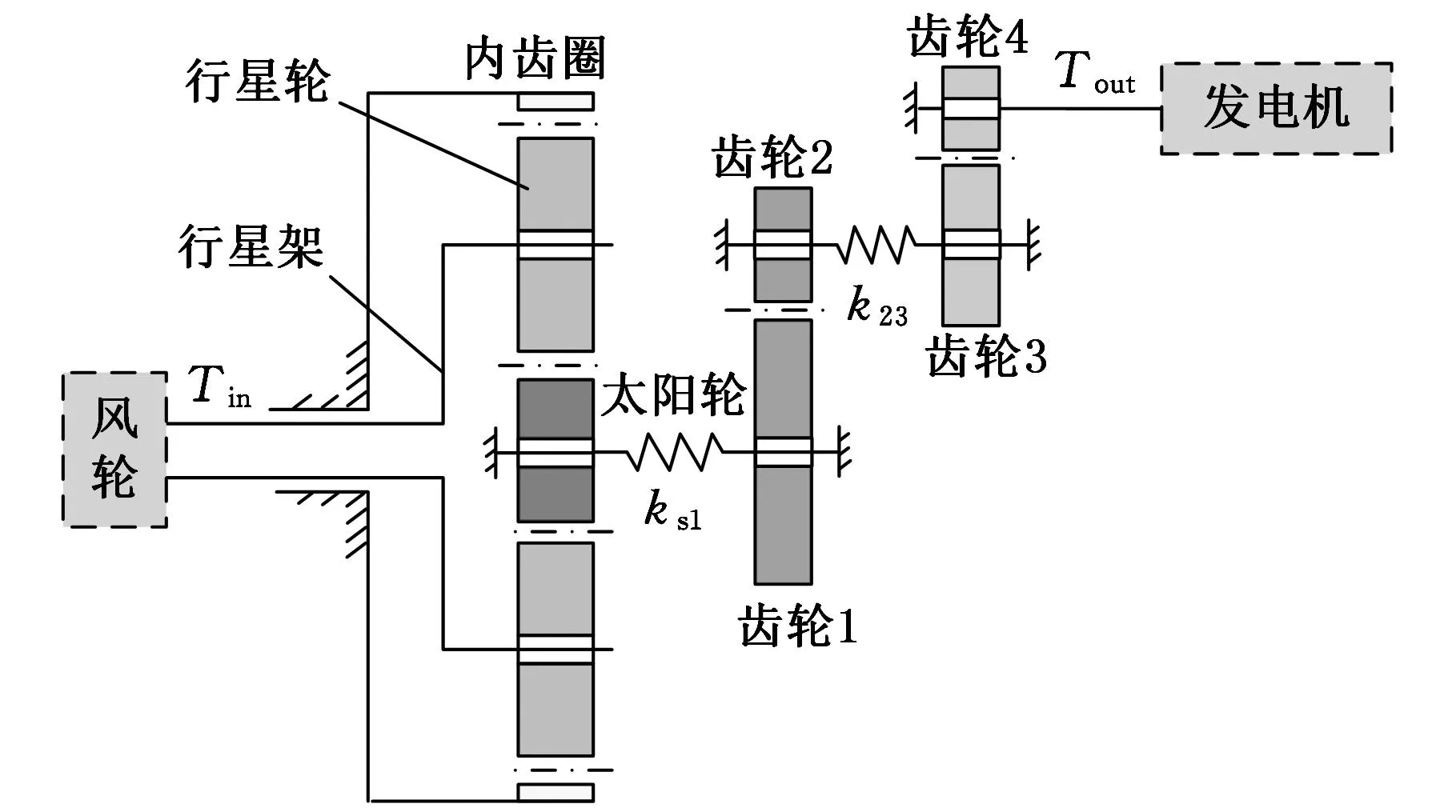
圖1　風電齒輪傳動系統簡圖

為簡化模型和計算，采用文獻[10-12]的方法，假定傳動系統中行星傳動級的三個行星輪沿圓周均布，且具有相同的物理和幾何參數，將齒輪副之間的嚙合模擬為具有時變剛度的彈簧，并考慮齒輪的綜合嚙合誤差、滾動軸承時變剛度等因素，采用集中質量參數法建立圖2所示的風力發電機齒輪傳動系統的平移-扭轉動力學模型，圖中，s、c、r(包括下標)分別表示太陽輪、行星架、內齒圈，p1、p2、p3表示行星輪。模型中內部激勵的計算方法及其詳細過程參見文獻[13]。

根據拉格朗日方程推導出矩陣形式的系統彈性動力學方程為

(3)

q=[xcycucxsysusζp1ηp1up1…

ζpnηpnupnx1y1u1…x4y4u4]T

式中，M為系統廣義質量矩陣；Kb(t)為支承軸承剛度矩陣；Km(t)為齒輪嚙合剛度矩陣；G為陀螺矩陣；Kω為向心剛度矩陣；ωc為行星架角速度；T(t)為系統的外部激勵；F(t)為系統的內部激勵；q為系統廣義坐標列陣；xk、yk、uk(k=c,s,1,2,3,4)分別為各構件在x、y方向和扭轉方向上的位移；ζpj、ηpj、upj(j=1,2,3)分別為各行星輪在ζ、η方向和扭轉方向上的位移。

式(3)中各列陣和矩陣的維數均為27。

2.2模型求解及動載荷計算

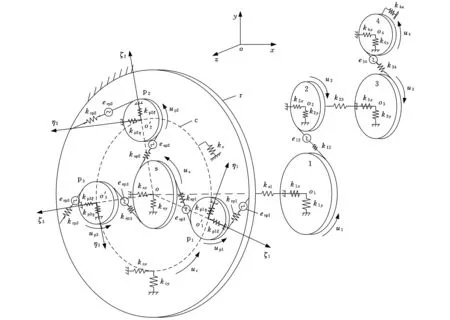
圖2　風力發電機齒輪傳動系統耦合動力學模型

本文采用Runge-Kutta數值計算方法，通過MATLAB編程實現對風力發電機齒輪傳動系統動力學模型的數值求解。其實現過程是，先將建立的矩陣形式微分方程轉換為顯式一階微分方程組，通過MATLAB提供的數值解法求解器直接編程求解，然后通過求解傳動系統動力學模型得到隨機風作用下系統各齒輪和各軸承的振動位移，則輪齒間的動態嚙合力Fd為

(4)

δ=(δspj,δrpj,δ12,δ34)j=1,2,3

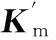
由式(4)可求得系統各齒輪副的動態嚙合力。同理，根據文獻[10]中的非線性軸承力的計算方法得到系統各支承軸承的非線性動態接觸力。

3傳動系統動態接觸應力計算及統計分析

3.1關鍵零部件的動態接觸應力計算

基于有限元方法和赫茲接觸理論計算得到傳動系統關鍵零部件齒輪和軸承在靜載荷條件下的彈性接觸應力，采用準靜態方法得到動態接觸應力時間歷程，即根據靜載荷下的彈性應力和動態載荷時間歷程求得動態應力時間歷程，為動態可靠性分析提供基礎。

(1)齒輪副最大接觸應力。將齒輪傳動系統的CAD模型導入有限元軟件環境中，通過定義材料屬性和接觸對、劃分網格、施加載荷等步驟，對有限元模型進行分析求解，得到傳動系統各齒輪副最大接觸應力。

(2)滾動軸承的最大接觸應力。滾動軸承主要靠滾動體與滾道的接觸而支承并傳遞載荷，滾動軸承內部的接觸問題基本滿足赫茲理論所作的假設，因此可以用赫茲接觸理論計算滾動軸承的最大赫茲接觸應力pmax[14]:

(5)

其中，Q為軸承內鋼球承受的載荷；ea=0.023 63μ，eb=0.023 63υ，μ、υ為接觸區域尺寸，可通過赫茲接觸系數表線性插值求得；對于軸承鋼，εE可取值為1。

(3)基于準靜態法的動態接觸應力計算。由風力發電機齒輪傳動系統齒輪-軸承耦合動力學模型經仿真計算，得到齒輪嚙合力及軸承力的變化時間歷程，結合齒輪和軸承的最大接觸應力，通過下式即可計算得到齒輪嚙合力及軸承力的應力-時間歷程：

(6)

式中，pFEA為定義的靜態載荷；σ為靜態載荷所引起的彈性應力；p(t)為動態載荷-時間歷程；σ(t)為應力-時間歷程。

齒輪和軸承的動態時間歷程是在最大靜應力的基礎上獲得的，因此，該方法為準靜態方法，可為隨機風作用下風電齒輪傳動系統的動載荷統計及動態可靠性模型建立奠定基礎。

3.2系統關鍵零部件應力-時間歷程的統計分析

通過有限單元法和赫茲接觸理論得到的傳動系統中齒輪和軸承的動態接觸應力-時間歷程也是一個隨機應力。目前，對這種不重復、無規則變化的動態應力的作用規律無法用數學公式表達，只能用統計分析的方法進行描述，而對隨機應力進行循環計數是進行統計分析的前提。通過循環計數將復雜的應力-時間歷程簡化為具有循環概念的簡單載荷，將應力-時間歷程離散成一系列的峰谷值，經循環計數處理后就可以得到載荷幅值、均值和相應頻次的重要關系，通過對計數結果進行統計分析，得到動態接觸應力的概率分布特征，為零件和系統的動態可靠性分析、疲勞強度計算、疲勞壽命預測及疲勞壽命試驗提供基礎。

目前，雨流計數法是國內外學者普遍認為符合疲勞損傷規律的一種隨機載荷的循環計數方法，在工程實際中得到了廣泛應用。因此，本文使用雨流計數法對傳動系統齒輪副和軸承的動態接觸應力-時間歷程進行計數，并對計數結果進行統計分析和K-S假設檢驗，得到各齒輪副接觸應力和滾動軸承接觸應力近似服從正態分布的結果，為傳動系統的動態可靠性模型的建立及分析提供基礎。

通過以上方法得到傳動系統中齒輪和軸承的動態接觸應力的分布形式。由于傳動系統的輸入風載荷是由符合實際的隨機風速模型得到的，因此，通過動力學模型、循環計數及統計分析得到的齒輪和軸承的動態接觸應力分布形式也較為符合實際情況，從而為開展基于動力學的傳動系統動態可靠性分析和疲勞壽命預測提供可靠的基礎，使所建立的動態可靠性模型和疲勞壽命預測模型更加符合實際，從而提高動態可靠性分析結果和疲勞壽命預測結果的可信度。

4實例分析

用于仿真分析的風力發電機設計參數如下：額定功率1.5MW，葉輪直徑70.4m，葉輪設計轉速14.93r/min，風場平均風速12.5m/s，風密度1.225kg/m3，風能利用系數0.32，傳動系統的傳動比98.47。傳動系統中齒輪和滾動軸承的相關參數見表1和表2。其中，齒輪材料為20GrMnTi，精度等級為6級。軸承材料為高強度軸承鋼GCr15SiMnA。

由隨機風速模型及空氣動力學原理，得到風力發電機行星齒輪傳動系統的輸入轉矩如圖3所示，為方便求解，截取前10s的系統輸入轉矩作為仿真模型的輸入轉矩激勵，如圖4所示。

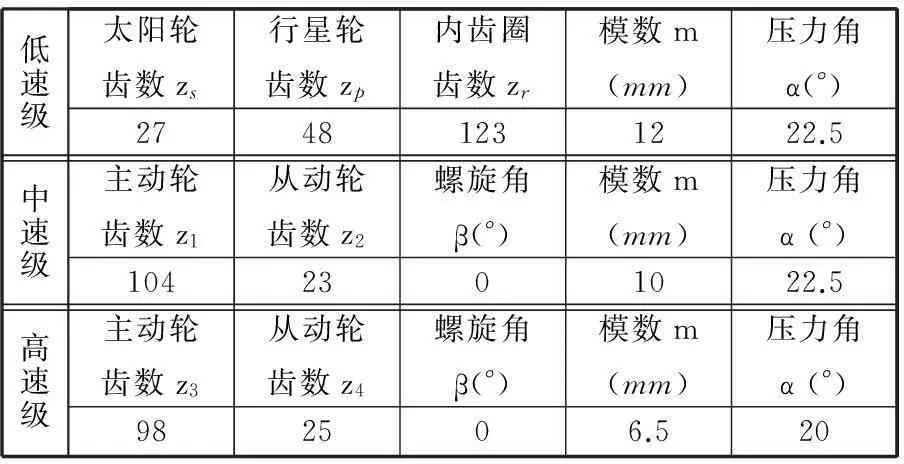
表1　風力發電機齒輪傳動系統幾何參數

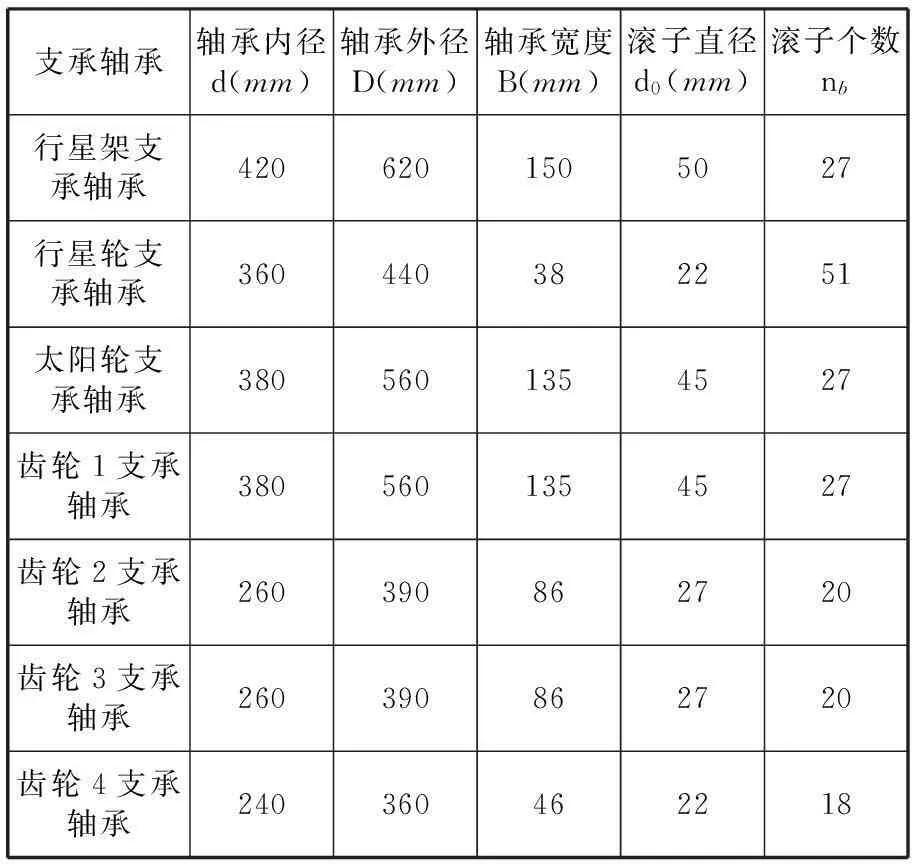
表2　滾動軸承的主要幾何參數

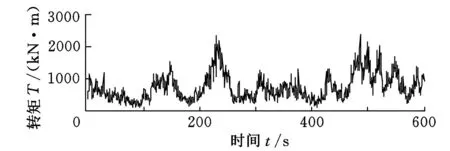
圖3　系統輸入轉矩激勵

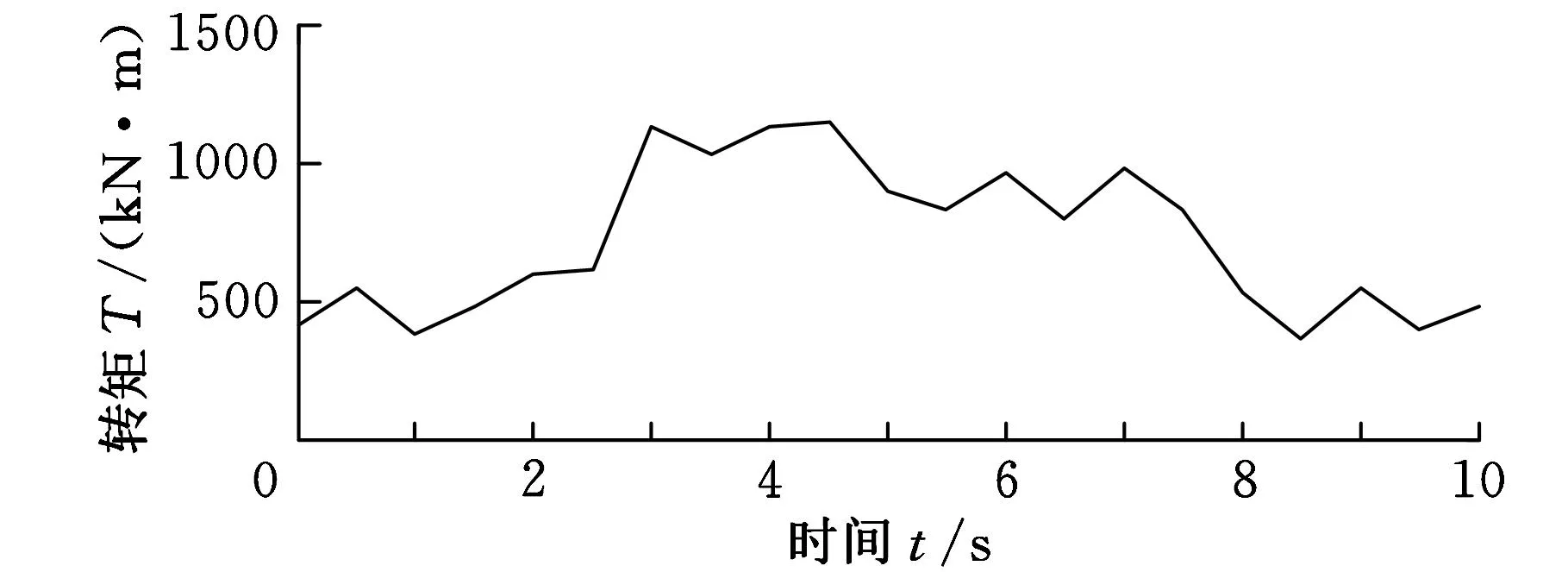
圖4　前10 s轉矩時間歷程曲線

用數值積分方法對系統動力學模型進行仿真計算，可以求得系統各齒輪副的動態嚙合力和各支承軸承的動態接觸力，在此基礎上，基于準靜態方法得到相應的動態接觸應力-時間歷程。圖5和圖6示出了隨機風載作用下系統各齒輪副之間的動態接觸應力時間歷程；限于篇幅，這里僅給出行星輪和齒輪4的支承軸承的動態接觸應力時間歷程，如圖7所示。

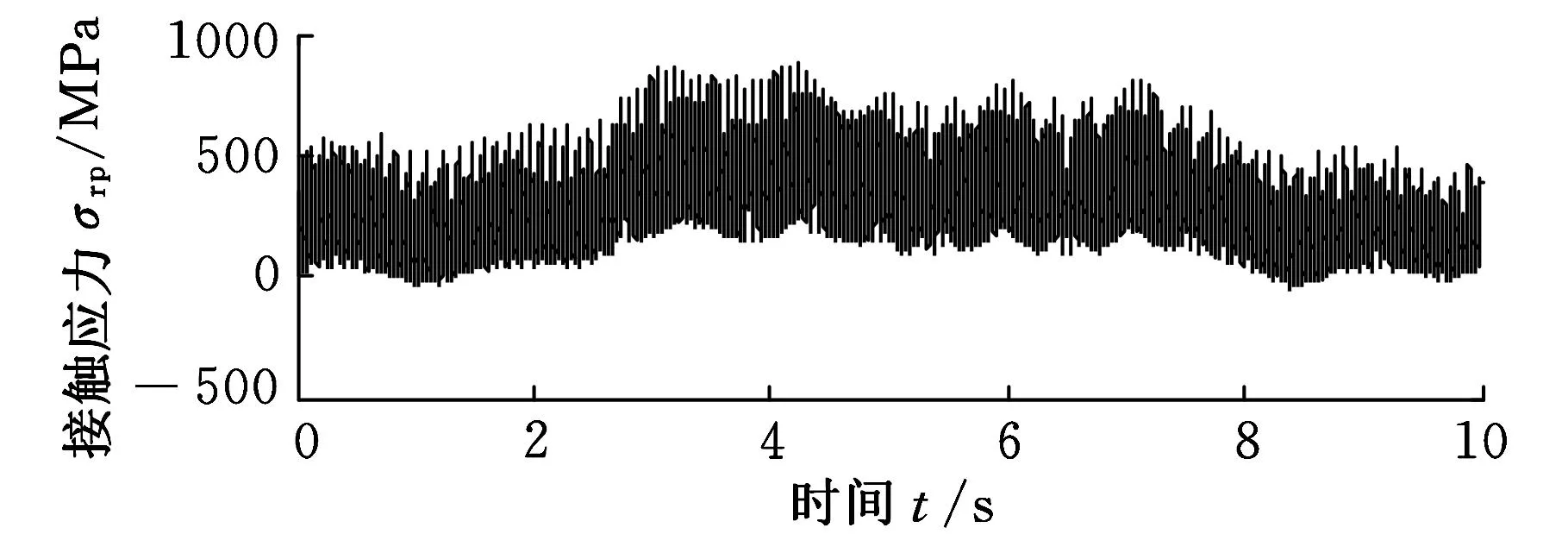
(b)內齒圈與行星輪接觸應力-時間歷程圖5　行星級齒輪副的動態接觸應力

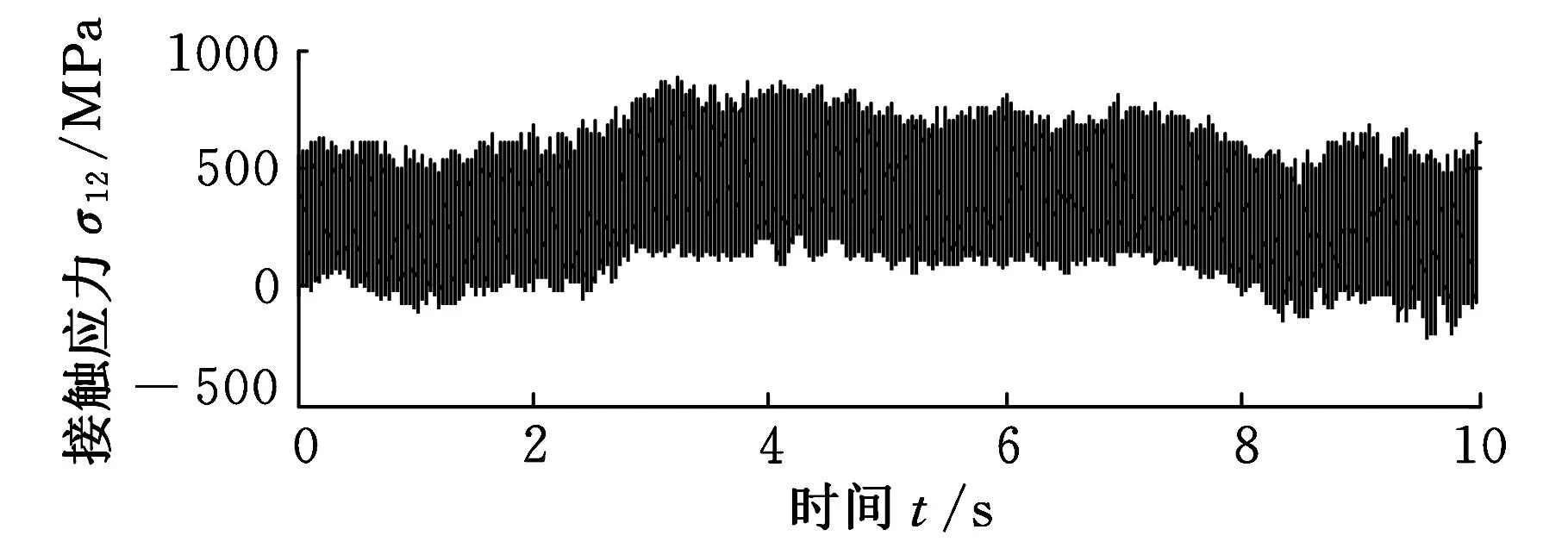
(a)齒輪1與齒輪2接觸應力-時間歷程

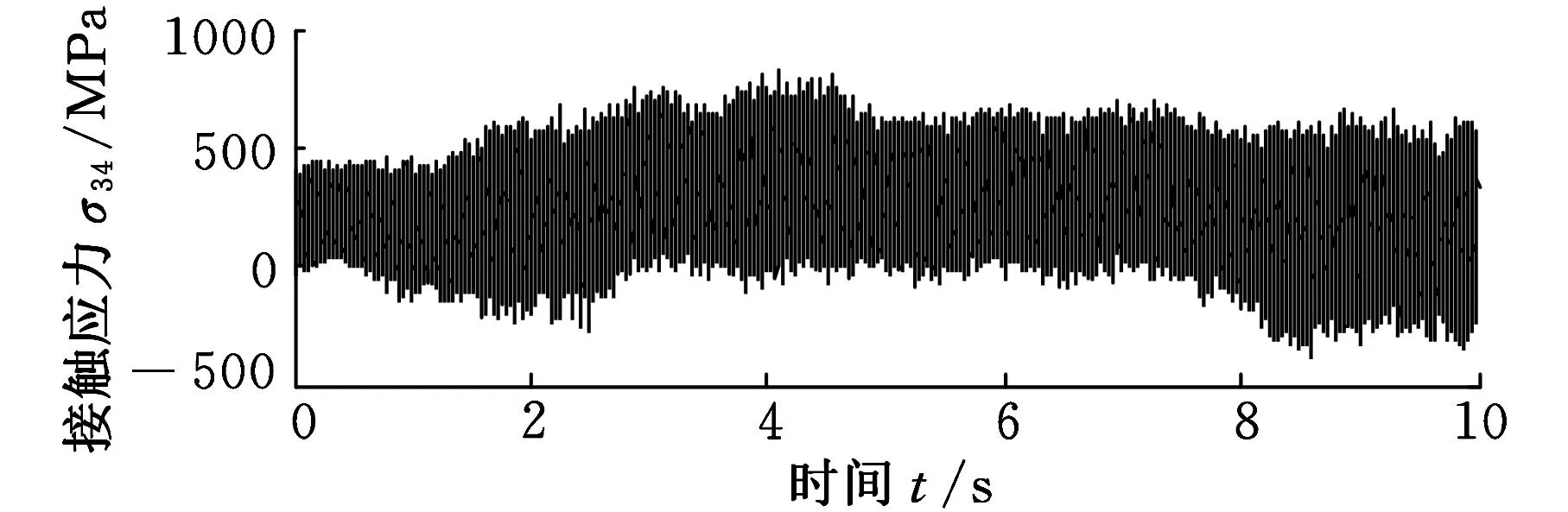
(b)齒輪3與齒輪4接觸應力-時間歷程圖6　平行軸級齒輪副的動態接觸應力

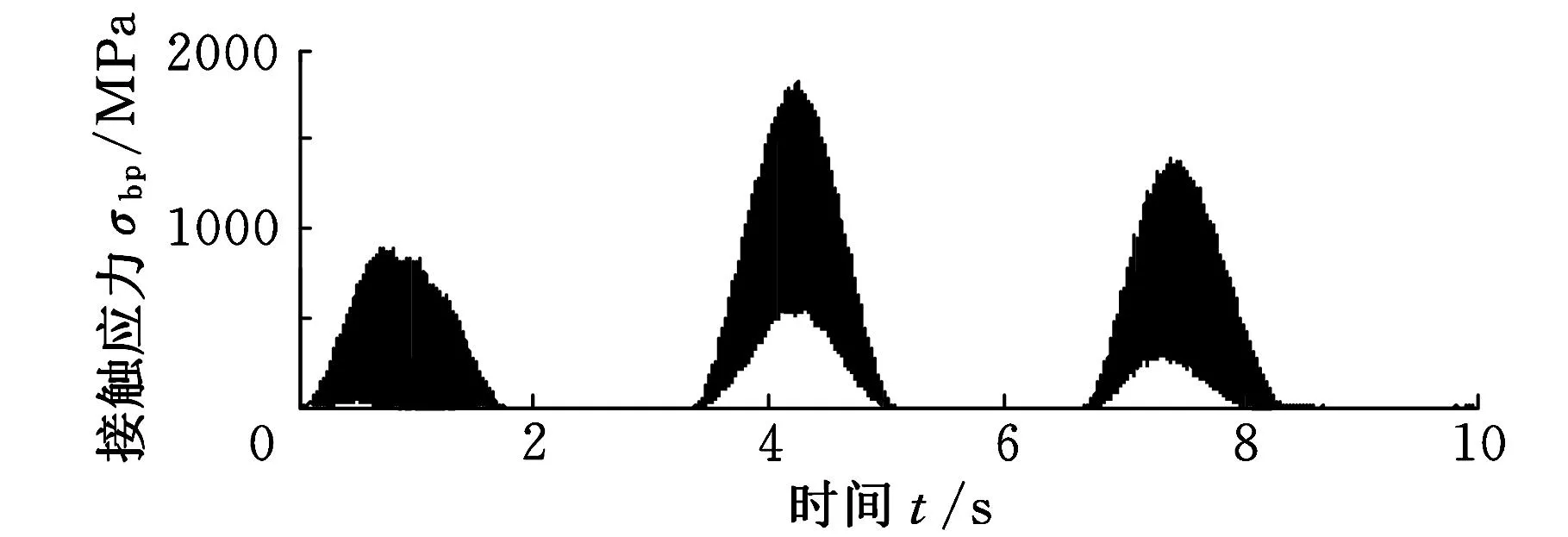
(a)行星輪支承軸承接觸應力-時間歷程

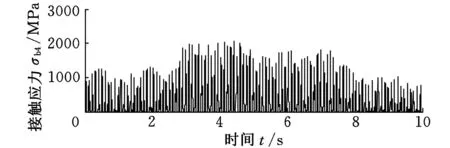
(b)齒輪4支承軸承接觸應力-時間歷程圖7　行星輪和齒輪4支承軸承接觸應力時間歷程

圖8和圖9所示為齒輪傳動系統各齒輪副和各支承軸承的接觸應力譜。表3給出了具體分布形式及參數。

5結論

(1)通過模擬實際隨機風速獲得了由隨機風速引起的傳動系統輸入轉矩，并將其作為風力發電機齒輪傳動系統的外部激勵引入動力學模型中，使動力學模型的求解結果更加接近于工程實際。

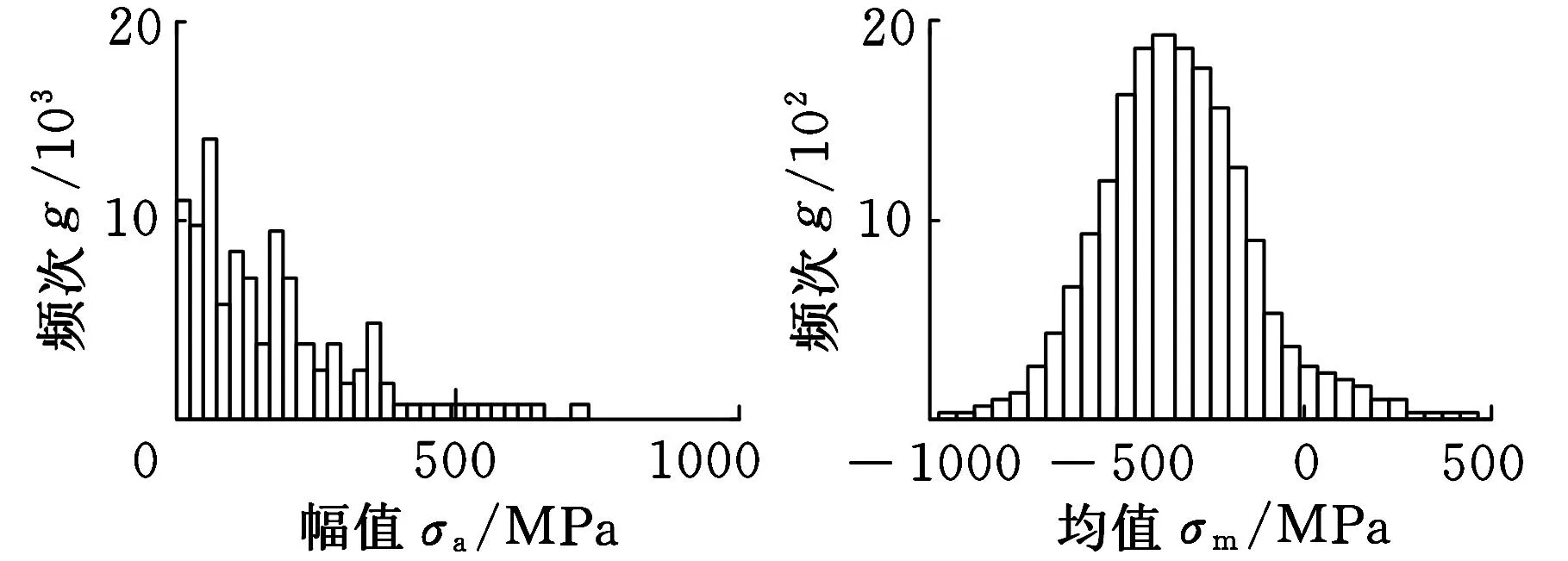
(a)行星輪太陽輪　　　(b)行星輪太陽輪　　　接觸應力幅值統計　　　接觸應力均值統計

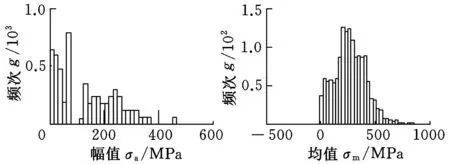
(c)內齒圈和行星輪　　　(d)內齒圈和行星輪　　　接觸應力幅值統計　　　接觸應力均值統計

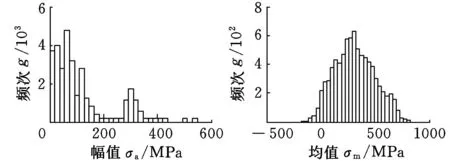
(e)齒輪1齒輪2　　　(f)齒輪1齒輪2　　　接觸應力幅值統計　　　接觸應力均值統計

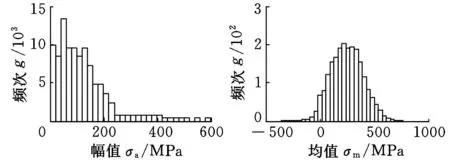
(g)齒輪3齒輪4　　　(h)齒輪3齒輪4　　　接觸應力幅值統計　　　接觸應力均值統計圖8　各齒輪副接觸應力譜

(a)行星輪支承軸承　　　(b)行星輪支承軸承　　　接觸應力幅值統計　　　接觸應力均值統計

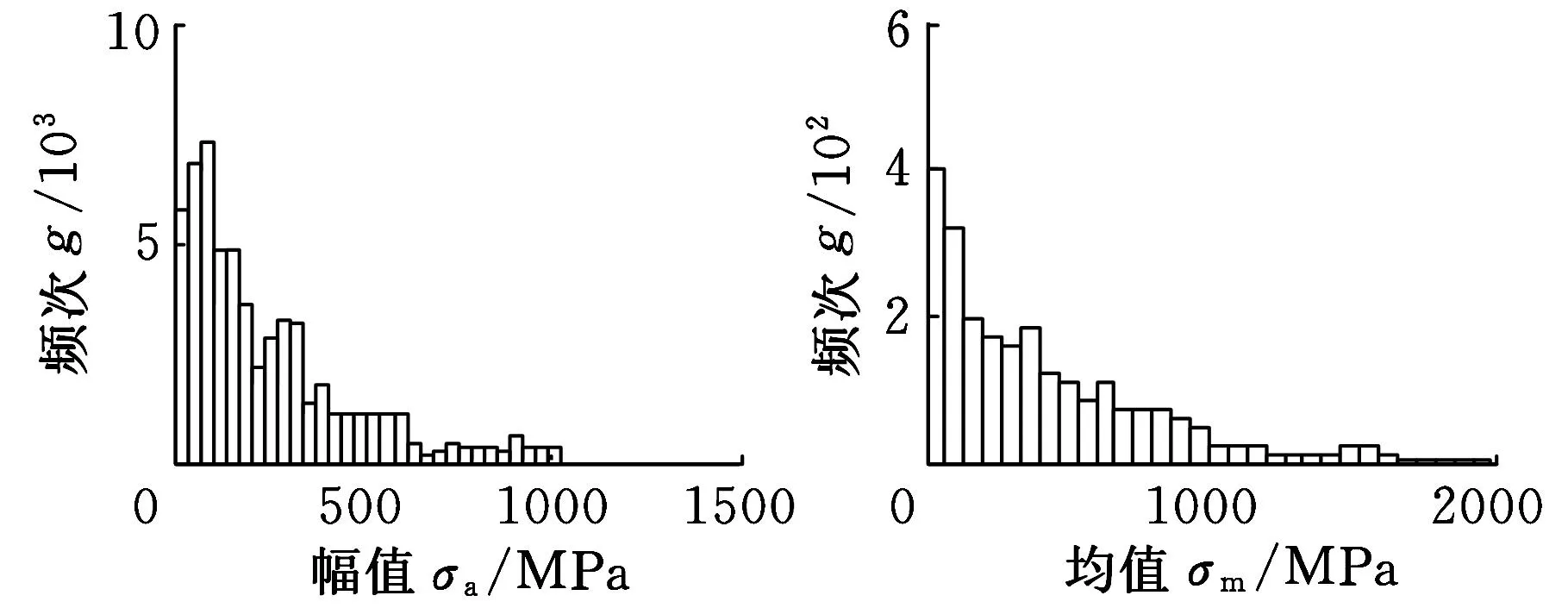
(c)齒輪4支承軸承　　　(d)齒輪4支承軸承　　　接觸應力幅值統計　　　接觸應力均值統計圖9　行星輪和齒輪4支承軸承的應力譜

傳動系統各零件應力(載荷)均值(MPa)應力(載荷)標準差(MPa)內齒圈45231.5行星輪46528.2太陽輪48325齒輪147534.8齒輪246738.2齒輪347845.7齒輪449262.3行星架軸承53217.5行星輪軸承50823.8太陽輪軸承45434齒輪1支承軸承47236齒輪2支承軸承46938.6齒輪3支承軸承48339.4齒輪4支承軸承49542.1

(2)基于動力學模型和準靜態方法求得的系統各齒輪副和各軸承的動態接觸應力-時間歷程可為精確地對系統動載荷進行統計分析提供基礎數據。

(3)在隨機風作用下進行基于動力學的傳動系統動載荷的統計分析，可以獲得較為準確的傳動系統各關鍵零部件動態接觸應力的分布規律，克服了根據經驗假設載荷分布規律所帶來的計算精度不高的缺陷，提高了系統可靠度計算的精度，為進一步建立風電傳動系統動態可靠性模型提供基礎。

參考文獻：

[1]GuoY，KellerJ，LaCavaW.PlanetaryGearLoadSharingofWindTurbineDrivetrainsSubjectedtoNon-torqueLoads[J].WindEnergy，2014(4)：757-768.

[2]MusialW，ButterfieldS，McniffB.ImprovingWindTurbineGearboxReliability[C]//EuropeanWindEnergyConference.Milano，2007: 1-13.

[3]李建林，肖志東，梁亮，等. 風能-可再生能源與環境[M]. 北京:人民郵電出版社, 2010.

[4]竇真蘭，王晗，張秋瓊，等．虛擬風場和風力機模擬系統的實驗研究[J].中國電機工程學報,2011，31(20): 127-135.

DouZhenlan,WangHan,ZhangQiuqiong,etal.ExperimentalResearchonVirtualWindFarmandWindTurbineEmulatorSystem[J].ProceedingsoftheChineseSocietyforElectricalEngineering, 2011, 31(20): 127-135.

[5]PeetersJLM,SasP,VandepitteD.AnalysisofInternalDriveTrainDynamicsinaWindTurbine[J].WindEnergy, 2005,9:141-161.

[6]LiewaHV,LimTC.AnalysisofTime-varyingRollingElementBearingCharacteristics[J].JournalofSoundandVibration, 2005,283:1163-1179.

[7]秦大同，邢子坤，王建宏.基于動力學和可靠性的風力發電齒輪傳動系統參數優化設計[J].機械工程學報，2008，44(7)：24-31.

QinDatong，XingZikun，WangJianhong.OptimizationDesignofSystemParametersoftheGearTransmissionofWindTurbineBasedonDynamicsandReliability[J].JournalofMechanicalEngineering，2008，44(7)：24-31.

[8]謝里陽，劉建中，吳寧祥，等. 風電裝備傳動系統及零部件疲勞可靠性評估方法[J].機械工程學報，2014,50(11)：1-8.

XieLiyang，LiuJianzhong，WuNingxiang，etal.FatigueReliabilityEvaluationMethodforGearboxComponentandSystemofWindTurbine[J].JournalofMechanicalEngineering，2014，50(11)：1-8.

[9]TascikaraogluA,UzunogluM.AReviewofCombinedApproachesforPredictionofShort-termWindSpeedandPower[J].RenewableandSustainableEnergyReviews, 2014, 34(6):243-254.

[10]秦大同，周志剛，楊軍，等. 隨機風載作用下風力發電機齒輪傳動系統動態可靠性分析[J]. 機械工程學報，2012, 48(3): 1- 8.

QinDatong，ZhouZhigang，YangJun，etal.Time-dependentReliabilityAnalysisofGearTransmissionSystemofWindTurbineunderStochasticWindLoad[J].JournalofMechanicalEngineering, 2012, 48(3):1- 8.

[11]LimTC,SinghR.VibrationTransmissionthroughRollingElementBearings,PartⅡ:SystemStudies[J].JournalofSoundandVibration, 1990,139(2): 201-205.

[12]LinJ.AnalyticalInvestigationofPlanetaryGearDynamics[D].Columbus:theOhioStateUniversity, 2000.

[13]徐芳，周志剛，李迎春，等. 基于動力學的風電增速箱多級齒輪傳動系統可靠性評估[J].中國機械工程，2014,25(9)：1219-1224.

XuFang，ZhouZhigang，LiYingchun，etal.ReliabilityAssessmentofMulti-stageGearsTransmissionSystemofWindPowerGrowthGearboxBasedonDynamics[J].ChinaMechanicalEngineering，2014，25(9)：1219-1224.

[14]岡本純三.球軸承的設計計算[M]. 黃志強，譯.北京：機械工業出版社，2003.

(編輯蘇衛國)

Dynamic Load Calculation and Statistical Analysis of Gear Transmission System of Wind Turbine under Stochastic Wind Loading

Xu FangZhou Zhigang

Henan University of Science and Technology,Luoyang,Henan,471003

Abstract:Aiming at the problems of high failure rate of wind turbines gear transmission system under the stochastic wind speed conditions, a dynamics model of gear transmission system coupled with bearing of wind turbine was established on the basis of simulating real wind speed, and the external random wind load and internal excitations such as time-varying mesh stiffness of gear pair, time-varying stiffness of rolling element bearings and integrated transmission errors were considered in the model. Numerical method was used to simulate the dynamics model, the dynamic meshing forces of each gear pair as well as the dynamic contact forces of each bearing were obtained. Then, the stress spectrum and the probability distribution function of the loads acting on the key parts of transmission system were obtained by statistic the stress-time history curves which was obtained by using the finite element method and the Hertz contact theory. This research results lay a foundation for dynamic reliability analysis and fatigue life prediction of the gear transmission system of a wind turbine.

Key words：wind turbine; gear transmission system; dynamics；dynamic load; statistical analysis

收稿日期：2015-04-14

基金項目：國家自然科學基金資助項目(51305126)；河南省教育廳科學技術研究重點項目(13A460274)

中圖分類號：TH132.41；TK83

DOI：10.3969/j.issn.1004-132X.2016.03.002

作者簡介：徐芳，女，1980年生。河南科技大學機電工程學院講師。研究方向為機械傳動系統動力學與可靠性、機械系統的計算機仿真。周志剛(通信作者)，男，1978年生。河南科技大學車輛與交通工程學院副教授、博士。