三臂機器人在軌動力學仿真

黃晉英　杜為民　李　輝　蔣志宏　楊　歡

1.北京理工大學，北京，1010081　　2.中北大學，太原，0300513.中國民用航空河南空管分局，鄭州，451162

三臂機器人在軌動力學仿真

黃晉英1,2杜為民3李輝1蔣志宏1楊歡2

1.北京理工大學，北京，10100812.中北大學，太原，0300513.中國民用航空河南空管分局，鄭州，451162

摘要：根據航天機器人太空作業的需要，設計了三臂機器人簡化模型，應用D-H方法建立了坐標變換矩陣，推導了該機器人的運動學方程。基于ADAMS虛擬樣機技術，分別在三種重力場環境下，對機器人的爬桿過程進行仿真，得到了機械手攀爬過程受力曲線，分析了影響機械手夾持力的主要因素，從而為這類機器人的設計提供參考。

關鍵詞：機器人；在軌；仿真；夾持力

0引言

太空環境極其惡劣，用機器人代替宇航員出艙完成裝配、維修和搬運等工作十分必要[1-2]。空間環境與地面環境最大的區別是微重力,在微重力環境下，機器人處于漂浮狀態，因此地面看似簡單的工作將變得難以實現，其動力學行為與地面有較大差別，其運動學控制較為困難。多臂機器人與雙臂機器人相比，多余的手臂可作為工作中的基座，從而克服了上述難題。三臂機器人可在結構上克服腿、臂獨立結構構型機器人本體機構質量大、結構復雜等缺點，適用于太空作業，正日益引起人們的關注[3-4]。然而，這類空間機器人的研究仍處于起步階段，本研究的目的就是通過機器人的在軌仿真，分析機器人在軌運動中的動力學行為，為其設計和應用提供參考。

1三臂機器人的系統模型

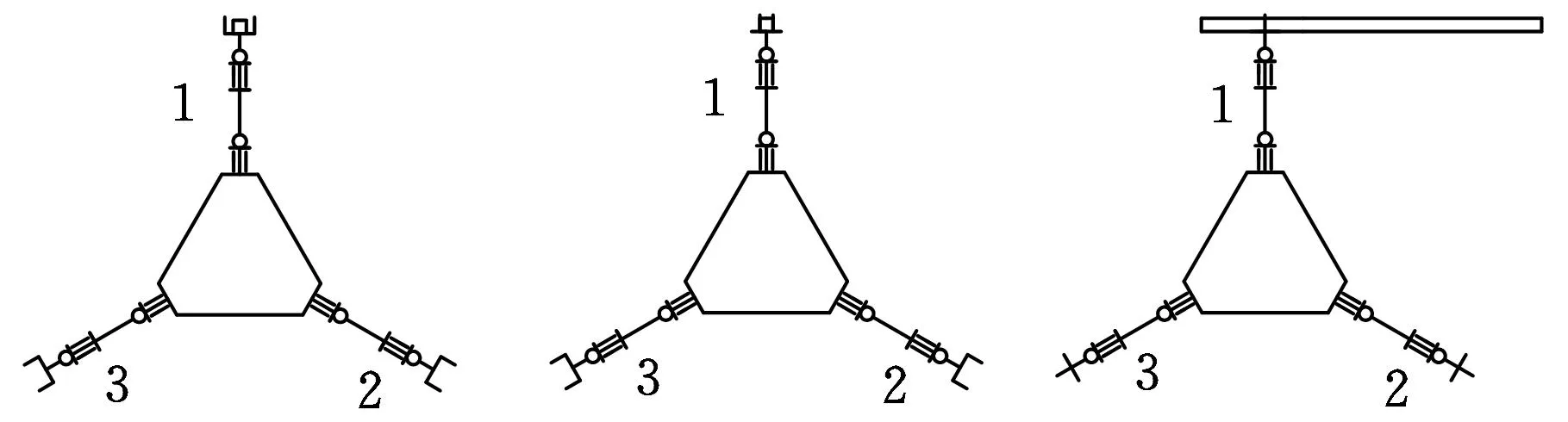
空間三臂機器人的簡化模型如圖1所示，其本體結構為一等邊三角形，擁有3條完全相同的手臂。每條手臂由一組(2只)機械手、小臂和大臂組成，其上的腰關節、大臂關節、肘關節和小臂關節形成4個轉動自由度，機械手的2只手掌與其軌道形成2個移動自由度，3條手臂共計18個自由度。工作時，由3條手臂交替攀爬航天器上設置的扶手到達指定位置，然后其中一條手臂固定在扶手上，其余兩條手臂完成指定工作。這種三臂機構可使機器人具有多種靈活的運動步態和操作方式以適應不同的工況，極大地滿足了空間機器人太空中工作的要求[5-6]。

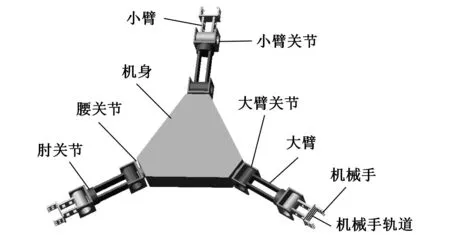
圖1　三臂機器人簡化幾何模型

1.1機器人空間坐標系的建立

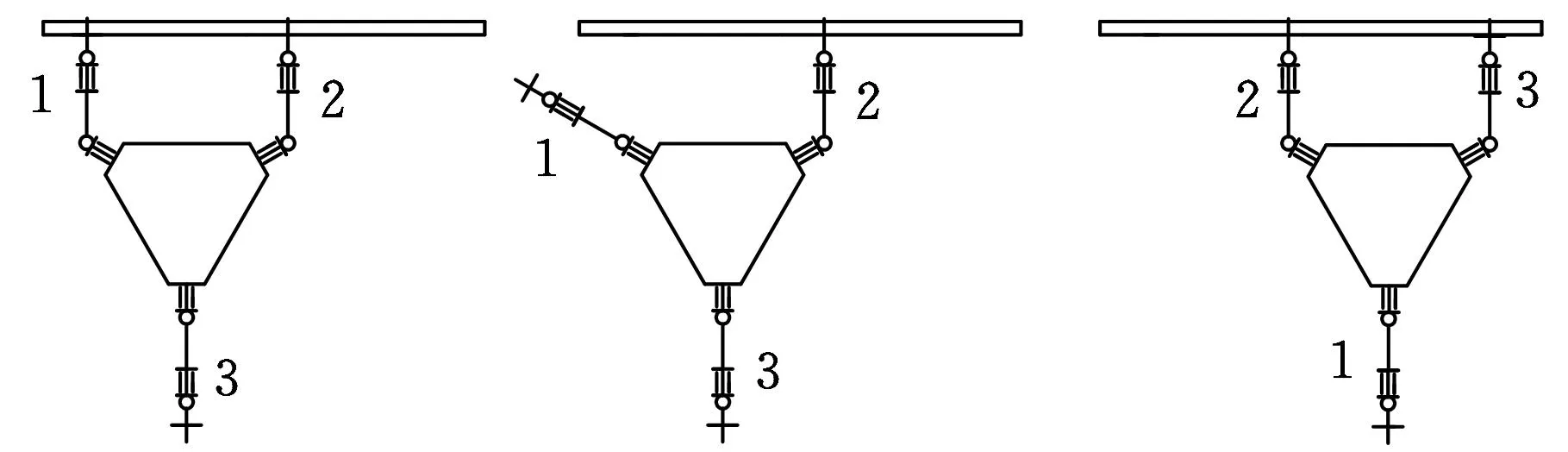
按照D-H方法建立機器人系統坐標系，如圖2所示。其中，OBXBYBZB是航天器的坐標系，OiXiYiZi是機器人各關節構件的動坐標系，機器人相鄰兩坐標系之間的矩陣用i-1T(i=1，2,…,n)表示，其中，i是機器人關節序號，前置序號i-1表示目的坐標系的序號，i-1=0表示機身坐標系。對于本文所設計的機器人，n=18。

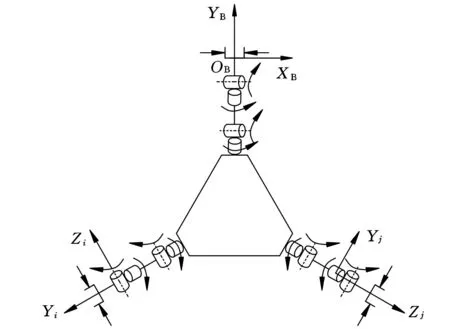
圖2　三臂機器人空間坐標系

1.2機器人運動學方程的建立

機器人是由一系列具有空間彎曲軸線的廣義連桿連接在一起構成的。根據三臂機器人的實際參數，可確定該模型的D-H參數，推導出三臂機器人的運動學方程方程[7-8]。記機器人的任意兩個關節序號分別為i和i-1，如圖3所示，固連在該2個關節上的動坐標系Z軸間的空間夾角(連桿扭角)為αi，空間最小距離(連桿長度)為bi，2個關節公垂線間的距離為di，2個關節X軸間的空間夾角(連桿夾角)為θi。

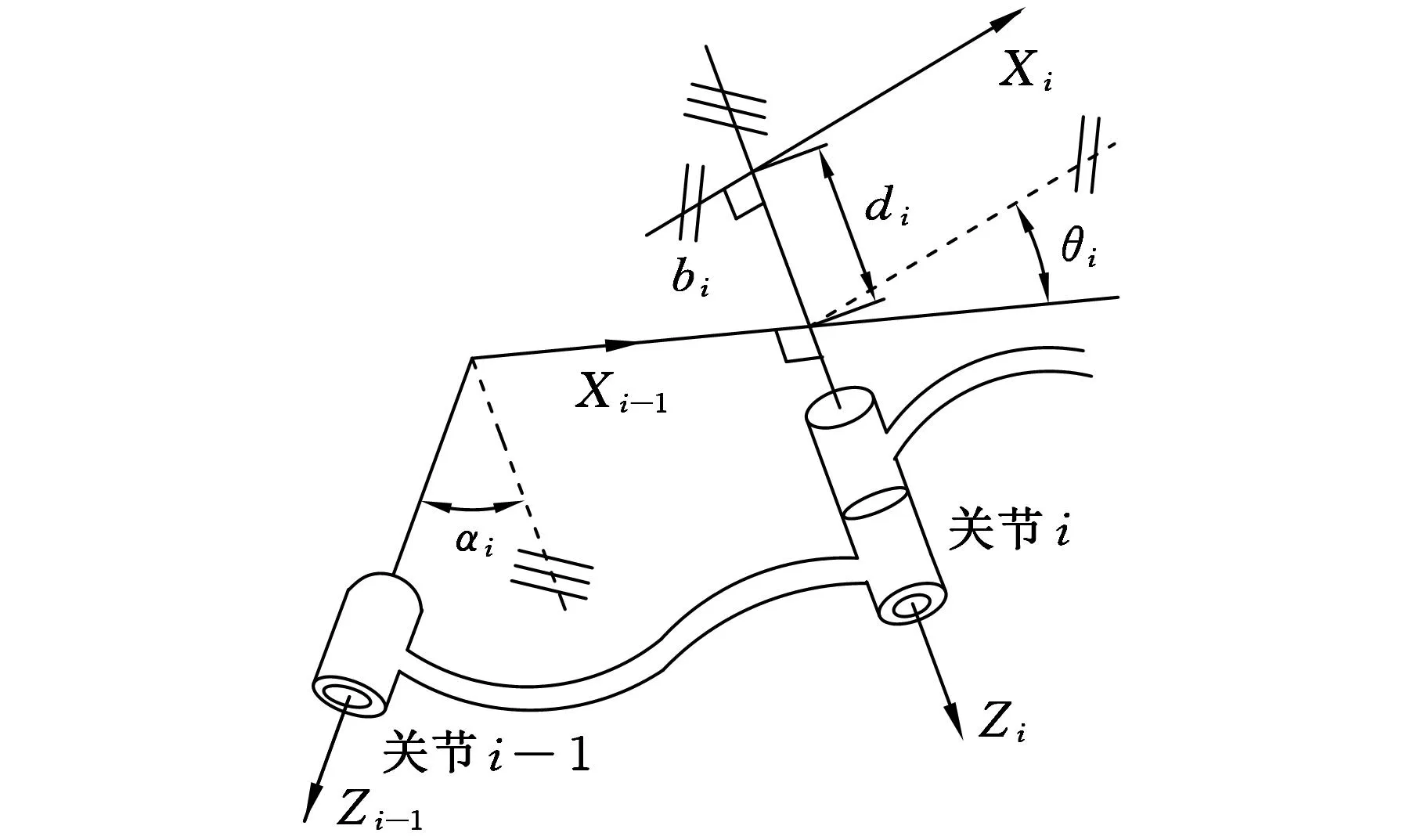
圖3　廣義連桿變換的4個特征參數D-H參數

上述D-H參數可通過如下兩次旋轉和兩次平移坐標變換從坐標系OiXiYiZi變換到坐標系Oi-1Xi-1Yi-1Zi-1[8-10]：①將坐標系OiXiYiZi繞Xi-1旋轉αi角，使Zi與Zi-1軸位于同一平面內；②將坐標系OiXiYiZi沿Xi-1軸平移bi，將坐標系OiXiYiZi原點移到Zi-1軸線上；③將坐標系OiXiYiZi繞Zi軸旋轉θi角，使Xi軸與Xi-1軸平行；④將坐標系OiXiYiZi沿Zi-1軸平移di。

上述坐標變換可用如下坐標變換矩陣i-1Ti描述：

(1)

因此推導出三臂機器人每條臂的坐標變化矩陣為

T=TBT11T2…5T6

(2)

則機械臂末端在航天器坐標系下的位姿坐標可表示為

P=TPB

(3)

式中，PB為航天器的位姿坐標。

2三臂機器人的仿真模型

2.1機器人的簡化幾何模型

在Pro/E軟件中建立三臂機器人的簡化模型，直接將裝配好的模型導入ADAMS軟件中進行仿真，其簡化模型如圖1所示。該模型僅包含實現機器人運動所必需的機械構件，其余附件及電機等未涉及，簡化模型的主要幾何參數如圖4所示。

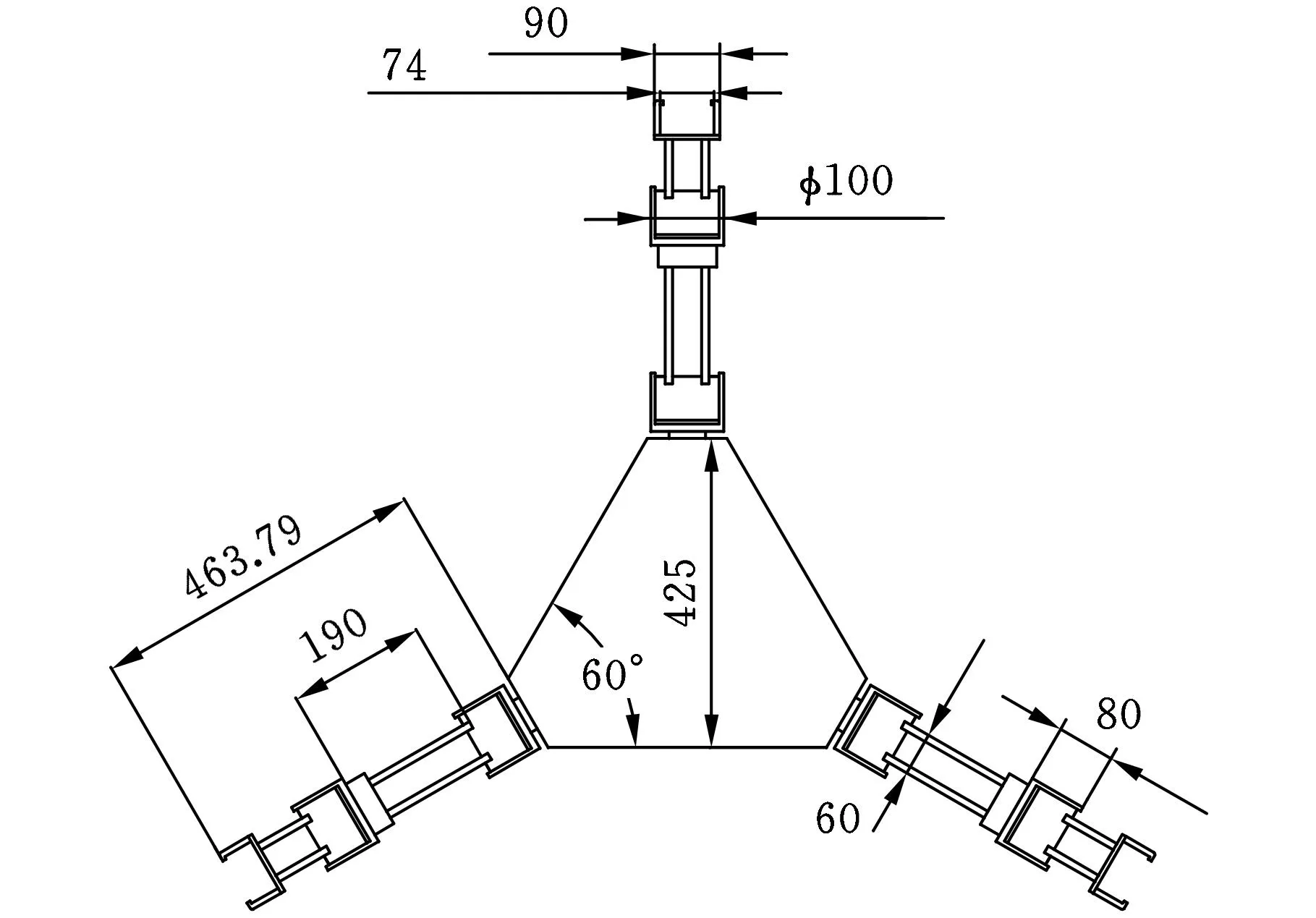
圖4　機器人簡化模型的主要幾何參數

2.2仿真模型建立

2.2.1模型質量設置

從Pro/E中導入的幾何模型是沒有質量的，在仿真前必須對各部件進行質量設置。本研究選用ADAMS軟件材料庫中的鈦合金，并在重力(Gravity)選項中將重力設置為無重力(模擬微重力狀態)或g/6(模擬月球環境重力)[11]，g為重力加速度。

2.2.2運動約束設置

在ADAMS/View環境中，模型構件之間的相互運動是靠運動副來實現的，在腰關節、大臂關節、腕關節和小臂關節之間添加旋轉副，在機械手添加移動副，其余構件添加固定副約束。

2.2.3接觸定義

當兩個構件表面間發生接觸并存在相對運動趨勢時，這兩個構件會在接觸區產生摩擦力，摩擦力隨接觸面正壓力的增大而增大，在ADAMS中稱為接觸力[12]。三臂機器人攀爬仿真過程中，當機械手抓住航天器上的桿狀扶手時，需要定義機械手與扶手之間的接觸。本研究選用IMPACT型接觸力和庫侖摩擦，其參數如表1所示。其中，材料剛度、阻尼和摩擦因數由材料性質所決定。

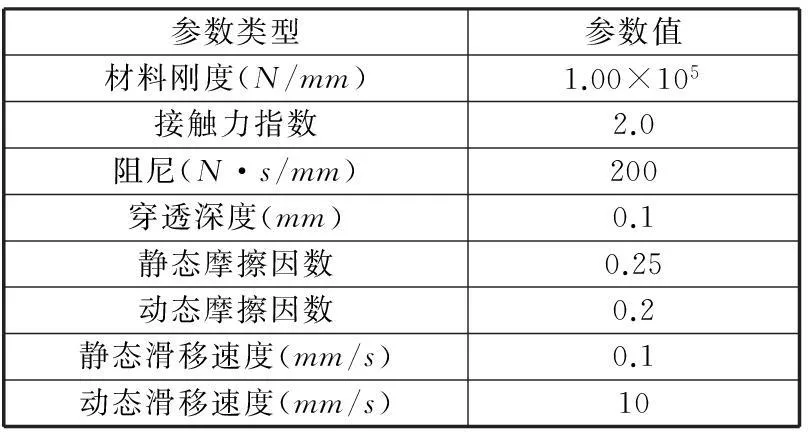
表1　仿真過程中接觸參數設置

2.2.4運動軌跡設計與驅動添加

對機器人模型施加驅動就是讓其未受約束的運動副按照某種規律變化。根據機器人的幾何結構特點，在仿真過程中只需要添加旋轉驅動與滑移驅動，將旋轉驅動添加到旋轉副和圓柱副，將滑移驅動添加到滑移副和圓柱副。每個運動副需要編寫獨立的驅動函數，以完成規定的運動軌跡。在本研究中，仿真運動軌跡規定為三臂輪流抓桿向前移動，起始動作為1號機械手抓桿，2號機械手開始運動抓桿；當2號機械手抓穩桿后，1號機械手脫離桿，同時3號機械手重復前述動作準備抓桿；如此往復，實現機器人沿攀爬桿向前運動。在整個攀爬過程中，機器人始終與YBOBZB平面平行，機械手的夾持力方向平行于XB軸。

本文仿真中實現上述運動的驅動函數采用step函數編寫。step函數是ADAMS函數庫中常用的函數，是三次多項式逼近階躍函數，由5個參數控制，分別為自變量(x)、自變量的初值(x0)和終值(x1)，函數值的初值(h0)和終值(h1)。在仿真中，從初值到終值的過程由軟件按照三次樣條擬合自動計算給出。step函數的具體格式為

step(x,x0,h0,x1,h1)

圖5為由step函數擬合得到的運動軌跡曲線[13]。本研究中采用時間位移驅動，即要求各關節在規定的時間內運動到規定的位置，自變量為時間坐標。圖6為爬桿過程步態圖。

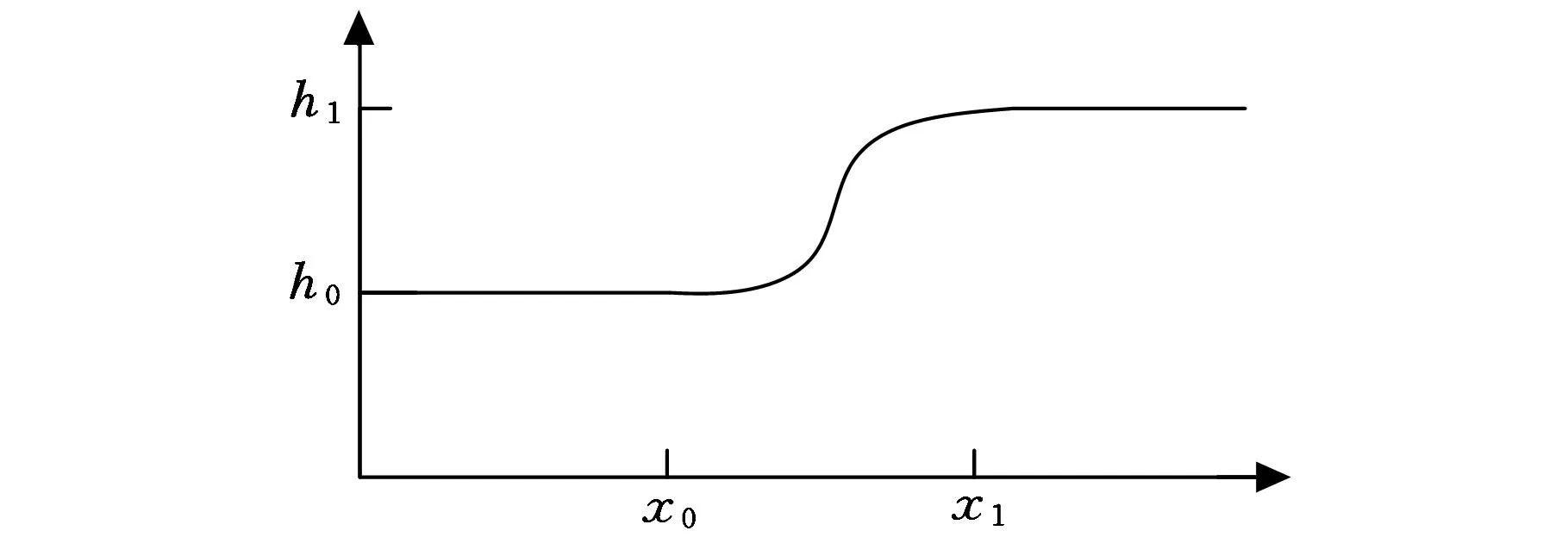
圖5　step函數擬合軌跡曲線

(a) (b)(c)

(d) (e)(f)圖6　機器人仿真步態示意圖

基于上述驅動函數，設計運動過程如下：

(1)初始位置設為1號手臂抓桿前的位置，3條手臂伸直與機身位于同一平面內，即XBOBYB平面，1號手臂平行于YB軸，其余兩條手臂與之成120°，桿置于1號機械手內，見圖6a。

(2)1號手臂的兩只機械手沿桿軸線方向運動(XB向)閉合抓桿，見圖6b，運動時間0.1s。

(3)除1號手臂外，其余部件繞1號手臂腰關節旋轉90°，機器人在YBOBZB平面內運動，運動時間1 s，見圖6c。

(4)2、3號手臂和機身繞1號手臂大臂關節在YBOBZB平面內旋轉60°，然后，2號手臂繞其大臂關節再旋轉60°，2號手臂到達抓桿前狀態，運動時間共計4s，見圖6d。

(5)2號手臂的兩只機械手閉合抓桿，其運動時間為1s；1、2號手臂同時抓桿時間持續1s。

(6)1號手臂的兩只機械手向桿的反方向運動，松開爬桿，運動時間1s。

(7)1號手臂繞其大臂關節旋轉-60°，1、3號手臂和機身繞2號大臂關節在YBOBZB平面內旋轉-120°，3號手臂繞其大臂旋轉60°，3號機械手到達抓桿前位置，見圖6e和圖6f。

(8)3號手臂的兩只機械手閉合抓桿，其運動時間和驅動函數同過程(2)中設置，兩只手同時抓桿時間持續1s。

(9)重復上述過程，實現機器人的整個攀爬過程。

不失一般性，本文僅對1號手臂抓兩次桿，2、3號手臂各抓一次桿進行仿真。1號機械手驅動函數為

step(time,0,0,0.1,-17.2)+step(time,9,0,10,17.2)+

step(time,31,0,33,-17.2)

其余驅動函數在此不再列出。為減小同時動作帶來的振動影響和前一次動作對后一次動作的影響，在編制驅動函數時，所有運動副的動作時間不重疊。

3仿真結果及分析

本文在無重力和不同方向g/6重力環境下分別對三臂機器人的爬桿過程進行動力學仿真，獲得不同環境下機械手受力情況和大臂關節運動過程扭矩曲線，為機器人的設計提供參考。

3.1機械手受力情況分析

圖7～圖9分別為三臂機器人在無重力、g/6重力環境下3條手臂的機械手受力曲線，其中，CONTACT_1.FX為1號手臂的機械手夾持力(XB向)曲線，CONTACT_5.FX為2號手臂的機械手夾持力(XB向)曲線，CONTACT_8.FX為3號手臂的機械手夾持力(XB向)曲線。重心位于機器人幾何中心。

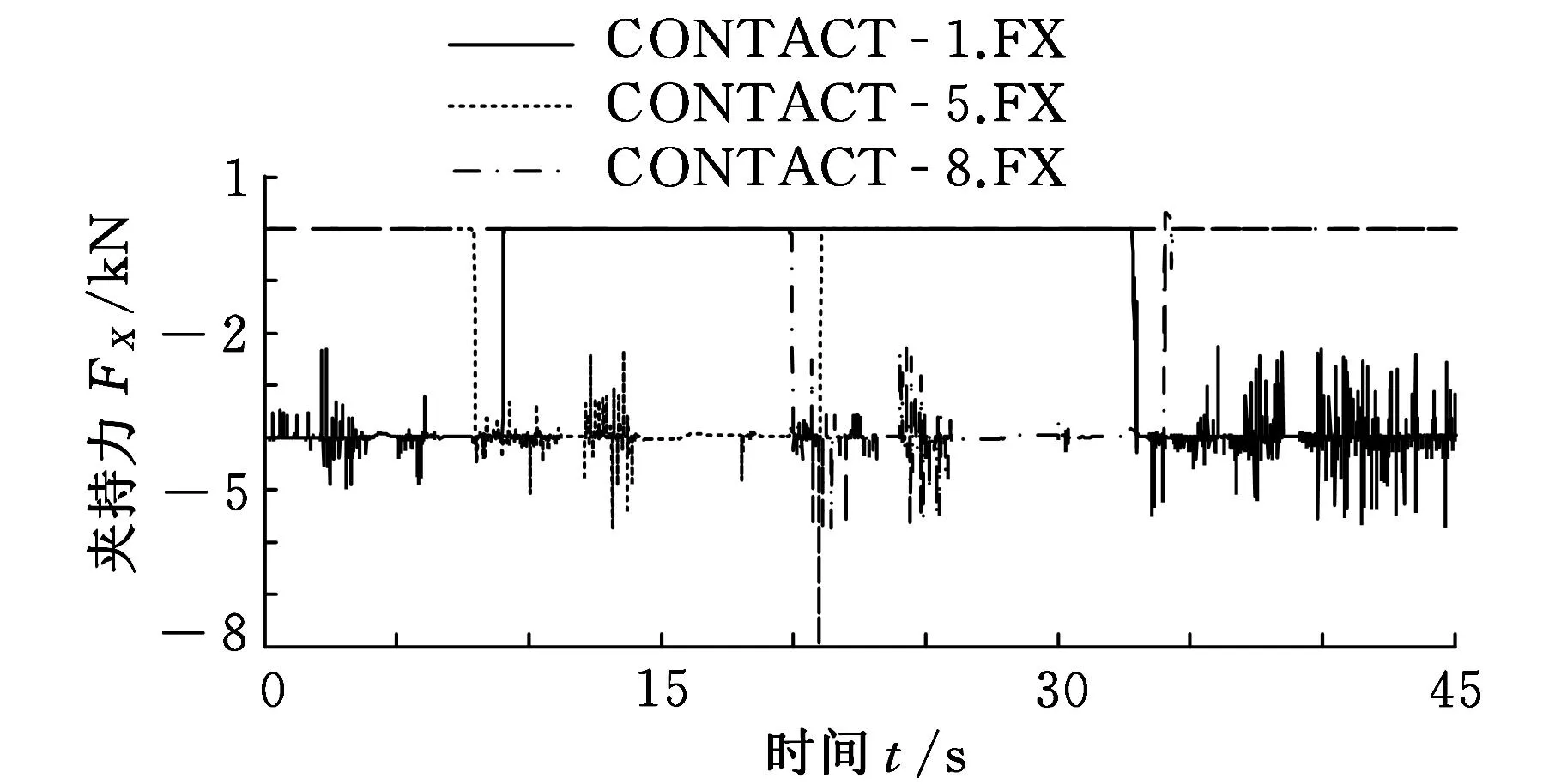
圖7　無重力環境下3條手臂機械手受力情況

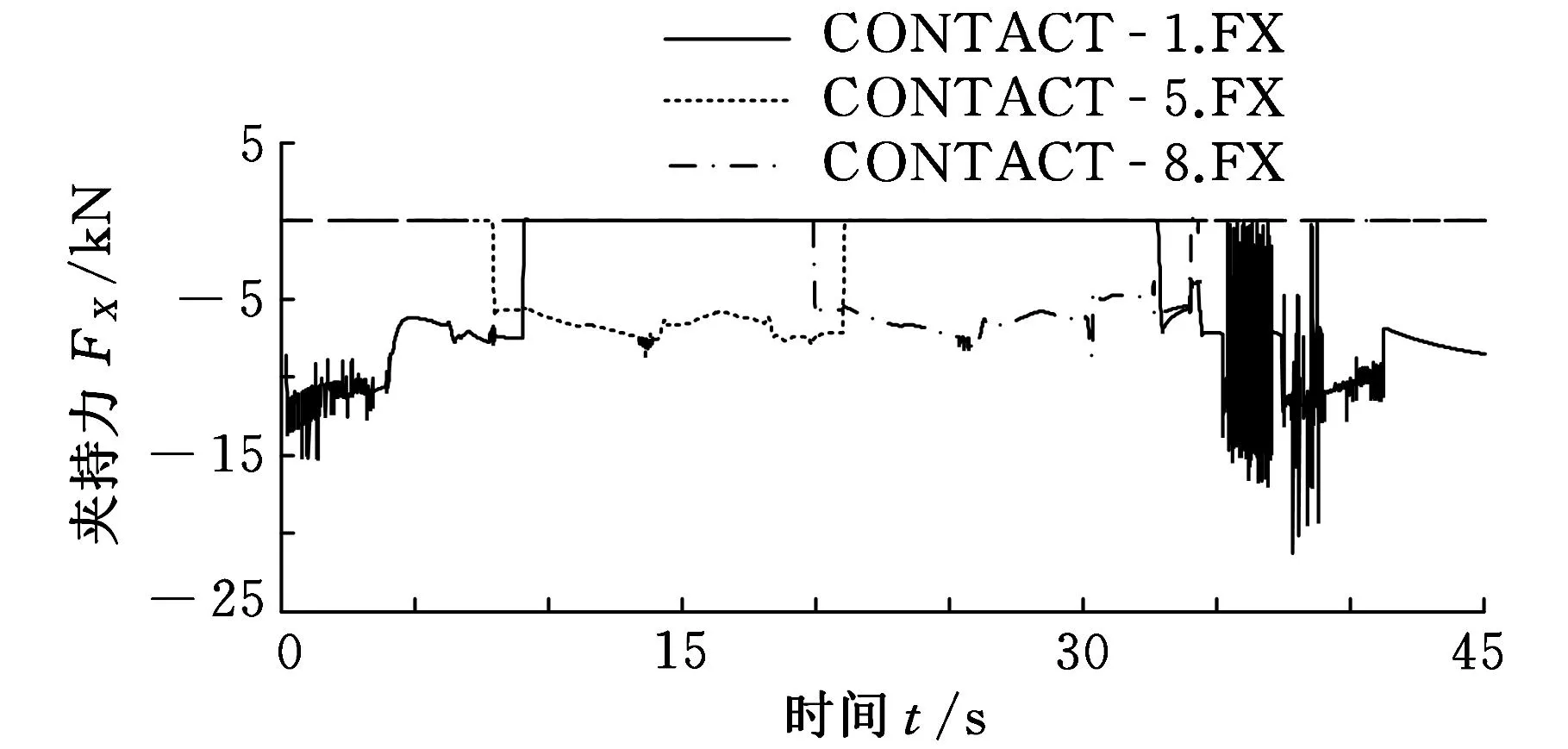
圖8　重力平行于XB軸環境下3條手臂機械手受力情況

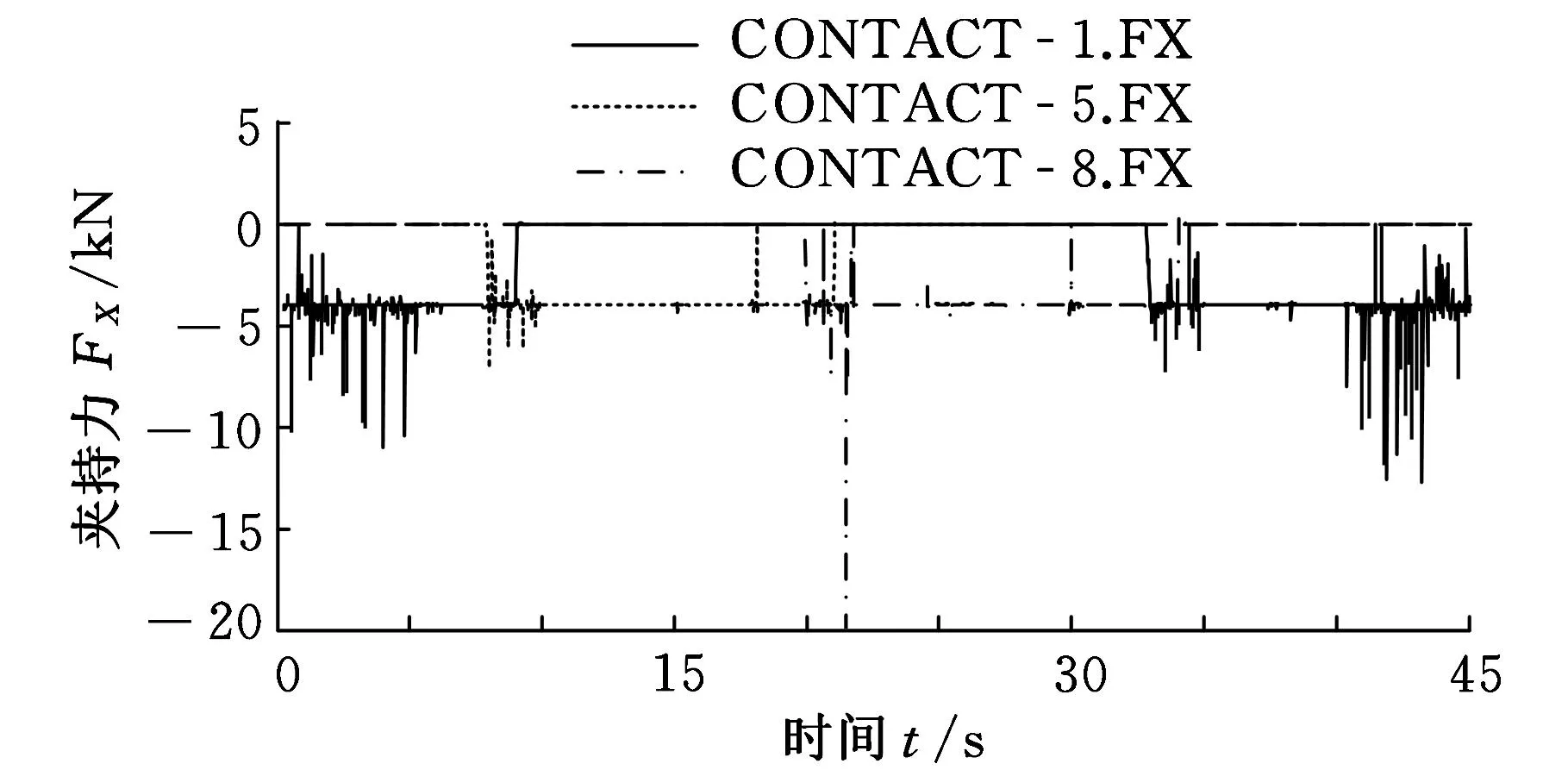
圖9　重力平行于-YB軸環境下3條手臂機械手受力情況

由上述仿真結果可見，雖然1號手臂首次抓桿持續時間遠遠短于其他兩條手臂和1號手臂第二次抓桿持續時間，但3條手臂的機械手在抓桿過程中受力基本一致。由此可知，抓桿過程的速度變化基本不影響夾持力的大小。在整個爬桿過程中，機體運動會引起機械手與桿之間的相對運動，如圖10所示。圖10a所示為理論抓桿狀態，機械手兩側手掌和軌道與桿的3個平面完全接觸，在所允許的切入深度下緊握爬桿，但實際中會出現圖10b～圖10d所示的情況。圖10b兩側手掌切入深度不一致(左側大于右側)，圖10c和圖10d接觸面變為部分接觸，這種接觸方式之間的變換導致接觸力發生波動。

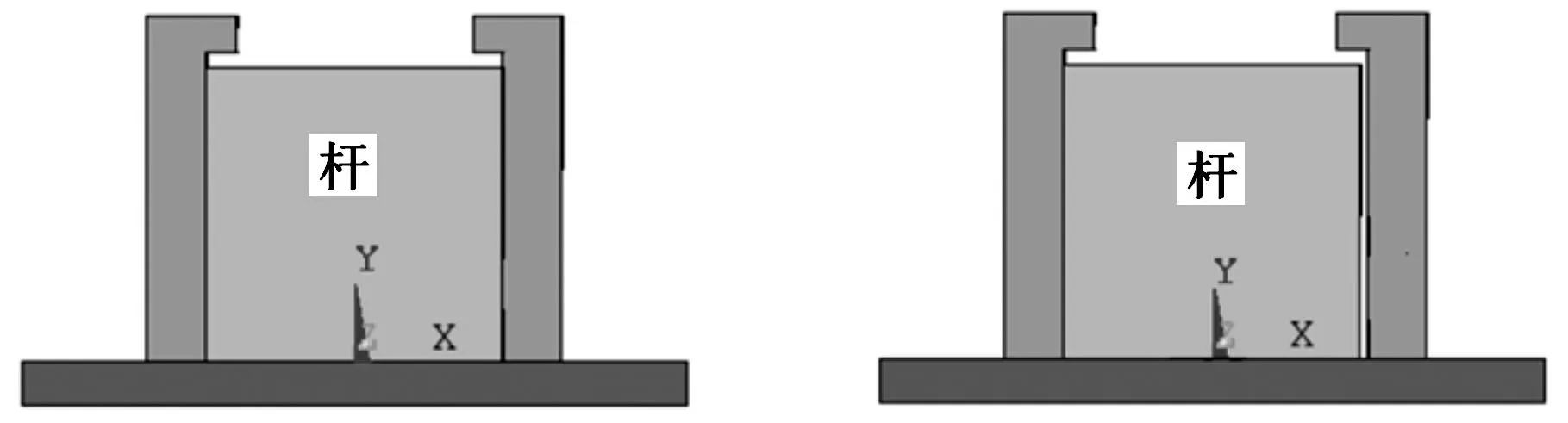
(a)(b)

(c)(d)圖10　機械手抓桿接觸狀態

例如，2～3s時，1號機械手抓緊爬桿，機身繞YB軸旋轉，轉動過程對機械手的受力影響較大，造成夾持力發生波動，如圖11所示。一側手掌夾持力增大的同時另一側手掌夾持力減小，為防止機械手脫離爬桿，控制兩側手掌的接觸力在某一數值(如-4000N)上下波動。圖11中2條曲線分別為1號機械手在無重力情況下兩只手掌的夾持力曲線，夾持力峰值最大達到-5700N，波動幅度與平均夾持力相比增大30%。11～17s時1號手臂脫離爬桿,3號手臂向抓桿位置擺動，夾持力峰值在12～14s期間波動較大,達到-5785N，如圖12所示。機體轉動慣性會使機體發生晃動，嚴重的晃動不僅造成夾持力波動，若控制不當甚至會使機械手滑落爬桿，因此，應進一步考察機身轉動速度對夾持力的影響情況。

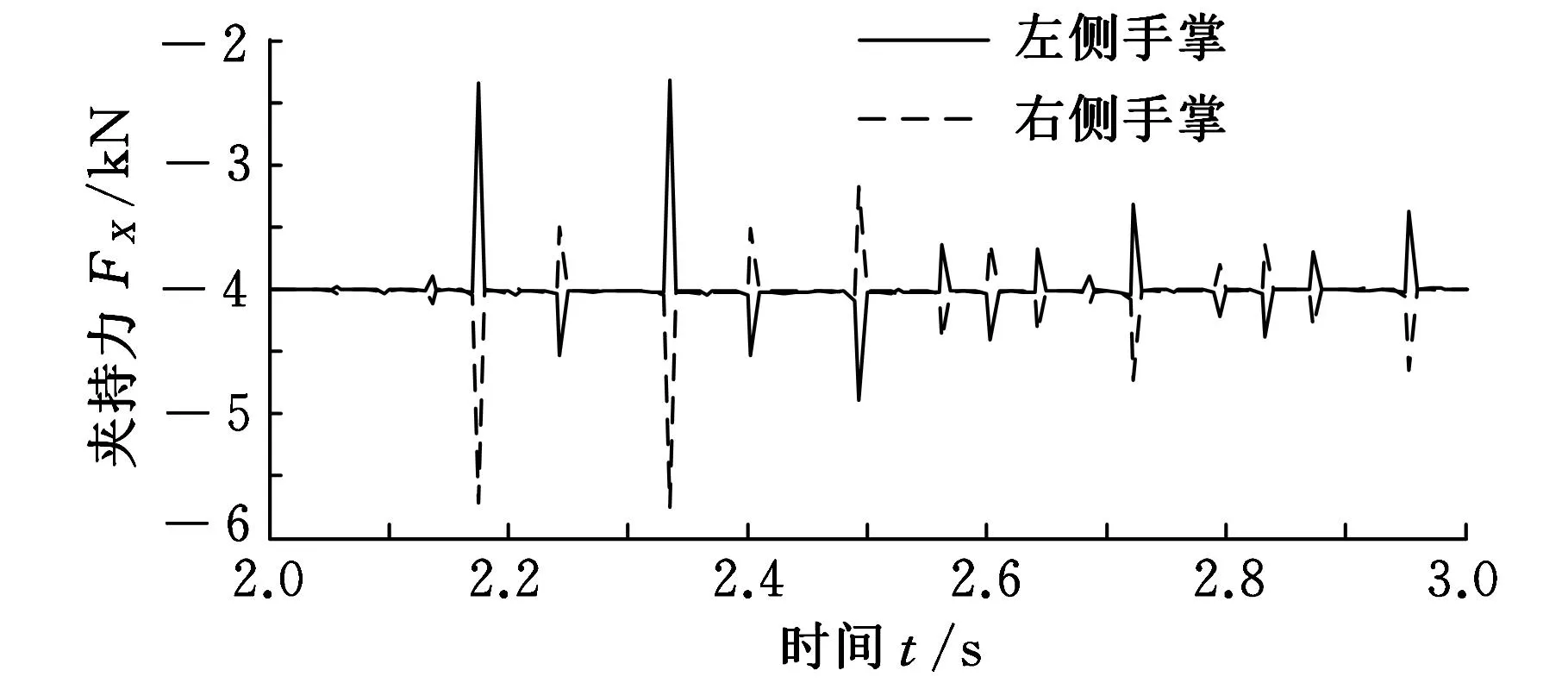
圖11　無重力情況下1號機械手夾持力

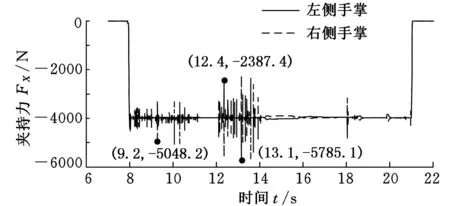
圖12　無重力情況下2號機械手夾持力

圖13所示為三種重力情況下2號機械手夾持力曲線對比，圖中曲線1為無重力情況下仿真結果，曲線2和3分別為重力方向為XB向和-YB向的仿真結果。值得指出的是，重力對夾持力有較大影響。當重力方向與夾持力方向一致(即重力方向為XB向)時，重力在造成夾持力增大的同時，還會使得兩只機械手夾持力不相等，在快速抓桿時出現多次碰撞(圖10)，導致抓桿困難。當重力方向與夾持力方向垂直(即重力方向為-YB向)時，重力使得夾持力波動幅度和頻率減小。以上情況表明，無重力狀態的運動姿態較重力場中的運動姿態更難控制。

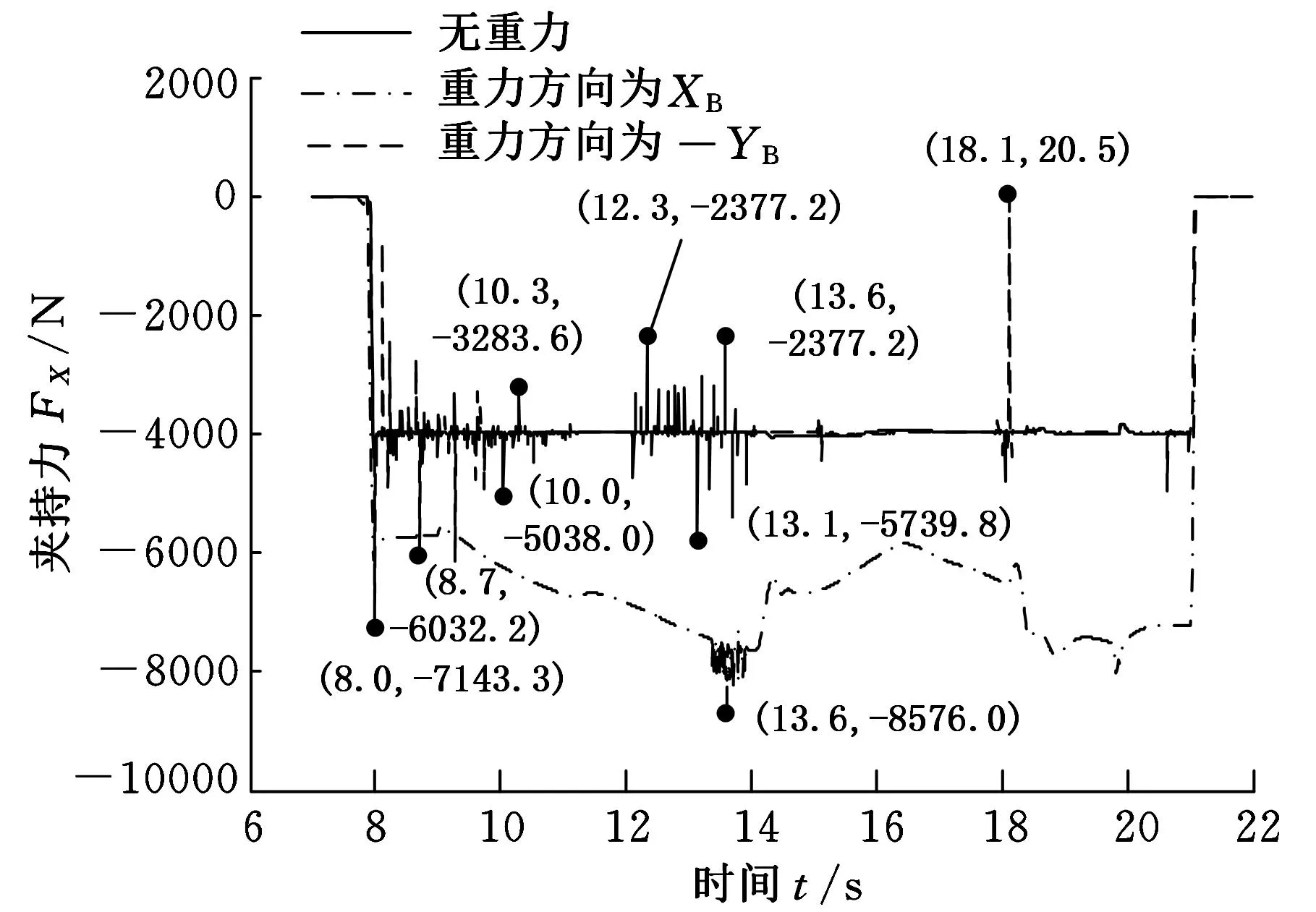
圖13　三種重力情況下2號機械手夾持力

3.2機械手軌道受力情況分析

對于上述設計步態，在機械手與爬桿接觸之前，機械手軌道的一端首先與桿發生碰撞，此后逐漸碰撞到達指定部位(圖14中從右至左)。此時軌道平面與桿平面接觸或平行，該過程會給大臂關節形成沖擊，造成大臂關節逆向轉動。如果驅動力矩不夠大，則機械手將無法到達抓桿前指定位置。圖15～圖17為三種環境下軌道的受力情況，其中CONTACT_6.FY為1號機械手軌道的受力曲線，CONTACT_3.FY為2號機械手軌道的受力曲線(-YB向)，CONTACT_9.FY為3號機械手軌道的受力曲線，2號機械手軌道方向與其他二只機械手軌道的坐標方向相反。

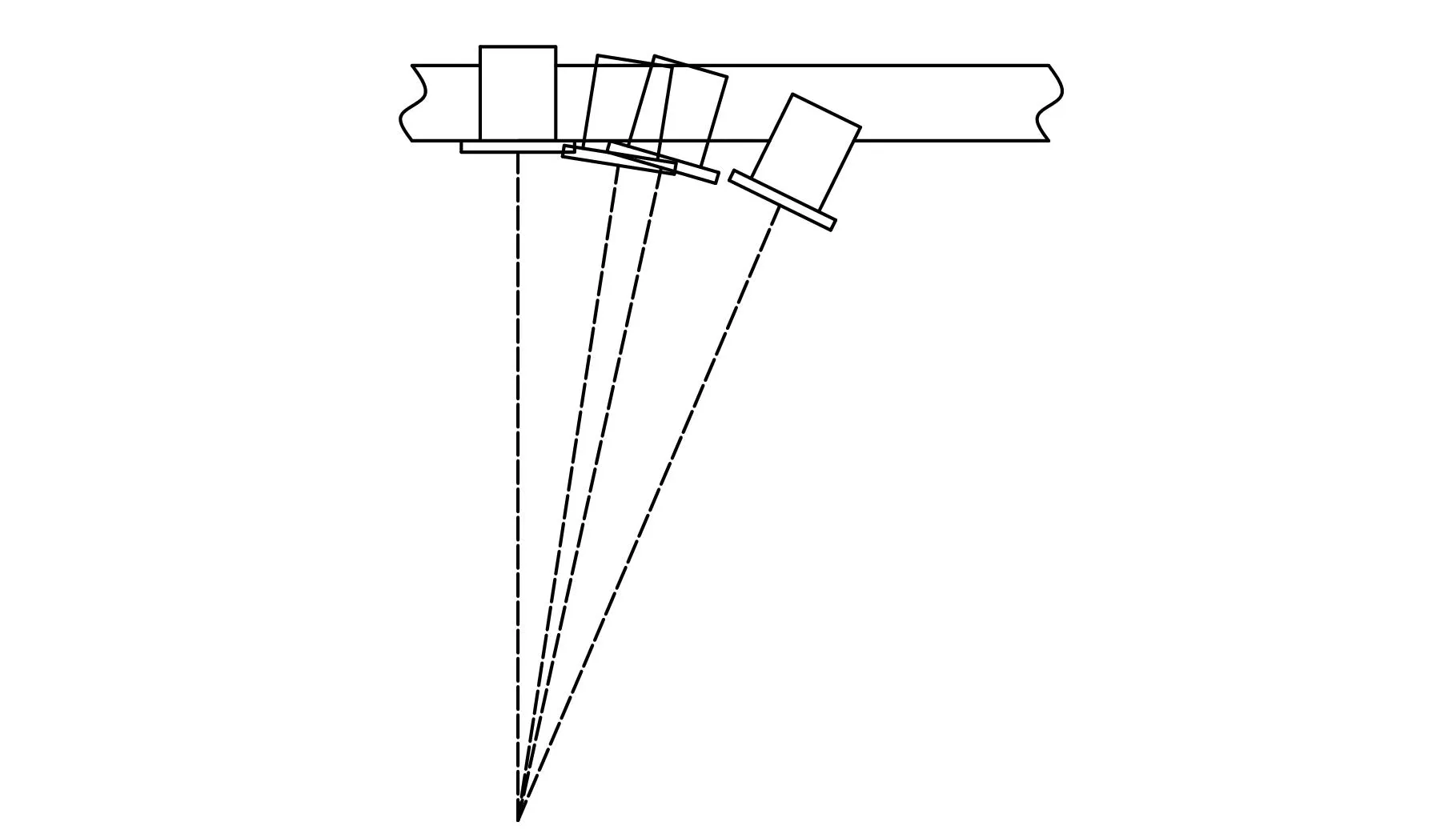
圖14　機械手軌道與桿碰撞過程

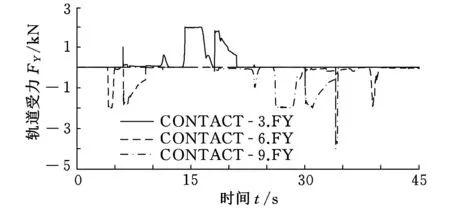
圖15　無重力環境下3條手臂機械手軌道受力情況

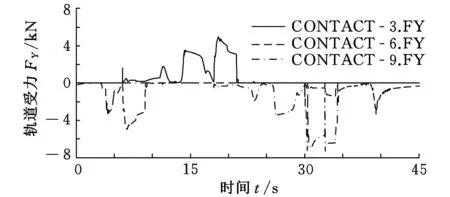
圖16　重力平行于XB軸環境下3條手臂機械手軌道受力情況

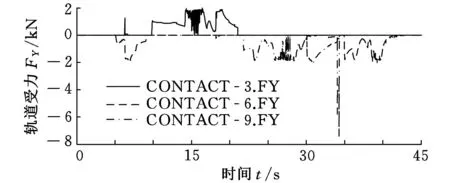
圖17　重力平行于-YB軸環境下3條手臂機械手軌道受力情況

由上述曲線看出，在機械手抓緊爬桿后手掌和桿接觸面之間的相對運動比較頻繁，導致軌道接觸力頻繁波動。從碰撞力來看，重力平行于XB軸環境下碰撞力最大。表2為各種環境下機械手及其軌道最大受力匯總表。

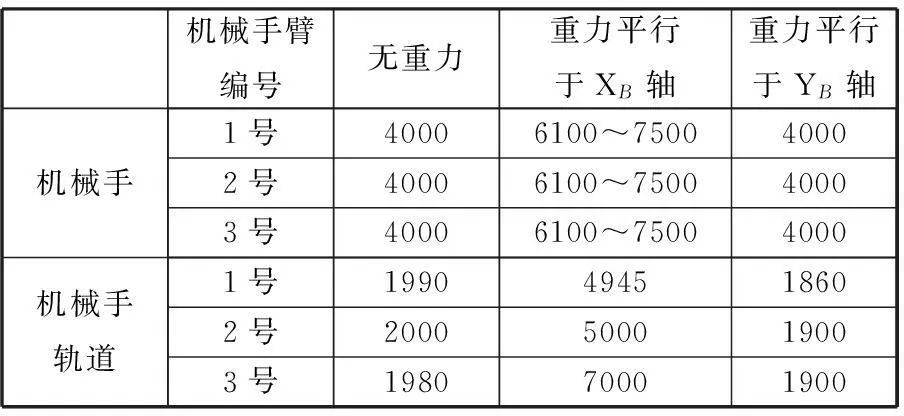
表2　三種環境下機械手受力　N

4結論

(1)對于本文設計的步態，為了驗證抓桿速度和多關節同步運動對機械手夾持力的影響，對1號機械手和2、3號機械手分別采用不同抓桿速度進行仿真分析，結果表明，抓桿速度對夾持力的影響不明顯。在腰部回轉時采用多關節聯動、其他關節單獨運動的方式進行仿真分析，結果表明，多關節聯動會造成機器人振動加劇，夾持力增大，夾持力波動加大，故在設計機器人控制策略時應盡量避免多關節聯動。

(2)重力對機器人的姿態影響較大，在設計重力環境下機器人攀爬路線時，應盡量讓重力和夾持力與桿長度方向垂直(重力為-YB向)，這樣可使姿態容易保持穩定。

(3)應改進設計機械手軌道，盡量減少其邊緣對桿的碰撞；同時改變關節運動順序，將邊緣首先碰撞改為整個軌道平面與桿全接觸，這樣可減小碰撞力引起的機器人振動。

(4)在仿真過程中，仿真參數設置對仿真結果影響較大，本文所設置的參數主要以經驗值為依據，仿真結果可為這類空間機器人的設計與控制提供定性參考。

參考文獻：

[1]RastegariR,MoosavianSAA.MultipleImpedanceControlofSpaceFree-flyingRobotsviaVirtualLinkages[J].ActaAstronautica, 2010, 66:748-759.

[2]梁捷, 陳力. 雙臂空間機器人基于高斯型函數的姿態、關節運動模糊自適應補償控制[J]. 中國機械工程, 2010, 21(3):330-336.

LiangJie,ChenLi.FuzzyAdaptiveCompensationControlforSpace-basedRobotSystemwithDual-armBasedonGaussian-typeFunctiontoTrackTrajectoryinJointSpace[J].ChinaMechanicalEngineering, 2010, 21(3):330-336.

[3]慧記莊, 魏芳勝, 高凱，等. 基于ADAMS的冗余驅動并聯機器人動力學仿真研究[J]. 工程設計學報, 2012,19(5): 362-365.

HuiJizhuang,WeiFangsheng,GaoKai,etal.StudyonDynamicsSimulationofRedundantlyActuatedParallelRobotBasedonADAMS[J].ChineseJournalofEngineeringDesign, 2012,19(5): 362-365.

[4]孫漢旭, 賈慶軒, 張秋豪, 等. 基于三分支機器人關節空間軌跡規劃的研究[J]. 北京郵電大學學報, 2006, 29(3):81-85.

SunHanxu,JiaQingxuan,ZhangQiuhao,etal.TrajectoryPlanninginJointSpaceBasedonTri-BranchRobot[J].JournalofBeijingUniversityofPostsandTelecommunications, 2006, 29(3):81-85.

[5]孫漢旭，姬羅栓，徐揚生. 空間三臂機器人在操作中的平衡問題[J]. 北京郵電大學學報, 2002,25(1):34-38.

SunHanxu,JiLuoshuang,XuYangsheng.StudyofBalanceProblemforaThree-armSpaceRobotduringItsManipulation[J].JournalofBeijingUniversityofPostsandTelecommunications, 2002, 25(1):34-38.

[6]葉平, 孫漢旭. 具有冗余度的三分支空間機器人逆運動學分析[J]. 機械工程學報, 2005, 41(11):58-62.

YePing,SunHanxu.AnalysisofInverseKinematicsforThree-branchSpaceRobotwithRedundancy[J].ChineseJournalofMechanicalEngineering, 2005, 41(11):58-62.

[7]SugaTG,KumarV.ControlofCooperatingMobileManipulators[J].IEEETransactiononRoboticsandAutomation, 2002, 18(1)：94-103.

[8]方琛瑋. 基于ADAMS機器人動力學仿真研究[D]. 北京：北京郵電大學，2009.

[9]ZhuangYF,LiuDQ,WangJG.DynamicModelingandAnalyzingofaWalkingRobot[J].TheJournalofChinaUniversitiesofPostsandTelecommunications, 2014, 21(1):122-128.

[10]甘屹, 王均壘, 孫福佳. 基于給定工作空間的6R型機器人D-H參數優化設計[J]. 中國機械工程, 2014, 25(22):3003-3007,3011.

GangYi,WangJunlei,SunFujia.OptimalDesignofD-HParametersofa6RRobotforaPrescribedWorkspace[J].ChinaMechanicalEngineering, 2014, 25(22):3003-3007,3011.

[11]姬廣勛. 履帶式載人月球車移動系統的設計與運動性能分析[D]. 哈爾濱：哈爾濱工業大學, 2013.

[12]SharfI,ZhangYN.AContactForceSolutionforNon-collidingContactDynamicsSimulation[J].MultibodySystemDynamics, 2006, 16(3):263-290.

[13]阮鵬, 俞志偉, 張昊, 等.基于ADAMS的仿壁虎機器人步態規劃及仿真[J]. 機器人，2010, 32(4):499-509.

RuanPeng,YuZhiwei,ZhangHao,etal.GaitPlanningandSimulationofGeckoInspiredRobotBasedonADAMS[J].Robot, 2010, 32(4):499-509.

(編輯蘇衛國)

Dynamic Simulation for a Three-arm Robot on Orbit

Huang Jinying1,2Du Weimin3Li Hui1Jiang Zhihong1Yang Huan2

1.Beijing Institute of Tecnology,Beijing,100081 2.North University of China,Taiyuan,030051 3.Henan Branch of Air Traffic Control of Civil Aviation of China,Zhengzhou,451162

Abstract:A simplified robot model with three arms was designed according to the needs of space operations. The coordinate transformation matrix was established based on the D-H method and the kinematic equations of the robot were derived. Based on ADAMS virtual prototyping technology, the climbing process of the robot on a pole was simulated for three kinds of gravity, respectively. The force curves and effect factors were obtained so as to offer the design references for the robot.

Key words:robot; on orbit; simulation; clamping force

收稿日期：2014-08-15修回日期：2015-12-07

中圖分類號：TP241.2

DOI：10.3969/j.issn.1004-132X.2016.03.008

作者簡介：黃晉英, 女, 1971年生。北京理工大學宇航學院博士后研究人員，中北大學機械與動力工程學院教授。主要研究方向為動力學分析與控制。杜為民，女，1966年生。中國民用航空河南空管分局高級工程師。李輝，男，1982年生。北京理工大學機電學院講師。蔣志宏，男，1974年生。北京理工大學機電學院副教授。楊歡，男，1988年生。中北大學機械與動力工程學院碩士研究生。