門座式起重機臂架及自重平衡系統的優化設計研究

曹 娜

(天津港第五港埠有限公司 天津300456)

門座式起重機臂架及自重平衡系統的優化設計研究

曹 娜

(天津港第五港埠有限公司 天津300456)

隨著經濟的發展和國際物流業的繁榮，港口物流對門座式起重機裝卸貨物的效率、使用的安全可靠性等工作性能提出了更高的要求。因此，對門座式起重機各方面的研究一直是國內外的熱點。四連桿鉸接組合臂架變幅系統是目前應用較廣泛的門座式起重機臂架形式。優秀的變幅系統設計以盡可能降低變幅機構的驅動功率和提高機構的操作性能為目的，臂架系統自重平衡的設計優劣是影響門及整體工作性能、安全性能的重要因素。

臂架系統自重平衡 Matlab 優化設計 UG Ansys

0 引 言

天津港第五港埠有限公司(以下簡稱“公司”)有4臺門機在滿載作業時均存在著不同程度的拉桿、沖桿現象，不能達到最大工作幅度。拉桿、沖桿，指的是起重機在進行變幅運動時臂架不能在變幅范圍內平穩進行變幅運動，在變幅過程中的某點產生很大的沖擊載荷，使臂架系統不能繼續伸展。這會帶來以下問題：①起重機在這種情況下按照原有變幅行程作業極有可能發生變幅齒條的損壞，乃至更嚴重的門機傾覆事故。②門機作業不能達到額定變幅，造成門機抓取范圍縮小，需要大量機械輔助作業，加大作業成本。

本文以40～43,m門座式起重機為研究對象，對其進行臂架系統設計方案和理性分析，并以其結構尺寸為依據建立門座式起重機臂架系統的優化數學模型。利用Matlab優化工具箱對其進行優化求解，并根據優化結果設計可行的改造方案，然后利用UG軟件對改造后的臂架系統進行三維建模，利用ANSYS軟件對其關鍵部位進行靜力學強度校核，以驗證優化的效果。

1 門機臂架系統四連桿機構合理性分析

1.1 設計目標

40～43,m門機采用的臂架形式是四連桿組合形式，該形式的臂架系統設計目標為：①四連桿各部位長度合理，使吊重(貨物)在變幅過程中運行軌跡趨近于平行于水平面的直線；②門機變幅時由貨物產生的變幅阻力盡量小；③臂架系統各桿件、平衡系統以及貨物對臂架下鉸點產生力矩的矢量和盡量小，且在變幅過程中的某個位置達到力矩的平衡；④平衡重盡量小。

驗證臂架四連桿機構設計的合理性首先要建立該系統的簡化模型，列出各部位參數相互制約的關系式，驗證四連桿機構的運動軌跡是否符合預期。

1.2 簡化模型

門機四連桿組合臂架系統可以簡化為如圖1所示的以點O、O’、A、B為頂點的四連桿模型，而點A、B、C組成的三角形剛性梁結構即為象鼻梁的簡化形式，臂架四連桿機構的桿件尺寸的設計合理性首先要驗證象鼻梁端點在變幅行程內的運動軌跡，也就是C點的軌跡是否接近一條水平直線。

圖1 臂架系統四連桿簡化模型Fig.1 Simplified model of luffing system’s four-bar linkage

1.3 象鼻梁端點軌跡計算

為了方便計算，首先將臂架四連桿相關的尺寸參數用字母表示，如圖2所示：

圖2 臂架四連桿Fig.2 Luffing system’s four-bar linkage

另外，令θ1=∠ABC ；θ2=∠AOA′；θ3=∠ACC′；θ4=∠EOA ；θ5=∠O1OE；θ6=∠O1AB ；θ7=∠EAO；θ8=∠O1AE ；θ9=∠OAA′；θ10=∠CAA′。

則在最大幅度時有：

將兩式分別平方并求和得：

展開并整理得：

解此一元二次方程可得最大幅度時主臂架擺角：

同理可求得最小幅度時主臂架擺角：

以主臂架擺角θ2作為自變量，θ2min到θ2max是其變化范圍，則有：

利用MATLAB軟件的繪圖功能可以繪制出點C(Xc，Yc)的曲線。編寫程序需要的相關數值根據幾何關系可計算如下：

帶入已知40～43,m門機的臂架系統參數，在Matlab中編寫繪圖函數M文件(部分)如下：得到C點軌跡圖如圖3。

圖3 象鼻梁端點運動軌跡Fig.3 The trajectory of Trunk beam end point

由圖3可以看出，Yc在整個變幅過程中雖然變化值不是很大，但在接近最大變幅時曲線上揚有一個明顯拐點，這很可能就是臂架變幅在接近最大時發生失穩的重要原因。

1.4 臂架失穩原因的確定

為進一步確定臂架在變幅過程中失穩的原因，我們采用力矩檢測工具對門機變幅過程中變幅系統減速器高速軸的力矩進行了測量，得到結果如表1所示：

表1 變幅系統減速器高速軸扭矩測量結果Tab.1 Torque measurement results of high speed shaft of reducer

在門機變幅系統的設計中，臂架進行變幅運動時應存在一個力矩平衡點，即力矩零點，而由表1可以看出在整個變幅過程中減速器高速軸的扭矩方向始終沒有變化(數值始終為負)，因此在變幅過程中不存在扭矩為零的變幅平衡點。這一點導致了門機臂架進行變幅的過程中穩定性不佳，進而不能達到最大幅度的結果。

2 門機臂架及平衡系統優化數學模型的建立

門機臂架及平衡系統的優化數學模型包括3個要素，即：設計變量、目標函數和約束條件。

2.1 設計變量的確定

以上文建立的臂架四連桿簡化模型為基礎，添加上平衡系統的相關參數，即構成了臂架及平衡系統的整體簡化模型(見圖4)。

圖4 門機臂架平衡系統優化設計變量Fig.4Designed variables of crane boom balance system optimization

如圖4所示，由于點O和O1位置固定，則l9，l10，l11的長度固定，l5的值一般也取為常量，這里不做改變，需要優化的參數包括：

l1——主臂架的長度；l2——象鼻梁后臂長度；l3——大拉桿長度；l4——象鼻梁前臂長度；l6——象鼻梁鉸點與小拉桿下鉸點距離；l7——主臂架下鉸點到小拉桿下鉸點距離；l12——小拉桿長度；l13——平衡梁前臂長度；l14——平衡梁后臂長度；l15——配重中心點到小拉桿上鉸點距離；Gp——配重重量。

這其中l14平衡梁后臂長度由于受到機房位置尺寸的影響不宜變動，因此也不做變化。

由此就得到了臂架及平衡系統的10個設計變量，用向量表示為：

根據經驗值，設定設計變量上限：

lb＝[30；4；24；10；20；5；6；1；6；45,000]；

設定變量上限為：

Ub＝[40，8；35；20；30；10；12；5；13；55,000]。

2.2 目標函數的確定

2.2.1 象鼻梁端點運動軌跡

根據1.3的具體運算，得到象鼻梁端點坐標函數方程：

在xc在最大幅度與最小幅度之間變化時，yc應該接近于yc=H的一條直線，則目標函數可表示為：

2.2.2 變幅阻力矩

臂架的變幅阻力矩可以利用象鼻梁端點C軌跡表達式并根據功能原理進行計算。設臂架從位置一擺動到位置二時臂架與水平面夾角θ2角變化值為Δθ2，象鼻梁端點C軌跡的高度變化為Δyc，負載貨物重量為Q。則C點為取得克服貨物重力升高Δyc所需的能量，需在臂架上作用力矩ΔM，且有：

ΔM×Δθ2=Q ×Δyc

由此得：

因此當臂架擺角幅度足夠小時，每相鄰兩個幅度位置的象鼻梁端點高度差值為單位重量貨物所引起的在該微量擺角行程上的臂架力矩。

2.2.3 臂架平衡系統不平衡力矩

若將臂架平衡系統中各桿件設為均質等截面桿件，則平衡系統重量可表示為：

式中：1η為主臂架長度重量，2η為象鼻梁長度重量，3η為大拉桿長度重量，4η為平衡系統長度重量。

對于本文引用的40～43,m門機，其長度重量計算如表2。

表2 臂架平衡系統長度重量計算Tab.2 Boom balance system length weight calculation

定義了長度重量后，整個臂架平衡系統則完全簡化為有長度、有重量，無寬度、無高度的桿件系統模型。由于在變幅過程中主臂架下鉸點O為臂架系統的回轉中心，根據瞬心回轉功率法，可以計算各桿件自重對O點的力矩。

對重應與臂架重力、象鼻梁重力，以及拉桿重力的一半(如不計杠桿系統自重重力)相平衡。

2.2.3.1 象鼻梁自重力矩Mxbl

由于整個象鼻梁長度和為l2+l4，而長度重量的定義把所有桿件設為均質桿件，則重心位置應位于處，即BC上位于B點處。

則象鼻梁對主臂架下鉸點O的力矩為：

式中：Gxbl=η2(l2+l4)——象鼻梁自重(kg)。

2.2.3.2 大拉桿自重力矩Mdlg

設大拉桿自重的一半Gdlg作用在 F 點，則：

2.2.3.3 主臂架自重力矩Mzbj

式中：Gzbj=η1l1——主臂架自重(kg)。

2.2.3.4 平衡系統自重力矩Mph

設平衡重系統(包括配重、平衡梁、小拉桿)的合成中心在P點，則：

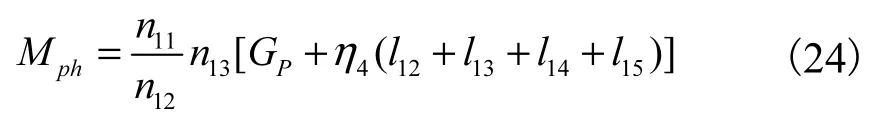
式中：GP——平衡重重量。

2.2.3.5 系統不平衡力矩

臂架系統自重力矩為主臂架、象鼻梁、大拉桿及變幅齒條自重力矩之和，即：

整個臂架及平衡系統的不平衡力矩為臂架系統力矩與平衡系統力矩之差，即為：

2.2.4 配重重量

在滿足平衡條件的情況下，配重的重量應該取盡量小的值，因此：

f3(X)＝Gp(目標函數3)

其中，Gp為配重重量。

2.3 約束條件的確定

在臂架平衡系統的設計中，約束限制主要包括結構布局方面的限制、設計準則要求限制、經驗數據限定的變量范圍等方面，約束條件的限定既可以避免計算過程中可能發生的超界溢出現象，又可以提高優化搜索速度，在優化設計的過程中具有相當重要的作用。本文根據以下幾個方面制定優化約束條件：

2.3.1 象鼻梁前后臂的長度比

象鼻梁的前后臂的比值根據起重機設計手冊為：象鼻梁前臂長度為后臂的0.3～0.5倍，即：

這里可表現為兩個約束關系式：

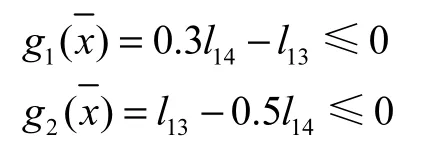
2.3.2 臂架與水平面夾角

臂架于水平面的夾角根據經驗數據其變化范圍在30～80 °之間，即：

這里也需要兩個約束表達式：

2.3.3 象鼻梁與水平線夾角

象鼻梁同水平線之間的夾角變動范圍在8～90,°之間，即：

用約束表達式可以表達為：

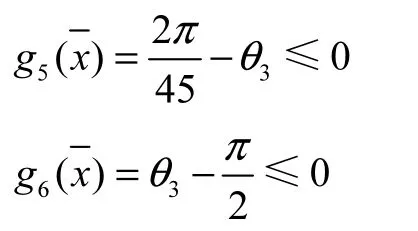
2.3.4 臂架系統四連桿機構約束

即：

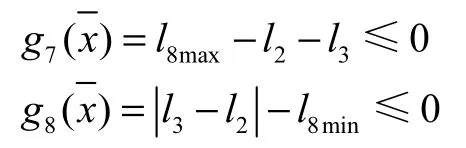
2.3.5 平衡系統四連桿機構約束

2.3.6 鉸點E的設計

即：

2.3.7 平衡量前后臂夾角

由于平衡梁后臂應該設計得盡量長，所以平衡梁前后臂夾角應為鈍角，設平衡量前后臂夾角為θ11，即有：

還有，應要求臂架處于最小幅度時，平衡重不與機房碰撞。設平衡梁后臂與豎直線夾角為θ12，即：

2.3.8 臂架不平衡力矩

在最大、最小幅度時，臂架系統的不平衡力矩應有利于臂架恢復正常位置。若設載荷對主臂下鉸點O 引起的力矩有使臂架系統向大幅度方向運動的趨勢為正，有向小幅度方向運動的趨勢為負，則在最大幅度時，臂架系統不平衡力矩應為負，在最小幅度時，臂架系統不平衡力矩應為正，則有約束：

式中：mwphmax、mwphmin分別為載荷在最大幅度，最小幅度時的桿件自重不平衡力矩。

此外，根據起重機設計手冊，臂架平衡系統不平衡力矩應小于臂架四連桿對O點力矩之和的十分之一，則有：

寫成約束函數則為：

3 臂架及平衡系統的優化

3.1 目標函數f文件的編寫

根據上文對優化目標的定義，一共有3個目標函數，將目標函數f文件命名為BJPH_3,mb_MB．m，編寫程序如下(部分)：

function f＝BJPH_3,mb_MB(x)

Smin＝8.76；Smax＝39.743；H＝16.87；l5＝0.854；l9＝14.4；l10＝5；l14＝0.6；已知條件定義(最小、最大幅值；起升高度；象鼻梁鉸點偏移距離；主臂架下鉸點與大拉桿下鉸點水平、豎直距離；象鼻梁后臂距離)。

a1＝x(1).^2＋Smax.^2＋H.^2－x(4).^2；

a2＝2.*x(1).*Smax；

a3＝2.*x(1).*H；

……

f(1)＝abs(yc－H)；%,目標函數1

f(2)＝Mbj－Mph；%,目標函數2

f(3)＝x(10)；%,目標函數3

3.2 約束條件M文件的編寫

根據上文對約束條件的定義，將目標函數M文件命名為BJPH_3,mb_YS．m，編寫程序如下(部分)：function[g，ceq]＝BJPH_3,mb_YS(x)

l14＝0.6；%,已知條件象鼻梁后臂長度

Smin＝12；Smax＝48；H＝16.87；L5＝0.854；

l9＝14.4；L10＝5；

a1＝x(1).^2＋Smax.^2＋H.^2-x(4).^2；

……

g(16)＝Mbjmax-Mphmax；

g(17)＝Mphmin-Mbjmin；

g(18)＝Mbj-Mph-0.1.*Mbj；

ceq＝[]；

3.3 優化函數的調用及優化結果

調用優化工具箱的fgoalattain函數需要首先進入MATLAB軟件主頁面，開啟優化工具箱后在彈出的優化工具箱界面中選擇優化函數以及設定基本參數，優化結果顯示(部分)：

x＝1.0,e＋04 *

0.003 ,4－0.000,0,i

0.000 ,6＋0.000,0,i

0.002 ,8

……

0.000 ,9

0.000 ,3

0.000 ,8

5.300 ,0＋0.000,0,i

fval＝

1.0 ,e＋04 *

0 0 5.300,0＋0.000,0,i

根據MATLAB計算結果，40～43,m門座式起重機優化前后相關參數變化如表3。

表3 優化參數比較表Tab.3 Comparison of optimization parameters

4 優化后模型的三維建模及靜力分析

4.1 三維模型建立

根據優化設計結果，在調整主臂架、象鼻梁前后臂、大拉桿及小拉桿的長度后，在UG中建模如圖5～9。

圖5 主臂架三維模型Fig.5 3D model of the main arm

圖6 象鼻梁三維模型Fig.6 3D model of the Trunk beam

圖7 大拉桿三維模型Fig.7 3D model of the big draw rod

圖8 小拉桿三維模型Fig.8 3D model of the small draw rod

圖9 平衡梁三維模型Fig.9 3D model of the balance beam

根據各桿件在各自鉸點上相連接的相互約束的條件，將主臂架、象鼻梁、大拉桿進行裝配，并設計一部件代替門機機身主體，將其設為固定桿件，則主臂架可以繞主臂架下鉸點和大拉桿下鉸點作變幅運動。臂架系統裝配模型如圖10。

圖10 臂架系統裝配模型Fig.10 3D model of the arm rack system assembly

4.2 平衡系統的ANSYS有限元分析

將UG中建立的平衡梁三維模型導入ANSYS，在ANSYS中進行參數設置以及網格劃分。

模型的工程單位、單元類型和材料性質設置如下：

工程單位，長度，mm；

質量，kg；

重量，N；

單元類型，二節點的三維梁單元；

圖11 平衡梁及小拉桿有限元模型Fig.11 Finite element modle of balance beam and small draw rod

材料性質，楊氏彈性模量 E＝2.06,e＋5,MPa；

泊松比μ＝0.3；

建立完成的平衡梁有限元模型如圖11所示。

4.2.1 主要載荷

由結構自重引起的載荷SG。

4.2.2 靜力計算結果

下面分別給出結構增加活配重前后平衡梁、小拉桿應力計算結果表4所示：

表4 1類工況應力計算結果Tab.4Stress calculation results of Category 1 working conditions

由表4可以看出，小拉桿結構應力增加15.921,MPa，平衡梁結構應力增加20.132,MPa，其所受應力云圖見圖12、13。

圖12 平衡梁應力云圖Fig.12 Stress cloud of balance beam

圖13 小拉桿應力云圖Fig.13 Stress cloud of small draw rod

4.2.3 彈性極限評估

在結構中，所用到的材料為Q235C，其機械性能如下：

彈性極限 σE＝235,MPa

1、2、3類工況的許用應力σα如下：

1類工況σα1＝σE/1.5＝156.7,MPa

2類工況σα2＝σE/1.33＝176.7,MPa

綜上所述，該平衡系統在優化之后結構仍滿足靜力強度的要求。

5 平衡系統改造

根據表3比價系統桿件長度變化量相對于初始長度變化幅度很小，而配重重量變化幅度較大，可見該門機逼架平衡系統的主要問題在于配重不足。考慮到臂架系統改造難度大、成本高，最終決定僅對平衡系統進行改造。其方案是：增加的后配重為兩個圓柱形箱體，焊接于原配重兩側，以增加配重重量。改造后的優點為：①提高門機的抓取范圍，減少下艙機械的輔助作業時間，降低作業成本；②變幅系統整體載荷狀況改善，降低了便服系統故障頻次級門及維修成本。■

［1］ 劉劍波. 單臂架門座式起重機臂架變幅系統的優化設計[D]. 上海：上海交通大學，2011.

［2］ 孫翔. 門座式起重機臂架四連桿結構設計[J]. 工程技術：引文版，2016(5)：248.

［3］ 黃陳娣. 淺析門座式起重機臂架系統的優化設計[J].科技促進發展，2012(5)：128-130.

Optimized Study of Portal Crane’s Boom and Dead Load Blanced System

CAO Na
(Tianjin Port No.5 Stevedoring Co.，Ltd.，Tianjin 300456，China)

Along with the development of economy and the prosperity of international logistics industry，efficiency，safety and reliability of port logistics portal crane regarding loading and unloading of goods are facing higher requirements．Therefore，research on various aspects of portal crane has become a hot topic both at home and abroad．Luffing system of four connecting rod hinge arm is the most widely used form of portal crane jib．The portal crane is used to change the amplitude of the agency．The design of the luffing system to reduce the driving power of luffing mechanism and improve the operating performance of institutions is an important factor affecting the performance of the door and the whole work and safety performance.

self balance arm frame system；Metlab；optimization design；UG；Ansys

TH21

：A

：1006-8945(2016)10-0062-08

2016-09-02