中期電力負荷預測及負荷模型的研究

郭平創

（廣東電網有限責任公司湛江吳川供電局，吳川 524500）

?

中期電力負荷預測及負荷模型的研究

郭平創

（廣東電網有限責任公司湛江吳川供電局，吳川 524500）

摘 要：本文以中期電力負荷預測及負荷模型的研究為題展開論述。首先分析了負荷時間的序列樣本，并對時代段的變動趨勢進行了預測。在此基礎上，建立了中期負荷模型。最后，結合相關的實例，對中期負荷進行測試。實踐證明，采用中期電力負荷預測方法，可以實現電力系統的優化調度。

關鍵詞：中期 電力負荷 預測 模型 研究

為了保證電力系統的正常運行，需要對電力負荷進行預測，并及時優化系統調度計劃。對電力負荷進行預測時，要求以歷史樣本序列為標準，同時建立合適的數據模型，以此來推斷用戶的用電需求與最大負荷。通常情況下，主要采用綜合用電水平法、用電單耗法以及時間序列法等預測用電量。本文結合相關文獻資料，按照時間序列法建立數學模型，對歷史資料預測點的性質進行分析。

1 預測模型與預測方法

本文在中期電力負荷預測研究中，負荷的時間范圍設置為一個月。同時，對用戶每天24小時產生的負荷進行預測。在具體的時間序列內，中期電力負荷呈現出上升、下降或者保持不變的特點。另外，中期電力負荷在特定的年份、季度中呈現出的變動趨勢，應該與其在某一時段中的變化趨勢一致［1］。

1.1 負荷時間序列樣本分析與時間段變動趨勢預測

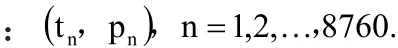
在分析時間序列樣本時，要求以歷史資料為標準，對平年、閏年，月份，周進行分解。同時，標示出每周工作日、休息日以及節假日。然后，研究電力負荷變動的規律。比如，以上述樣本 （tn，pn）為例，找出對應的負荷值。然后，建立新的時間序列。這些序列由上面被提取出來的時間組成。假設k代表工作日，i代表休息時間，j代表節假日。那么，每個月的儲存方式為：

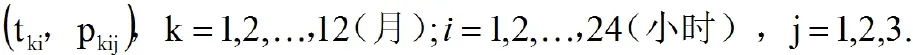
然后，根據以上的儲存方式，再利用最小二乘法分析。假設yi為每天預測的負荷值，ti為時間。那么，二者之間的關系可以用下面的多項式來表達。

式（1）中，C1代表工作日的回歸系數，C2代表休息日的回歸系數，C3代表節假日的回顧系數。這幾個數據是預測電力負荷的基礎。然后，根據時間序列計算出每月、每季度以及每天的修正系數。通過這些修正系數可以看出序列的增長率。最后，結合誤差分析方法、最小二乘法，得出每個時間段負荷變動的平均值［2］。負荷時間序列樣本以及趨勢預測流程圖如圖1所示。

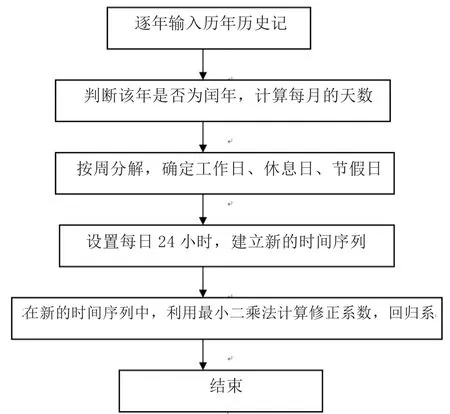
圖1 負荷時間序列樣本分析及趨勢預測流程圖

1.2 中期負荷預測

第一，按照以上辦法，確定出每月工作日、休息日以及節假日24h的基礎負荷曲線。第二，根據每年電力負荷的增長速度，對各個時間段的趨勢進行修正，得出最終的中期負荷曲線。第三，以中期優化調度為標準，重新排列出三種曲線的順序，然后制定對應的持續負荷曲線。

2 中期負荷模型的研究

2.1 趨勢外推法

趨勢外推法指的是季節波動比較小，電力負荷隨著時間變化呈現出一種上升、變化的趨勢。根據這種變化的特點，用函數曲線來反映。假設t代表時間，y為因變量，可以得到模型：y =f （t）。如果這種趨勢不斷向前發展，只要帶入t值，就能夠計算出時間序列的未來值。該模型在應用過程中具有數據少、計算方便的優點。但是，由于電力負荷存在一定波動，很容易產生誤差，具有很大的缺陷［3］。

2.2 彈性系數法

彈性系數法是國內生產總值與電量平均增長率的比值。根據彈性系數以及當前國內的用電生產總值，可以對未來的用電總量進行規劃。因此，彈性系數法與國民經濟發展的速度和用戶的總用電量有很大關系。彈性系數法具有計算簡單、操作方便的優勢。缺點是，應用前，需要做大量的調研工作。

2.3 灰色模型法

在應用過程中，灰色模型法主要是對不確定性因素進行統計。通常情況下，以某個階段的規律為依據，建立負荷預測模型：一種是灰色模型，一種是最優化灰色模型。灰色模型在短期負荷預測中應用較多。該預測模型的優點是：需要考慮數值的變化，對負荷數據要求低，同時計算方便、精度結果高。缺點是：如果數據離散程度增高，就會導致數據灰度增加，從而產生很大誤差。另外，該模型不適合電力系統長后期預測。

2.4 回歸分析法

回歸分析法指的是以過去負荷歷史資料為依據，建立數學分析的數學模型。利用回歸分析法，可以根據統計學方面的原理，對觀測到的數據進行分析，然后預測出未來電力負荷的發展趨勢。該模型分為一元線性回歸、多元線性回歸和非線性回歸。在中期電力負荷預測中，經常使用線性回歸分析法。優點為：預測結果精準，比較適用于中、短期預測。缺點是：統計總產值的難度比較大［4］。此外，運用回歸分析法，只能預測電力負荷發展的綜合水平，沒有辦法對各供電區的負荷發展水平進行預算。

雖然通過以上辦法可以得出新序列的持續負荷曲線，但是該負荷曲線并不是中期優化調度的最終負荷模型。在電力系統優化調度中，傳統的辦法為建立二階梯模型。但是，這種模型在反映系統功率或者水電廠收益中經常出現誤差。尤其在谷差較大的情況下，很容易產生較大的功率缺額。因此，該建模方式存在很大的局限性。針對以上問題，當前在電力系統優化調度中，主要采用多階梯數學模型。通過對電網每日的持續負荷與峰谷差進行分析，建立四階梯模型比較實際。該建模不但操作簡單，而且可以達到很高的精準度。同時，在不同階梯的時間段內，它能夠自由選擇持續負荷曲線。

圖2為二階梯建模下，形成的負荷虛線。其中，實線代表每日持續負荷，虛線代表二階梯下，計算出來的近似負荷。在電氣負荷較大的情況下，采用二級階梯建模方式往往會產生較大的功率缺額，因此不利于電力負荷的優化調度。與二階梯建模不同，采用四階梯對電力系統進行優化調度，不會出現以上情況。可以說，四階梯在電力系統優化調度中發揮著重要的作用。如圖3所示。

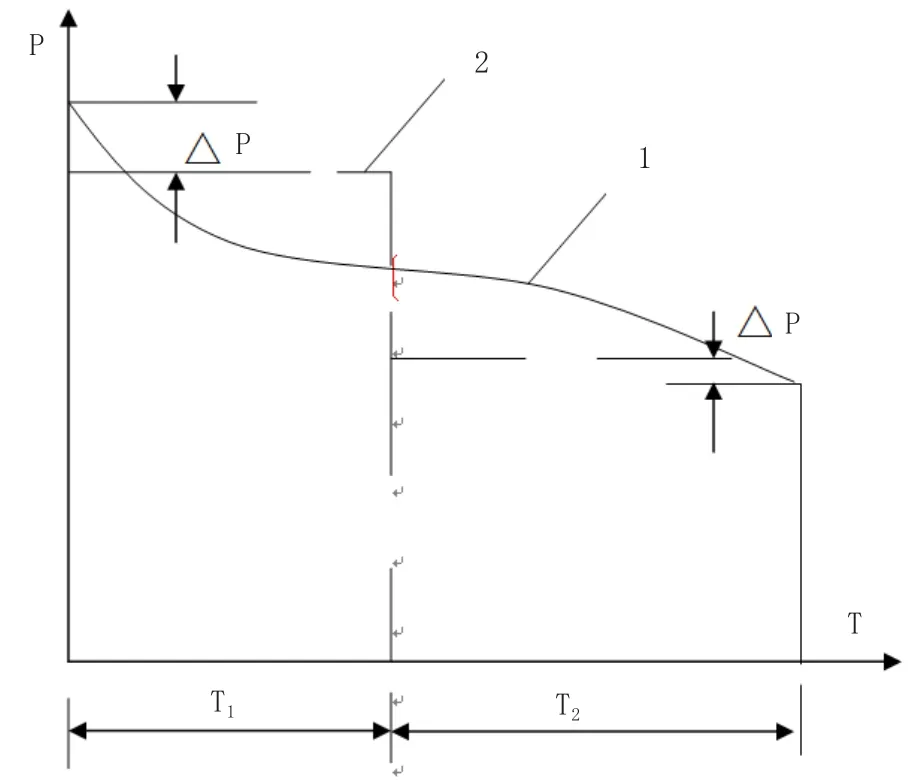
圖2 二階梯模型

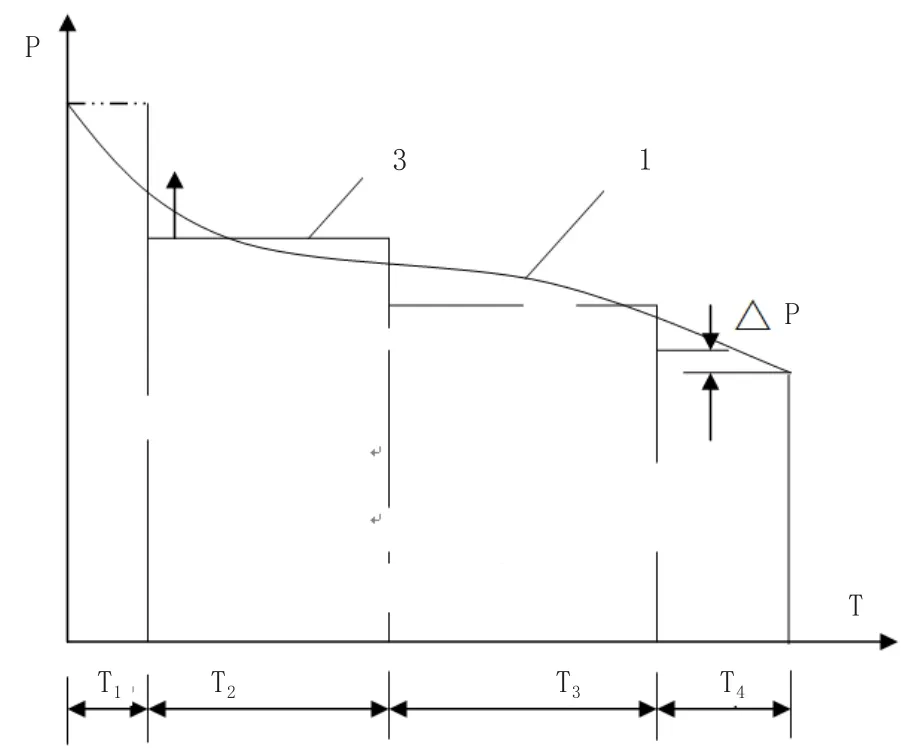
圖3 四階梯模型

四階梯負荷模型在使用過程中，要求峰荷、日發電量以及谷荷處于相對穩定的狀態，不能隨意發生改變。計算公式為：

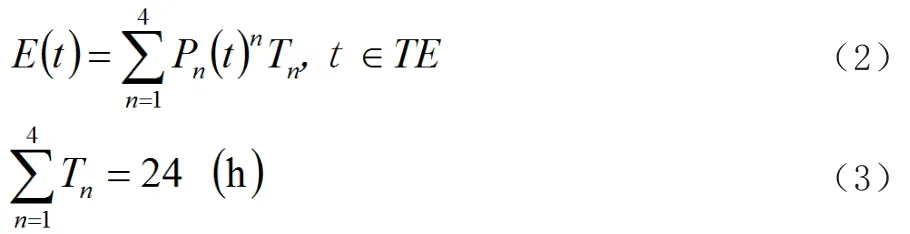
式（2）中，E（t）代表每日負荷電量。TE代表調度周期中，每個時段的指標集。Tn代表在第n階梯中，負荷持續的時間。具體的數值可以通過負荷曲線來計算。Pn（t）為t時段中負荷的功率。其中，峰荷出現在第1階梯，谷荷出現在第4階梯。按照以上辦法對日負荷進行分配，不僅可以使用戶每天的用電量達到均衡，而且可使用電功率保持在正常狀態［5］。除此之外，還可促使用電計劃更加準確，從而實現對低谷、峰荷的合理分配。

3 預測實例

本文以6年實際負荷為例，對一年365天中每個工作日、休息日以及節假日的負荷進行預測。因為涉及的數據龐大，因此只列出3月份的預測結果，如表1所示。

從表1中的數據可以看出，測試的結果與實際預測的結果差異較小，誤差約為3.28%。其中，最大的誤差為5.61%。在此基礎上，利用修正系數對系統進行調整，可以將誤差減小到2.9%。可見，本文的中期電力負荷預測辦法在電力系統優化調度中發揮著重要作用，值得推廣。最后，根據表1中的數據，可以制作出對應的日負荷曲線以及日持續負荷曲線。

4 結束語

綜上所述，本文采用的中期電力負荷預測辦法操作簡單，非常適用于電力系統優化調度。該預測

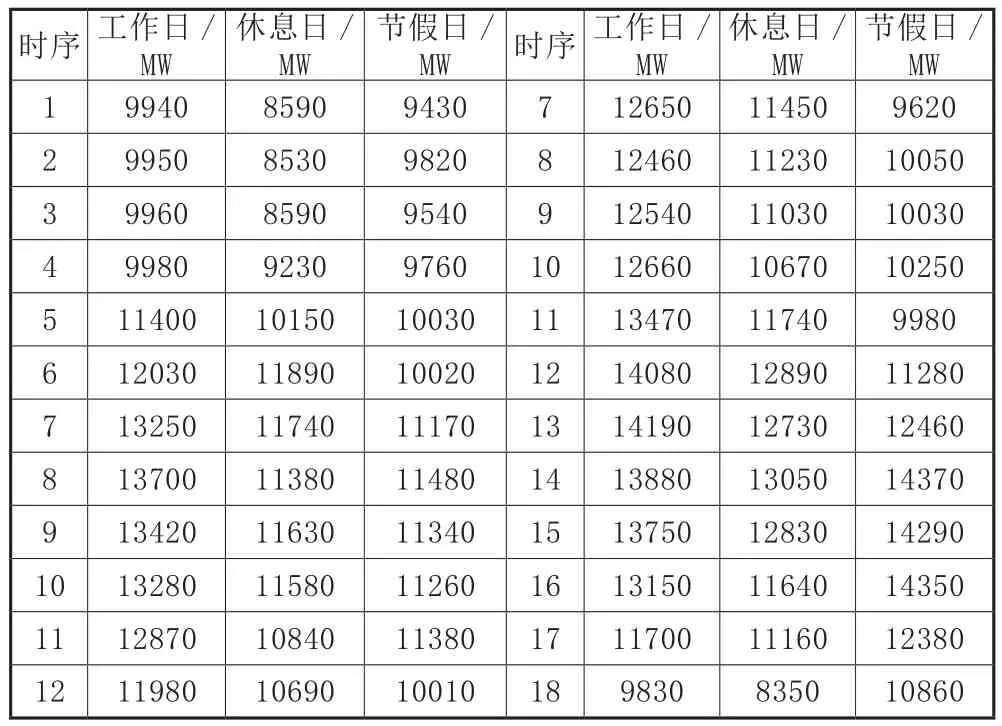
表1 工作日、休息日、節假日負荷預測（3月份）

方法不僅可以用于當年負荷預測，而且在多年負荷預測中同樣適用。根據實例分析可以看出，得出的負荷預測結果更加精準，比傳統的測試辦法具有更大的優勢。同時，采用中期電力負荷預測，保持了用電量與用電功率的均衡，實現了對低谷、峰值的合理分配。因此，這種預測方法在電力系統優化調度中具有更大的發展空間與市場。

參考文獻

［1］李軍，李青.基于CEEMDAN-排列熵和泄漏積分ESN的中期電力負荷預測研究［J］.電機與控制學報，2015，（8）：70-80.

［2］翟永杰，劉林.基于ADE-SVM和模糊理論的電力系統中期負荷預測［J］.電力系統保護與控制，2012，（8）：110-115.

［3］高翔，朱昊.變權重組合改進模型應用于中期電力負荷的預測［J］.上海電力學院學報，2013，（2）：124-128.

［4］崔和瑞，彭旭.基于ARIMAX模型的夏季短期電力負荷預測［J］.電力系統保護與控制，2015，（4）：108-114.

［5］李剛，程春田.基于SCE-UA支持向量機的短期電力負荷預測模型研究［J］.大連理工大學學報，2011，（2）：263-268.

Study on Prediction and Load Model of Power Load Mid

GUO Pingchuang
（Guangdong Power Grid Corporation Zhanjiang Power Supply Bureau of Wuchuan， Wuchuan 524500）

Abstract:In t his paper， middle power load forecasting studies on load model are discussed. First analyzes the sequence of sample loading time， and the change trend of time intervals were predicted. On this basis， established a medium-term load model. Finally， with related examples of medium load test. Practice has proved that the mid-term electric load forecasting method， optimal scheduling of power system can be implemented.

Key words:middle power load， forecast， model， research