準東煤熱解動力學單一掃描速率法應用局限性

趙　巖， 劉　栗， 邱朋華， 謝　興， 孫紹增， 劉歡鵬， 陳力哲

(哈爾濱工業大學 能源科學與工程學院， 哈爾濱 150001)

準東煤熱解動力學單一掃描速率法應用局限性

趙巖， 劉栗， 邱朋華， 謝興， 孫紹增， 劉歡鵬， 陳力哲

(哈爾濱工業大學 能源科學與工程學院， 哈爾濱 150001)

摘要:為提高單一掃描速率法在煤熱解領域的實際應用有效性，以3種不同升溫速率下準東原煤樣品的熱解失重數據為研究對象，應用單一掃描速率法進行動力學計算，分析分段觀點和失水脫氣階段失重對計算結果的影響，探討能否得到準確且唯一的動力學3因子以及動力學3因子是否具有明確的理論意義等幾個問題. 結果表明：在分段方面的不同觀點對高匹配度模式函數的類別及Arrhenius參數均具有顯著影響，連續轉化率觀點下得到的表觀活化能E明顯低于獨立轉化率觀點下的；當采用連續轉化率觀點時，排除失水脫氣階段的失重不僅影響其他階段的區間劃分，還將使E值降低；結合積分和微分法,在3個不同升溫速率下分別匹配這兩種方法，也不能獲得準確且唯一的動力學3因子，因此動力學3因子的理論意義是有限的；失重數據的預處理方法和模式函數的選擇，對于動力學參數的評價和交流是十分必要的，以動力學3因子解釋熱解機理時要十分謹慎.

關鍵詞:準東煤；熱解；動力學；單一掃描速率法；表觀活化能

對煤的熱解行為進行描述和預測以及進一步對熱解機理進行解釋是長久以來人們對熱解動力學分析的期望. 目前，非等溫法已逐漸成為研究固相反應整體動力學的主要方法，其在數學上可分為積分法和微分法；在操作方式上可分為單一掃描速率法和多重掃描速率法.

單一掃描速率法采用“模式匹配法”求解動力學3因子(活化能、頻率因子以及模式函數)，由于其在實驗操作及數學處理上相對簡便，目前在非等溫動力學分析中已占據主導地位[1-2].

長久以來，此類方法在預測過程速率和材料壽命以及為反應器設計提供性能參數等工業應用方面均發揮了重要作用，但也有文獻報道了其在實際應用方面的某些局限性. 在1996年美國費城第11屆國際熱分析和量熱會議上，ICTAC動力學工作小組發起了一個由各國熱分析工作者自愿參加的專題項目，其工作報告[3-7]指出，“許多文獻均報導了在單一掃描速率下得到的非等溫實驗數據能夠被幾組不同的動力學3因子同時匹配的現象”，同時對CaCO3熱分解失重數據的動力學計算表明，不同學者采用不同模式函數計算出的動力學參數差異很大. Vyazovkin等[1]對環四亞甲基四硝基胺(HMX)和二硝酰胺銨(AND)分解失重數據的研究結果也表明，幾個不同的模式函數均可與實驗數據匹配良好. Budrugeac等[8-10]以單一掃描速率法對單步反應的模擬數據以及聚氯乙烯(PVC)熱分解、CaC2O4·H2O加熱脫水、醋酸鋅凝膠前驅體分解的失重數據進行動力學計算時也出現了相似的情況，且他們由此提出“僅使用統計學標準(即線性相關系數)得不到真實的機理函數”. Marcilla等[11]提出“當體系中有復雜的反應存在而只能在相對窄的轉化率范圍內進行研究時，使用單一掃描速率法時會有更多的模式函數與實驗數據達到良好匹配”. 顯然，上述現象使人們無法分辨正確的模式函數，也使動力學參數的評價和比較變得困難. 盡管如此，由于單一掃描速率法突出的實際應用意義，許多學者已將其引入煤熱解領域[12-25]. 雖然到目前為止，還未見到對此類方法在煤熱解領域的多匹配現象進行詳細探討的文獻，但一些動力學計算結果已經顯現出端倪. 例如，同為大同煙煤，一些學者計算的熱解表觀活化能(E)值為61.55～239.74 kJ/mol[17]，而另一些學者則為6.322～33.591 kJ/mol[18]，二者相差6～8倍；同為平朔煙煤，一些學者給出2.942～55.059 kJ/mol的E值[18]，而另一些學者則得出E為196.3～249.9 kJ/mol[19]，二者相差4～66倍；同為兗州煙煤，一些學者得到的E值為143.65～167.86 kJ/mol[20]，而另一些學者則為12.242～56.921 kJ/mol[21]，二者相差2～11倍；同為晉東南貧煤，一些學者獲得了74.92～248.66 kJ/mol的E值[17]，而另一些學者則得出E為8.522～133.646 kJ/mol[22]，二者相差1～8倍.

煤熱解是一種極為復雜的固相反應，單一掃描速率法應用于此領域時，其局限性可能會更加突出，并可能會出現新的問題. 本文以準東煤程序升溫熱解失重數據為研究對象，分析了分段觀點和失水脫氣階段失重對計算結果的影響，得到準確且唯一的動力學3因子的可能性以及動力學3因子是否具有明確的理論意義等幾個問題，以期進一步提高單一掃描速率法在煤熱解領域的實際應用有效性.

1實驗

本文所考察的程序升溫熱解失重數據來自之前研究工作中的R-form煤[26]. 樣品的工業和元素分析如表1所示.

所用熱重系統為瑞士Mettler-Toledo公司的TGA/SDTA851e常壓熱重分析儀. 每次實驗，18 mg左右的樣品被盛裝在定制的鉑金坩堝中，在流量為80 mL·min-1的高純Ar中被加熱至1 000 ℃，采用的升溫速率分別為20、40和60 ℃·min-1.

表1　準東原煤樣品的工業分析和元素分析[26]　%

2動力學分析方法

動力學計算采用單一掃描速率法中最具代表性的Coats-Redfern積分法和Achar-Brindley-Sharp-Wendworth微分法，兩種方法的具體原理如文獻[27-29]所述. 將反應速率基本方程經過變量分離、對數變換、積分近似等一系列數學處理后，得到如下兩個等式：

(1)

(2)

式(1)為Coats-Redfern積分法方程，式(2)為Achar-Brindley-Sharp-Wendworth微分法方程. 其中f(α)和G(α)分別為微分形式和積分形式的動力學模式函數，f(α)=1/[dG(α)/dα]；α為轉化率，α=(w0-w)/(w0-w∞); w0為樣品初始質量(mg)，w為任意時刻樣品質量(mg)，w∞為樣品最終質量(mg)；T為任意時刻樣品熱力學溫度，K；β為升溫速率，K/s；R為摩爾氣體常數，8.314 J/(mol·K)；E為表觀活化能，J/mol；A為表觀頻率因子，s-1. 二者的求解過程相似：將不同的G(α)和f(α)分別代入方程(1)和(2)后，以ln[G(α)/T2]和ln[dα/(f(α)dT)]對各自的1/T作圖，之后以最小二乘法擬合數據，由直線的斜率求得E，截距求得A.

表2為單一掃描速率法中常用的一些模式函數，也是本文動力學計算的備選函數. 這里將其分為Mampel冪函數模式、Avrami-Erofeev模式、幾何相關模式、擴散模式和反應級數模式5類，分別以首字母M、A、R、D和F進行標記；每類中又根據方程特征數的不同取值分為若干子模式函數，分別以在首字母后附加一個阿拉伯數字的形式進行標記.

表2　固相反應動力學中常用的模式函數

3結果與討論

3.1問題的提出

圖1為由不同升溫速率下準東原煤熱解失重數據計算出的α-t及(dα/dT)-t曲線，其中t為T所對應的攝氏溫度. 需要說明的是，在轉化率α的計算中，樣品的初始和最終質量分別定義為程序溫度40 ℃和1 000 ℃對應的質量. 由圖1可見，各α-t及(dα/dT)-t曲線隨溫升的變化趨勢一致，均呈現4個主要階段. 以20 ℃·min-1為例進行說明：第1階段是40～230 ℃，為干燥脫氣階段，主要析出水分和物理吸附的N2和CO2等氣體，α-t曲線出現小幅上升后變得平緩，(dα/dT)-t曲線出現小峰(失水峰)；第2階段是230～350 ℃，為熱解初始階段，煤中高脂肪性的弱鍵斷裂生成小分子氣體，同時羧基發生分解析出CO2，α-t和(dα/dT)-t曲線均較為平緩；第3階段是350～620 ℃，為主熱解階段，煤基質發生廣泛的解聚和分解反應，生成大量以焦油為主的揮發分并形成半焦，α-t曲線急劇上升，(dα/dT)-t曲線在460 ℃左右出現高峰；第4階段是620 ℃以上，為2次脫氣階段，主要發生縮聚反應和芳香環小分子側鏈的脫落，半焦析出輕氣體，α-t和(dα/dT)-t曲線均逐漸變得平緩. 隨著升溫速率的提高，上述4個階段之間的分界溫度均向高溫方向發生了一定的偏移.

圖2為20 ℃·min-1時，從表1中選取的9個具有代表性的函數在整個熱解溫度區間內的Arrhenius曲線，其中α的計算范圍為0.05-0.95. 由圖2可見，當對熱解過程應用C-R積分法和A-B-S-W微分法時，各類模式函數的Arrhenius曲線均呈現明顯階段性，線性相關系數r為-0.939 7～0.942 8，總體線性度較低，這表明不能以一組不變的動力學3因子來描述整個溫度區間內準東煤的熱解失重.

(a) α-t 曲線

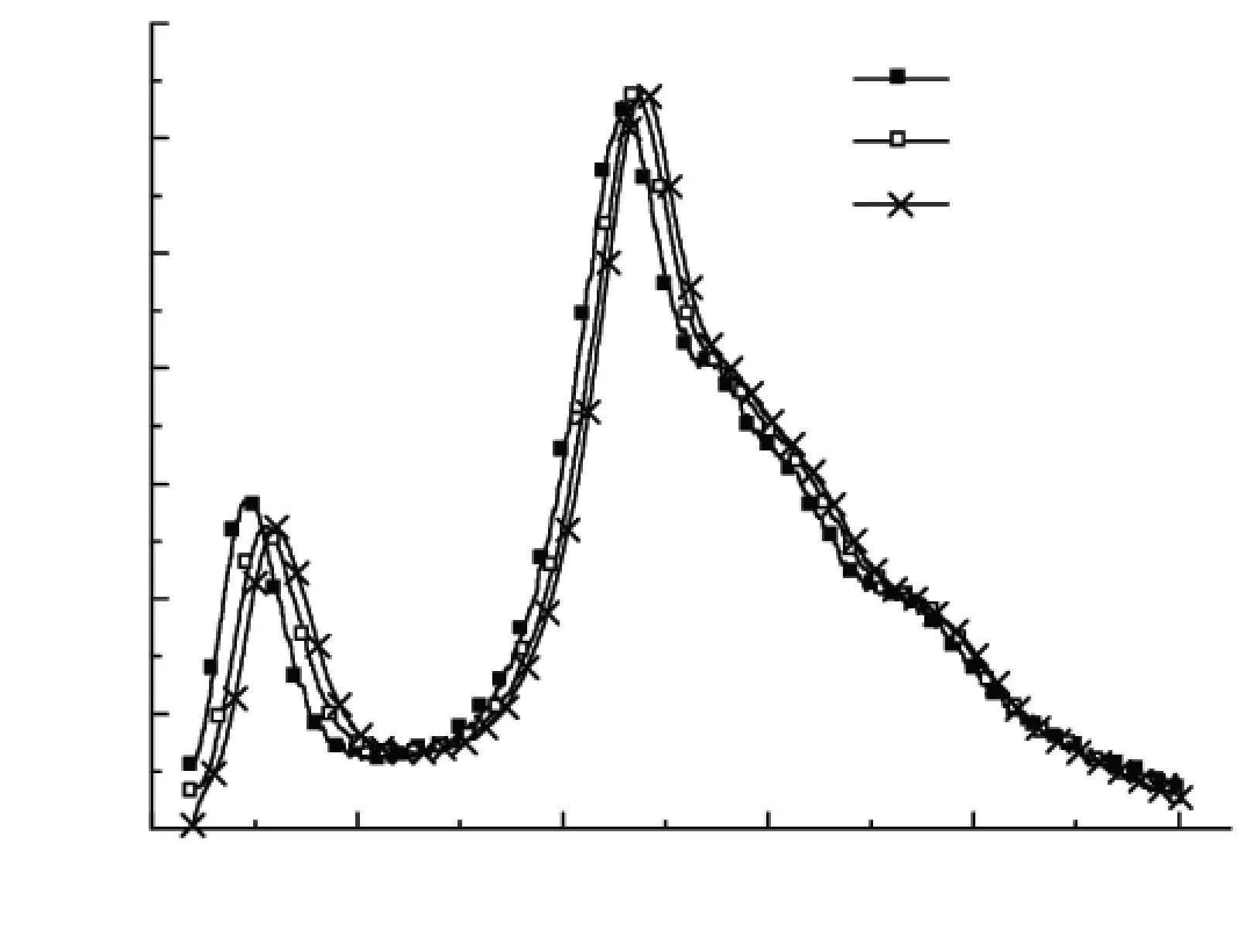
(b) (dα/dT)-t 曲線

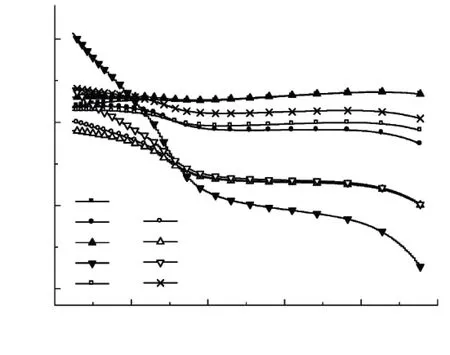
(a) C-R 法

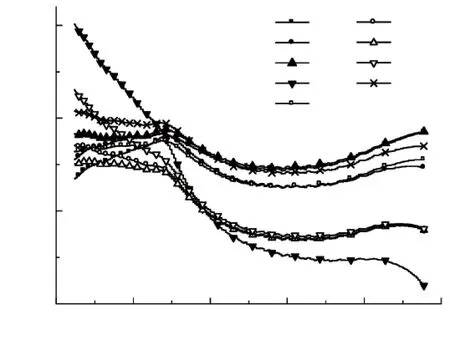
(b) A-B-S-W 法

因此，采用單一掃描速率法研究煤熱解動力學時一般均需將整個溫度范圍的失重數據做分段處理[12-25]，在每段上分別求取動力學3因子，而這就引出了實際應用中的以下幾個問題：

1)在分段方面的不同觀點對動力學計算結果有何影響?

2)能否獲得準確且唯一的動力學3因子?

3)動力學3因子是否具有明確的理論意義?

下面的內容將針對這幾個問題進行逐一探討.

3.2在分段方面的不同觀點對動力學計算結果的影響

目前以單一掃描速率法研究煤熱解動力學時，在分段方面主要有以下兩種觀點：

1)將整個溫度范圍內的失重視為一個過程，各階段的失重視為其接續進行的子過程，樣品初始溫度T0對應的α為0，最終溫度T∞對應的α為1，各階段的α取值范圍均為[0, 1]的子區間，且首尾相接[14-15]，此可稱為連續轉化率觀點.

2)將各階段失重視為獨立過程，每一階段均具有獨立的T0和T∞且α的取值范圍均為[0, 1]，彼此之間互不影響[16,19]，此可稱為獨立轉化率觀點.

然而關于兩種觀點對動力學計算結果影響的報導還很鮮見.

本文分別以上述兩種觀點對20 ℃·min-1準東原煤熱解失重數據進行劃分：

連續轉化率觀點——以Arrhenius曲線的斜率變化為依據分為4段，第1段為40～140 ℃；第2段為140～360 ℃；第3段為360～600 ℃；第4段為600～1 000 ℃；

獨立轉化率觀點——以α-t及(dα/dT)-t曲線的趨勢變化為依據分為3段，第1段為40～230 ℃；第2段為230～620 ℃；第3段為620～1 000 ℃.

對于煤熱解，最主要的考察對象是主熱解階段的動力學參數. 本文分別選取連續轉化率觀點的第3段和獨立轉化率觀點的第2段作為主熱解階段，以C-R積分法計算二者表觀活化能. 需要指出的是，對于連續轉化率觀點，由于各階段之間過渡區域的存在，在計算中舍去了區間前端的一小段溫度；對于獨立轉化率觀點，α的計算范圍為0.05～0.95. 在二者的計算過程中，均出現了若干種模式函數G(α)均可與實驗數據進行良好匹配的情況，圖3顯示了r<-0.900 0的模式函數及其對應的r和E值.

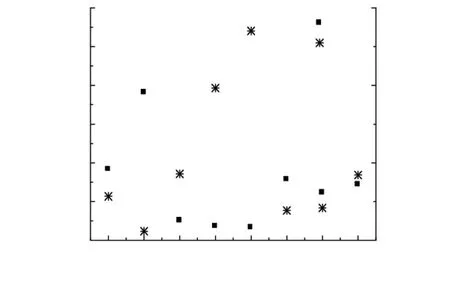
(a) 連續轉化率觀點第1部分

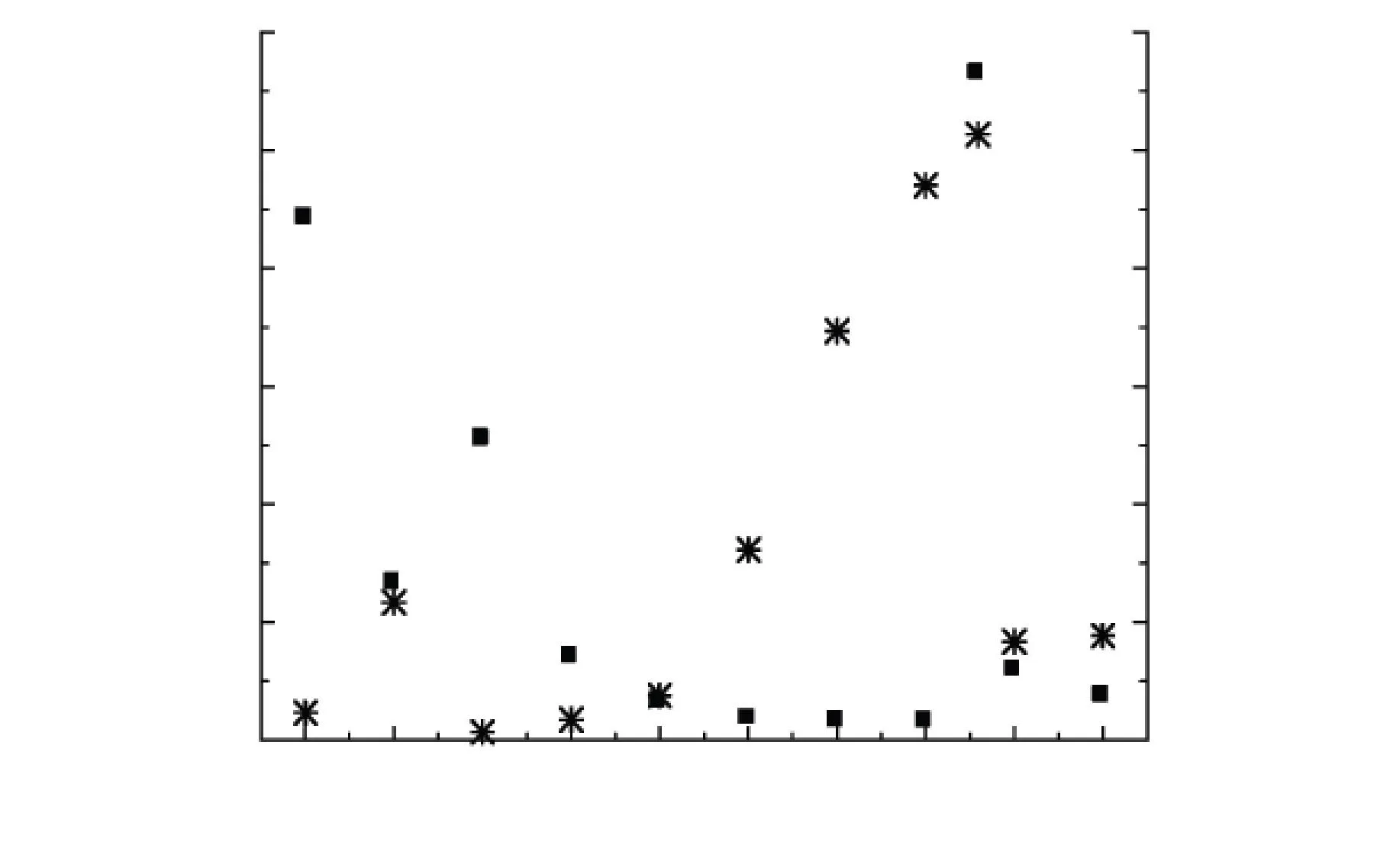
(c) 獨立轉化率觀點第1部分

(b) 連續轉化率觀點第2部分

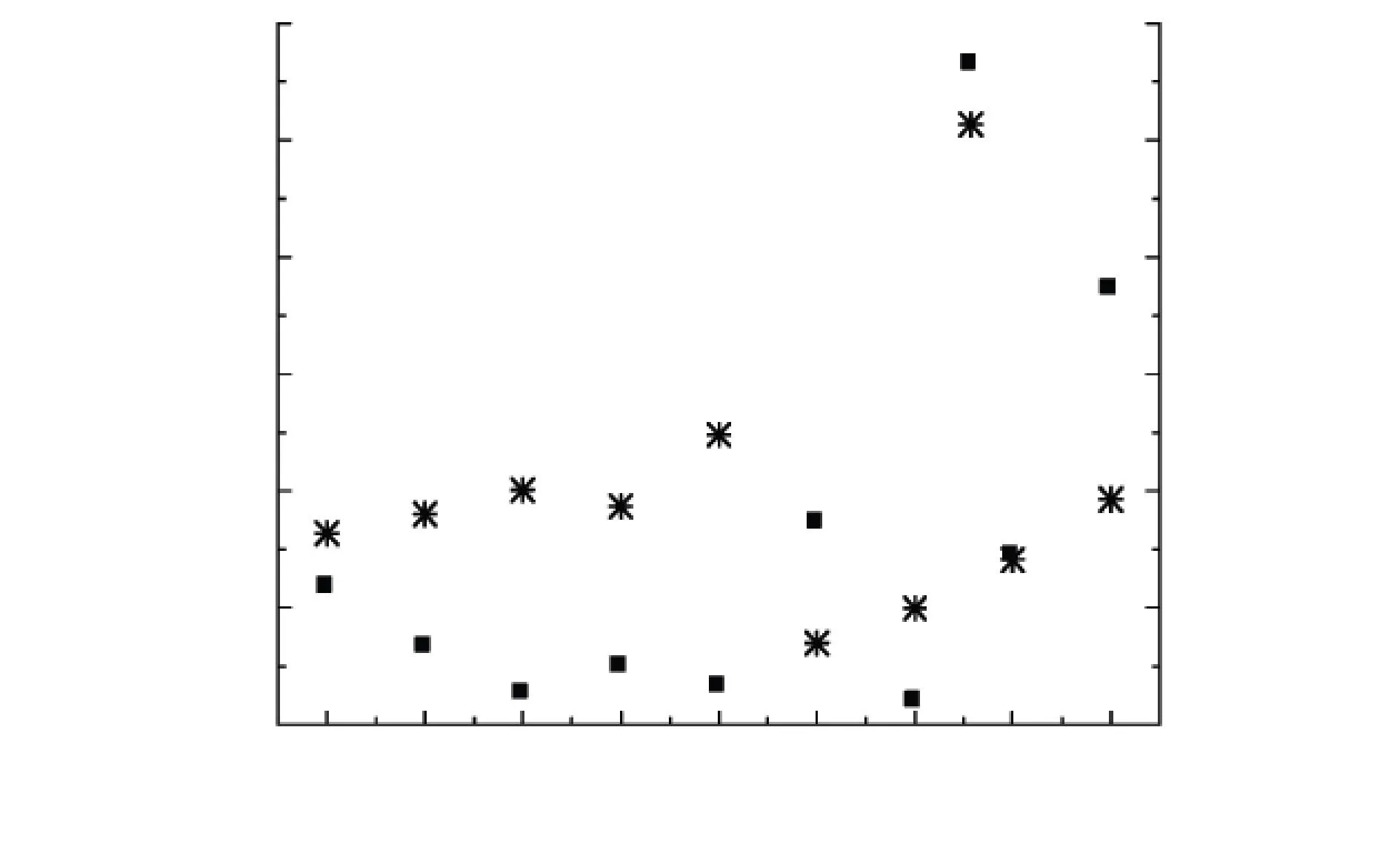
(d) 獨立轉化率觀點第2部分

由圖3可知，不同的分段觀點對主熱解階段的動力學計算產生了顯著影響，這種影響分為兩個方面：1)達到高匹配度的模式函數的變化；2)得到的Arrhenius參數的變化. 當采用連續轉化率觀點時，以r值為標準，A5、A6、D5、F3和F4均可與實驗數據達到較高匹配程度且彼此之間的匹配度差異不大，它們各自的r值分別為-0.996 4、-0.996 7、-0.997 2、-0.997 7和-0.997 2，對應的E值為98.259、135.194、68.797、36.386和50.626 kJ/mol. 當采用獨立轉化率觀點時，A4、A5、A6、D3、D5和F2也出現了類似情況，它們各自的r值分別為-0.998 2、-0.998 4、-0.998 4、-0.997 3、-0.996 7和-0.998 0，對應的E值為80.756、173.407、235.174、100.439、124.201和49.872 kJ/mol. A5、A6、D5可同時與兩種分段觀點下的實驗數據達到高匹配度，但在連續轉化率觀點下的E值均明顯低于獨立轉化率觀點. 因此，當采用單一掃描速率法研究準東煤的熱解動力學時，明確采用的分段觀點對其計算結果的有效評價和比較是十分必要的.

此外，煤的整個熱解過程包含了一個最初的失水脫氣階段，大多數學者認為這是一個物理過程，與煤熱解的主要機理——化學反應具有本質上的區別，因此在動力學計算時將此階段的失重予以忽略，即將此階段之后的某一溫度作為樣品的初始溫度T0[14-16]；而另外一些學者則認為此階段是煤整個熱解過程的組成部分，其產生的失重應該計入總失重，因此在動力學計算時予以考慮[23-25].

顯然，在獨立轉化率觀點下，是否考慮失水脫氣階段的失重對于其他階段的動力學計算沒有影響；而在連續轉化率觀點下情況則不一樣，但關于這一點的討論在相關文獻中還很少見. 本文定義20 ℃·min-1時40～230 ℃為失水脫氣階段. 在連續轉化率觀點下，仍然選取主熱解階段C-R積分法計算中r<-0.900 0的模式函數，其考慮和不考慮失水脫氣階段時得到的r和E值分別如圖3(a)和4所示. 值得注意的是，在排除此階段的失重后，一些模式函數可以對主熱解和二次脫氣階段總體進行良好的匹配，即在連續轉化率觀點下，考慮失水脫氣階段與否將會對其他階段的劃分產生直接影響，因此圖4的計算結果也包含了二次脫氣階段.

由圖3(a)和圖4的對比可以看出，D5、F3、F4能夠同時與考慮和不考慮失水脫氣階段的實驗數據匹配良好且彼此之間的匹配度差異很小. 對于前者，它們各自的r值分別為-0.997 2、-0.997 7和-0.997 2，對應的E值為68.797、36.386和50.626 kJ/mol；對于后者，r值分別為-0.991 4、-0.996 7和-0.988 1，對應的E值為31.582、15.413和24.136 kJ/mol. 由此可見，排除失水脫氣階段的失重不僅能夠影響其他階段的區域劃分，還將使得到的E值降低. 因此，對于此種情況下準東煤熱解動力學參數的正確評價和比較，明確是否排除了失水脫氣階段的失重是十分必要的.

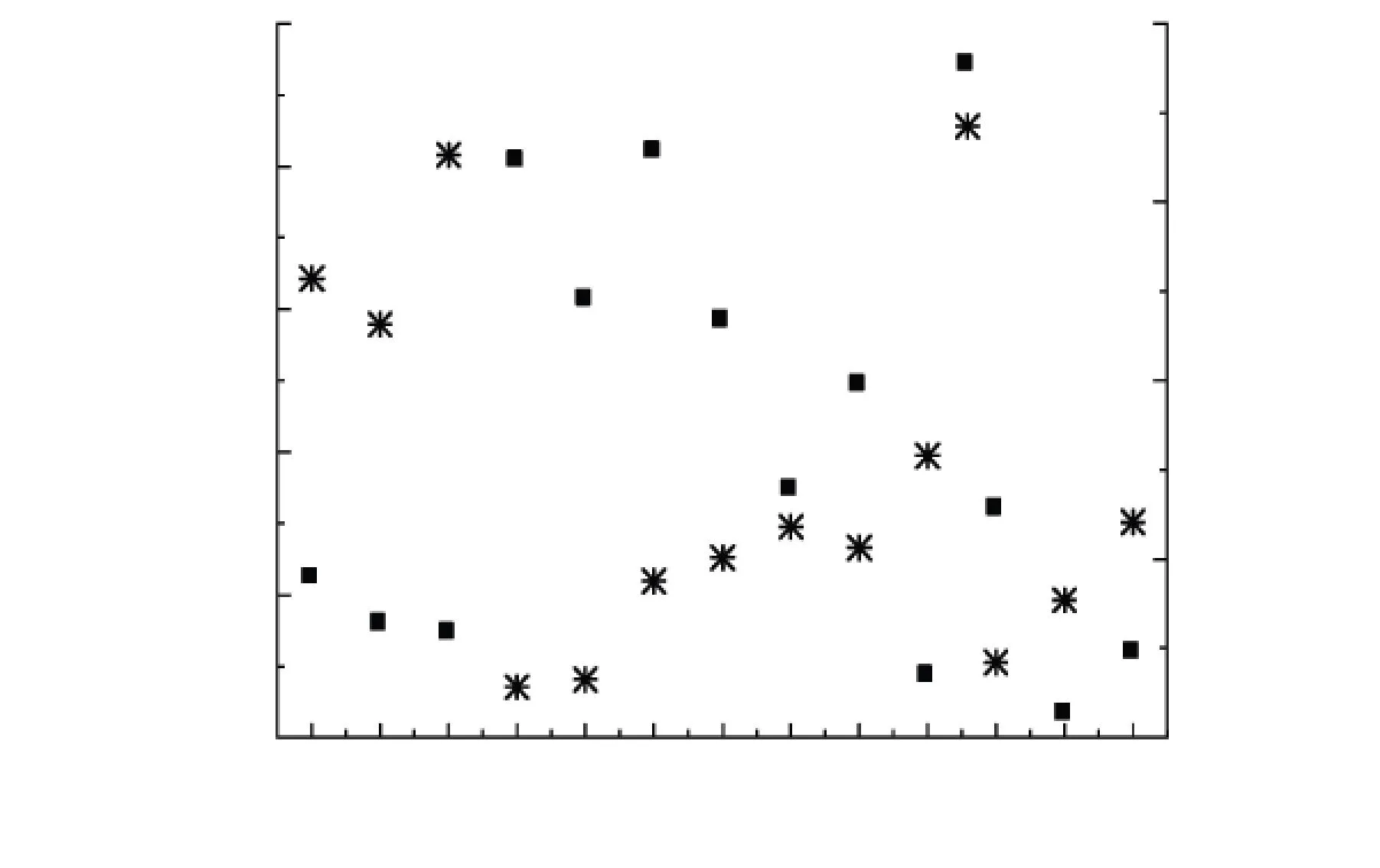
圖4不考慮失水脫氣階段的主熱解和二次脫氣階段總r和E值

3.3獲得準確且唯一的動力學3因子的可能性討論

目前，對單一掃描速率法得到的動力學三因子準確程度評價的主要標準是統計學上的線性相關系數r，|r|越接近1，則認為所選取的模式函數G(α)或f(α)越接近實際，得到的Arrhenius參數越準確. 然而,由前面的研究結果可知，當對準東煤的熱解過程進行分段處理后，單獨應用積分法或微分法時會出現多個模式函數均可與實驗數據進行準確匹配，且得到的動力學參數差異很大的現象，這就為準東煤熱解動力學參數的正確評價和比較帶來了困難. 上述現象可簡稱為多匹配局限性. 為了克服此局限性而獲得準確且唯一的動力學3因子，一些學者進行了相關研究. Bagchi等[30]提出采用積分和微分法相結合的方法確定反應模式函數；Criado等[31]提出使用C-R積分方程與A-B-S-W微分方程相結合的方法來篩選出正確的模式函數；另一些文獻[4,32]推薦在幾個不同的升溫速率下分別對失重數據進行匹配來獲得準確的模式函數. 本文將對準東煤的主熱解階段失重數據同時應用C-R積分方程與A-B-S-W微分方程相結合和在3個不同升溫速率下分別匹配這兩種方法，以驗證它們的有效性. 本文定義當C-R法和A-B-S-W法得到的r值均小于-0.985 0且相應的E值之間的相對誤差不超過10%的G(α)或f(α)為準確的模式函數.

圖5為分別以C-R法和A-B-S-W法對獨立轉化率分段觀點20 ℃·min-1主熱解階段失重數據進行處理，r均小于-0.900 0的模式函數所對應的r和E值. 由圖5可見，采用積分和微分法相結合的方式對于篩選出正確的模式函數具有一定幫助，一些在單獨應用積分法時匹配度很高的模式函數，在應用微分法時匹配度下降而被排除. 然而，這仍然不足以獲得準確且唯一的模式函數. 對于A4、A5、A6、D3和D5，其積分法r值分別為-0.998 2、-0.998 4、-0.998 4、-0.997 3和-0.996 7，相應的微分法r值為-0.995 0、-0.998 0、-0.998 3、-0.993 3和-0.994 5，均達到很高的匹配度；對應的E值相對誤差分別為6.61%、3.19%、2.37%、0.56%和8.35%. 因此它們都是足夠準確的模式函數，但不難發現它們彼此的E值差異很大.

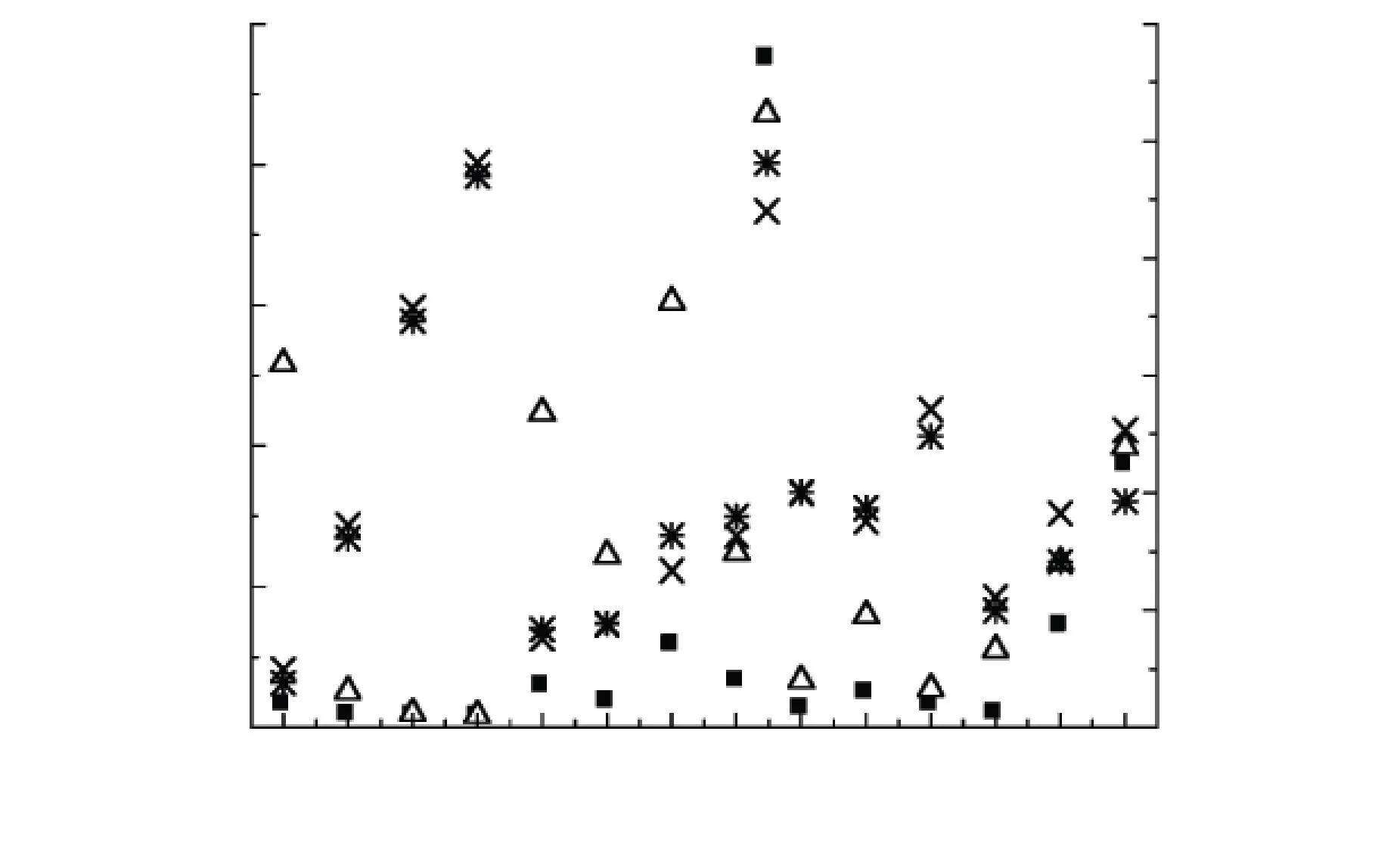
圖5主熱解階段C-R法及A-B-S-W法r<-0.900 0模型函數的r和E值

圖6為分別以C-R法和A-B-S-W法對獨立轉化率分段觀點40和60 ℃·min-1主熱解階段失重數據進行處理，r均小于-0.900 0的模式函數所對應的r和E值. 由圖6(a)可知，在40 ℃·min-1升溫速率下，準確的模式函數為A4、A5、A6、D3和D5，其積分法r值分別為-0.997 9、-0.998 2、-0.998 3、-0.995 3和-0.998 0，對應的微分法r值為-0.992 5、-0.997 3、-0.997 9、-0.988 7和-0.995 1；相應的E值相對誤差為3.64%、1.72%、1.27%、3.45%和6.61%. 由圖6(b)可知，在60 ℃·min-1升溫速率下，準確的模式函數為A4、A5、A6和D5，其積分法r值分別為-0.996 3、-0.997 1、-0.997 2和-0.998 4，對應的微分法r值為-0.989 4、-0.995 7、-0.996 5和-0.995 0；相應的E值相對誤差為0.07%、0.03%、0.02%和4.54%. 此外，A4、A5、A6和D5的E值隨升溫速率的變化均很小. 由此可見，通過積分和微分法相結合與3個不同升溫速率下分別匹配這兩種方法的同時運用，仍然存在4個模式函數A4、A5、A6和D5能夠與實驗數據匹配良好，但相應的E值差異很大，因此無法獲得準確且唯一的動力學參數.

造成單一掃描速率法的多匹配局限性的根本原因是，其反應速率基本方程是由等溫單步反應速率方程演化而來，而等溫單步反應的基本假設是與實際非等溫固相反應的復雜多步本質相悖的. 由反應速率方程可知，過程速率是T和α的函數，其對T的依賴性由速率常數k(T)即Arrhenius方程體現，而對α的依賴性則由模式函數f(α)體現. 將非等溫數據以假定的模式函數f(α)進行匹配時，Arrhenius參數由假定的f(α)的形式所決定. 在非等溫實驗中，T和α同時變化，而單一掃描速率法不能將k(T)和f(α)進行有效地分離，因此只能同時而不是分步地求解動力學3因子，這樣就導致了若干G(α)或f(α)均可以通過以Arrhenius參數強烈變化為代價的方式補償它們與真實模式函數之間的差異，從而對數據進行在統計學上準確的匹配，進而得到高度分散的Arrhenius參數. 準東煤的熱解作為一種包含多種反應路徑的復雜固相反應，在對其非等溫實驗數據進行模式匹配時，此種補償效應尤為顯著，以至于同時運用積分和微分法相結合與在3個不同升溫速率下分別匹配這兩種被認為在一般非等溫固相反應中可以通過增加額外的限制而有效削弱補償效應的方法，也不能獲得準確且唯一的動力學3因子. 因此，當采用單一掃描速率法研究準東煤的熱解動力學時，明確選用的模式函數對于動力學參數的正確評價和比較是十分必要的.

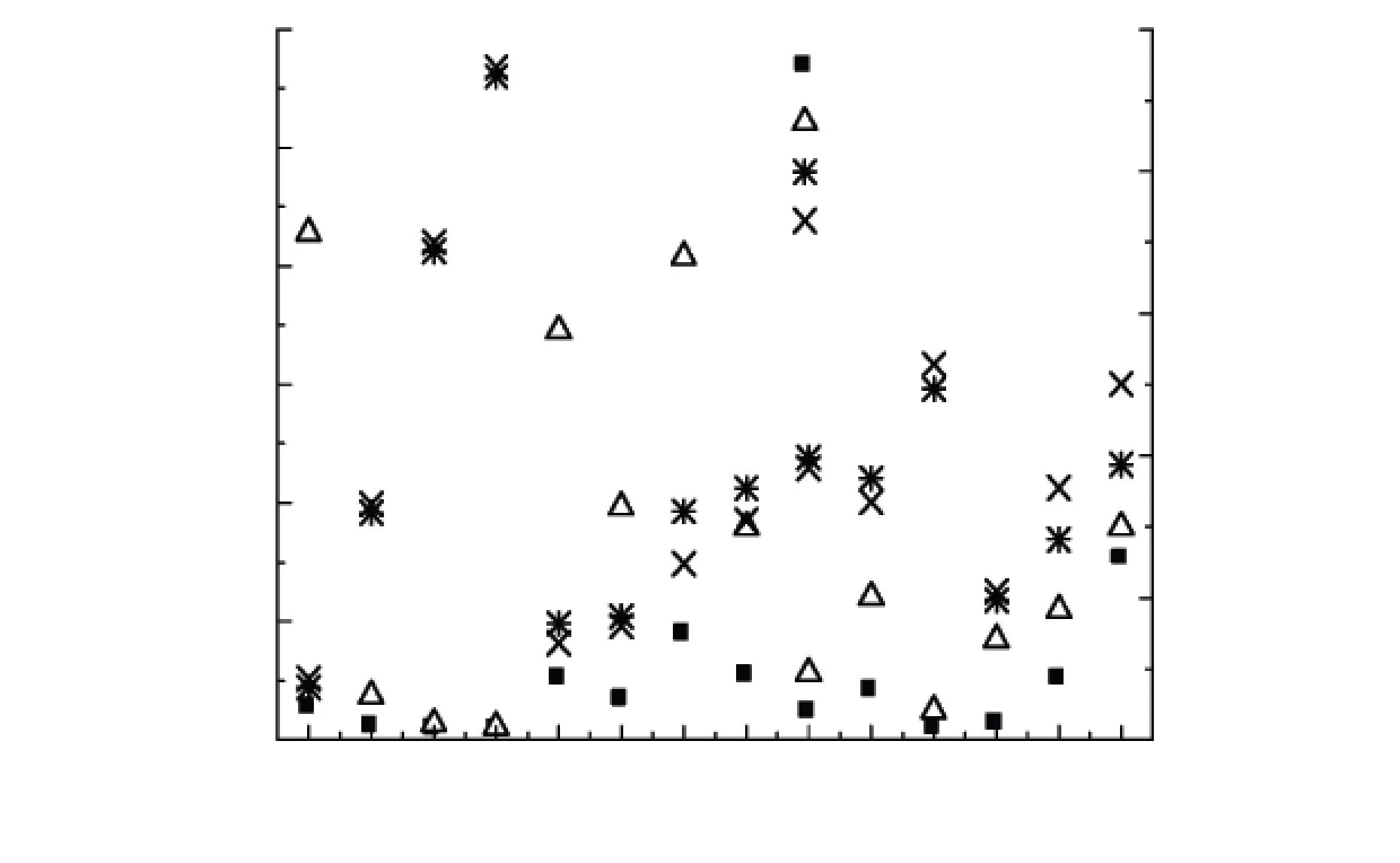
(a) 40 ℃·min-1

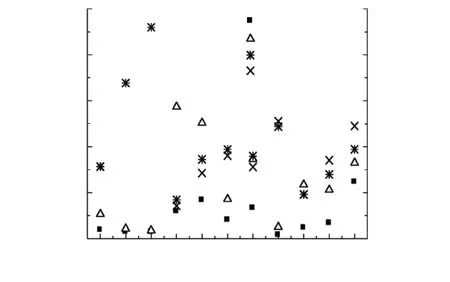
(b) 60 ℃·min-1

圖640 ℃·min-1和60 ℃·min-1下主熱解階段C-R法及A-B-S-W法r<-0.900 0模型函數的r和E值

3.4動力學3因子理論意義的探討

反應模式函數可以確定反應機理，同時相應的Arrhenius參數可以由過渡態理論進行合理地詮釋，是人們對于單一掃描速率法的最重要期望之一. 然而本文的研究結果表明，這種期望對于準東煤熱解的動力學研究是不切實際的.

首先，這種期望是源于等溫單步反應動力學的基本假設，而這是與準東煤熱解的實際過程相悖的. 準東煤熱解是一個包括了橋鍵斷裂、交聯、氫傳輸、取代、縮聚等極為復雜的反應體系，除此之外，其還耦合了傳熱和傳質等物理過程. 轉化率α以總失重量的分數來表征過程的總包轉化程度，因此其包含了以上全部過程的影響. 通過以α為自變量的模式函數在統計學上的匹配求得的表觀Arrhenius參數，應該是各獨立基元反應的Arrhenius參數、額外的物理過程的等效Arrhenius參數、以及各基元反應和物理過程的相對貢獻度的復雜函數. 隨著α和T的變化，各基元反應及物理過程對表觀轉化速率的貢獻度將發生變化，表觀Arrhenius參數和過程控制機理將改變，而單一掃描速率法獲得的表觀Arrhenius參數和模式函數在某個區間內是不變的，這樣的動力學參數僅僅是對某個階段樣品表觀失重行為的總體近似描述，而對揭示過程的反應機理幫助甚微. 此外，由前面的研究結果可知，往往幾個模式函數可以同時完成對實驗數據的良好匹配，但彼此之間的E值差異很大，說明以統計學標準看,能夠準確描述實驗數據的動力學三因子并非唯一，進一步表明它們的作用僅僅是再現實驗數據，而其物理意義是模糊不清的.

其次，“模式函數匹配”這種方法本身存在一定的局限性. 因為每一個“準確的”模式函數，均是從一個由有限個備選函數人為組建的列表中篩選出來，而在此之前無法確定列表中是否已經包含了那個最接近實際的“最佳匹配”模式函數. 換言之，由此得到的“準確的”模式函數，永遠只是相對于列表中的其他函數而言，并非絕對意義上的“準確”.

第三，各類模式函數本身對于實際固相反應的描述具有一定局限性. 目前,使用的模式函數絕大多數采用了反應物顆粒具有規整的幾何形狀和各向同性的反應活性的基本假設[33]，此外為了簡化計算還可能附加一些特殊假設，然而隨著現代物理化學測試技術的飛速發展，一些實驗數據已經證明這些假設對于某些固相反應并不適用. 例如Mampel的關于分解反應物的每個顆粒只產生一個核的假設，在今天電子顯微鏡得到的證據看來是不切實際的[4]；Jander三維擴散模式假設具有規整立方體或球狀的樣品顆粒的反應界面沿著三維方向由外向內各向同性地等速推進，但是近年來用掃描電子顯微鏡技術對一些金屬鹽類的分解和脫水過程進行直接觀察的結果證明實際情況并非如此[34-35]. 準東煤是一種結構復雜的非勻質固相反應物，熱重實驗中其顆粒的幾何形狀并非規整，堆積狀況也非規則，這些因素均會使其失重行為偏離各類模式函數的描述.

最后，甚至一些模式函數本身與反應機理之間的對應關系也很模糊. Dollimore[36]指出幾種完全不同的機理可以生成同一個模式函數以及同一種機理能夠產生幾種模式函數；實際上，本文表3中的A類和F類模式函數在某些情況下是相似的，例如當二者的n均為1時，它們具有相同的數學形式，然而卻具有不同的物理意義.

綜上所述，由于準東煤熱解的復雜多步本質以及模式函數匹配法本身的局限性，由單一掃描速率法得到的動力學3因子的理論意義是十分模糊的，很難將模式函數與過程機理相聯系，也很難將Arrhenius參數作為過程的固有特征而與能量壁壘或活化絡合物的振動頻率等過渡態理論中的概念相聯系. 因此，在使用它們解釋熱重實驗過程中準東煤熱解的控制機理時要十分謹慎.

4結論

1)對于準東煤的熱解，在分段方面的不同觀點對高匹配度模式函數的類別及Arrhenius參數均具有顯著影響，連續轉化率觀點下得到的表觀活化能E明顯低于獨立轉化率觀點.

2)當采用連續轉化率觀點時，排除失水脫氣階段的失重不僅能夠影響其他階段的區間劃分，還將使得到的E值降低.

3)同時運用積分和微分法相結合與在3個不同升溫速率下分別匹配這兩種方法，也不能獲得準確且唯一的動力學3因子，因此動力學3因子的理論意義是有限的.

4)闡明失重數據的預處理方法和模式函數的選擇，對于動力學參數的評價和交流是十分必要的，同時以動力學3因子解釋熱解機理時要十分謹慎.

致謝

感謝國家自然科學基金項目《我國低階煤煤焦低溫氣化反應性的研究》(批準號51376053)和國家自然科學基金委創新研究群體項目《熱輻射傳輸與流動控制》(批準號51421063)對本文研究工作的支持.

參考文獻

[1] VYAZOVKIN S, WIGHT C A. Model-free and model-fitting approaches to kinetic analysis of isothermal and nonisothermal data[J]. Thermochimica Acta, 1999, 340: 53-68.

[2] OPFERMANN J R, KAISERSBERGER E, FLAMMERSHEIM H J. Model-free analysis of thermoanalytical data-advantages and limitations[J]. Thermochimica Acta, 2002, 391(1): 119-127.[3] BROWN M E, MACIEJEWSKI M, VYAZOVKIN S, et al. Computational aspects of kinetic analysis: part A: the ICTAC kinetics project-data, methods and results[J]. Thermochimica Acta, 2000, 355(1): 125-143.

[4] MACIEJEWSKI M. Computational aspects of kinetic analysis: part B: The ICTAC kinetics project—the decomposition kinetics of calcium carbonate revisited, or some tips on survival in the kinetic minefield[J]. Thermochimica Acta, 2000, 355(1): 145-154.[5] VYAZOVKIN S. Computational aspects of kinetic analysis: part C: The ICTAC kinetics project—the light at the end of the tunnel?[J]. Thermochimica Acta, 2000, 355(1): 155-163.

[6] BURNHAM A K. Computational aspects of kinetic analysis: part D: The ICTAC kinetics project—multi-thermal-history model-fitting methods and their relation to isoconversional methods[J]. Thermochimica Acta, 2000, 355(1): 165-170.

[7] RODUIT B. Computational aspects of kinetic analysis: part E: The ICTAC kinetics project—numerical techniques and kinetics of solid state processes[J]. Thermochimica Acta, 2000, 355(1): 171-180.

[8] BUDRUGEAC P, SEGAL E. Some methodological problems concerning nonisothermal kinetic analysis of heterogeneous solid-gas reactions[J]. International Journal of Chemical Kinetics, 2001, 33(10): 564-573.[9] MUAT V, BUDRUGEAC P, MONTEIRO R C C, et al. Non-isothermal kinetic study on the decomposition of Zn acetate-based Sol-gel precursor. Part Ⅰ. Application of the isoconversional methods[J]. Journal of thermal analysis and calorimetry, 2007, 89(2): 505-509.

[13]LU Yongkang, CHANG Liping, XIE Kechang. Effects of coal structure on its pyrolysis characteristics under N2and Ar atmosphere[J]. Energy Sources, 2001, 23(8): 717-725. [14]ARENILLAS A, RUBIERA F, PEVIDA C, et al. A comparison of different methods for predicting coal devolatilisation kinetics[J]. Journal of Analytical and Applied Pyrolysis, 2001, 58-59: 685-701.

[16]LIU Quanrun, HU Haoquan, ZHOU Qiang, et al. Effect of inorganic matter on reactivity and kinetics of coal pyrolysis[J]. Fuel, 2004, 83: 713-718.

[17]何佳佳. 反應條件對煤揮發分析出過程影響的TG-FTIR分析[D]. 哈爾濱: 哈爾濱工業大學, 2007: 54-55.

[18]降文萍. 煤熱解動力學及其揮發分析出規律的研究[D]. 太原: 太原理工大學, 2004: 59-62.

[19]吳波. 神東和平朔煤在不同反應器中的熱解特性[D]. 大連: 大連理工大學, 2009: 42-43.

[20]王俊琪, 方夢祥, 駱仲泱, 等. 煤的快速熱解動力學研究[J]. 中國電機工程學報, 2007, 17: 18-22.

[21]張妮, 曾凡桂, 降文萍. 中國典型動力煤種熱解動力學分析[J]. 太原理工大學學報, 2005 (5): 549-552.

[22]曾光. 我國典型低揮發分煤熱解成分的定量分析[D]. 哈爾濱: 哈爾濱工業大學, 2008: 44-45.

[23]李爽, 楊斌, 馮秀燕, 等. 典型陜北長焰煤熱解行為及其動力學實驗研究[J]. 大連理工大學學報, 2013, 53(3): 333-339.

[24]宋紹勇. 煤熱解動力學及其機理的實驗研究[D]. 太原: 太原理工大學, 2002: 34-39.

[25]陳燕. 東烏旗煤及不同化學組分熱解動力學及其揮發分析出規律研究[D]. 太原: 太原理工大學, 2011: 43-44.

[26]邱朋華, 趙巖, 陳希葉, 等. 堿及堿土金屬對準東煤熱解特性及動力學影響分析[J]. 燃料化學學報, 2014, 10: 1178-1189.

[27]COATS A W, REDFERN J P. Kinetic parameters from thermogravimetric data[J]. Nature, 1964, 201: 68-69.

[28]ACHAR B N N, BRINDLEY G W, SHARP J H. Kinetics and mechanism of dehydroxylation processes. III. Applications and limitations of dynamic methods[C]//Proc Int Clay Conf. Jerusalem: Israel University Press, 1966: 67-70.

[29]SHARP J H, WENTWORTH S A. Kinetic analysis of thermogravimetric data[J]. Analytical chemistry, 1969, 41(14): 2060-2062.

[30]BAGCHI T P, SEN P K. Combined differential and integral method for analysis of non-isothermal kinetic data[J]. Thermochimica Acta, 1981, 51(2): 175-189.

[31]CRIADO J M, ORTEGA A. Remarks on the discrimination of the kinetics of solid-state reactions from a single non-isothermal trace[J]. Journal of thermal analysis, 1984, 29(6): 1225-1236.

[32]CABALLERO J A, CONESA J A. Mathematical considerations for nonisothermal kinetics in thermal decomposition[J]. Journal of analytical and applied pyrolysis, 2005, 73(1): 85-100.[33]胡榮祖, 高勝利, 趙鳳起, 等. 熱分析動力學[M]. 2版. 北京: 科學出版社, 2008: 4-6.

[34]TANAKA H. Thermal analysis and kinetics of solid state reactions[J]. Thermochimica Acta, 1995, 267: 29-44.

[35]KOGA N, TANAKA H. Effect of sample mass on the kinetics of thermal decomposition of a solid. Part 3. Non-isothermal mass-loss process of molten NH4NO3[J]. Thermochimica Acta, 1994, 240: 141-151.

[36]DOLLIMORE D. The application of thermal analysis in studying the thermal decomposition of solids[J]. Thermochimica Acta, 1992, 203: 7-23.

(編輯楊波)

Application limitations of single scanning rate method in pyrolysis kinetics of Zhundong coal

ZHAO Yan, LIU Li, QIU Penghua, XIE Xing, SUN Shaozeng, LIU Huanpeng, CHEN Lizhe

(School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China)

Abstract:To improve the application effectiveness of single scanning rate method in the coal pyrolysis field, the weight loss data of temperature programmed pyrolysis of Zhundong coal at three heating rates were investigated and the kinetic parameters were calculated using single scanning rate methods. Several problems such as the impacts of segmentation viewpoint and weight loss in the dehydration and degassing stage on the kinetics calculation results, the possibility of obtaining an accurate and unique kinetic triplet and the theoretical significance of kinetic triplet were analyzed. The results show that the selected segmentation viewpoint affects the well-fitted model functions and Arrhenius parameters, the apparent activation energy (E) values based on sequential conversion viewpoint are obviously lower than those based on independent conversion viewpoint. When the sequential conversion viewpoint is used, excluding the weight loss in dehydration and degassing stage affects the intervals of the other stages and reduces the E values. The comprehensive application of the integral and differential methods as well as the three heating rates can not provide an accurate and unique kinetic triplet, so the theoretical significance of kinetic triplet is limited. Clarifying the pretreatment method of weight loss data and model function chosen are quite necessary for the evaluation and communication of kinetic parameters, and the explanations of pyrolysis mechanism using kinetic triplets should be made with extreme care.

Keywords:Zhundong coal; pyrolysis; kinetics; single scanning rate method; apparent activation energy

doi：10.11918/j.issn.0367-6234.2016.07.009

收稿日期:2015-09-16

基金項目:國家自然科學基金(51376053);

作者簡介:趙巖(1985—)，男，博士研究生；

通信作者:邱朋華，qiuph@hit.edu.cn

中圖分類號:TQ522

文獻標志碼:A

文章編號:0367-6234(2016)07-0058-09

國家自然科學基金委創新研究群體(51421063)

邱朋華(1973—)，男，教授，博士生導師；

孫紹增(1963—)，男，教授，博士生導師