含三體相互作用XX模型的測量誘導非局域性

謝玉霞, 劉　晶

(西安郵電大學 理學院, 陜西 西安 710121)

含三體相互作用XX模型的測量誘導非局域性

謝玉霞, 劉晶

(西安郵電大學 理學院, 陜西 西安 710121)

摘要:利用Bures距離測量誘導非局域性的概念研究含三體相互作用海森堡XX鏈的非局域性，討論增強系統邊界量子比特之間測量誘導非局域性的可調參數。對有限溫度下的系統熱平衡態，通過優化調節XZX+YZY或XZY-YZX型三體相互作用的強度和外加勻強磁場的強度，對應邊界量子比特之間的Bures距離測量誘導非局域性得到有效提高。該結論可用于實現量子自旋系統的非局域性調控。

關鍵詞:測量誘導非局域性；海森堡XX模型；三體相互作用

量子關聯不僅是量子力學區別于經典物理的一個根本特性，同時也是重要的量子信息處理物理資源，在量子通信、量子計算和量子度量學等新興量子技術中發揮著不可替代的作用，從而成為多年來人們持續關注的一個熱點問題。對量子態的關聯屬性，可以從不同的角度來加以刻畫和度量。截至目前，人們提出的比較有代表性的量子關聯度量方案有非局域性、量子糾纏和量子失諧等[1-2]，它們分別從不同的側面揭示了量子態的新奇性質，同時在量子信息處理任務中也有著不同的潛在應用。

非局域性刻畫的是量子系統區別于經典物理系統的一種重要屬性，例如考慮空間距離足夠遠的兩體量子系統，對其一個子系的測量可以即刻影響另一個子系的狀態。對非局域性的探討始于愛因斯坦等人關于EPR佯繆的假想實驗[3]，代表性的進展則是基于局域因變量理論提出的各類貝爾不等式[4]及其實驗驗證[5]，以及對貝爾不等式與量子糾纏關系的討論[6-7]。它們不僅將非局域性問題的研究發展到了定量化的層面，更是將整個量子力學學科推進到了一個全新的高度。

除了基于貝爾不等式的非局域性，最近，駱順龍等人又從信息學角度提出了測量誘導非局域性(measurement-inducednonlocality,MIN)的概念[8]。它基于測量引起量子態塌縮的量子力學基本原理，定義量子非局域性的大小為局域不變測量后系統整體量子態相對于測量前系統整體量子態的最大希爾伯特-施密特距離的平方。之后，人們又提出了基于雙邊投影測量的MIN度量方案[9]，但是它們并不滿足局域操作下的單調性要求。為避免上述問題，人們對其進行了改進并證明了馮·紐曼熵[10]、跡距離和Bures距離[11]等可作為好的非局域性度量函數。對MIN與Unruh效應[12]、MIN的單配性[13]、束縛糾纏態的MIN[14]，以及開放系統中的MIN動力學演化問題[15-17]，人們也進行了仔細的研究。

本文將討論包含三體相互作用時海森堡XX模型邊界量子比特的非局域性，并主要關注XZX+YZY和XZY-YZX兩種不同類型的三體相互作用對Bures距離MIN的影響，目的是找出最佳的系統參數，為實現該系統中非局域性的有效調控提供理論支撐。

1理論模型及MIN的計算

自旋鏈系統是凝聚態物理中研究較多的一個物理系統。作為實現量子計算的重要備選物理體系，近年來它也受到了量子信息學領域研究者的廣泛關注。研究該類系統中的非局域特性及其調控問題具有理論和現實意義。

三體相互作用是存在于自旋鏈系統的一種重要相互作用，也可以通過光晶格系統來模擬實現[18]。近年來，三體相互作用對量子糾纏、量子失諧等的影響引起了人們極大的關注[19-20]。考慮含XZX+YZY和XZY-YZX兩種不同類型三體相互作用的自旋-1/2海森堡XX模型，對應的系統哈密頓量可以寫為

采用開邊界條件，并具體考察有限溫度下系統熱平衡態對應的邊界量子比特(即第1和第N個)之間Bures距離MIN對三體相互作用強度α和β的依賴關系。

對于給定的系統哈密頓量，若求得其能量本征值Ei和能量本征態|ψi〉(i=1,2,…,2N)，則系統的熱平衡態可以寫為

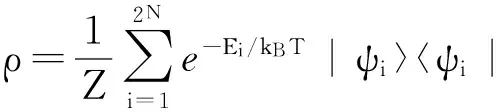
其中kB表示玻爾茲曼常數，T表示系統溫度，Z則代表配分函數，其形式為

式中當T=0時默認取e-Ei/kBT=1，這意味著

e-Ei/kBT/Z=1/2N，

即在絕對零度時所有可能的態|ψi〉都以相同的概率出現。

有了系統熱平衡態密度算子ρ之后，通過求解其約化密度算子

ρ1N=tr2,…,N-1ρ，

便可以計算其邊界量子比特之間的非局域性。選擇Bures距離MIN來度量非局域性的大小，它已被證明滿足一般非局域性度量的全部性質，其定義為[11]

式中

NB(ρBell)=1。

對于約化密度算子ρA非兼并的情形，最優測量算子實際上對應ρA的譜分解，即

其中

σ=(σ1,σ2,σ3),x=(x1,x2,x3),

xi=tr(ρ σi) (i=1,2,3)。

對于ρA=IA/2兼并的情形，則Bures距離MIN的計算只能對所有可能的測量算子

進行最優化，式中u∈3表示三維空間中的單位矢量。具體進行數值計算時，在球坐標系中將其寫為

u=(sinθcosφ,sinθsinφ,cosθ)。

其中參數θ∈[0,2π]，φ∈[0,π]。

2結果和討論

討論不同外加磁場下，Bures距離MIN對三體相互作用強度的依賴關系。數值結果表明NB(ρ1N)與J的正負無關，因此為了討論方便，取J=1。

首先，考察XZX+YZY型三體相互作用對系統熱平衡態Bures距離MIN的影響。不同磁場強度和不同量子比特數下NB(ρ1N)對三體相互作用強度α的依賴關系曲線如圖1所示,其中系統參數kBT=0.5。當不加外磁場時，系統邊界量子比特之間的Bures距離MIN隨著α的增大先是逐漸增大，當α達到某一臨界值αc1時，NB(ρ1N)達到其峰值，這里αc1隨量子比特數的增加而單調的減小。當α>αc1時，對三量子比特和四量子比特情形，NB(ρ1N)隨α的增大而逐漸的減小；而對于五量子比特和六量子比特情形，隨著α的增大，NB(ρ1N)先在α=αc2處衰減為零，當α>αc2時，NB(ρ1N)再次增加并最終趨近于其穩態平衡值。值得注意的是，該平衡值要大于α=αc1時NB(ρ1N)的峰值。最后，當量子比特數N≥7時，隨著三體相互作用強度的增大，NB(ρ1N)會出現多個峰值。

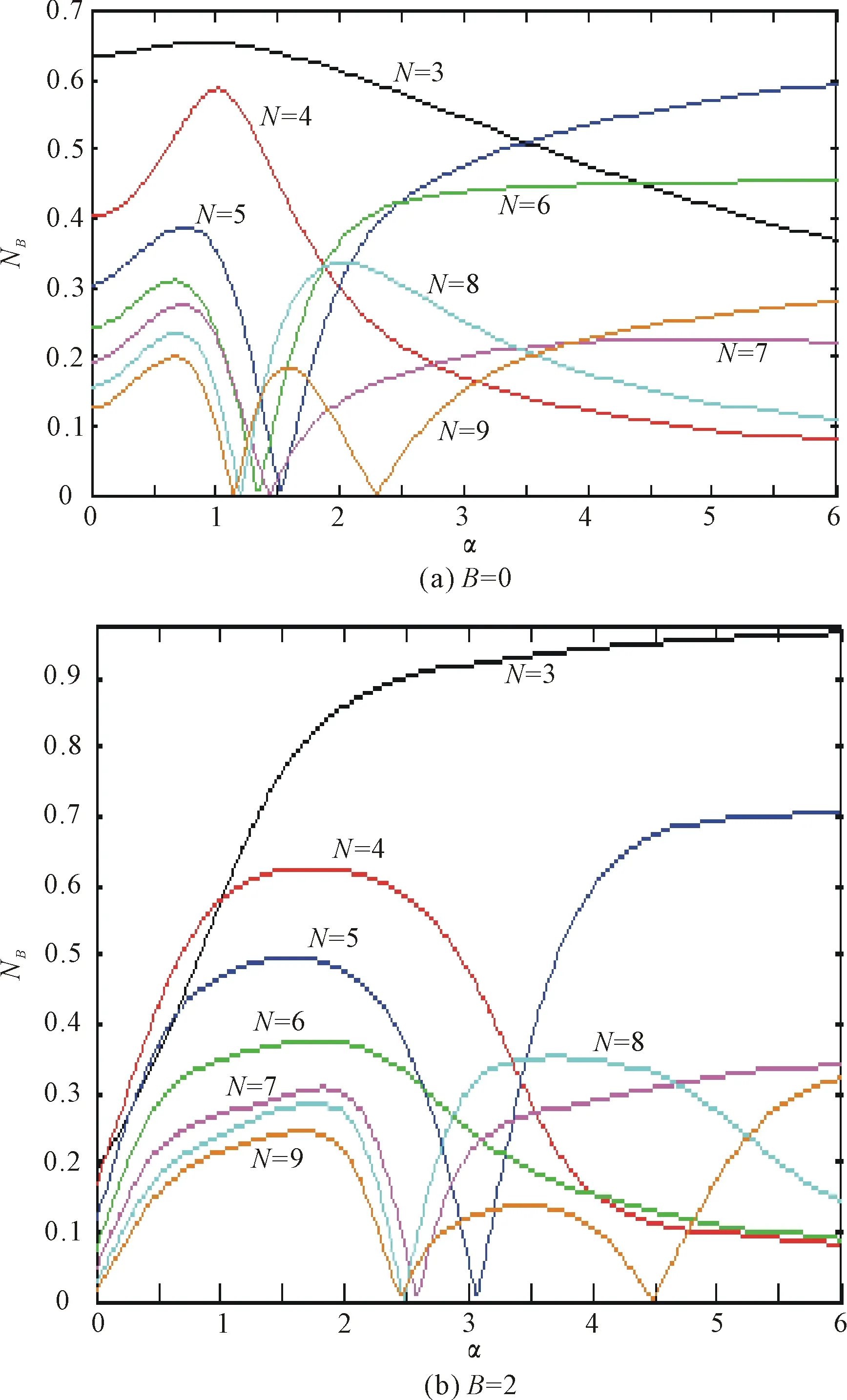
圖1　NB(ρ1N)對XZX+YZY型三體

當給所考察的系統沿z軸方向加上勻強磁場后，其邊界量子比特之間的Bures距離MIN對α的依賴關系會發生較大的變化。如圖1所示，對三量子比特的特殊情形，NB(ρ1N)隨α的增大而單調的增加，并最終趨向一穩態平衡值。而當量子比特數大于等于4時，隨著三體相互作用強度的變大，NB(ρ1N)在定性上表現出和B=0時類似的行為。通過比較圖1中的各條曲線，可以發現當給系統加上勻強外磁場時，雖然在三體相互作用較弱的區間內，其非局域性會有所減弱，但是隨著α的增大，NB(ρ1N)會得到明顯的提高，也即XZX+YZY型三體相互作用和外加磁場的最優結合，可以用來有效調控系統邊界量子比特間測量誘導非局域性的大小。

再考察XZY-YZX型三體相互作用對系統邊界量子比特非局域性大小的影響，數值模擬結果見圖2，其中系統參數kBT=0.5。沒有外磁場時，NB(ρ1N)表現出和XZX+YZY型三體相互作用情形完全不同的變化趨勢。對一般量子比特數的熱平衡態，在弱三體相互作用區間內，隨著作用強度β的增大，NB(ρ1N)先是衰減至某一最小值，只不過對應的臨界βc值并不再是量子比特數的單調函數。之后，隨著β的進一步增大，除三量子比特情形NB(ρ1N)漸進的趨近于其穩態平衡值，對其他情形NB(ρ1N)會出現多個不同的峰值，但是幅度都不是很大。當三體相互作用的強度足夠大時，對五、六和九量子比特的熱平衡態，NB(ρ1N)會漸進的增大至其穩態平衡值，而對四、七和八量子比特情形，NB(ρ1N)則緩慢地衰減至其最小值。另外，通過比較不同數目量子比特的情形，還可以發現通過引入XZY-YZX型三體相互作用，NB(ρ1N)總是會得到某種程度的改善，當然不同數目量子比特態所需要的最佳三體相互作用強度是不同的。

圖2　NB(ρ1N)對XZY-YZX型三體

若給系統加上沿z軸方向的勻強外磁場，則從圖2可以發現，對應的Bures距離MIN轉而表現出和含XZX+YZY型三體相互作用情形非常類似的變化趨勢，即對三量子比特態，NB(ρ1N)隨著β的增強而單調的遞增至其穩態平衡值。對于一般數目量子比特態的情形，在XZY-YZX型三體相互作用較弱的區間內，引進外磁場還是會降低對應Bures距離MIN的值，但是當逐漸增大三體相互作用強度β的值時，NB(ρ1N)又會比沒有外加磁場時變得更大，增大的幅度約為1.5倍。這意味著通過優化所加XZY-YZX型三體相互作用和外加勻強磁場的強度，對應的測量誘導非局域性仍可以得到較為明顯的改善。

3結語

利用Bures距離MIN研究了含XZX+YZY和XZY-YZX兩種不同類型三體相互作用海森堡XX模型的非局域性。通過對不同量子比特數和不同外加磁場強度下Bures距離MIN對三體相互作用強度依賴關系的分析，發現對有限溫度的熱平衡態，XZX+YZY型三體相互作用可用來有效提高系統邊界量子比特之間的非局域性大小，若進一步給系統加上沿z軸方向的勻強磁場，則非局域性的提高會變得更加明顯。對于XZY-YZX型的三體相互作用，雖然在作用強度較弱的區間內，邊界量子比特之間的非局域性會有所減小，但是若適當增大三體相互作用的強度或通過和外加磁場的優化結合，對應的非局域性仍可以得到明顯的增強。這些結果表明對于自旋鏈模型，三體相互作用可以作為一種有效的測量誘導非局域性調控手段。

參考文獻

[1]HORODECKIR,HORODECKIP,HORODECKIM,etal.Quantumentanglement[J/OL].ReviewsofModernPhysics, 2009, 81(2): 865-942[2016-01-11].http://dx.doi.org/10.1103/RevModPhys.81.865.

[2]MODIK,BRODUTCHA,CABLEH,etal.Theclassical-quantumboundaryforcorrelations:discordandrelatedmeasures[J/OL].ReviewsofModernPhysics, 2012, 84(4): 1655-1707[2016-01-11].http://dx.doi.org/10.1103/RevModPhys.84.1655.

[3]EINSTEINA,PODOLSKYB,ROSENN.Canquantum-mechanicaldescriptionofphysicalrealitybeconsideredcomplete[J/OL].PhysicalReview, 1935, 47(10): 777-780[2016-01-11].http://dx.doi.org/10.1103/PhysRev.47.777.

[4]CLAUSERJF,HORNEMA,SHIMONYA,etal.Proposedexperimenttotestlocalhidden-variabletheories[J/OL].PhysicalReviewLetters, 1969, 23(15): 880-883[2016-01-11].http://dx.doi.org/10.1103/PhysRevLett.23.880.

[5]GENOVESEM.Researchonhiddenvariabletheories:areviewofrecentprogresses[J/OL].PhysicsReports, 2005, 413(6): 319-396[2016-01-11].http://dx.doi.org/10.1016/j.physrep.2005.03.003.

[6]WERNERRF.QuantumstateswithEinstein-Podolsky-Rosencorrelationsadmittingahidden-variablemodel[J/OL].PhysicalReviewA, 1989, 40(8): 4277-4281[2016-01-11].http://dx.doi.org/10.1103/PhysRevA.40.4277.

[7]WALGATEJ,HARDYL.Nonlocality,asymmetry,anddistinguishingbipartitestate[J/OL].PhysicalReviewLetters, 2002, 89(14): 147901[2016-01-11].http://dx.doi.org/10.1103/PhysRevLett.89.147901.

[8]LUOSL,FUSS.Measurement-inducednonlocality[J/OL].PhysicalReviewLetters, 2011, 106(12): 120401[2016-01-11].http://dx.doi.org/10.1103/PhysRevLett.106.120401.

[9]GUOY.Measurement-inducednonlocalityovertwo-sidedprojectivemeasurements[J/OL].InternationalJournalofModernPhysicsB, 2013, 27(16): 1350067[2016-01-11].http://dx.doi.org/10.1142/S0217979213500677.

[10]HUML,FANH.Dynamicsofentropicmeasurement-inducednonlocalityinstructuredreservoirs[J/OL].AnnalsofPhysics, 2012, 327(9): 2343-2353[2016-01-11].http://dx.doi.org/10.1016/j.aop.2012.04.003.

[11]HUML,FANH.Measurement-inducednonlocalitybasedonthetracenorm[J/OL].NewJournalofPhysics, 2015, 17(3): 033004[2016-01-11].http://dx.doi.org/10.1088/1367-2630/17/3/033004.

[12]TIANZH,JINGJL.Measurement-inducednonlocalityviatheUnruheffect[J/OL].AnnalsofPhysics, 2013, 333: 76-89[2016-01-11].http://dx.doi.org/10.1016/j.aop.2013.02.001.

[13]SENA,SARKARD,BHARA.Monogamyofmeasurement-inducednonlocality[J/OL].JournalofPhysicsA, 2012, 45(40): 405306[2016-01-11].http://dx.doi.org/10.1088/1751-8113/45/40/405306.

[14]RANAS,PARASHARP.Geometricdiscordandmeasurement-inducednonlocalityforwellknownboundentangledstates[J/OL].QuantumInformationProcessing, 2013, 12(7): 2523-2534[2016-01-11].http://dx.doi.org/10.1007/s11128-013-0545-5.

[15]ZHANGGF,FANH,JIAL,etal.Dynamicsofgeometricdiscordandmeasurement-inducednonlocalityatfinitetemperature[J/OL].EuropeanPhysicalJournalD, 2012, 66(2): 34[2016-01-11].http://dx.doi.org/10.1140/epjd/e2011-20463-x.

[16]RAMZANM.Decoherencedynamicsofgeometricmeasureofquantumdiscordandmeasurementinducednonlocalityfornoninertialobserversatfinitetemperature[J/OL].QuantumInformationProcessing, 2013, 12(8): 2721-2738[2016-01-11].http://dx.doi.org/10.1007/s11128-013-0558-0.

[17]SENA,SARKARD,BHARA.Decoherencedynamicsofmeasurement-inducednonlocalityandcomparisonwithgeometricdiscordfortwoqubitsystems[J/OL].QuantumInformationProcessing, 2013, 12(9): 3007-3022[2016-01-11].http://dx.doi.org/10.1007/s11128-013-0579-8.

[18]PACHOSJK,PLENIOMB.Three-SpinInteractionsinOpticalLatticesandCriticalityinClusterHamiltonians[J/OL].PhysicalReviewLetters, 2004, 93(5): 056402[2016-01-11].http://dx.doi.org/10.1103/PhysRevLett.93.056402.

[19]SHICH,WUYZ,LIZY.Effectsofthree-bodyinteractionsonthedynamicsofentanglementinspinchains[J/OL].PhysicsLettersA, 2009, 373(32): 2820-2823[2016-01-11].http://dx.doi.org/10.1016/j.physleta.2009.06.012.

[20]LIYC,LINHQ.ThermalquantumandclassicalcorrelationsandentanglementintheXYspinmodelwiththree-spininteraction[J/OL].PhysicalReviewA, 2011, 83(5): 052323[2016-01-11].http://dx.doi.org/10.1103/PhysRevA.83.052323.

[責任編輯:瑞金]

Measurement-inducednonlocalityintheXXmodelwiththree-siteinteractions

XIEYuxia,LIUJing

(SchoolofScience,Xi’anUniversityofPostsandTelecommunications,Xi’an710121,China)

Abstract:Nonlocal properties of the Heisenberg XX model with three-site interactions is investigated by using the concept of Bures distance measurement-induced nonlocality (MIN), where more attention is paid on the identification of valid system parameters which can be used for enhancing nonlocality of the boundary qubits. For thermal states of the considered system at finite temperature, the Bures MIN can be enhanced evidently by optimizing strengths of the XZX+YZY or XZY-YZX type three-site interactions and the external magnetic fields. This finding provides a feasible way for tuning nonlocality in the quantum spin system.

Keywords:measurement-induced nonlocality, Heisenberg XX model, three-site interaction

doi:10.13682/j.issn.2095-6533.2016.03.016

收稿日期：2016-04-13

基金項目：陜西省自然科學基礎研究計劃資助項目(2014JM1008)

作者簡介：謝玉霞(1980-)，女，碩士，助教，從事量子通信理論研究。E-mail: yuxia1124@163.com 劉晶(1980-)，女，碩士，講師，研究方向為數值計算。E-mail: xingxin909@126.com

中圖分類號：O431;TN918

文獻標識碼：A

文章編號：2095-6533(2016)03-0094-05