基于剪切波的變分圖像放大方法

王　鵬，吳玉蓮

(1.中航工業西安航空計算技術研究所 13室，陜西 西安 710065；2.西安醫學院 衛生管理系，陜西 西安 710021)

基于剪切波的變分圖像放大方法

王鵬1，吳玉蓮2

(1.中航工業西安航空計算技術研究所 13室，陜西 西安 710065；2.西安醫學院 衛生管理系，陜西 西安 710021)

摘要針對圖像放大的Chambolle 變分模型會出現階梯效應的現象， 文中提出了一種基于Shearlet光滑分解空間的變分模型。利用有界變差空間和Shearlet分解空間的關系，特別是Shearlet分解空間的半范與加權Shearlet系數之間的等價關系,將所求的變分問題轉化為基于Shearlet域的變分問題,其解歸結于簡單的Shearlet閾值。實驗仿真表明，該方法放大后的圖像有效地消除了階梯塊效應，保持了更多的細節，具有更高的峰值信噪比。

關鍵詞圖像放大；剪切波; 變分模型；分解空間

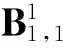
1基礎知識

1.1Shearlet變換

剪切波可利用仿射系統理論將幾何和多尺度分析結合起來的方法構造。當維數n=2時，具有合成膨脹的仿射系統為

SAB(ψ)={ψj,l,k(x)=|detA|j/2ψ(BlAj-k):

j,l∈Z,k∈Z2}

(1)

其中,ψ∈L2(R2),A和B是2×2可逆矩陣,|detB|=1。若SAB(ψ)具有緊框架,則SAB(ψ)的元素成為合成小波。其中Aj與尺度相關聯,Bl與保持面積不變的幾何相關聯

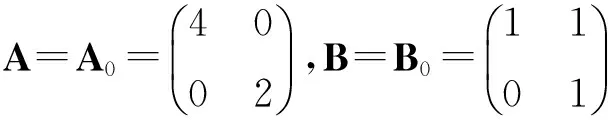
1.2Chambolle圖像放大模型

若討論的圖像是M×N的二維矩陣,X表示空間CM×N,Z是X的一個子空間,g∈Z表示一幅粗糙的低分辨圖像。比如,當放大2倍數時,Z表示為

Z={g∈X|g2k,2l=g2k-1,2l=g2k,2l-1=g2k-1,2l-1,

k≤M/2,l≤N/2}

Chambolle[4]的圖像放大模型為

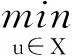
(2)

其中，u是放大后的圖像；A是在空間Z上的正交投影。顯然有Ag=g且

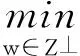
(3)

因此，Chambolle圖像放大模型變為

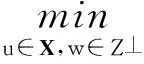
(4)

針對上述最小值問題，Chambolle給出了一種求解的迭代算法,該方法盡管能得到較好的圖像放大效果；但由于此方法是基于TV的方法，所以最后處理結果有階梯塊效應，并不能保持更多的細節信息。……