靜電效應(yīng)對有無埋管氣固鼓泡床內(nèi)氣泡特性的影響分析
吳迎亞,彭麗,藍興英,高金森(中國石油大學(北京)重質(zhì)油國家重點實驗室,北京 102200)
?
靜電效應(yīng)對有無埋管氣固鼓泡床內(nèi)氣泡特性的影響分析
吳迎亞,彭麗,藍興英,高金森
(中國石油大學(北京)重質(zhì)油國家重點實驗室,北京 102200)
摘要:采用基于雙流體模型(TFM)耦合靜電模型的方法,研究顆粒的靜電對有無埋管氣固鼓泡床內(nèi)氣固流動特性和氣泡特性的影響。首先在無靜電場存在的條件下,利用雙流體模型對自由鼓泡床和埋管鼓泡床內(nèi)的流動情況進行模擬并與實驗結(jié)果進行對比;進一步耦合靜電模型,考察靜電對自由鼓泡床和埋管鼓泡床內(nèi)床層的整體性質(zhì)和氣泡特性的影響。研究結(jié)果表明,在無靜電場條件下采用雙流體模型能較好地預(yù)測自由鼓泡床和埋管鼓泡床內(nèi)的氣固流動狀況以及氣泡的平均直徑和氣泡的上升速度。埋管的存在使鼓泡床內(nèi)氣固流動發(fā)生強烈擾動,并使氣泡的平均直徑和氣泡的上升速度均呈振蕩分布。靜電的存在對自由鼓泡床和埋管鼓泡床內(nèi)床層的平均固含率影響不大,但對氣泡分布規(guī)律影響較大,使得自由鼓泡床內(nèi)氣泡數(shù)目減少,而埋管鼓泡床下部區(qū)域的氣泡分布比較集中,上部有大氣泡出現(xiàn)。
關(guān)鍵詞:鼓泡床;流動;計算流體力學;雙流體模型;靜電效應(yīng);氣泡特性;模擬
2015-09-06收到初稿,2015-11-16收到修改稿。
聯(lián)系人:藍興英。第一作者:吳迎亞(1990—),男,博士研究生。
Received date: 2015-09-06.
Foundation item: supported by the National Natural Science Foundation of China (91334104) and the New Century Excellent Talents Program in University (NCET-13-1027).
ids bubbling bed with the immersed horizontal tubes.
引 言
鼓泡床具有良好的傳熱和傳質(zhì)特點,在化學工程、生物環(huán)境工程以及食品加工方面有著廣泛的應(yīng)用[1]。而在氣固鼓泡床中,由于顆粒間及顆粒與壁面的摩擦和碰撞將產(chǎn)生不可忽略的靜電效應(yīng)[2]。靜電的廣泛存在對氣固鼓泡床的流動產(chǎn)生顯著的影響,其存在可能會對工業(yè)尺寸的流化床造成安全事故,輕則導(dǎo)致流化失常,重則導(dǎo)致反應(yīng)器停車甚至放電爆炸等[3]。如何準確地預(yù)測靜電的存在對氣固鼓泡床內(nèi)流動特性,尤其是對氣泡特性的影響,是預(yù)防靜電在氣固鼓泡床內(nèi)產(chǎn)生影響的關(guān)鍵[4]。
在工業(yè)氣固鼓泡床內(nèi)氣泡形狀大小各異和氣泡上升運動是造成顆粒和氣體返混的主要原因,氣泡的生成、聚并以及破碎決定了氣固鼓泡床的傳熱和反應(yīng)效率,因此氣泡的存在對床層傳遞和反應(yīng)特性方面有著重要影響[5]。Sitnai等[6]和Hull等[7-8]指出氣固鼓泡床內(nèi)埋管的存在對其流動特性和氣泡分布有較大的影響。Boland等[9]首次闡述了流化床中靜電產(chǎn)生的機理。Chen等[10]通過實驗手段研究了靜電的存在對流化床內(nèi)流動特性的影響。Dong等[11]也通過實驗手段研究了鼓泡床內(nèi)顆粒的靜電對流化床內(nèi)流動特性及氣泡行為的影響。Rokkam等[12]采用基于歐拉雙流體模型耦合靜電模型的方法研究了靜電的存在對氣固鼓泡床內(nèi)流動特性的影響,但并未研究靜電的存在對鼓泡床內(nèi)氣泡特性的影響。Jalalinejad等[13]研究了靜電對流化床內(nèi)單個氣泡的影響,模擬結(jié)果顯示靜電效應(yīng)的存在導(dǎo)致氣泡伸長,并且隨電荷增強氣泡伸長更加明顯。Sun等[14]研究了靜電的存在對自由鼓泡床內(nèi)氣泡特性的影響。Pei 等[15]采用DEM-CFD方法研究了不同靜電力模型對顆粒運動規(guī)律的影響。Hassani等[16]利用DEM-CFD方法考察了靜電的存在對鼓泡床內(nèi)氣固流動特性的影響。這些研究都說明在氣固流化床中靜電的存在影響了整個床層內(nèi)的氣固流動特性和氣泡的運動特性。但目前通過模擬手段研究靜電的存在對埋管鼓泡床內(nèi)氣固流動特性和氣泡特性的影響鮮有報道。
本研究采用基于歐拉雙流體模型耦合靜電模型的方法,分別模擬有無埋管存在的二維鼓泡流化床內(nèi)的氣固流動狀況,重點研究了靜電的存在對自由鼓泡床和埋管鼓泡床內(nèi)床層的平均固含率分布和氣泡的分布特性的影響。
1 模擬對象
本研究的模擬工況為Asegehegn等[17]的擬二維有無埋管的鼓泡床冷態(tài)實驗,計算模型如圖1所示。計算入口處采用從氣體底部均勻進氣,無顆粒進入,無分布板;氣體出口采用壓力出口。具體的實驗條件及相關(guān)模擬參數(shù)見表1。
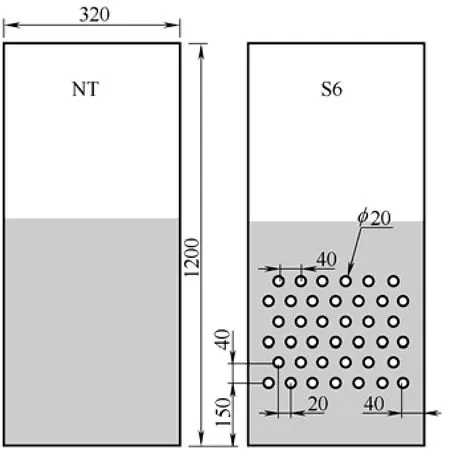
圖1 計算模型的幾何結(jié)構(gòu)Fig. 1 Geometry structure of simulation domain
2 數(shù)學模型
本研究采用Fluent 6.3.2軟件,基于雙流體模型(TFM),結(jié)合顆粒動力學理論(KTGF),耦合靜電模型,對二維鼓泡床內(nèi)氣固流動過程進行模擬研究。
2.1雙流體模型
雙流體模型關(guān)系式和參數(shù)在很多文獻中都有報道,其氣相和顆粒相的守恒方程如下[18]
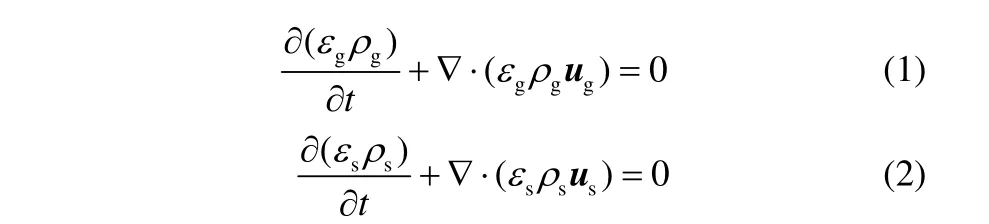
體積分數(shù)之間的關(guān)系如下

氣相和顆粒相的動量守恒方程表達式如下

表1 模擬條件Table 1 Simulation conditions
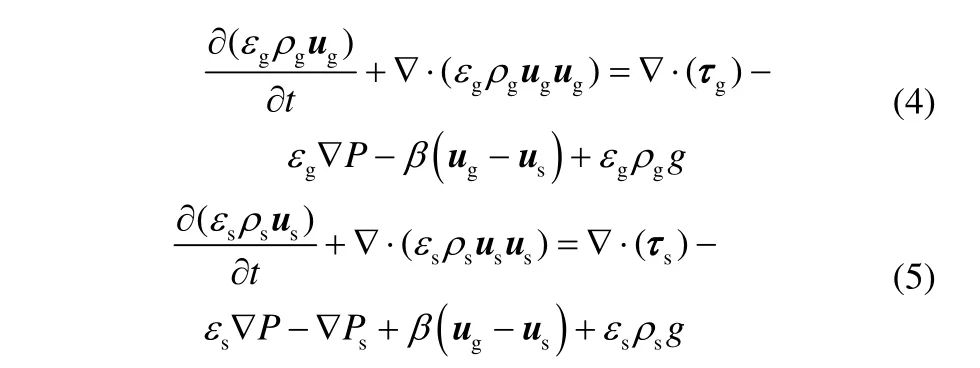
其中顆粒相性質(zhì)由顆粒動理學理論描述[19]。
在動量守恒方程中最重要的封閉方程是氣體和顆粒相間的曳力作用,曳力采用O’Brien和Syamlal曳力模型[20],如式(6)~式(8)所示

式中,Re為Reynolds數(shù)。
2.2靜電模型
采用麥克斯韋方程描述靜電場[21]。
麥克斯韋方程共包括4個不同的偏微分方程,如下所示
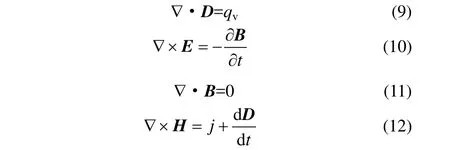
其中
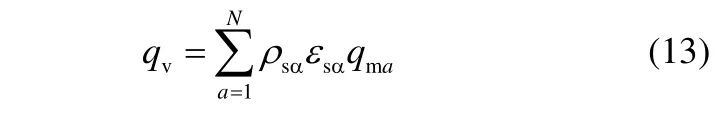
式中D,qv,qm,H,j,t分別代表電位移、體電荷密度、荷質(zhì)比、磁場強度、電流密度和時間。
在流化床內(nèi),由自身電場變化產(chǎn)生的磁場對流動影響較小,一般可以忽略。則法拉第定律轉(zhuǎn)化為

得到

則顆粒在電場中的受力描述如下

得到電位移和電場強度的關(guān)系為

式中,x0為真空介電常數(shù),P為電極化強度。假設(shè)流化床內(nèi)存在各向同性的電介質(zhì),則

則

式中,xm為電介質(zhì)的相對介電常數(shù)。所以
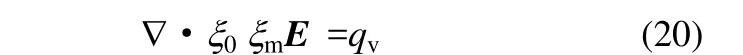
如文獻[12] 中所述,氣固混合物的相對介電常數(shù)為相體積分數(shù)的函數(shù),進一步得到電場的基本方程[12-13]如下

最后得到帶電顆粒自身產(chǎn)生的靜電力如下
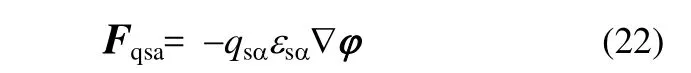
2.3耦合方法
根據(jù)以上推導(dǎo)的靜電模型[如式(22)],采用Fluent
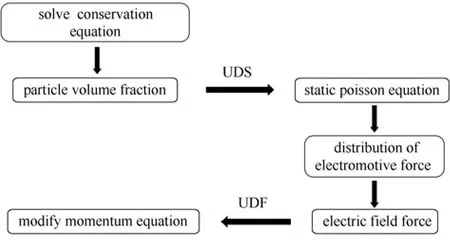
圖2 雙流體模型耦合靜電模型算法Fig. 2 Two-fluid model coupling with electrostatic model
6.3.2中提供的UDS和UDF耦合靜電模型與雙流體模型[12]。其耦合過程如圖2所示。
步驟為:① 首先求解雙流體模型,得到每個網(wǎng)格的氣相體積分數(shù)和固相分數(shù);② 通過UDS求解電場的泊松方程,得到電勢的分布;③ 根據(jù)電場的分布計算靜電力;④ 耦合靜電力,通過UDF修正動量方程。

圖3 鼓泡床內(nèi)瞬時氣含率全床分布云圖(t=5.0 s)Fig. 3 Instantaneous contours of gas volume fraction for bubbling bed (t=5.0 s)
3 分析和討論
3.1模型驗證
在氣固鼓泡床內(nèi)氣泡的尺寸和運動決定了氣固鼓泡床內(nèi)的傳熱和傳質(zhì)效率,研究氣固鼓泡床內(nèi)氣泡的詳細特征能為鼓泡床反應(yīng)器的設(shè)計和放大、改善反應(yīng)器的操作狀況提供一定的依據(jù)。通過每個網(wǎng)格的空隙率定義氣泡,一般氣泡空隙率閾值定義為0.8[22]。利用MATLAB圖形工具箱,采用逐幀分析方法確定氣泡的相對位置和運動速度,進一步得到氣泡的分布信息和氣泡的運動信息。
本研究首先利用雙流體模型研究了無靜電場存在下的自由氣固鼓泡床和埋管鼓泡床內(nèi)的氣固流動狀況以及氣泡的特性,并與Asegehegn等[17]的實驗結(jié)果進行對比。圖3為自由鼓泡床和埋管鼓泡床的瞬時氣含率全床分布云圖。由圖3可知,與自由鼓泡床內(nèi)氣泡的大小和分布相比,在埋管鼓泡床內(nèi),由于埋管的存在,埋管區(qū)域處的氣泡被埋管打碎,氣泡數(shù)目變多、平均直徑變小。圖4和圖5分別對比了自由鼓泡床和埋管鼓泡床內(nèi)氣泡的平均直徑的軸向分布以及氣泡平均上升速度的軸向分布的實驗結(jié)果和模擬結(jié)果。由圖4和圖5可知,隨著自由氣固鼓泡床和埋管鼓泡床床層高度的增加,氣泡的平均直徑和氣泡的平均上升速度逐漸增大。但埋管的存在對氣泡特性影響較大,主要原因是,一方面在埋管鼓泡床內(nèi)氣泡的平均直徑和氣泡的平均上升速度均低于自由管鼓泡床內(nèi)氣泡的平均直徑和氣泡的平均上升速度,另一方面埋管的存在使得鼓泡床內(nèi)的氣固流動發(fā)生強烈的擾動,氣泡的平均直徑和氣泡的平均上升速度均呈振蕩分布。而在自由鼓泡床和埋管鼓泡床床層界面處,氣泡的平均直徑和氣泡的平均上升速度的模擬結(jié)果均與實驗結(jié)果相差較大,這可能是由于在模擬和實驗過程中對界面處的氣泡的統(tǒng)計方法不同導(dǎo)致。模擬計算結(jié)果與實驗結(jié)果的對比表明,采用雙流體模型能較好地預(yù)測無靜電場存在下的自由鼓泡床和埋管鼓泡床內(nèi)的氣固流動狀況和氣泡的平均直徑以及氣泡的平均上升速度。
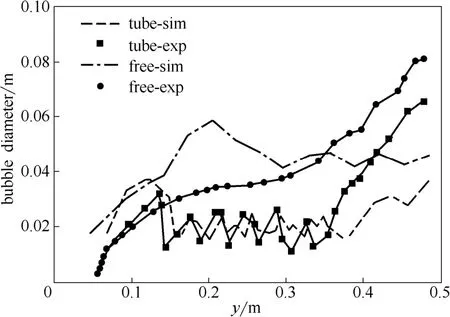
圖4 自由鼓泡床和埋管鼓泡床內(nèi)氣泡的平均直徑的軸向分布Fig. 4 Axial profile of bubble diameter for free bubbling bed and tube-immersed bubbling bed
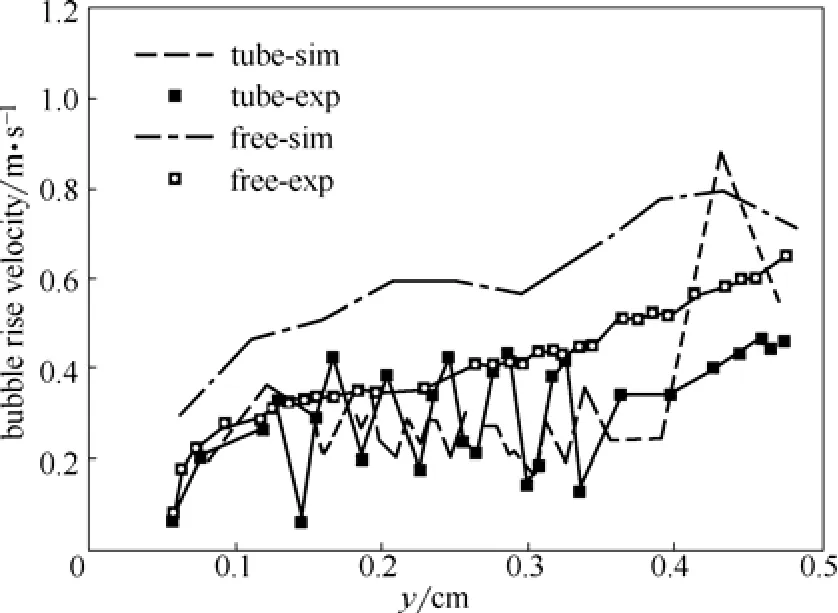
圖5 自由鼓泡床和埋管鼓泡床內(nèi)氣泡的平均上升速度的軸向分布Fig. 5 Axial profile of bubble riser velocity for free bubbling bed and tube-immersed bubbling bed
3.2靜電的存在對自由鼓泡床和埋管鼓泡床整體特性的影響
氣固鼓泡床內(nèi)靜電產(chǎn)生的原因主要是顆粒、反應(yīng)器壁面以及氣體之間的碰撞和摩擦使顆粒帶電。正是由于顆粒的帶電和極化才使得床層中存在靜電場,而靜電場的存在影響床層內(nèi)顆粒的混合和流動,從而影響鼓泡床內(nèi)氣固流動特性和氣泡的分布特性。Sowinski等[22]通過分別測量流化床內(nèi)3個重點區(qū)域處顆粒(床內(nèi)顆粒、粘壁顆粒和夾帶顆粒)所帶的電荷量研究流化床內(nèi)靜電的分布。實驗結(jié)果發(fā)現(xiàn),在鼓泡床流化穩(wěn)定后,床內(nèi)顆粒主要帶負電。本體系中顆粒的帶電取值為-0.0025 C·m-3。
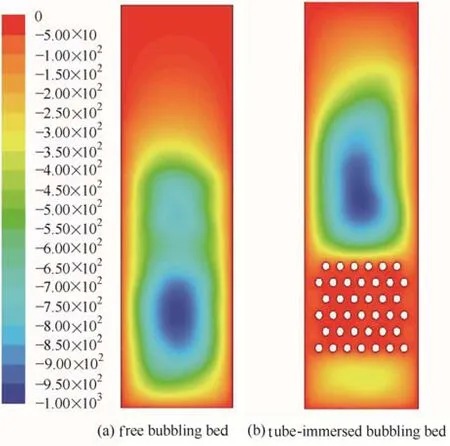
圖6 鼓泡床內(nèi)瞬時電動勢分布云圖(t=5.0 s)Fig. 6 Contours of instantaneous electric potential from bubbling bed simulations (t=5.0 s)

圖7 自由鼓泡床和埋管鼓泡床內(nèi)平均固含率的軸向分布Fig. 7 Axial profile of time-averaged solids holdup for bubbling bed with and without electrostatic

圖8 自由鼓泡床內(nèi)瞬時氣含率全床分布云圖(t=5.0 s)Fig. 8 Instantaneous contours of gas volume fraction for free bubbling bed (t=5.0 s)

圖9 埋管鼓泡床內(nèi)瞬時氣含率全床分布云圖(t=5.0 s)Fig. 9 Instantaneous contours of gas volume fraction for tube-immersed bubbling bed with and without electrostatic (t=5.0 s)
流化床內(nèi)靜電場的分布情況是靜電的宏觀表現(xiàn)。靜電分布可以通過兩方面表征:一方面是直接測量顆粒的電荷量分布,但該方法往往難于在線測量電荷量;另一方面是通過測量流化床內(nèi)電動勢或電流分布反映流化床內(nèi)的靜電分布規(guī)律[23]。本研究通過雙流體模型耦合靜電模型模擬靜電場的存在對鼓泡床內(nèi)氣固流動狀況的影響。圖6是鼓泡床床層穩(wěn)定后的瞬時電動勢分布云圖。由圖6可知,由于埋管的存在,埋管鼓泡床內(nèi)埋管區(qū)域的上部和下部均存在一個梯度較大的電動勢分布。進一步統(tǒng)計了自由鼓泡床和埋管鼓泡床在有無靜電場存在下的平均固含率的軸向分布,如圖7所示。由圖7可知,自由鼓泡床和埋管鼓泡床內(nèi)平均固含率在有無靜電場存在下變化不大,說明靜電場的存在對自由鼓泡床和埋管鼓泡床床層的平均性質(zhì)影響不大。
3.3靜電的存在對自由鼓泡床和埋管鼓泡床內(nèi)氣
泡特性的影響
氣泡在鼓泡床中扮演了極其重要的作用,氣泡的生成、聚并以及破碎決定了氣固鼓泡床的傳熱和反應(yīng)效率,因此分析靜電的存在對氣泡特性的影響意義重大。
圖8和圖9給出了自由鼓泡床和埋管鼓泡床在有無靜電場存在下的瞬時氣含率分布云圖。由圖8和圖9可知,靜電場的存在對自由鼓泡床和埋管鼓泡床床層的瞬時氣固流動狀況和氣泡的瞬時分布狀況(氣泡的大小和位置)均有一定的影響,在有靜電場存在的自由鼓泡床床層內(nèi)氣泡數(shù)目減少,而在埋管鼓泡床床層下部區(qū)域處氣泡分布比較集中,同時較大氣泡出現(xiàn)在床層上部區(qū)域。
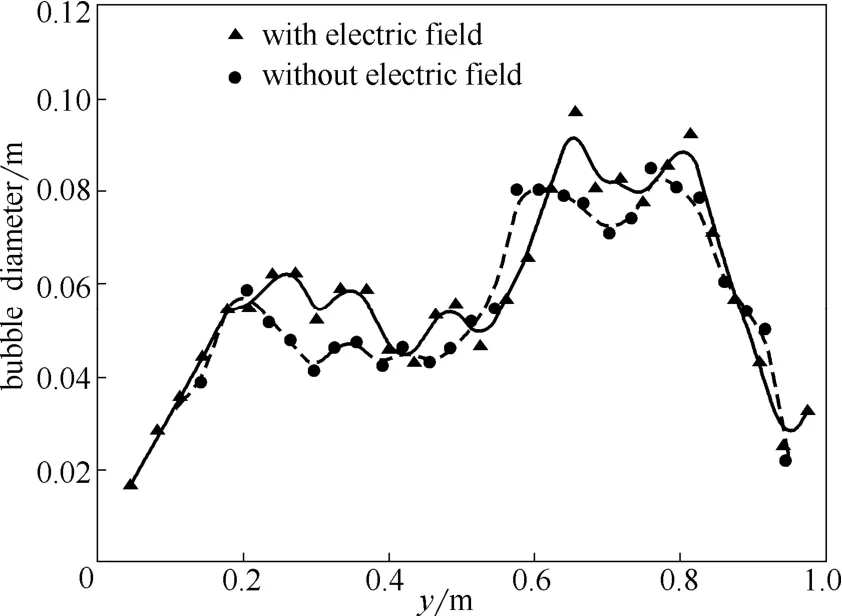
圖10 自由鼓泡床內(nèi)氣泡的平均直徑的軸向分布Fig. 10 Axial profile of bubble diameter for free bubbling bed with and without electrostatic
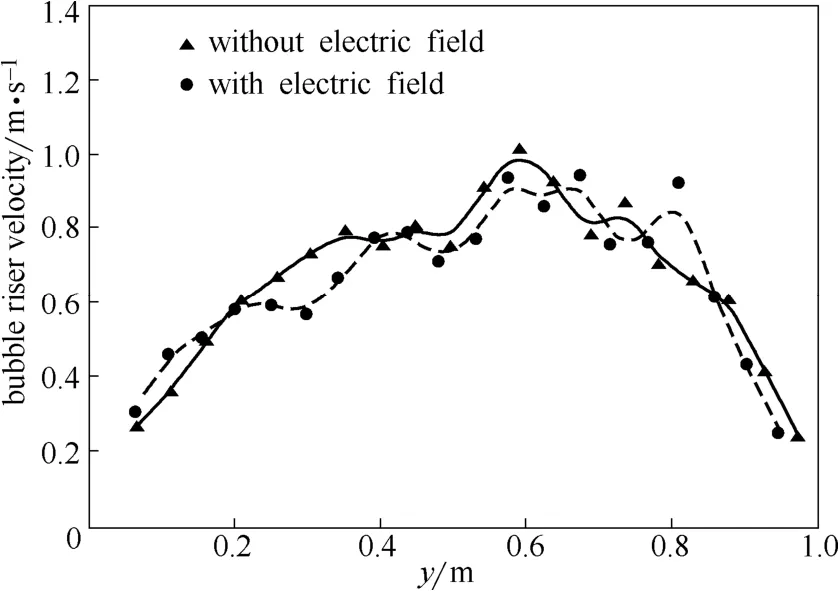
圖11 自由鼓泡床內(nèi)氣泡的平均上升速度的軸向分布Fig. 11 Axial profile of bubble riser velocity for free bubbling bed with and without electrostatic
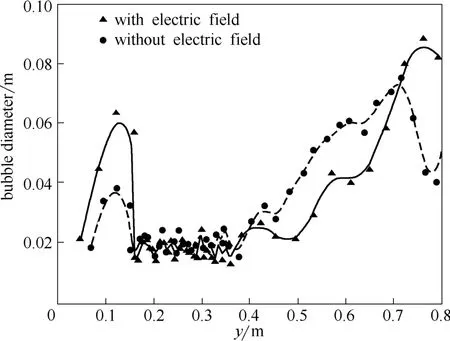
圖12 埋管鼓泡床內(nèi)氣泡的平均直徑的軸向分布Fig. 12 Axial profile of bubble diameter for tube-immersed bubbling bed with and without electrostatic
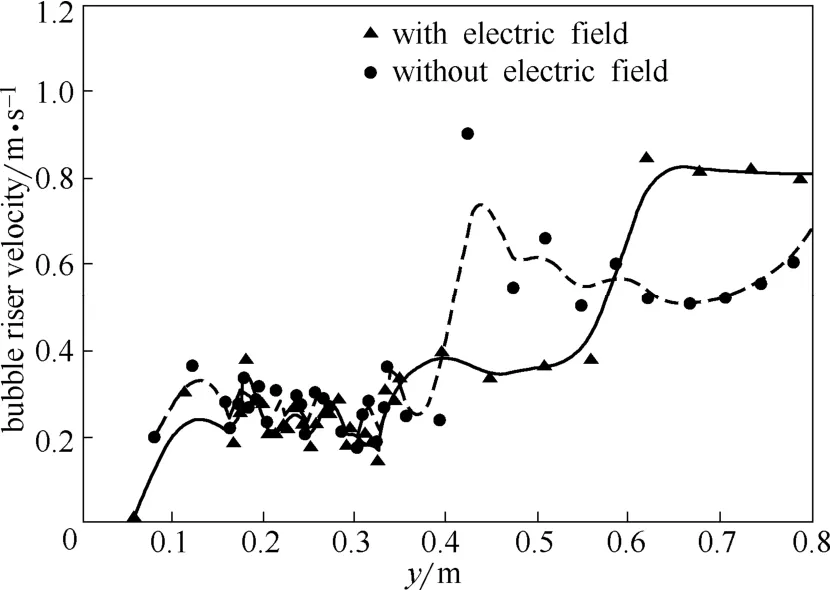
圖13 埋管鼓泡床內(nèi)氣泡的平均上升速度的軸向分布Fig. 13 Axial profile of bubble riser velocity for tube-immersed bubbling bed with and without electrostatic
圖10和圖11分別為有無靜電場存在下自由鼓泡床內(nèi)氣泡的平均直徑和氣泡的平均上升速度的軸向分布。由圖10和圖11可知,自由鼓泡床在床層高度為0.3~0.7 m區(qū)域,氣泡的平均直徑和氣泡的平均上升速度受靜電場影響較大。這是由于在自由鼓泡床床層高度為0.3 m和0.7 m附近電動勢存在極小值(如圖6所示),較大的電動勢梯度使得床層在0.3 m和0.7 m附近存在較強的靜電場。圖12和圖13分別為有無靜電場存在下埋管鼓泡床內(nèi)氣泡的平均直徑和氣泡的平均上升速度的軸向分布。由圖12和圖13可知,靜電場的存在對埋管鼓泡床內(nèi)氣泡的平均直徑和氣泡的平均上升速度的影響更加明顯,這可能是由于床層內(nèi)構(gòu)件埋管的存在使得埋管上部區(qū)域形成了較強的靜電場,對氣泡的平均直徑和氣泡的平均上升速度產(chǎn)生較大的影響。
4 結(jié) 論
本研究采用靜電模型與雙流體模型耦合的方法對氣固鼓泡床內(nèi)的氣固流動特性和氣泡特性進行模擬研究,重點研究了有無靜電場存在下的自由鼓泡床和埋管鼓泡床內(nèi)的氣固流動特性、氣泡的分布規(guī)律、氣泡的平均直徑以及氣泡的平均上升速度,得到以下結(jié)論。
(1)在無靜電場影響下,隨著自由鼓泡床和埋管鼓泡床床層高度的增加,氣泡的平均直徑和氣泡的平均上升速度逐漸增大。埋管的存在使得床內(nèi)氣固流動發(fā)生強烈的擾動,埋管鼓泡床內(nèi)氣泡的平均直徑呈振蕩分布。對比模擬結(jié)果與實驗結(jié)果表明,在無靜電場存在下雙流體模型能較好地預(yù)測自由鼓泡床和埋管鼓泡床內(nèi)氣固的流動狀態(tài)和氣泡的分布規(guī)律。
(2)對比分析自由鼓泡床和埋管鼓泡床在有無靜電場存在下的平均固含率的變化情況發(fā)現(xiàn),靜電場的存在對自由鼓泡床和埋管鼓泡床的整體平均性質(zhì)影響不大。
(3)對比自由鼓泡床和埋管鼓泡床在有無靜電場存在下的氣泡特性的變化情況發(fā)現(xiàn),在自由鼓泡床內(nèi),靜電場的存在使得床內(nèi)氣泡的數(shù)目減少,氣泡的平均直徑和氣泡的上升速度在床層高度為0.3 m和0.7 m附近變化較大;在埋管鼓泡床內(nèi),由于埋管的存在導(dǎo)致埋管上部形成較強的靜電場,從而對氣泡的平均直徑和氣泡的平均上升速度的影響更加明顯。
符號說明
B ——磁感應(yīng)強度
D ——電位移
dp——顆粒半徑
E ——電場強度
F ——電場力
Fqsa——帶電顆粒自身產(chǎn)生的靜電力
g——重力加速度
H——磁場強度
j——電流密度
P——電極化強度
Ps——固相壓力
qm——荷質(zhì)比
qsa——顆粒帶電量
qv——體電荷密度
t——時間
u——速度
x——床層徑向距離
b——曳力
e——空隙率
esa——顆粒固含率
xm——電介質(zhì)的相對介電常數(shù)
x0——真空介電常數(shù)
r——密度
t——應(yīng)力
j——電動勢
下角標
g——氣相
s——固相
References
[1] 金涌,祝京旭,俞芷青.流態(tài)化工程原理[M]. 北京: 清華大學出版社,2001: 72-75. JIN Y,ZHU J X,YU Z Q. Fluidization Engineering Principles[M]. Beijing: Tsinghua University Press,2001: 72-75.
[2] 朱子川,孫婧元,黃正梁,等. 外加電場下氣固流化床的數(shù)值模擬[J]. 化工學報,2013,64(2): 490-497. ZHU Z C,SUN J Y,HUANG Z L,et al. Numerical simulation of gas-solids fluidized bed with applied electric field [J]. CIESC Journal,2013,64(2): 490-497.
[3] HENDRICKSON G. Electrostatics and gas phase fluidized bed polymerization reactor wall sheeting [J]. Chemical Engineering Science,2006,61(4): 1041-1064.
[4] 王芳,徐怡,于恒修,等. 氣固流化床中靜電壓分布及料位檢測[J]. 化工學報,2008,59(3): 574-581. WANG F,XU Y,YU H X,et al. Electrostatic potential distribution in gas-solid fluidized beds and measurement of bed level [J]. Journal of Chemical Industry and Engineering(China),2008,59(3): 574-581.
[5] CANO-PLEITE E,HEMANDEZ-JIMENEZ F,DE V M,et al. Experimental study on the motion of isolated bubbles in a vertically vibrated fluidized bed [J]. Chemical Engineering Journal,2014,255: 114-125.
[6] SITNAI O,WHITEHEAD A B. Immersed tubes and other internals[M]//Fluidization. London: Academic Press,1985: 473-493.
[7] HULL A S,CHEN Z,F(xiàn)RITZ J W,et al. Influence of horizontal tubebanks on the behavior of bubbling fluidized beds(1): Bubble hydrodynamics [J]. Powder Technology,1999,103(3): 230-242
[8] HULL A S,CHEN Z,AGARWAL P K. Influence of horizontal tube banks on the behavior of bubbling fluidized beds(2): Mixing of solids [J]. Powder Technology,2000,111(3): 192-199.
[9] BOLAND D,GELDART D. Electrostatic charging in gas fluidised beds [J]. Powder Technology,1972,5(5): 289-297.
[10] CHEN A H,BI H T,GRACE J R. Measurement of particle charge-to-mass ratios in a gas–solids fluidized bed by a collision probe [J]. Powder Technology,2003,135: 181-191.
[11] DONG K,ZHANG Q,HUANG Z,et al. Experimental investigation of electrostatic effect on bubble behaviors in gas-solid fluidized bed [J]. AIChE Journal,2015,61(4): 1160-1171.
[12] ROKKAM R G,SOWINSKI A,F(xiàn)OX R O,et al. Computational and experimental study of electrostatics in gas–solid polymerization fluidized beds [J]. Chemical Engineering Science,2013,92: 146-156. [13] JALALINEJAD F,BI X T,GRACE J R. Effect of electrostatic charges on single bubble in gas–solid fluidized beds [J]. International Journal of Multiphase Flow,2012,44: 15-28.
[14] SUN J,WANG J,YANG Y,et al. Effects of external electric field on bubble and charged particle hydrodynamics in a gas–solid fluidized bed [J]. Advanced Powder Technology,2015,26(2): 563-575.
[15] PEI C,WU C Y,ENGLAND D,et al. DEM-CFD modeling of particle systems with long-range electrostatic interactions [J]. AIChE Journal,2015,61(6): 1792-1803.
[16] HASSANI M A,ZARGHAMI R,NOROUZI H R,et al. Numerical investigation of effect of electrostatic forces on the hydrodynamics of gas–solid fluidized beds [J]. Powder Technology,2013,246: 16-25.
[17] ASEGEHEGN T W,SCHREIBER M,KRAUTZ H J. Investigation of bubble behavior in fluidized beds with and without immersed horizontal tubes using a digital image analysis technique [J]. Powder Technology,2011,210(3): 248-260.
[18] LI T,BENYAHIA S. Evaluation of wall boundary condition parameters for gas–solids fluidized bed simulations [J]. AIChE Journal,2013,59(10): 3624-3632.
[19] GIDASPOW D,LU H L. Collisional viscosity of FCC particles in a CFB [J]. AIChE Journal,1996,42(9): 2503-2510.
[20] O’BRIEN T J,SYAMLAL M. Particle cluster effects in the numerical simulation of a circulating fluidized bed [C]// AVIDAN A. Proceedings of the Fourth International Conference on Circulating Fluidized Beds. Somerset,PA: 1993.
[21] JACKSON J D,F(xiàn)OX R F. Classical electrodynamics [J]. American Journal of Physics,1999,67(9): 841-842.
[22] SOWINSKI A,MILLER L,MEHRANI P. Investigation of electrostatic charge distribution in gas–solid fluidized beds [J]. Chemical Engineering Science,2010,65(9): 2771-2781.
[23] 朱子川. 外加電場下氣固流化床的數(shù)值模擬[D]. 杭州: 浙江大學,2013. ZHU Z C. Numerical simulation of gas-solid fluidized bed with applied electric field[D]. Hangzhou: Zhejiang University,2013.
Effect of electrostatic on bubble hydrodynamics in gas-solids bubbling bed with and without immersed horizontal tubes
WU Yingya,PENG Li,LAN Xingying,GAO Jinsen
(State Key Laboratory of Heavy Oil Processing,China University of Petroleum,Beijing 102200,China)
Key words:bubbling bed; flow; computational fluid dynamics (CFD); two-fluid model; electrostatic effects; bubble hydrodynamics; simulation
Abstract:The present paper studied the effects of electrostatics on gas-solids hydrodynamics and bubble characteristics of gas-solids bubbling bed with and without immersed horizontal tubes by applying the two-fluid model coupling with the electrostatic model. At first,the two-fluid model without electrostatic field was adopted to simulate the hydrodynamics in the gas-solids bubbling bed with and without immersed horizontal tubes. Further coupled with the electrostatic model,the effects of electrostatics on bubble distribution characteristics in the gas-solids bubbling bed with and without the immersed horizontal tubes were investigated. The results demonstrated that in the electrostatic field conditions,the two-fluid model can be used to predict gas-solid flow conditions,the bubble diameter,and bubble riser velocity for gas-solids bubbling bed with and without immersed horizontal tubes. However,the immersed horizontal tubes in gas-solids bubbling bed caused an intense disturbance of gas-solids,making a concussion in the distribution of the bubble diameter and bubble riser velocity. The electrostatics did not have a large effect on the average solids holdup of the bed,but showed a greater impact on the bubble characteristics. The electrostatics decreased the number of bubbles of the gas-solids bubbling bed without the immersed horizontal tubes and made more number of bubbles be concentrated in the lower region ofthe gas-solids bubbling bed with the immersed horizontal tubes and more number of large bubbles be located in the upper part of the gas-sol
DOI:10.11949/j.issn.0438-1157.20151394
中圖分類號:TE 65
文獻標志碼:A
文章編號:0438—1157(2016)04—1150—09
基金項目:國家自然科學基金項目(91334104);教育部新世紀優(yōu)秀人才支持計劃項目(NCET-13-1027)。
Corresponding author:LAN Xingying,lanxy@cup.edu.cn

