任意角的三角函數定義引入的微課教學設計
張軍鋼

設計的意圖:“任意角的三角函數的概念”的教學設計應注意通過與“銳角三角函數”概念的因襲與擴張關系,引導學生參與“定義任意角三角函數的過程”.有了適切的“立意”,借助怎樣的載體來落實,也是一個值得細究的問題.那么,以“銳角三角函數的概念”作為任意角三角函數的知識生長點是否合適?“銳角三角函數的概念”是以直角三角形為載體,關注的是“解決直角三角形的邊角關系問題”,而對它的函數本性的認識并不是重點,銳角三角函數并沒有被納入函數概念體系中.因此,要使銳角三角函數概念成為教學的起點,還需要一個較長的過程鋪墊:回顧定義——坐標化(全新的學習)——“單位化”(取r=1,全新的學習),而且學生可能無法把任意角的三角函數的概念納入到函數的概念中.
因此,還有一種想法是在函數概念下以“圓心在原點的圓周上的點的坐標”隨角的變化而變化的“操作、觀察”,先讓學生建立起“任意給定一個角α,圓周上就有唯一的一個點P(x,y)與之對應”的直觀感受,把注意力集中在三角函數的“函數特性”上,能使學生認清其對應關系、定義域和值域等,從而真正把握三角函數的“本來面目”.是否可以在“函數是描述客觀世界變化規律的數學模型”的思想指導下,以“如何建立圓周運動的數學模型”為教學起點,調動象限角、弧度制、單位圓、銳角三角函數等相關知識,在建立函數模型的過程中水到渠成地引入任意角三角函數的概念.這樣,既可以使學生知道這一概念的背景、解決的問題,也可以使他們感受運用函數概念建立模型的過程和方法,還可以讓他們體會三角函數在物理學科中的重要性.如果這樣的設計思想能夠實現,那么其效果是一舉多得的.以下為筆者在教學實踐中對任意角的三角函數定義引入的微課設計.
一、教材分析
三角函數是函數的一個基本組成部分,也是一個重要組成部分,在整個高中以至于大學都會經常用到三角函數的知識.初中已經學習過銳角的三角函數,教材第一節學習了任意角的表示方法,這些是學習任意角三角函數的基礎.本節課的主要內容是:正弦、余弦、正切的定義;正弦、余弦、正切函數的定義域.
二、教學目標
理解任意角的三角函數的定義.
三、重點,難點
1.重點:任意角的正弦、余弦、正切的定義;
2.難點:任意角的三角函數概念的建構過程;
四、教學情景設計
1.引 入
我們初中已經學習了銳角三角函數,知道它是以銳角為自變量,
以比值為函數值的函數,那么高中為什么還要繼續研究呢?
實例導入:“離離原上草,一歲一枯榮.野火燒不盡,春風吹又生.”(王安石詩).詩中描繪的是自然界中“按一定規律周而復始”的現象,稱之為“周期現象.”我們曾學習過用“指數函數”模型刻畫人口增長問題,用“對數函數”的模型刻畫地震的震級變化,用怎樣的數學模型來刻畫周期現象呢?“周期現象一般與周期運動有關”,一個簡單而基本的例子便是“圓周上的一點旋轉運動”.
2.探 究
情境——選擇數學模型.
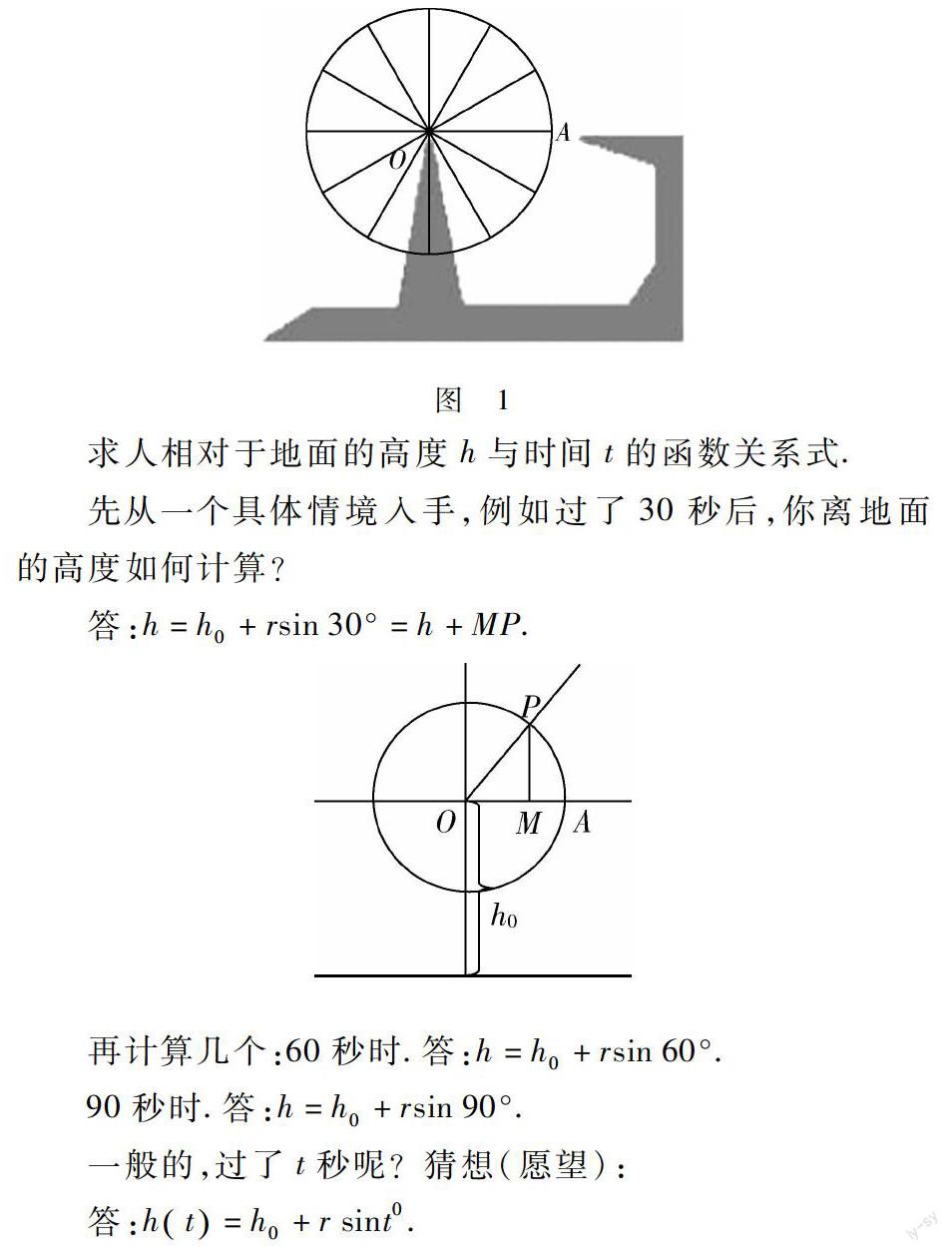
問題:摩天輪的中心離地面高度為h0,它的直徑為2r,逆時針方向勻速轉動,轉動一周需要360秒,若現在你坐在座艙中,從初始位置點A 出發(如圖1所示).
求人相對于地面的高度h與時間t的函數關系式.
先從一個具體情境入手,例如過了30秒后,你離地面的高度如何計算?答:h=h0+rsin30°=h+MP.
再計算幾個:60秒時.答:h=h0+rsin60°.
90秒時.答:h=h0+rsin90°.
一般的,過了t秒呢?猜想(愿望):
答:ht=h0+rsint0.
“這樣的想法合情,但合理嗎?”
(意圖:先從幾個特殊情形出發,而后猜測一般性結論,再進行合理性論證!)
總結:人距離地面的高度h=h0+MP,其中h0是不變量,MP表示點P 到水平位置OA的距離,是變量;可以通過點P旋轉的角度∠POA的大小,再結合初中銳角三角函數來計算.
3.分析數學模型
問題:對任意角∠POA;sin∠POA該如何定義?對前面這個問題往下具體分析:
當時間為t秒時,人距離地面的高度用h=h0±MP來表示,其中MP 表示點P到水平位置OA的距離.
對比:h=h0±MP與ht=h0+rsint0.
愿望:要想兩者和諧統一.
必須有:rsint0=±MP即:sint0=±MP/r.
小結:點P在圓周上旋轉運動,引起∠POA的變化,對任意一個確定的∠POA對應著唯一點P,進而有唯一的MP,得到sin∠POA=±MP/r①.
提問一:①式的分子何時取正值,何時取負值?
答:OA上方為正,OA下方為負.
提問二:根據①式這些特點,用怎樣的一個量來替代MP或-MP,可以使上面的表示更簡潔?
答:建直角坐標系,利用P的縱坐標替代MP或-MP.
4.建構三角函數的定義
任意的角的正弦一種定義方法.
(1)把α“放到直角坐標系內”.
(2)以原點為圓心,半徑r 作圓,
又與α的終邊相交于點P 坐標為(x,y).
(3)規定:sinα=yr.
5.分析:以上規定是否合理?
問題一:當α為銳角時,此規定與初中定義矛盾嗎?
結論:不矛盾,而且坐標法的引入擺脫了銳角的束縛.
問題二:圓的半徑r大小有限定嗎?
結論:根據相似三角形的知識,對于確定的角α,這個比值不會隨點P在α的終邊上的位置的改變而改變,是唯一確定的.
問題三:半徑r取多少時,會使得比值更加簡潔?
結論:可以考慮取r=1,這樣的圓我們稱單位圓.
即:在直角坐標系中,以原點為圓心,以單位長度1為半徑的圓.
(意圖:可以打破知識結構的平衡,感受到學習新知識的必要性——角的范圍擴大了,銳角三角函數也應該“與時俱進”,并不顯得突然.把定義的主動權交給學生,引導學生參與定義過程發展思維.)
6.導出任意角的三角函數定義
設α是一個任意角,它的終邊與單位圓交于點P(x,y),那么,
y叫做α的正弦,記作sinα,即sinα=y;
x叫做α的余弦,記作cosα,即cosα=x;
yx叫做α的正切,記作tanα,即tanα=yxx≠0.
正弦、余弦、正切都是以角為自變量,以單位圓上點的坐標或坐標的比值為函數值的函數,我們將它們統稱為三角函數.使比值有意義的角的集合即為三角函數的定義域.
7.歸納總結,注重滲透
本節課通過對實際問題的解決,學習了任意三角函數的概念.請同學們簡要回顧探究過程.三角函數的定義可謂“看似平凡最崎嶇.成如容易卻艱辛.”(王安石詩).早期的三角學隸屬于天文學,為了天文觀測的需要,與古希臘幾何有不可分割的聯系.盡管三角知識起源較早,但在歐拉以前,人們對三角函數的研究大都在一個半徑不定的圓內進行的,運用起來很不方便.直到歐拉時代,才令圓的半徑為1,置角于單位圓中,把三角函數定義為相應的線段與圓半徑1之比.教材中現在的定義與歷史上大數學家歐拉的定義是一致的.歐拉用直角坐標來定義三角函數,徹底解決了三角函數在四個象限中的符號問題,使三角函數成為研究現實世界中周期變化現象的“最有表現力的函數”.
(設計意圖:對教學內容進行歸納、疏理、提升.有意加強數學文化的熏陶,讓學生在數學學習中尋求數學發展的歷史軌跡,感受數學家們嚴謹治學和鍥而不舍的探索創新精神,從而提升自身的文化素養和創新意識.)
【參考文獻】
[1]簡洪權.高中數學運算能力的組成及培養策略[J].中學數學教學參考,2000.1-2.
[2]張衛國.例談高考應用題對能力的考查[J].中學數學研究,2001.3.

