一種新型連續可調光程發生系統安裝誤差研究

丁紅昌，陳小杰，韋湘宜，曹國華

（長春理工大學　機電工程學院，長春 130022）

?

一種新型連續可調光程發生系統安裝誤差研究

丁紅昌，陳小杰，韋湘宜，曹國華

（長春理工大學機電工程學院，長春 130022）

摘 要：針對傳統的光程發生系統所具有的光程不可調、安裝精度要求過高等問題。首先提出了一種光程連續可調的光程發生系統。該系統由3個反射鏡片組所組成，光束從一端入射，經過3個鏡片組的連續反射，從另一端出射。利用矩陣變換建立出射光線和入射光線的函數關系式，該表達式說明該系統具有連續可調、分辨率高等特點。在此基礎上并進一步推導出總光程表達式opd= G（ h， R， d， ru， rsd ）。傳統的光程發生系統所具有的安裝精度要求過高問題，即必須保證上一個鏡片的安裝精度才能進行下一個鏡片的裝調，鏡片的裝配精度具有耦合性。為此首先解算出一個最佳入射角度，然后建立以3個鏡片的平移、旋轉的安裝允許安裝誤差為目標函數的非線性有約束規劃模型，利用遺傳算法求出3個鏡片單獨的最佳容差范圍，從而實現了鏡片安裝精度的解耦。實際裝調中，只需分別保證3個鏡片的裝調精度在各自的允許安裝誤差帶內即可保證總體的安裝精度。該模型實現了鏡片裝調的解耦對于實際光學系統的安裝調試具有很好的指導意義。

關鍵詞：連續可調光程發生系統；安裝誤差；誤差分析；優化規劃；遺傳算法

0　引言

光程發生系統在航空航天、環境監測、通信等到很多場合具有重要意義，傳統的光程發生系統只能利用定長光線產生固定的光程［1］，其光程不可調節。同時鏡片安裝時耦合性過高，首先要保證上一個鏡片的安裝精度才能進行下一個鏡片的安裝。為了解決這兩個問題，本文首先提出一種光程連續可調的光程發生系統。接著為了解決安裝時過高的安裝耦合性，首先解算出最佳的入射角度，接著建立了以3個鏡片的位移、旋轉安裝允許公差為自變量，最佳容許安裝誤差為目標函數的約束規劃模型。求解此模型得到3個鏡片分別的最大安裝容許公差，即實現了鏡片安裝精度要求的解耦。應用此模型，實際安裝調試中只需分別保證單個鏡片在允許內的安裝容許公差帶內，即可保證總體的安裝精度。

1　連續可調光程發生系統模型建立

連續可調光程發生系統的主要由三個具有相同的曲率半徑的反射鏡組成。光線從一端射入，經過反射鏡組的多次反射之后從另一端射出。其示意圖如圖1所示。通過調節右邊兩個鏡片的垂直距離來改變光程。

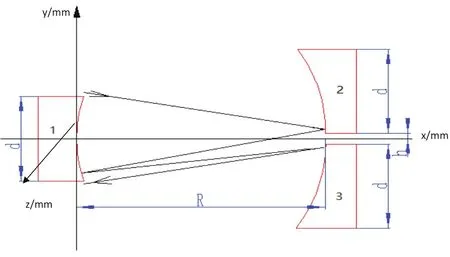
圖1　光程發生系統示意圖

1.1連續可調光程發生系統的模型建立

建立如圖1所示的坐標系，入射光線（rux0，ruy0，ruz0）經過3個鏡片組的連續反射得到出射光線（chux，chuy，chuz）。聯立鏡片方程與光線方程求解出入射光線與鏡片的交點（xi，yi，zi）。

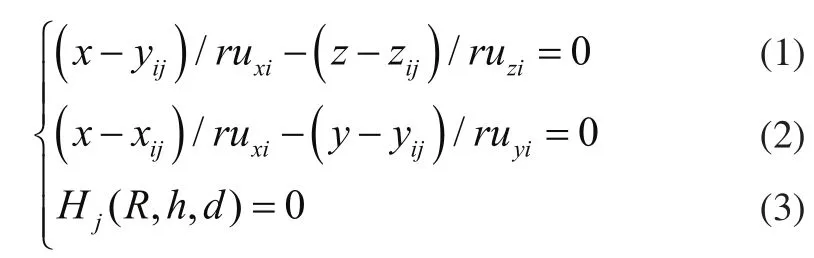
其中，i表示第i次入射，j取1、2、3分別表示1、2、3鏡片。Hj（R，h，d）表示第j個鏡片的方程。

由旋轉變換矩陣可以求得入射光線（ruxi，ruyi，ruzi）經過鏡片反射之后得到的新入射光線（ruxi+1，ruyi+1，ruzi+1）［2］。由歐式空間距離公式可得光程表達式為：

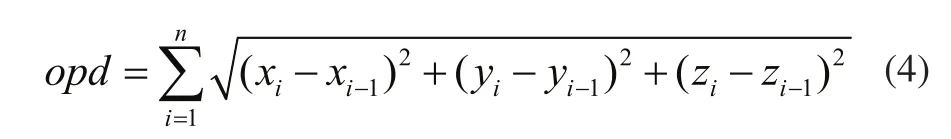
1.2連續可調光程發生系統的最佳入射方向向量

在理想情況下，鏡片安裝沒有安裝誤差。可以求得容許入射光線變化最大的最佳入射角度。在此角度下，鏡片的入射光線在容許的偏轉范圍內，出射光線都可以被接收器接收到。構造出以最佳接收效果為性能指標的約束優化模型，根據系統本身具有的物理特性列寫約束方程。求解此優化模型即可得出最佳入射角度。

以最佳接受效果為性能指標的目標函數：

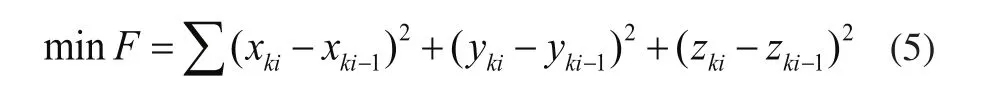
根據接收器接受范圍，鏡片尺寸參數列出約束條件：

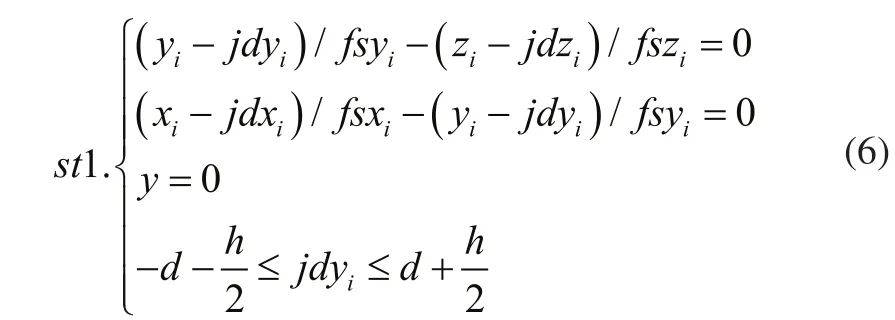
其中fs=（fsxi，fsyi，fszi）為方向向量，（jdxi，jdyi，jdzi）為第i次的入射向量與鏡片的交點。即fs滿足：

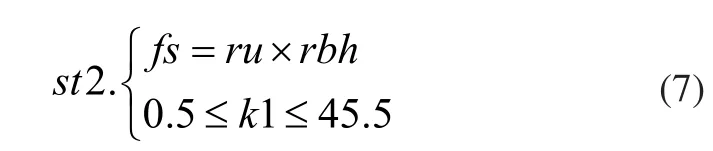
求解此非線性有約束優化模型即可求出最佳入射向量

2　鏡片組實際安裝最大容許誤差研究

實際工程中，鏡片安裝總有安裝誤差。傳統的鏡片安裝往往需要保證上個鏡片的裝配精度，才能裝配調整下一個鏡片，裝配精度要求過高。本文建立的數學模型能夠在保證總體安裝精度要求下，求解出單個鏡片能夠達到的的最大容許誤差。實際裝調中，只需滿足單個鏡片的裝配精度，即可滿足總體裝配精度。

仿照第一節最佳入射向量的求解，可以類似求解出在保證總體安裝精度的前提下，3個鏡片分別獨立允許的最大安裝允許誤差［4］。

保證總體安裝精度下，衡量3個鏡片最佳獨立安裝允許誤差目標函數：

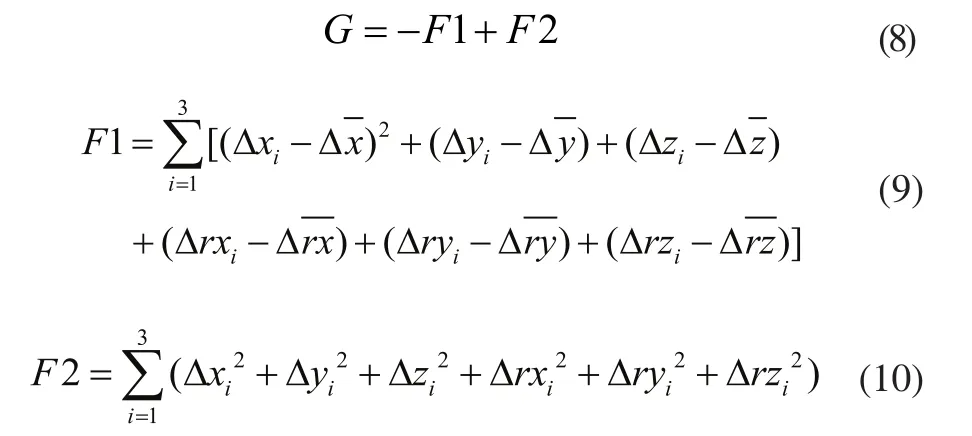
目標函數分為兩項，其中F1是用來衡量每個鏡片安裝誤差分布的分散程度，F2是用來衡量其允許的安裝誤差的大小。其中（xi，yi，zi，rxi，ryi，rzi）為鏡片i的最佳位置。定義（?xi，?yi，?zi，?rxi，?ryi，?rzi）為第i個鏡片安裝時所允許的最大誤差。

約束條件：

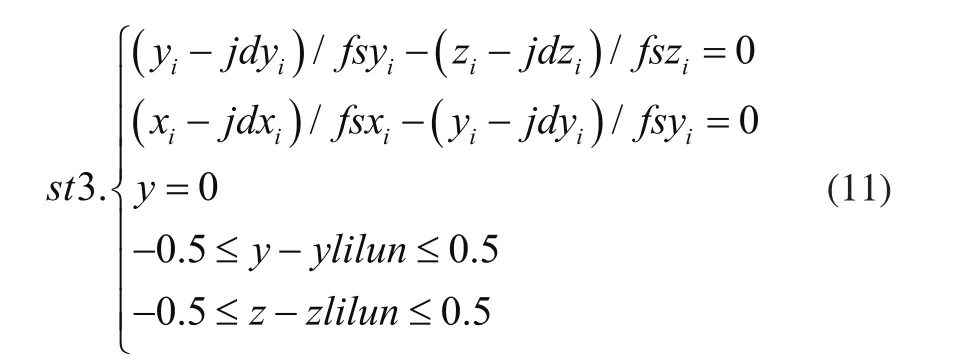
其中（xlilun，ylilun，zliun）為理想安裝下的最佳位置出射光線與接收器所在平面的交點。

求解此優化模型即可得出單個鏡片分別所允許的最大安裝誤差。應用此模型，只需保證每個鏡片在所允許的安裝誤差帶內，即可保證總體的安裝精度，即實現了鏡片安裝精度的解耦。

3　實例驗證和結果分析

以接收器半徑大小為0.5mm對該模型進行驗證，實例中的參數如表1所示。

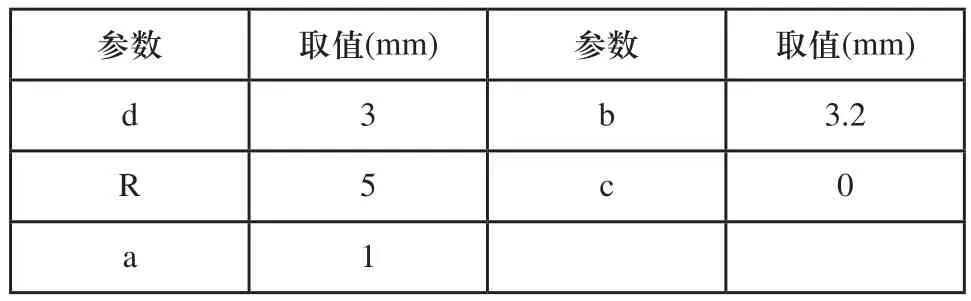
表1　實例驗證中參數

3.1光程表達式

聯立方程（1）～（11）求出光程的表達式如下形式：

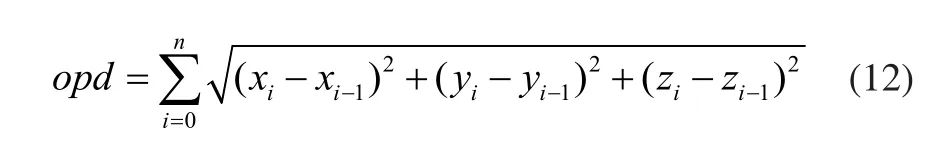
其中，（xi，yi，zi）為第i次入射光線與鏡片的交點。顯然（xi，yi，zi）與鏡片間的距離h有關。圖2是其MATLAB求解仿真示意圖。

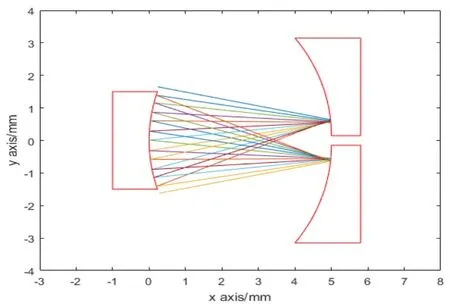
圖2　MATLAB仿真求解示意圖

3.2單個鏡片的安裝容許公差帶

將參數代入第三節的優化模型即可求解出在保證總體安裝精度下，3個鏡片分別的安裝容許公差帶。由于本問題的約束函數較復雜，傳統的優化算法在此不適用。為此采用遺傳算法求解［6］。聯立式（8）～式（10），利用MATLAB即可求解出3個鏡片各自的安裝容許公差帶。黑色矩形區域內即為每個鏡片的平移和旋轉安裝容許公差帶。

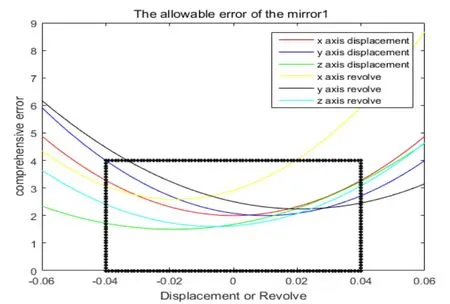
圖3　鏡片1安裝容差范圍

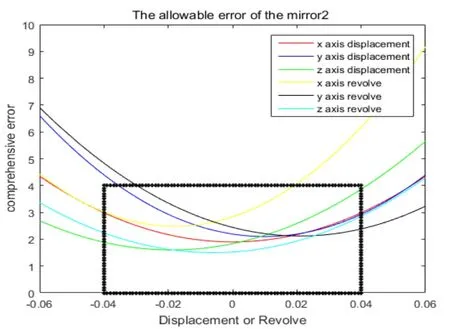
圖4　鏡片2安裝容差范圍

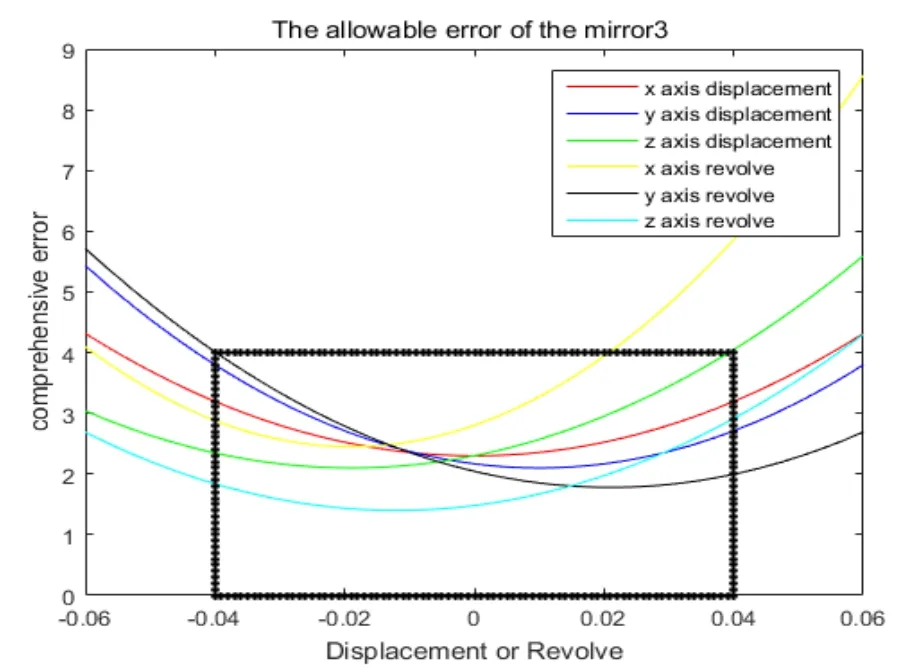
圖5　鏡片3安裝容差范圍

3.3結論分析

由圖（3）～圖（5）可以清晰地看出在保證總體安裝精度要求下每個鏡片所允許的安裝公差帶。黑色矩形區域代表著每個鏡片XYZ軸所允許的最大平移和旋轉安裝公差帶。相對于傳統的必須保證上一個鏡片裝調精度才能裝調下一個鏡片的裝配方式，本文提出的裝配方式，只需每個鏡片的安裝誤差都在各自黑色矩形容許安裝誤差區域內，即可保證總的裝配精度。顯然后者裝配簡單，這對于實際裝調具有重要指導意義。

4　結束語

為了解決傳統光程發生系統具有的光程不可調和鏡片安裝調試困難兩個問題。首先提出了一種連續可調光程發生系統，推導出光程和鏡片組距離h的表達式。通過調整h的大小，即可改變光程的大小。接著為了解決傳統的鏡片安裝調試困難，即必須保證上一個鏡片的安裝鏡片，才能安裝調試下一個鏡片。本文提出的模型只需保證每個鏡片在各自的允許公差帶內，即可保證總的安裝精度要求。最后通過仿真實驗驗證了該模型的實用性，實際應用中，只需保證每個鏡片在各自的允許安裝黑色矩形誤差帶內，即可保證總的安裝精度要求。該模型對于實際的裝配調試具有很好的指導意義。

參考文獻：

［1］ 史潔琴，何珂，徐永.光纖基線標定激光測距儀方法研究［J］.南京航空航天大學學報，2002，（44）16：830-834.

［2］ 王衛東.計算機圖形學基礎［M］.西安電子科技大學出版社，2009（9）.

［3］ 喬達諾（Giordano，F.R.）等.數學建模［M］.北京：機械工業出版社， 2003.05.

［4］ Francis S Hill Jr， Stephen M Kelley. 計算機圖形學（OpenGL版）［M］.胡事民，劉利剛，等譯.3版.清華大學出版社，2009.

［5］ （日）玄光男，（日）遺傳算法與工程優化［M］.程潤偉，于歆杰，周根貴，譯.北京：清華大學出版社，2004.01.

［6］ 黃席樾，向長城，殷禮勝，著.現代智能算法理論及應用（第2冊）［M］.北京：科學出版社，2009.

Erection tolerance analysis of a new continuous and adjustable optical path system with high resolution

DING Hong-chang， CHEN Xiao-jie， WEI Xiang-yi， CAO Guo-hua

中圖分類號：O439

文獻標識碼：A

文章編號：1009-0134（2016）05-0155-03

收稿日期：2016-02-15

基金項目：光頻梳激光位移傳感器設計開發（20140203017GX）

作者簡介：丁紅昌（1980 -），男，遼寧撫順人，講師，博士，主要從事光電在線檢測技術方面的研究。