鋼拉桿三角形和梯形螺紋螺牙受力分析★

張平　陸志杰（河北大學(xué)建筑工程學(xué)院，河北　保定　071000）

?

鋼拉桿三角形和梯形螺紋螺牙受力分析★

張平陸志杰
（河北大學(xué)建筑工程學(xué)院，河北保定071000）

摘要：分析了傳統(tǒng)鋼拉桿螺紋強(qiáng)度計(jì)算中存在的問(wèn)題，以某鋼拉桿梯形螺紋和三角形螺紋為例，建立了有限元模型，并對(duì)螺紋根部受力進(jìn)行了研究，探討了其失效機(jī)理，結(jié)果表明用ANSYS建立的螺紋牙模型變形較小，應(yīng)力分析更加精確，符合實(shí)際受力情況。關(guān)鍵詞：鋼拉桿，螺紋牙，有限元模型，等效應(yīng)力

★：河北大學(xué)研究生創(chuàng)新項(xiàng)目“鋼拉桿三角螺紋和梯形螺紋強(qiáng)度計(jì)算研究”（項(xiàng)目編號(hào)：X2015087）

1　存在的問(wèn)題

目前，螺紋連接可以采用普通螺紋、梯形、矩形、鋸齒形等四種形式，其中普通螺紋使用較為普遍，在工業(yè)生產(chǎn)中計(jì)算鋼拉桿螺紋牙型強(qiáng)度時(shí)通常采用國(guó)內(nèi)傳統(tǒng)螺紋強(qiáng)度計(jì)算方法（機(jī)械設(shè)計(jì)手冊(cè)）。校核方法為：把螺紋牙展成一根懸臂梁的形式，見(jiàn)圖1，其中設(shè)軸向應(yīng)力為F，相旋合螺紋圈數(shù)為z。

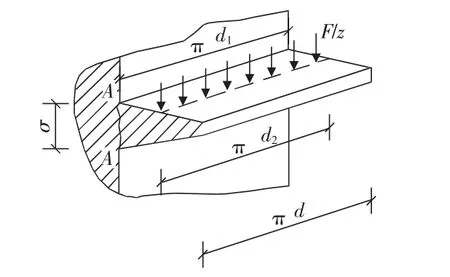
圖1　螺紋牙受力圖

其中，［τ］為許用切應(yīng)力，MPa；［σ］b為許用彎曲應(yīng)力，MPa。

錢(qián)學(xué)毅［3］通過(guò)對(duì)螺紋牙（Tr48×12—8，Tr44×12—8和B40× 7等）的有限元受力分析對(duì)理論計(jì)算方法提出3個(gè)問(wèn)題：1）從模型上看，將螺旋形狀的螺紋牙力學(xué)模型簡(jiǎn)化成長(zhǎng)度遠(yuǎn)大于橫截面尺寸的懸臂梁模型與實(shí)際情況差別較大，由此而導(dǎo)出的彎曲強(qiáng)度條件與實(shí)際情況差別較大；2）展開(kāi)成懸臂梁的力學(xué)模型應(yīng)力的分布規(guī)律較之實(shí)際的螺旋形模型也不相同；3）沒(méi)有考慮剪切對(duì)彎曲正應(yīng)力的影響。事實(shí)上，螺紋牙根是處于非桿件復(fù)雜應(yīng)力狀態(tài)，不應(yīng)該再用材料力學(xué)的理論進(jìn)行分析計(jì)算。而應(yīng)該運(yùn)用彈性理論進(jìn)行分析計(jì)算，取等效正應(yīng)力作為彎曲強(qiáng)度計(jì)算的依據(jù)，而不應(yīng)該僅考慮由彎矩引起的正應(yīng)力。錢(qián)學(xué)毅等人的研究是相對(duì)于較小的螺紋螺牙進(jìn)行的，然而在實(shí)際中還經(jīng)常用到較大螺紋牙的鋼拉桿進(jìn)行工業(yè)生產(chǎn)。

粗牙（較大螺紋牙）和細(xì)牙（小螺紋牙）的區(qū)別：螺距大小不同，粗牙螺距大，細(xì)牙小；粗牙螺紋抗疲勞能力強(qiáng)一些，對(duì)經(jīng)常拆裝方便一些；細(xì)牙自鎖能力強(qiáng)，底徑尺寸大，靜載能力強(qiáng)。另外細(xì)牙的擰緊力矩是小一些，鋼級(jí)與預(yù)緊能力有一定關(guān)系，在同樣預(yù)緊力時(shí)細(xì)牙是小一些。本文中將對(duì)較大螺紋牙的鋼拉桿受力進(jìn)行分析。

2　建立有限元模型

1）以某一鋼拉桿梯形螺紋Tr140×10和三角形螺紋M85×6為實(shí)例。鋼拉桿共有4種屈服強(qiáng)度（345，460，550，650），屈服載荷為桿體直徑的截面積與屈服強(qiáng)度值相乘。不同屈服強(qiáng)度的鋼拉桿的螺紋要承受相對(duì)應(yīng)的載荷值。梯形螺紋Tr140×10，公稱(chēng)直徑d =140 mm，螺距P = 10 mm，基本牙型高H = 5.5 mm，中徑d2=135 mm，小徑d3=129 mm，牙型角α=30°，螺紋材料為345級(jí)φ120鋼拉桿，理論屈服載荷為3 900 kN，彈性模量E =210 GPa，泊松比μ=0.27，每圈螺紋受力F =3.9 kN。三角形螺紋M85×6，公稱(chēng)直徑d =85 mm，螺距P =6 mm，基本牙型高H =5.2 mm，中徑d2= 81.1 mm，小徑d3=78.5 mm，牙型角α= 60°，螺紋材料為345級(jí)φ70鋼拉桿，理論屈服載荷為1 327 kN，彈性模量E =210 GPa，泊松比μ=0.27，每圈螺紋承受的作用力F =13.27 kN。

2）有限元模型的建立［4，5］。ANSYS單元庫(kù)中提供了超過(guò)150種的不同單元類(lèi)型，根據(jù)鋼拉桿螺紋螺牙的特點(diǎn)選用Solid187單元進(jìn)行離散網(wǎng)格劃分，Solid187單元是一個(gè)高階3維10節(jié)點(diǎn)固體結(jié)構(gòu)單元，具有二次位移模式可以更好地模擬不規(guī)則的模型，計(jì)算精度高，利用ANSYS14.0建立精確幾何模型及有限元模型見(jiàn)圖2，圖3，圖形2共8 433單元，14 312節(jié)點(diǎn)，圖形3共12 674單元，20 734節(jié)點(diǎn)。

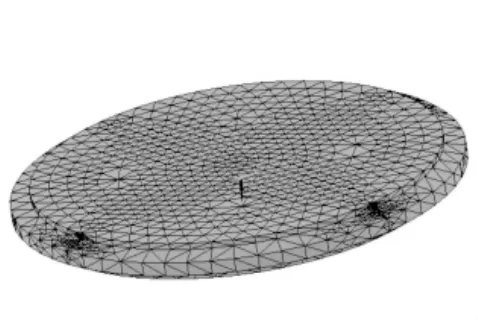
圖2　梯形螺紋模型　

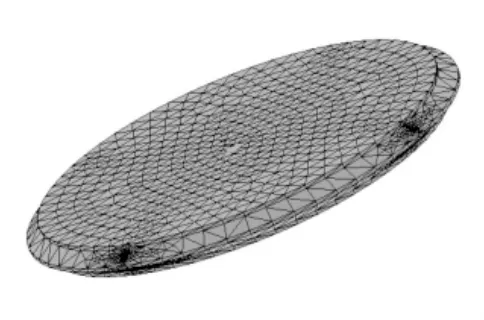
圖3　三角形螺紋模型

3　有限元分析

1）根據(jù)鋼拉桿螺紋牙的實(shí)際工況，將螺桿小徑的橫截面固定即施加Ux，Uy，Uz三向完全約束。2）在梯形螺桿面上施加大小為3 900 N均勻分布的面載荷，在三角形螺桿面上施加大小為13 270 N均勻分布的面荷載。3）對(duì)特定工況下的以上2種有限元模型進(jìn)行計(jì)算求解應(yīng)力分析。

4　結(jié)果分析

經(jīng)過(guò)ANSYS有限元計(jì)算，導(dǎo)出精確有限元模型等效應(yīng)力云圖見(jiàn)圖4，圖5，梯形螺紋等效應(yīng)力的最大值為7 039.8 N，三角形螺紋等效應(yīng)力的最大值為22 496 N。螺紋牙頂部變形較大，但在允許形變范圍以?xún)?nèi)。

圖4　梯形螺紋等效應(yīng)力云圖

圖5　三角形螺紋等效應(yīng)力云圖

與傳統(tǒng)的用懸臂梁的計(jì)算方法相比較，相同受力條件下，用ANSYS建立的圓形螺紋牙模型變形較小，應(yīng)力分析更加精確，該方法使模型建立更加方便，符合實(shí)際受力情況，計(jì)算結(jié)果變形在允許的范圍內(nèi)，能達(dá)到滿意的變形精度。

參考文獻(xiàn)：

［1］徐灝.機(jī)械設(shè)計(jì)手冊(cè)［M］.第2版.北京：機(jī)械工業(yè)出版社，2003.

［2］吳宗澤.機(jī)械設(shè)計(jì)［M］.北京：高等教育出版社，2001.

［3］錢(qián)學(xué)毅.鋸齒形螺紋壓根應(yīng)力有限元仿真分析［M］.北京：起重運(yùn)輸機(jī)械出版社，2008.

［4］張朝暉.ANSYS11.0結(jié)構(gòu)分析工程應(yīng)用實(shí)例解析［M］.北京：機(jī)械工業(yè)出版社，2008.

［5］ANSYS APDL參數(shù)化有限元分析技術(shù)及其應(yīng)用實(shí)例［M］.北京：中國(guó)水利水電出版社，2013.

［6］邱榮茂，王大鳴.螺紋的三維建模［J］.現(xiàn)代制造工程，2003 （7）：92-93.

［7］錢(qián)學(xué)毅，吳雙，鄒麗梅，等.基于FEM的滑動(dòng)螺旋副螺紋牙根應(yīng)力計(jì)算及PDS仿真分析［J］.輕工機(jī)械，2008（1）：62-63.

中圖分類(lèi)號(hào)：TU602

文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1009-6825（2016）06-0223-02

收稿日期：2015-12-18

作者簡(jiǎn)介：張平（1990-），男，在讀碩士；陸志杰（1990-），男，在讀碩士

The force analysis on steel rod triangle and trapezoid thread★

Zhang Ping Lu Zhijie
（Construction Engineering School，Hebei University，Baoding 071000，China）

Abstract：This paper analyzed the existing problems in traditional steel rod thread strength calculation，taking a steel rod trapezoidal thread and triangle thread as an example，established the finite element model，and researched the whorl root stress，discussed its failure mechanism，the results showed that using ANSYS to establish a thread model had small deformation，the stress analysis more accurate and accord with force situation.

Key words：steel rod，thread，finite element model，equivalent stress