基于分布式圖計(jì)算框架的好友推薦算法研究
趙馬沙 周 薇 張 豪 韓冀中
1(中國(guó)科學(xué)院信息工程研究所信息智能處理技術(shù)研究室 北京 100093)2(中國(guó)科學(xué)院大學(xué) 北京 100049)3(重慶郵電大學(xué)通信與信息工程學(xué)院 重慶 400065)
?
基于分布式圖計(jì)算框架的好友推薦算法研究
趙馬沙1,2周薇1,2張豪3韓冀中1
1(中國(guó)科學(xué)院信息工程研究所信息智能處理技術(shù)研究室北京 100093)2(中國(guó)科學(xué)院大學(xué)北京 100049)3(重慶郵電大學(xué)通信與信息工程學(xué)院重慶 400065)
摘要隨著社交網(wǎng)絡(luò)的興起與發(fā)展,用戶數(shù)目規(guī)模呈現(xiàn)出指數(shù)級(jí)增長(zhǎng)的趨勢(shì)。這些大規(guī)模數(shù)據(jù)里蘊(yùn)含著許多有價(jià)值的信息,挖掘其中有用的信息已經(jīng)成為學(xué)者研究的重點(diǎn),好友推薦就是數(shù)據(jù)挖掘里的一個(gè)重要應(yīng)用。為了獲得更優(yōu)的性能、更高的可擴(kuò)展性,采用分布式平臺(tái)解決大規(guī)模好友推薦成為學(xué)術(shù)界和工業(yè)界的一個(gè)發(fā)展趨勢(shì)。目前使用得較廣泛的為基于MapReduce框架的好友推薦算法,該方法有較高的可擴(kuò)展性,但是受限于MapReduce低效的中間數(shù)據(jù)傳輸,存在性能缺陷。針對(duì)上述問(wèn)題,提出一種基于分布式圖計(jì)算框架的好友推薦算法。最后,在多個(gè)真實(shí)的社交網(wǎng)絡(luò)數(shù)據(jù)集上評(píng)測(cè)了該方法。實(shí)驗(yàn)結(jié)果表明,該方法要優(yōu)于業(yè)界先進(jìn)的好友推薦算法,在準(zhǔn)確率相當(dāng)?shù)那闆r下,性能大約為其他算法的7倍。
關(guān)鍵詞好友推薦分布式圖計(jì)算框架隨機(jī)游走
0引言
隨著Web2.0的出現(xiàn)及興起,社交網(wǎng)絡(luò)得到了蓬勃發(fā)展,用戶數(shù)越來(lái)越多。2014年一月份的調(diào)查表明[1],Twitter[2]每月的平均活躍用戶人數(shù)高達(dá)2.41億。2014年5月,QQ空間官方聲稱其每月的平均活躍用戶高1.2億。這些大規(guī)模數(shù)據(jù)里蘊(yùn)藏著許多潛在的有價(jià)值信息,而挖掘其中的有用信息已經(jīng)成為業(yè)界學(xué)者的一個(gè)研究重點(diǎn)。其中好友推薦[3]就是數(shù)據(jù)挖掘[4]的一個(gè)非常重要的應(yīng)用,目前已經(jīng)被廣泛地應(yīng)用在各類社交網(wǎng)站上。
目前的好友推薦算法主要分為兩種[5],一種是基于局部信息的,比如已經(jīng)被廣泛應(yīng)用于社交網(wǎng)絡(luò)的二度人脈(好友的好友)好友推薦。這種基于局部信息的算法計(jì)算復(fù)雜度低,運(yùn)行消耗的時(shí)間少,但因其利用的信息量少,所以準(zhǔn)確率不高。第二種是基于全局信息的好友推薦算法,算法通常會(huì)偵測(cè)整個(gè)社會(huì)圖的所有路徑結(jié)構(gòu),由于其利用了更多的信息,所以推薦結(jié)果更加準(zhǔn)確。但是對(duì)于大規(guī)模的在線社交網(wǎng)絡(luò)來(lái)說(shuō),這類方法的計(jì)算成本相當(dāng)高,不適用實(shí)時(shí)推薦。
針對(duì)以上缺陷,有學(xué)者提出了基于局部隨機(jī)游走的好友推薦算法[6]。它根據(jù)“小世界”理論[7],隨機(jī)游走有限范圍內(nèi)的所有路徑,為用戶提供了既快速又準(zhǔn)確的朋友推薦。
為了應(yīng)對(duì)日益增長(zhǎng)的社交網(wǎng)絡(luò)數(shù)據(jù),分布式好友推薦算法也得到了研究學(xué)者的青睞。目前使用得較為廣泛的是基于MapReduce的大規(guī)模好友推薦算法[8]。該算法擁有較高的可擴(kuò)展性,能應(yīng)對(duì)日益增長(zhǎng)的社交網(wǎng)絡(luò)數(shù)據(jù)。但由于MapReduce框架中間數(shù)據(jù)的持久化機(jī)制,在其上實(shí)現(xiàn)的好友推薦算法性能較低。
針對(duì)以上問(wèn)題,本文提出一種基于分布式圖計(jì)算框架的好友推薦方法。該方法結(jié)合了局部隨機(jī)游走和分布式圖計(jì)算框架,實(shí)現(xiàn)了好友推薦迭代計(jì)算,中間數(shù)據(jù)采用消息傳遞的模式,減少了數(shù)據(jù)持久化的代價(jià)。最后,在分布式集群下評(píng)測(cè)了本文提出的方法,使用多個(gè)真實(shí)的大規(guī)模社交網(wǎng)絡(luò)公開(kāi)數(shù)據(jù)集。實(shí)驗(yàn)結(jié)果表明,該方法在性能上比單機(jī)的好友推薦算法提高了4倍,比基于MapReduce框架的算法提升了7倍,并且該算法具有較高的可擴(kuò)展性,隨著集群規(guī)模的增長(zhǎng)成正比增長(zhǎng)。
1相關(guān)工作
好友推薦算法有很多,社會(huì)學(xué)中的同質(zhì)性理論認(rèn)為,擁有相同愛(ài)好的人更可能成為朋友,所以很多社交平臺(tái)通過(guò)用戶屬性的相似度來(lái)推薦好友[9,10]。比如百度利用用戶的愛(ài)好等屬性推薦朋友。
還有一種方法就是利用好友關(guān)系的網(wǎng)絡(luò)拓?fù)鋱D[11],主要有兩類:一類是基于社會(huì)網(wǎng)絡(luò)結(jié)構(gòu)的局部特性,比如二度人脈FOAF(FriendofaFriend)的方法[12]。它基于這樣的現(xiàn)象:如果兩個(gè)人有很多共同的朋友,那么他們?cè)趯?lái)就很有可能成為朋友。由于FOAF的簡(jiǎn)單高效,所以Facebook、騰訊QQ等均采用它為用戶推薦潛在好友。但是,這種基于網(wǎng)絡(luò)局部特性的方法由于利用的信息不充分,得到的結(jié)果往往不是很準(zhǔn)確。另一類方法是基于社會(huì)網(wǎng)絡(luò)的全局特性,探索社會(huì)網(wǎng)絡(luò)圖中的所有路徑結(jié)構(gòu),比如經(jīng)典的Google網(wǎng)頁(yè)排序算法PageRank[13],利用了整個(gè)圖結(jié)構(gòu)的信息。雖然這種算法提高了結(jié)果的準(zhǔn)確性,但是在現(xiàn)實(shí)的社交網(wǎng)絡(luò)中,用戶數(shù)目通常是上百萬(wàn)、千萬(wàn)甚至是億,運(yùn)行這種算法成本太大,消耗的時(shí)間太多,也不適合應(yīng)用在實(shí)時(shí)推薦上。
為了解決上述問(wèn)題,有學(xué)者提出了一個(gè)基于局部隨機(jī)游走的好友推薦算法。這個(gè)方法考慮了更多的鄰居信息,具有更高的準(zhǔn)確性;同時(shí)比起基于全局的方法,由于無(wú)需遍歷整個(gè)社會(huì)圖,因此其具有更低的時(shí)間復(fù)雜度。
上述所有的方法都是為單機(jī)而設(shè)計(jì)的,當(dāng)社交網(wǎng)絡(luò)用戶數(shù)增多,面對(duì)復(fù)雜的大規(guī)模好友推薦時(shí),就會(huì)出現(xiàn)計(jì)算效率的問(wèn)題,而且不具有很好的可擴(kuò)展能力。于是一些學(xué)者開(kāi)始研究可擴(kuò)展的分布式好友推薦算法,通過(guò)集群的計(jì)算能力來(lái)應(yīng)對(duì)大規(guī)模數(shù)據(jù)帶來(lái)的挑戰(zhàn)。文獻(xiàn)[14]提出了基于MapReduce框架的分布式好友推薦方法,該方法采用MapReduce的Key-Value結(jié)構(gòu)實(shí)現(xiàn)了二度人脈等好友推薦算法[15]。盡管MapReduce具有較高的可擴(kuò)展性,但是其低效的中間數(shù)據(jù)共享方式導(dǎo)致了該方法的性能不高。
2相關(guān)背景
2.1BSP模型
大同步并行BSP(BulkSynchronizationParallel)模型是由哈佛大學(xué)Valiant和牛津大學(xué)BillMcColl提出的并行計(jì)算模型。BSP模型是一種包含一個(gè)主節(jié)點(diǎn)和多個(gè)從節(jié)點(diǎn)的分布式的模型。每個(gè)從節(jié)點(diǎn)負(fù)責(zé)處理圖中的一個(gè)子圖,作業(yè)的處理是由迭代的過(guò)程組成,每次迭代稱為一個(gè)超步。超步是在數(shù)據(jù)處理中的最小計(jì)算單位,主要包括三個(gè)階段:并行計(jì)算、通信和柵欄同步,如圖1所示。
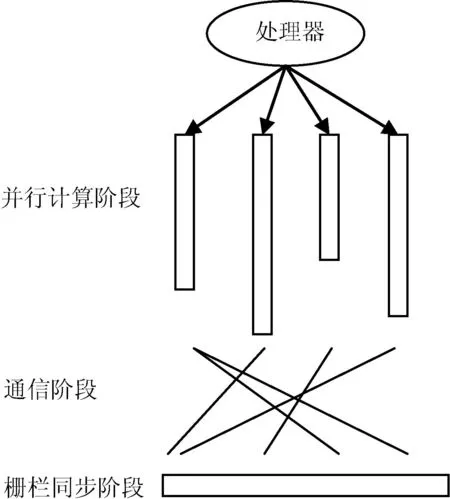
圖1 BSP超步的三個(gè)階段
1) 本地計(jì)算階段,每個(gè)節(jié)點(diǎn)只處理本節(jié)點(diǎn)維護(hù)的數(shù)據(jù)。
2) 全局通信階段,每個(gè)節(jié)點(diǎn)將本地計(jì)算的結(jié)果發(fā)送給鄰居節(jié)點(diǎn)。
3) 柵欄同步階段,等待所有通信行為結(jié)束。
在一個(gè)確定的超步中,一個(gè)從節(jié)點(diǎn)只有在上一個(gè)超步中接收到所有來(lái)自相鄰頂點(diǎn)的消息才可以處理這一個(gè)頂點(diǎn)。此外,該系統(tǒng)只有所有圖頂點(diǎn)都處理完畢之后才進(jìn)行下一個(gè)超步。
目前,很多公司已經(jīng)開(kāi)發(fā)了許多基于BSP模型的圖數(shù)據(jù)處理系統(tǒng),最著名的就是Google發(fā)明的Pregel[16]。Pregel是一種面向圖算法的分布式編程框架,采用迭代的計(jì)算模型。在每一輪,每個(gè)頂點(diǎn)處理上一輪收到的消息,并給相鄰頂點(diǎn)發(fā)消息,更新自身狀態(tài)和拓?fù)浣Y(jié)構(gòu)(出、入邊)等。類似的還有Apache的Hama[17],它是Hadoop[18]生態(tài)系統(tǒng)中的一個(gè)子項(xiàng)目,兼容很多Hadoop的分布式存儲(chǔ)系統(tǒng),如HDFS、HBase等。
由于Pregel并非開(kāi)源,我們基于Pregel的思想實(shí)現(xiàn)了BSP圖計(jì)算框架[19],本文的實(shí)驗(yàn)也是運(yùn)行在該框架上。與Pregel類似,BSP圖計(jì)算框架首先將圖分割為頂點(diǎn)不相交的子圖并將各個(gè)子圖分配到計(jì)算節(jié)點(diǎn)上,BSP圖計(jì)算框架的計(jì)算過(guò)程基于BSP模型實(shí)現(xiàn)。計(jì)算被分為多個(gè)超步,每一超步中各個(gè)計(jì)算節(jié)點(diǎn)依次調(diào)用各個(gè)頂點(diǎn)的更新函數(shù)。在頂點(diǎn)更新函數(shù)中,每個(gè)頂點(diǎn)可以根據(jù)所收到的上一輪的消息更新該頂點(diǎn)的狀態(tài)并產(chǎn)生本輪發(fā)送給其他頂點(diǎn)的消息。待所有圖頂點(diǎn)均更新完畢且所有消息均已到達(dá)目標(biāo)節(jié)點(diǎn),各計(jì)算節(jié)點(diǎn)進(jìn)行柵欄同步并同時(shí)進(jìn)入下一超步。這一過(guò)程循環(huán)往復(fù)直至所運(yùn)行的算法達(dá)到收斂條件。因此,基于BSP框架實(shí)現(xiàn)圖算法時(shí),主要工作是通過(guò)編寫(xiě)頂點(diǎn)狀態(tài)更新函數(shù)來(lái)完成的。
2.2基于局部隨機(jī)游走的好友推薦算法
基于局部隨機(jī)游走的頂點(diǎn)間相似性是一個(gè)在社會(huì)圖的基礎(chǔ)上定義的相似性指標(biāo)。
首先給出社會(huì)圖的定義,社會(huì)圖是一個(gè)由頂點(diǎn)集合和邊集合構(gòu)成的社會(huì)網(wǎng)絡(luò),頂點(diǎn)代表用戶,邊代表用戶之間的關(guān)系,兩者之間構(gòu)成一個(gè)圖。
正式地,根據(jù)圖理論定義社會(huì)圖G=(V,E),其中V表示頂點(diǎn)集合,也就是用戶集合,E表示無(wú)向邊集合,也就是用戶之間的關(guān)系。僅當(dāng)兩個(gè)頂點(diǎn)vi、vj間的無(wú)向邊(vi,vj)∈E時(shí),vj(vi)被稱為vi(vj)的鄰接。這樣社會(huì)圖能夠表示為鄰接矩陣A=(aij)∈E,如果vi和vj為朋友,則aij=1,否則為0。

(1)
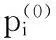
20世紀(jì)60年代,美國(guó)著名社會(huì)心理學(xué)家Milgram提出了“小世界”理論。理論指出:你和任何一個(gè)陌生人之間所間隔的人不會(huì)超過(guò)五個(gè),也就是說(shuō),最多通過(guò)五個(gè)中間人你就能夠認(rèn)識(shí)任何一個(gè)陌生人。這個(gè)理論已經(jīng)被應(yīng)用到了很多的領(lǐng)域,局部隨機(jī)游走算法的思想就是根據(jù)“小世界”假說(shuō),在社會(huì)圖上進(jìn)行有限長(zhǎng)度的隨機(jī)游走,而不是針對(duì)整個(gè)社會(huì)圖進(jìn)行全局地遍歷[20]。
(2)
其中L代表圖頂點(diǎn)vi、vj之間隨機(jī)游走的路徑長(zhǎng)度,根據(jù)“小世界”理論,可取2到6之間的整數(shù),E為社會(huì)圖中邊的總數(shù)目,Γ(j)是頂點(diǎn)vj的度,代表頂點(diǎn)的流行度,流行度指數(shù)β是一個(gè)可變參數(shù),調(diào)節(jié)頂點(diǎn)vj的流行度對(duì)相似度的影響,實(shí)驗(yàn)證明β取0.5時(shí)得出的結(jié)果最理想。
學(xué)者還通過(guò)大量的實(shí)驗(yàn)證明,在準(zhǔn)確性上,基于局部隨機(jī)游走的好友推薦算法高于基于二度好友的方法,甚至高于基于全局的推薦算法。基于全局的推薦算法雖然對(duì)社會(huì)網(wǎng)絡(luò)進(jìn)行全局遍歷,但其沒(méi)有充分地捕獲圖中頂點(diǎn)(用戶)的局部信息[21]。而基于局部隨機(jī)游走的好友推薦算法根據(jù)“小世界”假設(shè),更加注重頂點(diǎn)(用戶)附近鄰居的作用,充分利用了用戶局部信息,所以它的準(zhǔn)確性能夠高于基于全局的好友推薦方法。在性能上,基于局部隨機(jī)游走的好友推薦算法遠(yuǎn)高于基于全局的推薦算法。
3基于圖計(jì)算框架的好友推薦算法
本節(jié)描述了本文提出的一種基于分布式圖計(jì)算框架的好友推薦方法。首先介紹該方法并行化的原理,然后以算法的形式詳細(xì)介紹了圖計(jì)算迭代完成好友推薦的3個(gè)階段:初始化階段、迭代階段以及結(jié)束階段。
3.1原理
首先分析式(1),轉(zhuǎn)移概率矩陣Q就是圖中頂點(diǎn)之間互相轉(zhuǎn)移的概率。如圖2所示,aij代表頂點(diǎn)i到頂點(diǎn)j的轉(zhuǎn)移概率,也就是下一步從頂點(diǎn)i到頂點(diǎn)j的概率。矩陣中每一行代表某一個(gè)頂點(diǎn)到其他頂點(diǎn)的轉(zhuǎn)移概率,根據(jù)矩陣元素的計(jì)算公式,可以得到結(jié)論。如果頂點(diǎn)i和頂點(diǎn)j無(wú)邊,轉(zhuǎn)移概率則為0,如果有邊,轉(zhuǎn)移概率就是頂點(diǎn)i包含的邊的倒數(shù)。
圖2概率轉(zhuǎn)移矩陣Q
式(1)中出現(xiàn)了Q的轉(zhuǎn)置,轉(zhuǎn)置矩陣如圖3所示。
圖3概率轉(zhuǎn)移矩陣Q的轉(zhuǎn)置
從圖3可以看出,轉(zhuǎn)置后的矩陣中,每一行代表其他頂點(diǎn)到該頂點(diǎn)的轉(zhuǎn)移概率。
[pi0pi1pi2…pin]
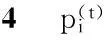
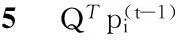
圖5是一個(gè)列向量,每一個(gè)元素是由n個(gè)加數(shù)相加得到。對(duì)每個(gè)加數(shù)ajk×pij,分析其意義,pij為頂點(diǎn)i經(jīng)過(guò)t-1步到達(dá)頂點(diǎn)j的概率,ajk為頂點(diǎn)j到達(dá)頂點(diǎn)k的概率,兩者相乘即為頂點(diǎn)i經(jīng)過(guò)t步到達(dá)頂點(diǎn)k的一部分概率,而所有的加數(shù)相加就代表頂點(diǎn)i經(jīng)過(guò)t步到達(dá)頂點(diǎn)k的概率。通過(guò)這種形式化的分析,我們就可以理解式(1)了。

3.2算法
在BSP上實(shí)現(xiàn)分布式的局部隨機(jī)游走算法分為3個(gè)階段,分別為初始化階段、迭代階段和結(jié)束階段:
1) 初始化階段:根據(jù)輸入的圖數(shù)據(jù)文件,遍歷文件中的每一行,在BSP中生成頂點(diǎn)對(duì)象,然后記錄每個(gè)頂點(diǎn)的邊。
算法1初始化圖數(shù)據(jù)
輸入:圖數(shù)據(jù)文件file
1:foreachlineinfiledo
2:vertex←createVertex(line)
//line是文件file的每一行數(shù)據(jù),vertex是BSP框架中的頂點(diǎn)對(duì)象
3:edges←getEdges(vertex)
//edges是存儲(chǔ)頂點(diǎn)所有的邊
4:endforeach
5:return
2) 迭代階段:BSP框架控制每個(gè)頂點(diǎn)運(yùn)行該階段,首先頂點(diǎn)會(huì)接受每一條邊發(fā)過(guò)來(lái)的消息,得到其中的值。然后計(jì)算p值,如果迭代次數(shù)沒(méi)有達(dá)到指定次數(shù),則繼續(xù)發(fā)消息,再次迭代,如果達(dá)到指定次數(shù),則停止。
算法2迭代階段
輸入:頂點(diǎn)vertex,頂點(diǎn)的邊edges,迭代的次數(shù)turn
1:foreachedgeinedgesdo
2:dstVertex←getDstVertex(edge)
//dstVertex是目標(biāo)頂點(diǎn)
3:value←getMessage(dstVertex)
//value是邊的權(quán)值
4:values.add(value)
5:endforeach
6:p←calculate(vertex,value)
7:ps.add(p)
8:ifturn<=STEPthen
//如果迭代次數(shù)小于STEP,繼續(xù)發(fā)消息
9:foreachedgeinedgesdo
10:dstVertex←getDstVertex(edge)
11:sendMessage(dstVertex,p)
//把p值發(fā)給每條邊
12:values.add(value)
13:endforeach
14:elsehalt()
3) 結(jié)束階段:每個(gè)頂點(diǎn)計(jì)算得到p值后,BSP框架計(jì)算出每個(gè)頂點(diǎn)和目標(biāo)頂點(diǎn)的相似度sin,然后把所有的sin存儲(chǔ)sins集合中,最后集合匯總對(duì)所有的sin進(jìn)行排序,最后按照相似度從大到小輸出。
算法3結(jié)束階段
輸入:各頂點(diǎn)的ps
輸出:各頂點(diǎn)的相似度,從大到小輸出
1:foreachvertexdo
2:sin←getSin(ps)
//sin就是相似度的值
3:sins.add(sin)
//sins存儲(chǔ)所有頂點(diǎn)的相似度
4:endforeach
5:printsort(sins)
//輸出排序的結(jié)果
6:return
4實(shí)驗(yàn)結(jié)果
4.1測(cè)試數(shù)據(jù)集和實(shí)驗(yàn)環(huán)境
為了評(píng)測(cè)本文方法的有效性,本文選取兩個(gè)好友推薦對(duì)比系:?jiǎn)螜C(jī)的局部隨機(jī)游走算法和基于MapReduce的二度人脈好友推薦算法。并在多個(gè)真實(shí)公開(kāi)的數(shù)據(jù)集上做了評(píng)測(cè)實(shí)驗(yàn),和單機(jī)的局部隨機(jī)游走算法比較。一方面證明本文提出的分布式算法是正確的,另一方面說(shuō)明分布式的算法能帶來(lái)很大的性能提升,從而可以應(yīng)付日益增長(zhǎng)的大數(shù)據(jù)集帶來(lái)的挑戰(zhàn)。和如今被很多公司廣泛用到的二度人脈算法比較,說(shuō)明本文提出的算法比現(xiàn)在流行的算法擁有更高的性能,可以在實(shí)際中應(yīng)用。實(shí)驗(yàn)環(huán)境是由4臺(tái)主機(jī)組成的集群,具體硬件配置參數(shù)如表1所示。
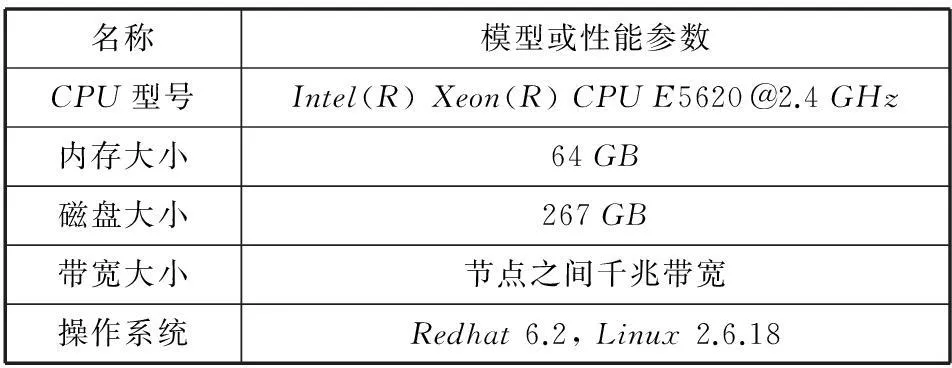
表1 實(shí)驗(yàn)環(huán)境
在數(shù)據(jù)集的選取上,本著真實(shí)公開(kāi)和全面的原則,選擇了5個(gè)不同大小的數(shù)據(jù),如表2所示。所有的數(shù)據(jù)來(lái)源各社交網(wǎng)站里,從law.di.unimi.it/datasets.php下載,由WebGraph和LLPprojects提供。這5個(gè)數(shù)據(jù)集的規(guī)模是從小到大增長(zhǎng)的,很好地說(shuō)明了本文提出的方法擁有很好的擴(kuò)展性。其次從數(shù)據(jù)集中頂點(diǎn)的平均邊數(shù)也可以看出每個(gè)圖的稀疏程度不同,說(shuō)明本文提出的方法適用面廣泛。
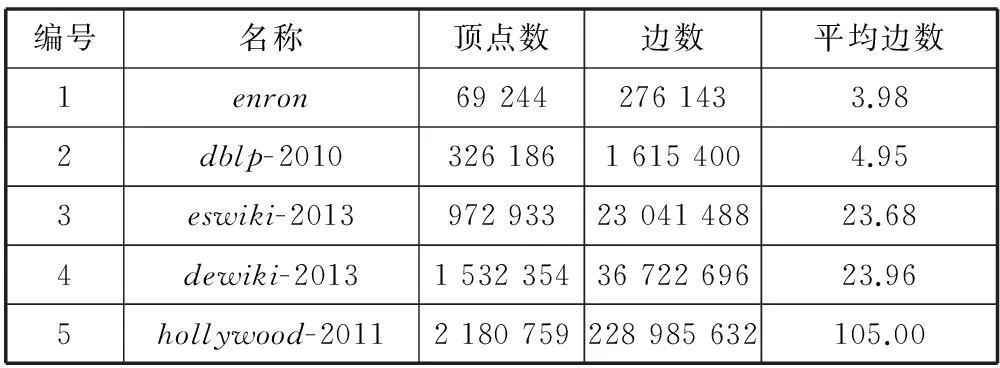
表2 實(shí)驗(yàn)數(shù)據(jù)集
4.2和單機(jī)的局部隨機(jī)游走算法比較
首先我們對(duì)分布式算法和單機(jī)算法的結(jié)果進(jìn)行了比較,實(shí)驗(yàn)表明兩種算法中相同頂點(diǎn)的相似度都是一樣的,所以局部隨機(jī)游走算法的分布式版本是正確的。
接下來(lái),我們測(cè)試了單機(jī)算法和分布式算法運(yùn)行的時(shí)間,數(shù)據(jù)如表3所示。
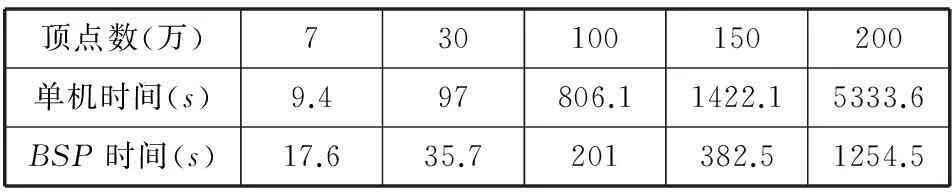
表3 分布式和單機(jī)時(shí)間對(duì)比
由表3得出的時(shí)間對(duì)比圖如圖6所示,橫坐標(biāo)是測(cè)試數(shù)據(jù)集中頂點(diǎn)的個(gè)數(shù)(大致),萬(wàn)為單位,縱坐標(biāo)是算法運(yùn)行的時(shí)間,秒為單位。
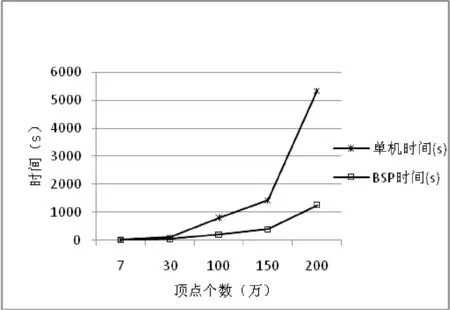
圖6 單機(jī)和并行算法時(shí)間對(duì)比圖
由圖或者表中的數(shù)據(jù)可以看出,數(shù)據(jù)量小的時(shí)候,分布式算法時(shí)間要消耗得更多一些,這是因?yàn)椴⑿锌蚣鼙旧硪馁Y源和時(shí)間,并行帶來(lái)的性能還沒(méi)有彌補(bǔ)框架損失的性能。但隨著數(shù)據(jù)集的增大,很明顯,分布式的時(shí)間比單機(jī)版本消耗的時(shí)間要少,性能大約提升了四倍,而且性能的提升程度和集群的大小是成正比的。
4.3和MapReduce的二度人脈算法比較
在分布式好友推薦算法中,基于MapReduce的二度人脈好友推薦算法使用得較廣泛,F(xiàn)acebook和Hi5等OSNs就使用了該方法進(jìn)行好友推薦,來(lái)自于Facebook的數(shù)據(jù)科學(xué)家LarsBackstrom在eswc2011的報(bào)告[22]中介紹了他們是如何利用二度人脈的算法來(lái)為用戶推薦朋友。下面就BSP上的局部隨機(jī)游走算法和MapReduce上的二度人脈算法進(jìn)行比較。首先看兩個(gè)算法的推薦效果。采用MeanReciprocalRank(MRR)值作為測(cè)試指標(biāo),在原來(lái)的數(shù)據(jù)圖中刪除某頂點(diǎn)的10個(gè)好友,然后分別用這兩個(gè)算法試圖把刪去的10個(gè)好友推薦回來(lái),比較這十個(gè)好友的MRR值,結(jié)果如表4所示。
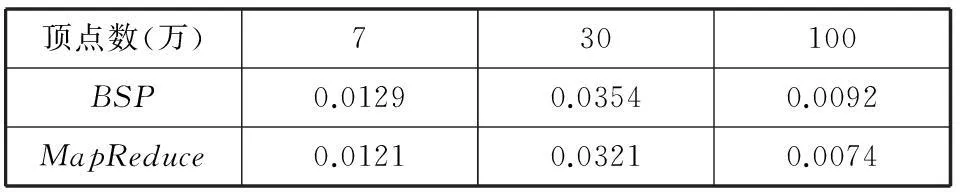
表4 MRR值對(duì)比
由于數(shù)據(jù)量很大,一個(gè)頂點(diǎn)的邊有很多,所以得到的MRR值非常小。由表4可以看出,BSP的MRR值比MapReduce的MRR值要大,可以得出結(jié)論,BSP上的局部隨機(jī)游走算法的推薦是更準(zhǔn)確的。
接下來(lái),比較兩者的計(jì)算時(shí)間,數(shù)據(jù)如表5所示。
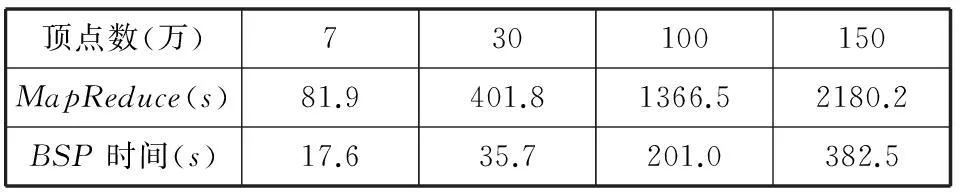
表5 兩個(gè)并行算法時(shí)間對(duì)比
圖7是表5中數(shù)據(jù)的折線圖顯示,橫坐標(biāo)是測(cè)試數(shù)據(jù)集頂點(diǎn)的個(gè)數(shù),單位為萬(wàn),縱坐標(biāo)是算法運(yùn)行的時(shí)間,單位為秒。
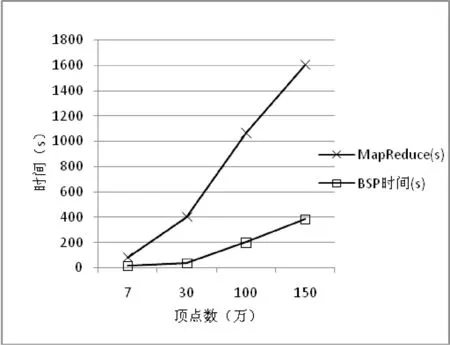
圖7 單機(jī)和并行算法時(shí)間對(duì)比圖
由圖7可以看出MapReduce上的二度人脈的性能遠(yuǎn)遠(yuǎn)不如BSP上的局部隨機(jī)游走算法的性能,主要原因是并行框架的差異,BSP適合迭代圖數(shù)據(jù)計(jì)算,中間消息采用消息傳遞,而不是通過(guò)文件系統(tǒng)存儲(chǔ)中間結(jié)果。而MapReduce框架的啟動(dòng)代價(jià)比較大,并且中間的結(jié)果是存儲(chǔ)在本地磁盤中,從而每次計(jì)算會(huì)產(chǎn)生大量的IO操作,所以抑制了性能。
5結(jié)語(yǔ)
本文首先提出了一種基于分布式圖計(jì)算框架的好友推薦方法,然后通過(guò)大量的實(shí)驗(yàn)證明了該方法的高效性和可擴(kuò)展性。實(shí)驗(yàn)中,首先和單機(jī)的局部隨機(jī)游走算法進(jìn)行了比較,證明了分布式的算法能夠帶來(lái)很大的性能提升,從而可以通過(guò)增加普通集群的方式來(lái)應(yīng)付大數(shù)據(jù)帶來(lái)的挑戰(zhàn)。接著又和現(xiàn)在流行的二度人脈算法進(jìn)行了比較,證明了本文提出的算法具有很高的應(yīng)用價(jià)值。為了進(jìn)一步提高本文方法的適用面,未來(lái)我們的工作主要集中在優(yōu)化好友推薦算法上。
參考文獻(xiàn)
[1]SocialNetworkService[EB/OL].http://newsroom.fb.com/Key-Facts.
[2]HaewoonKwak,ChanghyunLee,HosungPark,etal.WhatisTwitter,asocialnetworkornewsmedia?[C]//Proceedingsofthe19thInternationalConferenceonWorldWideWeb,2010:591-600.
[3]IdoGuy,InbalRonen,EricWilcox.Doyouknow?:recommendingpeopletoinviteintoyoursocialnetwork[C]//Proceedingsofthe14thinternationalconferenceonIntelligentuserinterfaces,February08-11,2009:77-86.
[4]MarkHall,EibeFrank,GeoffreyHolmes,etal.Thewekadataminingsoftware:anupdate[J].ACMSIGKDDexplorationsnewsletter,2009,11(1):10-18.
[5] 王兵輝.社交網(wǎng)絡(luò)中潛在好友推薦算法研究[D].云南大學(xué),2013.
[6] 俞琰,邱廣華.基于局部隨機(jī)游走的在線社交網(wǎng)絡(luò)朋友推薦算法[J].系統(tǒng)工程,2013,31(2):47-54.
[7] 佟婷婷,宋藝.小世界理論及其在Internet中的應(yīng)用[J].企業(yè)技術(shù)開(kāi)發(fā),2010,29(1):26-27.
[8] 楊婷.基于MapReduce的好友推薦系統(tǒng)的研究與實(shí)現(xiàn)[D].北京郵電大學(xué),2013.
[9] 楊長(zhǎng)春,楊晶,丁虹.一種新的新浪微博好友推薦算法[J].計(jì)算機(jī)應(yīng)用與軟件,2014,31(7):255-258,274.
[10] 于海群,劉萬(wàn)軍,邱云飛.基于用戶偏好的社會(huì)網(wǎng)絡(luò)二級(jí)人脈推薦研究[J].計(jì)算機(jī)應(yīng)用與軟件,2012,29(4):39-43.
[11]SilvaNB,TsangIR,CavalcantiGDC,etal.Agraph-basedfriendrecommendationsystemusinggeneticalgorithm[C]//Proceedingsof6thIEEEWorldCongressonComputationalIntelligence.Piscataway:IEEEPress,2010:233-239.
[12] 張龍昌,劉志晗,王攀,等.基于FOAF的分布式移動(dòng)SNS應(yīng)用[J].電信科學(xué),2010,26(5):88-92.
[13] 平衛(wèi)芳.Web數(shù)據(jù)挖掘中PageRank算法的研究與改進(jìn)[D].華東理工大學(xué),2014.
[14] 賀超波,湯庸,陳國(guó)華,等.面向大規(guī)模社交網(wǎng)絡(luò)的潛在好友推薦方法[J].合肥工業(yè)大學(xué)學(xué)報(bào):自然科學(xué)版,2013,36(4):420-424.
[15]MapReduce上實(shí)現(xiàn)二度人脈好友推薦算法[EB/OL].http://www.datalab.sinaapp.com/?=192.
[16] 張杰.PyGel:基于DPark的分布式圖計(jì)算引擎的研究與實(shí)現(xiàn)[D].華南理工大學(xué),2013.
[17] 蔡大威.基于Hadoop和Hama平臺(tái)的并行算法研究[D].浙江大學(xué),2013.
[18] 朱珠.基于Hadoop的海量數(shù)據(jù)處理模型研究和應(yīng)用[D].北京郵電大學(xué),2008.
[19]WeiZhou,BoLi,ZhangZhang,etal.Arbor:EfficientLarge-ScaleGraphDataComputingModel[C]//Proceedingsofthe15thIEEEInternationalConferenceonHighPerformanceComputingandCommunications,2013:300-307.
[20] 李金枝.基于RWR的圖像分割算法研究[D].重慶大學(xué),2010.
[21]PapadimitriouA,SyseonidisP,ManolopoulosY.Fastandaccuratelinkpredictioninsocialnetworkingsystems[J].JournalofSystemandSoftware,2012,85(9):2119-2132.
[22]DealingwithstructuredandunstructureddataatFacebook[EB/OL].http://videolectures.net/eswc2011_backstrom_facebook/.
STUDY ON A FRIEND RECOMMENDATION ALGORITHM BASED ON DISTRIBUTEDGRAPHCOMPUTINGFRAMEWORK
Zhao Masha1,2Zhou Wei1,2Zhang Hao3Han Jizhong1
1(Institute of Information Engineering,Chinese Academy of Science,Beijing 100093,China)2(University of Chinese Academy of Science,Beijing 100049,China)3(School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)
AbstractWith the rise and development of social networking sites, the user number show a growth trend in exponential level, in these massive data there contains a lot of valuable information, and to mine the useful information has become the focus of the scholars in their studies. The friend recommendation algorithm is one of the most important applications in data mining. To acquire better performance and higher scalability, it becomes a developing trend in both the academia and the industry to use a distributed platform in solving the large-scale friend recommendation. Currently, the friend recommendation algorithm based on MapReduce framework has been widely used because of its high scalability. However, the inefficient transmission of the intermediate data of MapReduce results in the performance deficiencies. To solve these problems, the paper proposes a distributed graph computing framework-based friend recommendation algorithm. In end of the paper, we give the evaluation of the proposed algorithm on a couple of real social network datasets, and the experimental results show that it is superior to the advanced friend recommendation algorithms of the industry, and its performance is about seven times than that of other algorithms under the circumstance of similar accuracy.
KeywordsFriend recommendationDistributed graph computing frameworkRandom walk
收稿日期:2014-10-09。國(guó)家自然科學(xué)基金項(xiàng)目(60903047);國(guó)家高技術(shù)研究發(fā)展計(jì)劃項(xiàng)目(2012AA01A401,2013AA013204);中國(guó)科學(xué)院先導(dǎo)專項(xiàng)(XDA06030200)。趙馬沙,碩士生,主研領(lǐng)域:大規(guī)模數(shù)據(jù)處理。周薇,博士生。張豪,碩士生。韓冀中,教授級(jí)高工。
中圖分類號(hào)TP3
文獻(xiàn)標(biāo)識(shí)碼A
DOI:10.3969/j.issn.1000-386x.2016.06.008

