復雜網絡中基于WCC的并行可擴展社團挖掘算法

亞森·艾則孜　李衛平　郭文強

1(新疆警察學院信息安全工程系　新疆 烏魯木齊 830013)2(鐵道警察學院公安技術系　河南 鄭州 450053)3(新疆財經大學計算機科學與工程學院　新疆 烏魯木齊 830013)

?

復雜網絡中基于WCC的并行可擴展社團挖掘算法

亞森·艾則孜1李衛平2郭文強3

1(新疆警察學院信息安全工程系新疆 烏魯木齊 830013)2(鐵道警察學院公安技術系河南 鄭州 450053)3(新疆財經大學計算機科學與工程學院新疆 烏魯木齊 830013)

摘要WCC(Weighted Community Clustering)通過復雜網絡中社團含有的三角數量來評價社團挖掘算法的性能。在原始的WCC算法中，需要在每次迭代中對所有的社團變化計算WCC值，因而計算量非常大。為了減小社團變化帶來的WCC計算量，提出一種并行可擴展的社團挖掘算法。對應用WCC進行社團評價的方法進行分析，提出一種包含預處理、初始劃分和劃分改進三個階段的并行社團挖掘算法。在劃分改進中，由于每次社團變化都需要計算大量的WCC提升，基于社團的統計量提出一種WCC近似計算方法。大量的真實數據集實驗表明，提出的社團挖掘算法與相關算法相比較，不僅社團檢測的準確性更高，而且具有更好的并行可擴展性。

關鍵詞復雜網絡社團挖掘并行算法可擴展性

0引言

近些年，復雜網絡分析已經成為數據挖掘領域的重要研究內容之一。復雜網絡分析可廣泛應用于社會學、生物學、信息科學等眾多領域[1,2]。在對這些復雜網絡進行分析的方法之中，社團挖掘是最重要的研究內容之一。在復雜網絡中，社團又被稱為聚類，是一組緊密相連的節點集合。社團內部節點的鏈接是緊密的，而不同社團節點之間的鏈接是松散的[3]。通過社團檢測，研究人員可以深入地了解網絡的結構信息[4]，網絡中節點之間的交互關系[5]，以及節點在網絡的進化中起到的作用[6]。

社團檢測往往需要很大的計算量，各種社團挖掘算法很難擴展到含有數十億邊規模的復雜網絡上。在2013年，Yang等[7]給出了真實網絡的基準測試數據集，并包含了數據集中社團的正確劃分。在該研究中，他們測試了不同最新社團挖掘算法[8-12]的執行時間，通過對比發現這些算法很難擴展到邊規模為數千條的復雜網絡。雖然BigClam[7]算法是針對大規模網絡設計的，但是該算法仍然不能處理含有20億條邊的Friendster數據集。此外，雖然Louvain算法[8]可以處理和Friendster數據集具有相同規模的數據集，但是社團挖掘的質量卻很低。

為了保持社團挖掘結果的準確性，同時提高應對海量數據的能力，本文提出一種兩階段的社團挖掘算法。在第一個階段，采用聚類系數作為啟發式方法獲得網絡的初始社團分割。在第二階段，通過對不同社團中的節點進行移動對第一階段得到的初始分割進行優化。在每次的社團調整過程中，通過增加社團的WCC[13]進行節點的移動。為了加速第二階段的社團調整過程，本文提出一種新的WCC評估器。該WCC評估器類似于傳統的WCC評價方法，但是卻有著更高的計算效率。

1基于WCC的社團挖掘算法

對于給定的無向無權圖G=(V,E)，本文的目標是通過最大化WCC值來挖掘圖中的不相交社團。本節首先描述了社團挖掘的WCC指標，然后基于WCC指標提出了相應的社團挖掘算法，接下來分析如何應用提出的算法對WCC值進行估計，最后分析了算法的復雜性。

1.1WCC指標

WCC是一種復雜網絡社團挖掘評價指標，該指標認為真實網絡中的社團結構往往含有大量的三角。由于社團是由緊密相連的節點組成，那么這些節點構成三角的概率要相對較高，WCC應用該特征對圖的節點集合劃分(即社團劃分)進行量化。

給定圖G=(V,E)，節點x以及社團C，令t(x,C)表示x與C中節點構成的三角的個數，vt(x,C)表示C中能與x構成三角的節點的個數，那么將節點x與社團C的凝聚水平WCC(x,C)進行如下定義：

(1)

基于式(1)，社團C的WCC的計算公式為：

(2)

給定集合C，WCC(C)是C中所有節點的WCC的值的平均值。給定圖分割P={C1,C2,…,Cn}，并且C1∩…∩Cn，那么P的WCC為該劃分中所有社團的WCC的加權平均值，其計算公式如下：

(3)

1.2社團挖掘算法

為了對圖G進行劃分得到P，本文提出一種最大化WCC(P)社團挖掘算法。該算法包含數據的預處理、初始劃分和劃分改進三部分。

1.2.1預處理

在圖G=(V,E)的加載時，進行如下的預處理操作：對于G中的每條邊e∈E，計算e可以構成的不同三角的個數，并移除那些不能構成三角的邊。

在預處理結束后，得到的圖為G′。預處理操作存在如下兩個優點：(1)WCC的計算并不依賴于這些邊，因而可以提高計算效率；(2) 通過移除不能構成三角的邊可以大幅壓縮圖的存儲空間，從而節省內存開銷。

1.2.2初始劃分

該階段對預處理得到的圖G′進行初始劃分，其基本思想是：節點的聚類系數越大，那么該節點與鄰居節點形成的三角個數越多，因而該節點的鄰居節點形成三角的概率也越大。依據式(1)，如果節點的聚類系數越大，那么與該節點同屬于一個社團的那些鄰居節點的WCC概率越大。

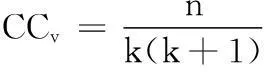
1.2.3劃分改進

在得到初始劃分后，需要對劃分進行不斷改進直到找到最優劃分。在劃分改進階段，使用爬山搜索策略。在每次迭代中，通過一系列變換操作(3種)，依據原有的劃分得到WCC值更高的劃分。迭代終止的條件為迭代前后劃分的WCC值變化小于閾值，或者迭代到一定的次數。

在每次迭代中，對于圖中的所有節點v∈V，在下列三種變換操作中選取一個最佳變換，使得變化后得到的劃分較變換之前是最優的：

? 不進行變換：使節點v處于原來的劃分C中。

? 移除：將節點v從原來的劃分C中移除并作為單體社團。用WCCR(v,C)來表示移除操作得到的WCC提升值，令P={C1,…,C,…,Ck}為原來的劃分，P'={C1,…,C′,…,Ck,{v}}為變換后的劃分，對于給定的圖G=(V,E)，WCCR(v,C)的計算公式如下：

WCCR(v,C)=WCC(P′)-WCC(P)=-WCCI(v,C′)

(4)

其中C=C′∪{v}。

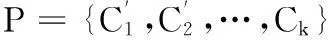
WCCT(v,C1,C2)=WCC(P′)-WCC(P)

(5)

在每次迭代中，由于每個節點之間的變換操作是相互獨立的，所以可以并行地運行，因此可以大大提高算法的運行效率。

1.3WCCI值估計

WCC值的精確計算需要知道目標節點及其鄰居節點構成的三角個數，對于含有d個鄰居的節點，該操作的計算復雜度為O(d2)。由于網絡節點度數的冪率分布特征，在并行計算模式下，極少數度數大的節點的計算時間往往影響著整個算法的運行效率。此外，在每次迭代過程中都需要計算WCC的提高值WCCI，因此WCCI的計算性能決定著算法的整體效率。為了加速WCCI的計算，本文提出了一種近似計算方法，該方法的基本思想如圖1所示。

圖1　WCCI的計算示意圖

當節點v被加入到社團C時，WCC值的提高值為WCCI。對于節點v，僅僅考慮C中與v相連的節點的個數din。對于每個社團C，記錄如下的統計量：節點個數r，邊的密度δ，社團邊界的邊的個數b。同時，保存著圖G的聚類系數ω(常數)。基于上述統計量，應用如下公式得到WCCI的估計值：

(6)

其中θ1、θ2和θ3分別為相應變量的系數，并且和為1。

2實驗結果與分析

本節通過大量的真實數據集實驗對算法的性能進行了評估。

2.1數據集與性能指標

本文的實驗采用Stanford提供的公開網絡數據集SNAP(http://snap.stanford.edu)，其中包括Amazon、Dblp、Youtube、LiveJournal、Orkut和Friendster六個網絡數據集。這些數據集的基本統計信息如表1所示。

表1　數據集基本信息

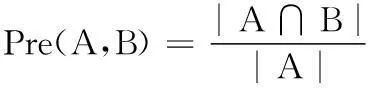
2.2實驗結果

在實驗中，我們將本文提出的可擴展的社團檢測算法記為scd，并將該算法與walktrap[8]、louvain[9]、oslom[10]、infoman[11]和bigclam[12]五種社團挖掘算法進行了對比。

首先，應用六種社團挖掘算法對上述的6個網絡數據集進行社團檢測，并對比了社團挖掘結果的準確性。圖2和圖3分別為六種算法在不同數據集上的F1值和NMI對比圖。在這兩個柱狀圖中，如果數據集對應的柱為空，說明相應算法的F1值或NMI值幾乎為0。從這兩幅圖中可以看出，除了walktrap和louvain兩種算法在Amazon數據集上的NMI值大于scd算法外，scd算法在其他數據集上的NMI和F1值都高于其他算法。這說明本文提出的社團挖掘算法對于不同類型的網絡都具有更好的社團檢測性能。

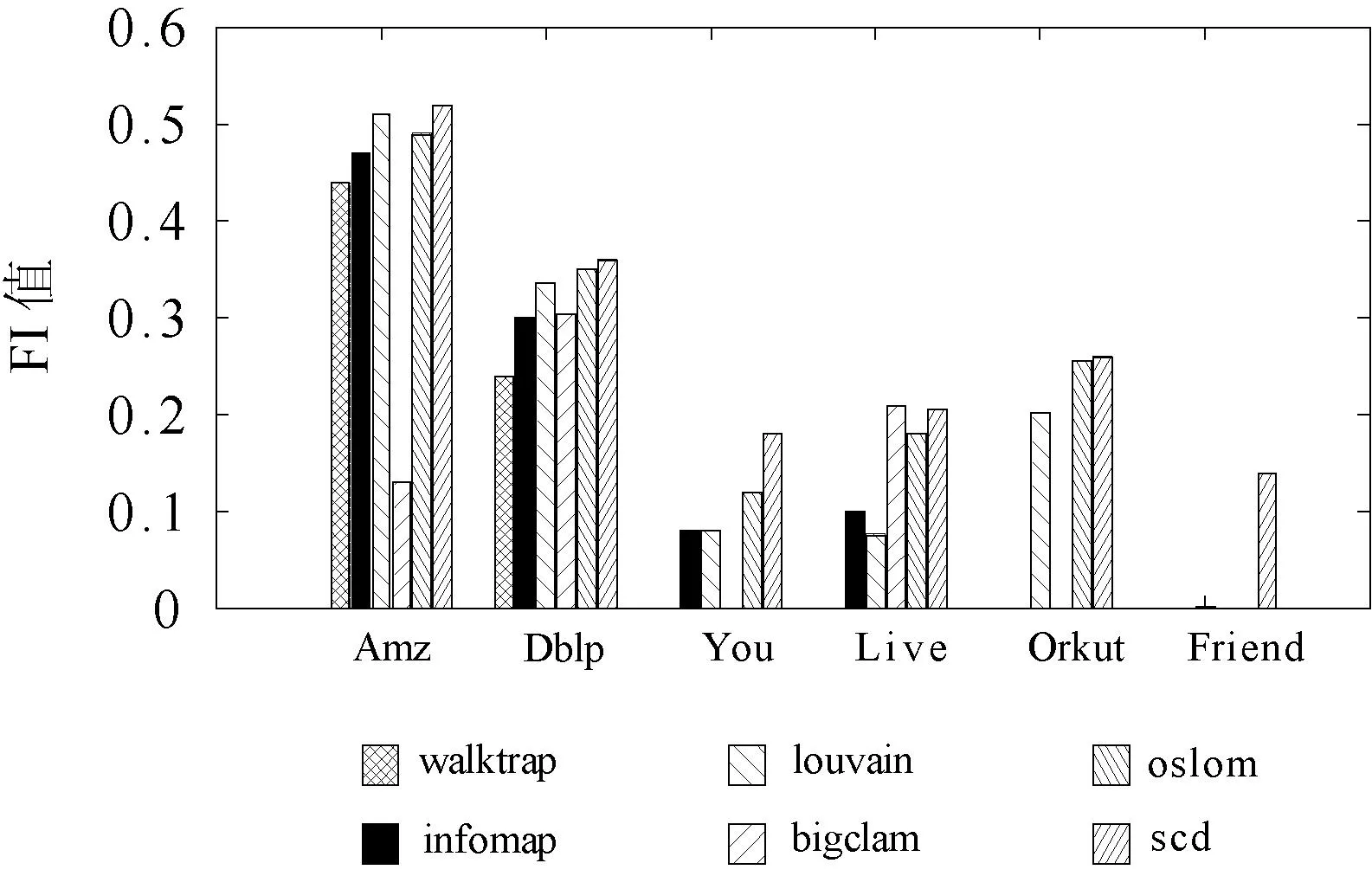
圖2　算法的F1值對比

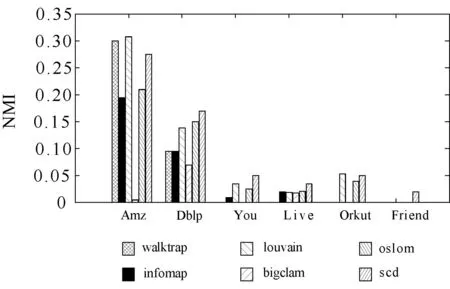
圖3　算法的NMI對比

其次，通過實驗對比了六種算法在這些數據集上的執行效率，實驗結果如圖4所示。在該組實驗中，我們省略了那些準確性幾乎為0的算法，令相應的柱值為空。從該圖可以看出本文提出的算法的執行時間在6個數據集上的執行時間都是最短的，而louvain算法次之。我們對算法進行并行化，分析了scd算法在不同數量線程下的運行效率。在圖5中，橫軸表示算法的線程數量，縱軸為算法的運行時間，由于算法在單線程下的運行時間大于1秒，為了更好地對實驗結果進行展示并在1秒處進行了截斷。從圖5可以看出，由于對scd算法進行了并行化，因此算法的執行時間明顯減少了，并且在LiveJournal、Orkut和Friendster三個數據集上的并行效果要優于其他三個數據集。

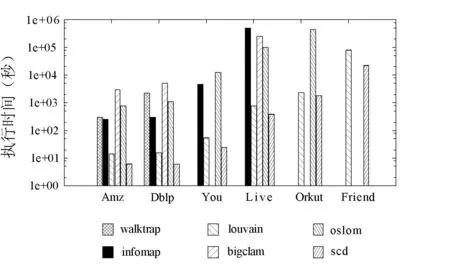
圖4　算法的執行效率對比

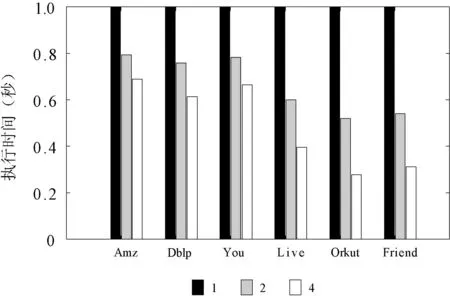
圖5　scd算法的執行時間評估

最后，我們進一步分析了scd算法的并行化性能。圖6為scd算法在不同算法下的運行時間，橫軸表示網絡中邊的規模，縱軸為scd算法在相應網絡中進行社團挖掘所需的執行時間。圖6表明當網絡中邊的數量不斷增加時，scd算法的執行時間近似呈線性增長，因而可以認定scd算法具有更好的并行化性能，其執行時間隨著網絡規模的增長具有很好的可擴展性。

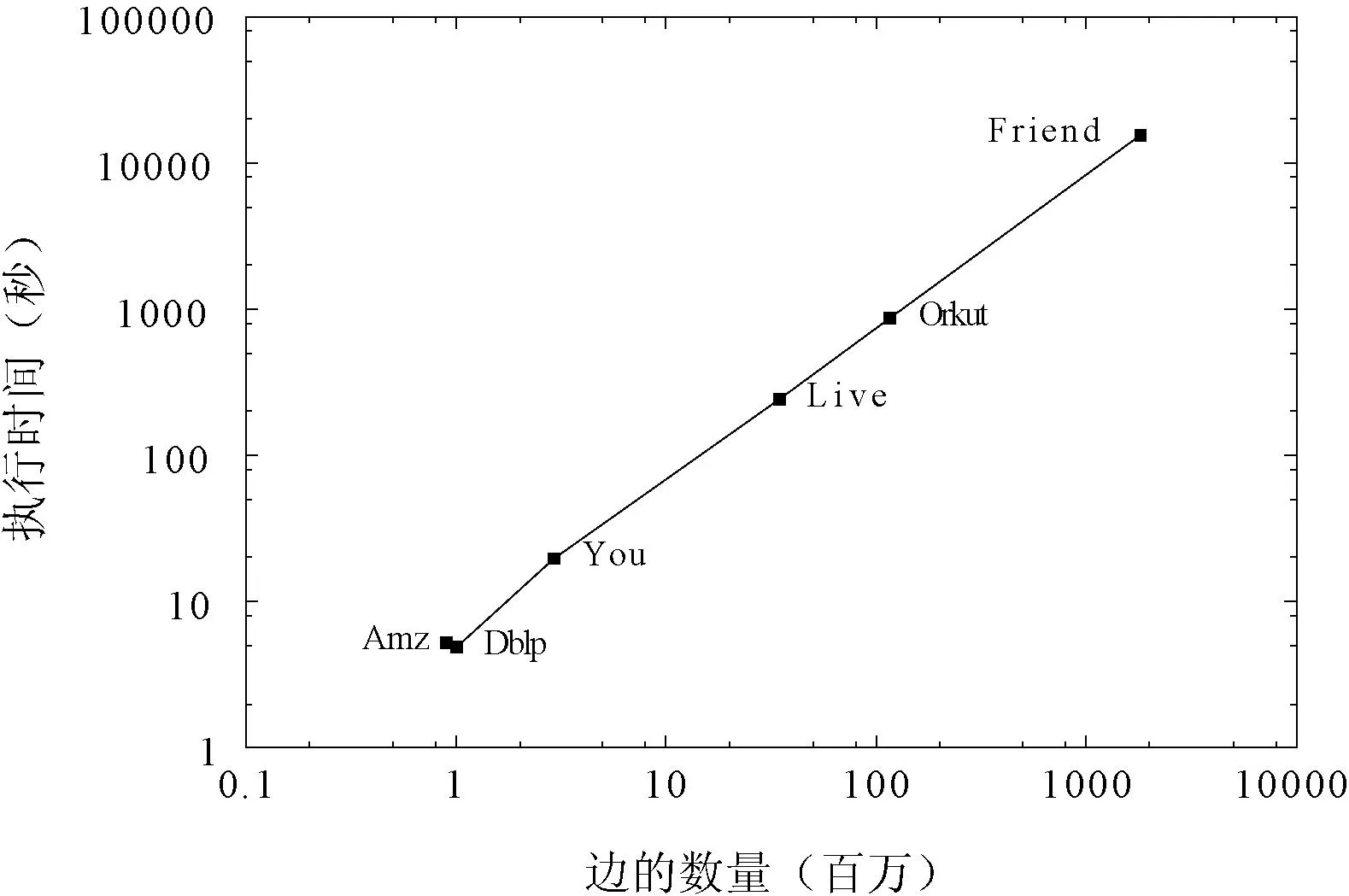
圖6　scd算法的可擴展性分析

3結語

社團挖掘是復雜網絡的重要研究內容之一。通過社團檢測，可以深入了解網絡的結構信息，網絡中節點之間的交互關系，以及節點在網絡的進化中起到的作用。為了減小社團變化帶來的WCC計算量，本文提出了一種并行可擴展的社團挖掘算法。對應用WCC進行社團評價的方法進行了分析，提出了一種包含預處理、初始劃分和劃分改進三個階段的并行社團挖掘算法。在劃分改進中，由于每次社團變化都需要計算大量的WCC提升，本文基于社團的統計量提出一種WCC近似計算方法。大量的真實數據集實驗表明，本文提出的社團挖掘算法與相關算法相比較，不僅社團檢測的準確性更高，而且具有更好的并行可擴展性。

參考文獻

[1] 汪小帆,李翔,陳關榮.復雜網絡理論及其應用[M].清華大學出版社有限公司,2006.

[2]BoccalettiS,LatoraV,MorenoY,etal.Complexnetworks:Structureanddynamics[J].Physicsreports,2006,424(4):175-308.

[3] 駱志剛,丁凡,蔣曉舟,等.復雜網絡社團發現算法研究新進展[J].國防科技大學學報,2011,33(1):47-52.

[4] 汪小帆.復雜網絡中的社團結構分析算法研究綜述[J].復雜系統與復雜性科學,2005,2(3):1-12.

[5] 王林,戴冠中.基于復雜網絡社區結構的論壇熱點主題發現[J].計算機工程,2008,34(11):214-216.

[6] 呂金虎.復雜網絡的同步:理論,方法,應用與展望[J].力學進展,2008,38(6):713-722.

[7]YangJ,LeskovecJ.Overlappingcommunitydetectionatscale:anonnegativematrixfactorizationapproach[C]//ProceedingsofthesixthACMinternationalconferenceonWebsearchanddatamining.ACM,2013:587-596.

[8]BlondelVD,GuillaumeJL,LambiotteR,etal.Fastunfoldingofcommunitiesinlargenetworks[J].JournalofStatisticalMechanics:TheoryandExperiment,2008,28(10):100-108.

[9]AhnYY,BagrowJP,LehmannS.Linkcommunitiesrevealmultiscalecomplexityinnetworks[J].Nature,2010,466(7307):761-764.

[10]BagrowJP.Communitiesandbottlenecks:Treesandtreelikenetworkshavehighmodularity[J].PhysicalReviewE,2012,85(6):66-78.

[11]FortunatoS,BarthelemyM.Resolutionlimitincommunitydetection[J].ProceedingsoftheNationalAcademyofSciences,2007,104(1):36-41.

[12]LancichinettiA,FortunatoS.Communitydetectionalgorithms:acomparativeanalysis[J].PhysicalreviewE,2009,80(5):056117.

[13]Prat-PérezA,Dominguez-SalD,BrunatJM,etal.Shapingcommunitiesoutoftriangles[C]//Proceedingsofthe21stACMinternationalconferenceonInformationandknowledgemanagement.ACM,2012:1677-1681.

[14]LancichinettiA,FortunatoS,KertészJ.Detectingtheoverlappingandhierarchicalcommunitystructureincomplexnetworks[J].NewJournalofPhysics,2009,11(3):33-45.

WCC-BASED PARALLEL AND SCALABLE COMMUNITY MINING ALGORITHMINCOMPLEXNETWORKS

Yasen·Aizezi1Li Weiping2Guo Wenqiang3

1(Department of Information Security and Engineering,Xinjiang Police College,Urumqi 830013,Xinjiang,China)2(Department of Police Technology,Railway Police College,Zhengzhou 450053,Henan,China)3(School of Computer Science and Engineering,Xinjiang University of Finance and Economic, Urumqi 830013,Xinjiang,China)

AbstractWeighted community clustering (WCC) evaluates the performance of community mining algorithms according to triangles number of a community in complex networks. In primitive WCC algorithm it has the need to compute WCC scores for all community changes in each iteration, therefore the computation burden is very heavy. In order to minimise WCC computation brought about by communities change, this paper proposes a parallel and scalable community mining algorithm. We analysed the methods of community evaluation using WCC, and proposed a parallel community mining algorithm including three stages of preprocessing, initial partitioning and partition refinement. During the process of partition refinement, since every change in community needs much computation for WCC improvements, so we proposed a WCC approximated computation algorithm based on the statistics of community. Massive experiments on real datasets show that, the proposed community mining algorithm is more accurate and has better scalability than related works.

KeywordsComplex networksCommunity miningParallel algorithmScalability

收稿日期：2014-12-02。國家自然科學基金項目(61163066，6090 2074)；新疆維吾爾自治區高校科研計劃科學研究重點項目(XJEDU 2013134)；國家社會科學基金項目(13CFX055)；河南省教育廳科學技術研究重點項目(14A520011)。亞森·艾則孜，教授，主研領域：信息安全，自然語言處理，信息檢索。李衛平，副教授。郭文強，教授。

中圖分類號TP391

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.06.009