基于Pairwise排序?qū)W習(xí)的因子分解推薦算法
周俊宇 戴月明 吳定會(huì)
(江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院 江蘇 無(wú)錫 214122)
?
基于Pairwise排序?qū)W習(xí)的因子分解推薦算法
周俊宇戴月明吳定會(huì)
(江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院江蘇 無(wú)錫 214122)
摘要針對(duì)基于內(nèi)存的協(xié)同過(guò)濾推薦算法存在推薦列表排序效果不佳的問(wèn)題,提出基于Pairwise排序?qū)W習(xí)的因子分解推薦算法(簡(jiǎn)稱(chēng)Pairwise-SVD推薦算法)。新算法將因子分解的預(yù)測(cè)結(jié)果作為排序?qū)W習(xí)算法的輸入,把排序問(wèn)題轉(zhuǎn)化成分類(lèi)問(wèn)題使用排序?qū)W習(xí)理論進(jìn)行排序產(chǎn)生推薦列表。實(shí)驗(yàn)結(jié)果表明相比基于內(nèi)存的協(xié)同過(guò)濾推薦算法,Pairwise-SVD推薦算法的排序效果更佳。其在指標(biāo)Kendall-tau上提高了近一倍,在指標(biāo)MRR上提高了近30%,且在指標(biāo)MAP上也有小幅提高。
關(guān)鍵詞Pairwise因子分解協(xié)同過(guò)濾分類(lèi)排序?qū)W習(xí)
0引言
隨著大數(shù)據(jù)時(shí)代的到來(lái),信息過(guò)載問(wèn)題成為人們?nèi)找骊P(guān)注解決的難題。用戶迫切希望可以從海量數(shù)據(jù)當(dāng)中發(fā)現(xiàn)對(duì)于自己有用的信息,針對(duì)這一需求研究人員提出了推薦系統(tǒng)這一研究課題。
推薦系統(tǒng)主要以推薦列表的形式給用戶推送信息也稱(chēng)為T(mén)op-N推薦。基于內(nèi)存的協(xié)同過(guò)濾推薦算法主要有基于用戶的協(xié)同過(guò)濾推薦算法和基于物品的協(xié)同過(guò)濾推薦算法。這類(lèi)算法的特點(diǎn)是通過(guò)相似度計(jì)算來(lái)給用戶推送其可能感興趣的物品信息。不過(guò)這類(lèi)算法也有排序效果不佳的不足,主要是其沒(méi)有考慮推薦物品與用戶的相關(guān)度。為提高推薦算法的預(yù)測(cè)精度,學(xué)術(shù)界對(duì)評(píng)分預(yù)測(cè)問(wèn)題展開(kāi)了大量的研究。其中典型的算法是以因子分解算法為代表的一系列改進(jìn)算法。下面將介紹推薦系統(tǒng)領(lǐng)域的一些研究情況。
YueShi等[1]人提出了一種將排序?qū)W習(xí)融入矩陣分解的協(xié)同過(guò)濾推薦算法。其排序?qū)W習(xí)算法的類(lèi)型是列表級(jí)排序,通過(guò)優(yōu)化列表級(jí)排序的損失函數(shù)來(lái)進(jìn)行算法的性能優(yōu)化。不過(guò)這種算法雖然效果很好,但是它只從損失函數(shù)的角度進(jìn)行優(yōu)化所以這種算法的實(shí)用性不是很強(qiáng)。
SeanM.McNee等[2]人提出了新的觀點(diǎn),即僅僅通過(guò)改良預(yù)測(cè)精度是不足以說(shuō)明推薦效果的好壞。雖然基于評(píng)分預(yù)測(cè)的改進(jìn)大大提高了評(píng)價(jià)指標(biāo)的結(jié)果。但在實(shí)際的推薦系統(tǒng)中效果卻不明顯,因?yàn)橛脩粼趯?shí)際情況下并不會(huì)真的喜歡預(yù)測(cè)精度高的物品。
YueShi等[3]人提出了CLiMF協(xié)同過(guò)濾推薦算法,該算法優(yōu)化的主要目標(biāo)是MRR。該指標(biāo)反映了用戶最關(guān)心的物品在推薦列表中的排序位置,它是信息檢索領(lǐng)域中的重要指標(biāo)。CLiMF算法在原來(lái)的協(xié)同推薦算法的基礎(chǔ)之上考慮了排序性能的優(yōu)化問(wèn)題,其在MRR指標(biāo)上的表現(xiàn)較好。
ShuziNiu等[4]人提出了一種新的Top-N推薦算法,并將其命名為FocusedRank算法。該算法有效地降低了原有Top-N算法的時(shí)間復(fù)雜度,從O(n)降低為O(nlogn)。并且針對(duì)新的算法提出了新的評(píng)價(jià)準(zhǔn)則k-NDCG和k-ERR。
雖然排序?qū)W習(xí)理論在信息檢索領(lǐng)域已經(jīng)有了大量的研究成果,但是將排序?qū)W習(xí)理論用于推薦系統(tǒng)的研究卻少之又少。本文在前人工作的基礎(chǔ)之上展開(kāi),提出將Pairwise排序?qū)W習(xí)理論加入到因子分解推薦算法當(dāng)中,并采用Rank-SVM方法具體實(shí)現(xiàn)Pairwise排序。最后通過(guò)在三種不同類(lèi)型的排序指標(biāo)上進(jìn)行對(duì)比實(shí)驗(yàn)來(lái)驗(yàn)證本文提出的算法的性能優(yōu)勢(shì)。
1理論基礎(chǔ)
這節(jié)主要闡述構(gòu)成本文算法的理論基礎(chǔ)。主要從兩個(gè)方面進(jìn)行介紹,分別是Bias-SVD算法、排序?qū)W習(xí)理論等內(nèi)容。
1.1Bias-SVD算法
本文提出的Pairwise-SVD推薦算法借鑒了Bias-SVD推薦算法的思想。所以先簡(jiǎn)要地闡述一下Bias-SVD算法的思想。
為了預(yù)測(cè)用戶物品評(píng)分矩陣當(dāng)中的空缺項(xiàng)需要把評(píng)分矩陣進(jìn)行分解,分解后的矩陣表示成如下的形式:
(1)
這里矩陣R代表的是用戶物品評(píng)分矩陣,P和Q是分解后的兩個(gè)降維矩陣,P矩陣代表的是用戶的特征,Q矩陣代表的是物品的特征。這里可以通過(guò)在訓(xùn)練集的觀察值上利用最小化均方根誤差來(lái)學(xué)習(xí)P矩陣和Q矩陣[5]。通過(guò)這種方法可以把上述矩陣表示成如下的形式:
(2)
為了進(jìn)一步提高預(yù)測(cè)精度,Bias-SVD算法在上面的矩陣分解的基礎(chǔ)之上加入了三個(gè)偏置項(xiàng),把上面的公式改變成了如下的形式:
(3)
其中,μ表示訓(xùn)練數(shù)據(jù)集當(dāng)中評(píng)分的平均情況。因?yàn)椴煌臄?shù)據(jù)集評(píng)分分布情況有很大的不同。比如說(shuō)有的數(shù)據(jù)集評(píng)分普遍偏高,而有的數(shù)據(jù)集評(píng)分普遍偏低。所以數(shù)據(jù)集的評(píng)分均值對(duì)預(yù)測(cè)有很大的干擾影響,這里為平衡該影響而引入評(píng)分均值這一項(xiàng)。
bu表示用戶的評(píng)分偏置項(xiàng)。由于不同用戶打分的尺度不相同,會(huì)造成對(duì)于同一物品相似用戶的打分產(chǎn)生巨大的偏差。例如有的用戶比較苛刻打分普遍偏低,而有的用戶尺度寬松打分普遍較高。通過(guò)加入這一偏置項(xiàng)就可均衡這種情況提高預(yù)測(cè)精度。
bi表示物品偏置項(xiàng)。該項(xiàng)表示物品的受歡迎程度,因?yàn)橛械奈锲繁容^熱門(mén)所以評(píng)分一般都很高,而有的物品比較冷門(mén)打分普遍偏低。通過(guò)引入這一項(xiàng)可以懲罰熱門(mén)物品,并平衡冷門(mén)物品。
為了學(xué)習(xí)公式中的各個(gè)參數(shù),使用最小二乘法來(lái)定義損失函數(shù)。得出Bias-SVD算法的損失函數(shù)如下所示:
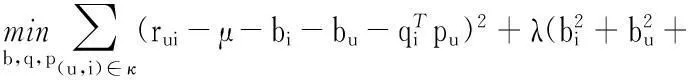
(4)
在確定了損失函數(shù)之后可以通過(guò)隨機(jī)梯度下降法學(xué)習(xí)損失函數(shù)中的各參數(shù)。下面列出隨機(jī)梯度下降學(xué)習(xí)的策略:
bu←bu+γ·(eui-λ·bu)bi←bi+γ·(eui-λ·bi)pu←pu+γ·(eui·qi-λ·pu)qi←qi+γ·(eui·pu-λ·qi)
(5)
通過(guò)上面的學(xué)習(xí)策略就可以求得各個(gè)參數(shù)的結(jié)果。
1.2排序?qū)W習(xí)理論
所謂排序?qū)W習(xí)理論即將信息檢索領(lǐng)域中的排序問(wèn)題轉(zhuǎn)化成機(jī)器學(xué)習(xí)問(wèn)題,以此期望獲得更好的排序結(jié)果。一般的排序?qū)W習(xí)問(wèn)題可用如圖1的流程來(lái)進(jìn)行說(shuō)明。
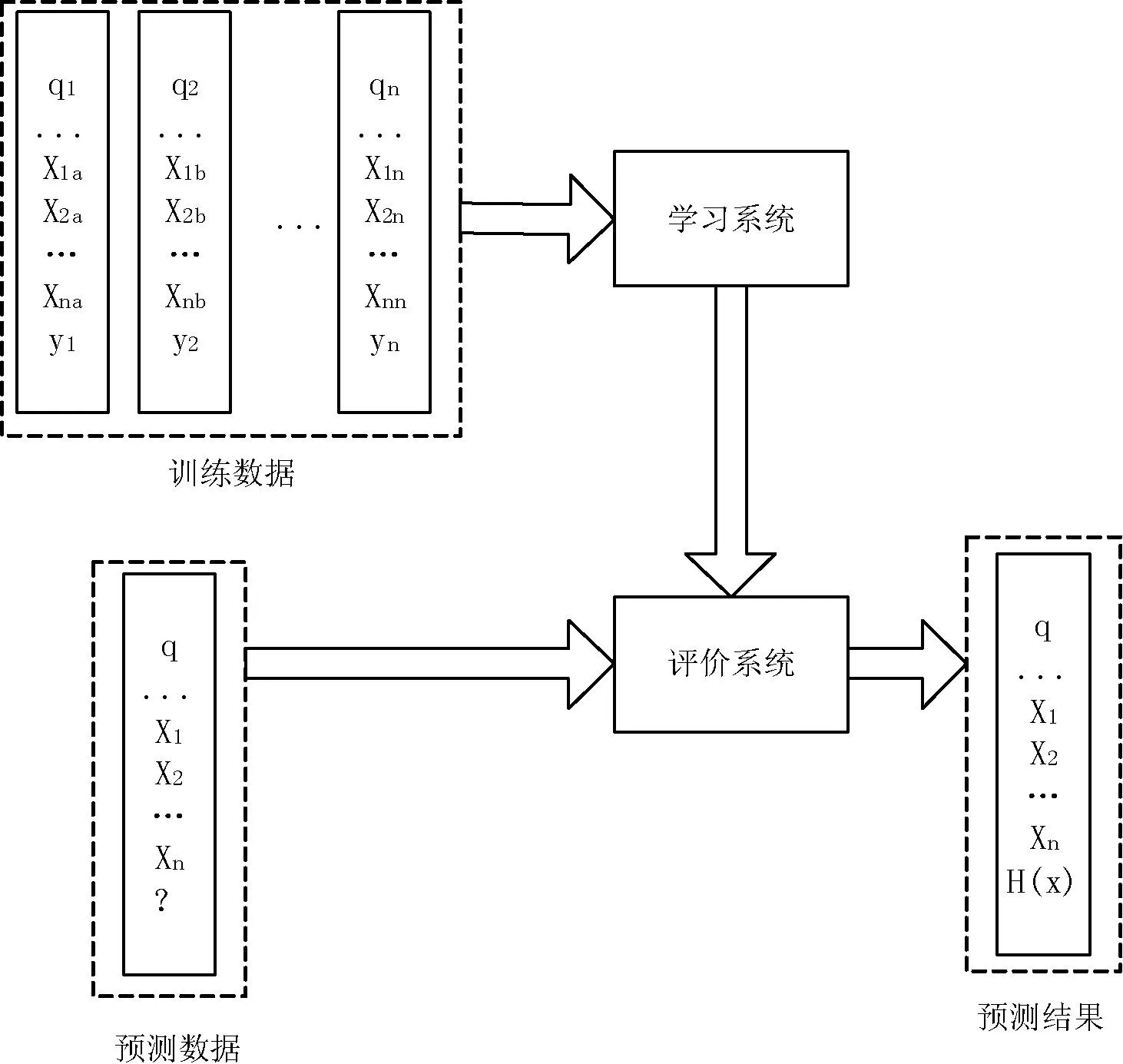
圖1 排序?qū)W習(xí)算法流程圖
從圖1可以看出排序?qū)W習(xí)是一種有監(jiān)督學(xué)習(xí),所以它需要訓(xùn)練集來(lái)構(gòu)造模型。舉例來(lái)說(shuō),在信息檢索的過(guò)程當(dāng)中一個(gè)訓(xùn)練集包含有n個(gè)查詢(xún)(在圖中用q1到qn表示)。相應(yīng)的與查詢(xún)相關(guān)的文檔可以用x1到xm來(lái)表示。這里的m表示對(duì)于某一個(gè)查詢(xún)返回的文檔個(gè)數(shù)。圖中的模型的獲得可以通過(guò)一個(gè)具體的學(xué)習(xí)算法取得(比如組合特征方法)。通過(guò)這一學(xué)習(xí)算法可以使模型盡可能準(zhǔn)確地預(yù)測(cè)出訓(xùn)練集的標(biāo)簽。在進(jìn)行測(cè)試的時(shí)候只需要運(yùn)用訓(xùn)練好的模型就可以產(chǎn)生推薦列表。
根據(jù)輸入數(shù)據(jù)的格式不同,通常情況下排序?qū)W習(xí)算法主要分為三大類(lèi)。有基于點(diǎn)的排序算法(Pointwise),基于對(duì)的排序算法(Pairwise),基于列表的排序算法(Listwise)[6]。
本文所采用的排序方法屬于基于對(duì)的排序方法,故下面將主要闡述基于對(duì)的排序方法的主要思想和實(shí)現(xiàn)手段。
基于對(duì)的排序方法不關(guān)心單個(gè)文檔的順序,其主要關(guān)注的是文檔對(duì)的分類(lèi)問(wèn)題。也就是說(shuō)基于對(duì)的排序方法把排序問(wèn)題轉(zhuǎn)化為二元分類(lèi)問(wèn)題。如果每一個(gè)文檔對(duì)都能正確的分類(lèi)那么也就可以得出正確的排列順序。所以基于對(duì)的排序方法的主要目標(biāo)是盡可能快地縮小分類(lèi)的誤差。
基于對(duì)的排序方法實(shí)現(xiàn)有很多的方法,比如神經(jīng)網(wǎng)絡(luò)、感知器、boosting、Rank-SVM方法等。由于本文的排序?qū)W習(xí)方法通過(guò)Rank-SVM實(shí)現(xiàn)所以下面主要講解Rank-SVM方法的主要思路。
1.3Rank-SVM方法
Rank-SVM方法采用支持向量機(jī)模型解決分類(lèi)問(wèn)題。Rank-SVM方法在訓(xùn)練數(shù)據(jù)集上構(gòu)造數(shù)據(jù)樣本對(duì)S={(xi,xj),zi},其中xi與xj表示針對(duì)某一個(gè)查詢(xún)返回的文檔。如果(xi,xj)是正樣本對(duì)則zi的值表示為+1,如果(xi,xj)是負(fù)樣本對(duì)則zi的值表示為-1。Rank-SVM方法的數(shù)學(xué)表達(dá)如下所示[7]:
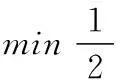
(6)
從上面的數(shù)學(xué)公式可以看出Rank-SVM方法與一般的SVM方法非常接近。但所不同的是兩種方法的約束條件有一定的差別。SVM方法的約束條件是基于單個(gè)的樣本點(diǎn)構(gòu)造的,而Rank-SVM方法的約束條件基于樣本對(duì)構(gòu)造。并且Rank-SVM方法的損失函數(shù)定義為樣本對(duì)上的Hinge損失。舉例來(lái)說(shuō),有一個(gè)查詢(xún)q,如果其標(biāo)簽當(dāng)中的文檔xu比xv相關(guān)。并且如果兩條支持向量的最大間隔大于1,還滿足條件wTxu>wTxv的條件,則其損失函數(shù)為0,否則為Hinge損失的0到1的上界。
圖2、圖3用通俗的方法說(shuō)明Rank-SVM方法的基本思想。
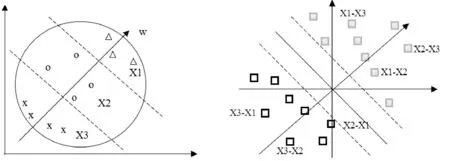
圖2 針對(duì)某一個(gè)用戶的查詢(xún) 圖3 基于成對(duì)排序的Rank-SVM分類(lèi)
圖2中的橢圓形表示一個(gè)用戶的查詢(xún),這里我們選取一個(gè)用戶的查詢(xún)做成對(duì)排序(在推薦系統(tǒng)里這可以看作是針對(duì)一個(gè)用戶的推薦列表)。
圖3表示將一個(gè)用戶的查詢(xún)信息轉(zhuǎn)化成成對(duì)信息后用Rank-SVM分類(lèi)的結(jié)果。這里有兩個(gè)類(lèi)別+1和-1。其中+1代表正相關(guān),-1代表負(fù)相關(guān)。舉例來(lái)說(shuō)(X3-X1)表示這個(gè)數(shù)據(jù)分類(lèi)為-1也就是負(fù)相關(guān),也就是說(shuō)用戶不希望X3文檔排列在X1文檔的前面。所以文檔對(duì)(X1-X3)分類(lèi)為+1就是正相關(guān)。
2Pairwise-SVD算法
2.1算法描述
本文提出的算法在Bias-SVD算法的基礎(chǔ)之上進(jìn)行改進(jìn),把只能處理單個(gè)數(shù)據(jù)的Bias-SVD算法改造成可以處理成對(duì)數(shù)據(jù)的Pairwise-SVD算法。
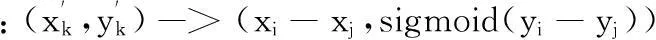
這樣接下來(lái)就可以把Bias-SVD算法的評(píng)分預(yù)測(cè)公式進(jìn)行如下的改造:
(7)
這里簡(jiǎn)要解釋一下上面的數(shù)學(xué)公式的含義。公式的左半部分表示的是一個(gè)偏序關(guān)系,即對(duì)于用戶u我們把物品i排列在物品j的前面這樣的一個(gè)偏序關(guān)系[8]。等式的右邊是改造的打分函數(shù),即針對(duì)這樣的偏序關(guān)系依照等式右邊的方法進(jìn)行打分。在等式的右邊添加sigmoid函數(shù)是為了做歸一化處理,使最終的打分函數(shù)的取值落在-1到1之間。
下面闡述一下Pairwise-SVD算法的具體執(zhí)行步驟:
(1) 我們要把數(shù)據(jù)集中的數(shù)據(jù)進(jìn)行Pairwise化處理,因?yàn)橹挥羞@樣才能進(jìn)行后續(xù)的工作。
(2) 將Pairwise化后的數(shù)據(jù)集進(jìn)行分割,分割為訓(xùn)練集合測(cè)試集。
(3) 在訓(xùn)練集上利用隨機(jī)梯度下降算法訓(xùn)練Pairwise-SVD算法的模型。
(4) 判斷模型訓(xùn)練是否終止不終止則返回步驟(3)。
(5) 如果訓(xùn)練終止,在測(cè)試集上面測(cè)試訓(xùn)練好的模型的效果。
(6) 如果訓(xùn)練好的模型的效果達(dá)標(biāo),用該模型產(chǎn)生的信息作為Rank-SVM方法的輸入。
(7) 訓(xùn)練Rank-SVM模型。
(8) 判斷Rank-SVM模型訓(xùn)練是否終止如不終止返回步驟(7)。
(9) 利用Rank-SVM方法進(jìn)行排序產(chǎn)生推薦列表。
(10) 評(píng)估推薦效果的好壞情況。
2.2Pairwise-SVD算法程序流程圖
下面我們通過(guò)一個(gè)流程圖詳細(xì)講述Pairwise-SVD算法在計(jì)算機(jī)當(dāng)中執(zhí)行的每一個(gè)步驟。如圖4所示。
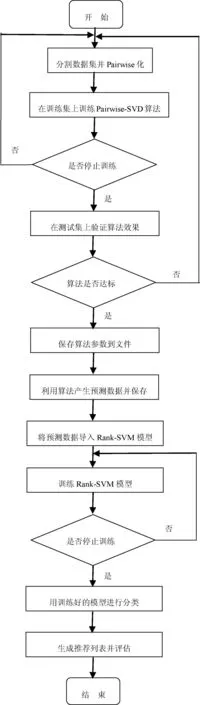
圖4 算法程序流程圖
3實(shí)驗(yàn)驗(yàn)證
3.1實(shí)驗(yàn)用數(shù)據(jù)集
本文實(shí)驗(yàn)所采用的數(shù)據(jù)集是GroupLens研究小組的MovieLens100KB數(shù)據(jù)集。該數(shù)據(jù)集包含943個(gè)用戶對(duì)于1682部電影的評(píng)分?jǐn)?shù)據(jù)。并且每名用戶至少評(píng)價(jià)20部以上的電影。
3.2評(píng)價(jià)指標(biāo)
本文主要采用三種基于排序的評(píng)價(jià)指標(biāo)評(píng)價(jià)推薦效果的好壞。它們分別是Kendall-tau,MRR和MAP。
其中Kendall-tau評(píng)價(jià)指標(biāo)用于比較用戶喜歡的物品列表與推薦給用戶的物品列表的關(guān)系。Kendall-tau指標(biāo)越高說(shuō)明推薦的物品與用戶喜歡的物品越相關(guān)。
(8)
指標(biāo)MRR表示在列表中越早出現(xiàn)的物品其權(quán)重越高。指標(biāo)MRR的高低說(shuō)明了越早出現(xiàn)用戶喜歡的物品的概率大小。MRR越高說(shuō)明推薦列表的前幾項(xiàng)就是用戶感興趣的物品(因?yàn)榱?xí)慣上用戶只關(guān)注列表的前幾項(xiàng)內(nèi)容)。
(9)
指標(biāo)MAP稱(chēng)為平均準(zhǔn)確度,衡量用戶喜歡的物品在列表中出現(xiàn)的頻度。同樣的越早出現(xiàn)在列表中的物品其權(quán)重越高。
(10)
3.3對(duì)比實(shí)驗(yàn)
在這里設(shè)計(jì)三組對(duì)比實(shí)驗(yàn)分別展示三種算法在這三個(gè)評(píng)價(jià)指標(biāo)上的優(yōu)劣程度。
需要說(shuō)明的是與本文算法進(jìn)行對(duì)比的算法是基于用戶的協(xié)同過(guò)濾推薦算法(UserCF)和基于物品的協(xié)同過(guò)濾推薦算法(ItemCF)。
3.3.1第一組對(duì)比實(shí)驗(yàn)
在第一組對(duì)比實(shí)驗(yàn)中我們比較三種算法在指標(biāo)MRR上的優(yōu)劣程度。這里我們隨機(jī)給不同的用戶推薦不同數(shù)量的物品以此來(lái)比較三種算法的情況(用5作為物品列表增加的迭代步長(zhǎng))。
實(shí)驗(yàn)的結(jié)果通過(guò)圖5的柱狀分析統(tǒng)計(jì)圖來(lái)進(jìn)行展示。
通過(guò)上面的柱狀分析圖可以得出這樣的結(jié)論。Pairwise-SVD算法在指標(biāo)MRR上其效果要好于基于物品的協(xié)同過(guò)濾算法和基于用戶的協(xié)同過(guò)濾算法。其中在推薦列表長(zhǎng)度為10的時(shí)候效果最明顯(性能提高約30%左右),而這個(gè)長(zhǎng)度往往是一般推薦系統(tǒng)所選取的給用戶推薦的物品數(shù)量。
3.3.2第二組對(duì)比實(shí)驗(yàn)
在這組實(shí)驗(yàn)中我們關(guān)注三種算法在指標(biāo)Kendall-tau上的性能情況。同上一組實(shí)驗(yàn)一樣我們隨機(jī)選取幾個(gè)用戶進(jìn)行推薦,設(shè)定不同長(zhǎng)度的推薦列表(長(zhǎng)度從5到12)。比較在不同長(zhǎng)度的列表下Kendall-tau值的大小。實(shí)驗(yàn)的結(jié)果如圖6的折線統(tǒng)計(jì)圖所示。
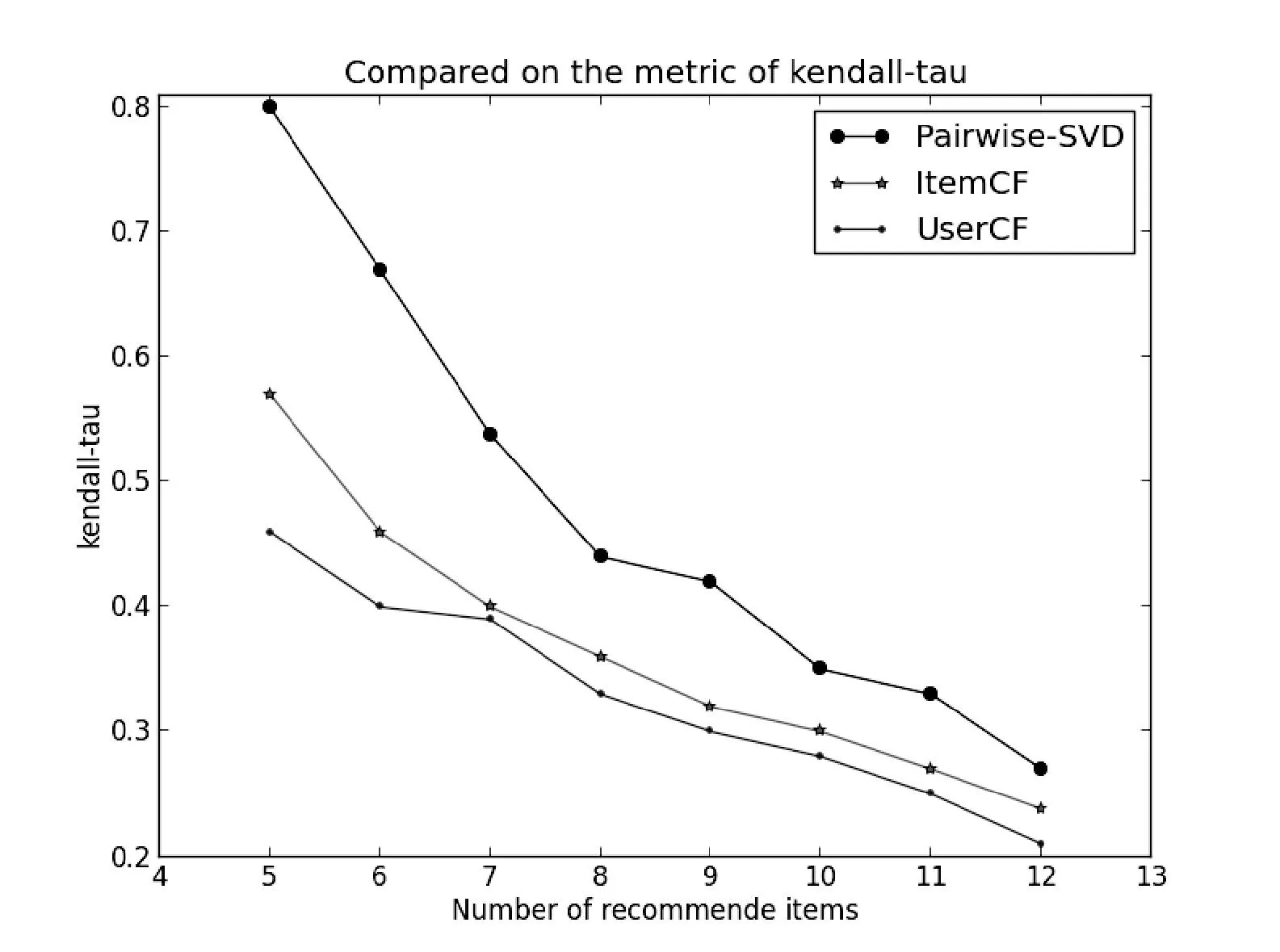
圖6 三種算法在Kendall-tau上的比較
通過(guò)上面的折線圖可以看出Pairwise-SVD算法在指標(biāo)Kendall-tau上要明顯好于另外的兩種算法。這說(shuō)明由Pairwise-SVD算法產(chǎn)生的推薦列表其用戶的興趣與物品之間的相關(guān)度更高。
3.3.3第三組對(duì)比實(shí)驗(yàn)
在這一組實(shí)驗(yàn)當(dāng)中比較三種算法在指標(biāo)MAP上的結(jié)果。并通過(guò)表1來(lái)展示,其中N代表推薦給用戶的物品數(shù)量。
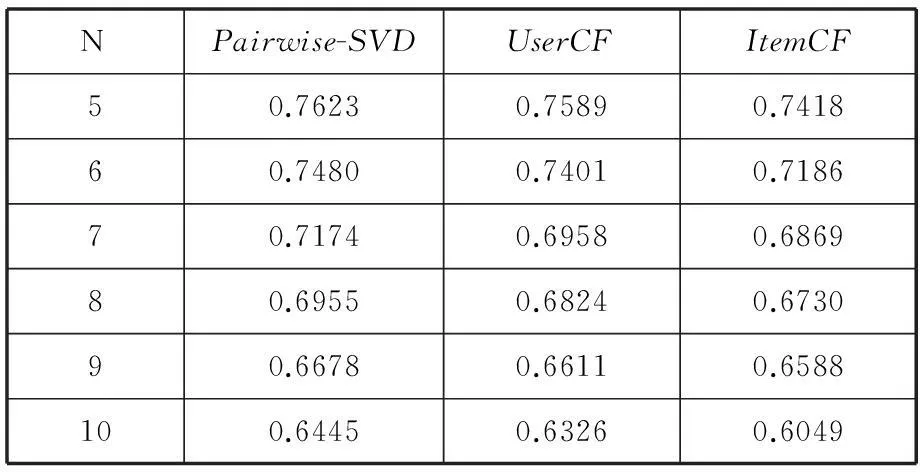
表1 三種算法在MAP上的比較
通過(guò)上面表格中的數(shù)據(jù),可以得出這樣的結(jié)論。即Pairwise-SVD算法在MAP指標(biāo)上相比另外的兩種算法也有一定的優(yōu)勢(shì)。說(shuō)明Pairwise-SVD算法所推薦的物品準(zhǔn)確度與覆蓋效果更好。
4結(jié)語(yǔ)
本文在前人工作的基礎(chǔ)之上提出了基于Pairwise排序?qū)W習(xí)的因子分解推薦算法。把原本只適用于預(yù)測(cè)精度的因子分解推薦算法改造成為適合產(chǎn)生推薦列表的推薦算法。并通過(guò)實(shí)驗(yàn)將該算法與基于內(nèi)存的協(xié)同過(guò)濾推薦推薦算法進(jìn)行對(duì)比。在三個(gè)評(píng)價(jià)指標(biāo)上都取得了比較好的效果。此外加入了Rank-SVM方法把排序問(wèn)題轉(zhuǎn)化為機(jī)器學(xué)習(xí)問(wèn)題使得列表排序更加智能化。本文的工作也為其他的機(jī)器學(xué)習(xí)算法融入推薦算法當(dāng)中做了很好的鋪墊。
在未來(lái)的工作中我們將把其他的分類(lèi)算法比如神經(jīng)網(wǎng)絡(luò)算法等內(nèi)容用于進(jìn)行排序?qū)W習(xí),并在多維特征的情況下進(jìn)行測(cè)試來(lái)驗(yàn)證其效果。未來(lái)將進(jìn)一步深化排序?qū)W習(xí)與推薦系統(tǒng)領(lǐng)域的交叉研究。
參考文獻(xiàn)
[1]YueShi,MarthaLarson,AlanHanjalic.List-wiseLearningtoRankwithMatrixFactorizationforCollaborativeFiltering[C]//Recys’10.Barcelona,Spain:ACM,2010.
[2]SeanMMcNee,JohnRiedl,JosephAKonstan.BeingAccurateisNotEnough:HowAccuracyMetricshavehurtRecommendersystem[C]//Montreal.Quebec,Canada:ACM,2006.
[3]YueShi,AlexandrosKaratzoglou,LinasBaltrunas.CLiMF:LearningtoMaximizeReciprocalRankwithCollaborativeLess-is-MoreFiltering[C]//Dublin,Ireland:Recsys’12,2012.
[4]ShuziNiu,JiafengGuo,YanyanLan,etal.Top-kLearningtoRank:Labeling,RankingandEvaluation[C]//Portland,Oregon,USA:SIGIR’12,2012.
[5] 項(xiàng)亮.推薦系統(tǒng)實(shí)踐[M].北京:人民郵電出版社,2012.
[6] 林原,林鴻飛,蘇綏.一種應(yīng)用奇異值分解的Rankboost排序?qū)W習(xí)方法[C]//中國(guó)山東煙臺(tái),第十屆全國(guó)計(jì)算語(yǔ)言學(xué)學(xué)術(shù)會(huì)議,2009.
[7] 丁偉民.排序?qū)W習(xí)中的RankingSVM算法研究 [J].科技視界,2013(30):84-138.
[8]ChenT,ZhangW,LuQ.SVDFeature:AToolkitforFeature-basedCollabrativeFiltering[C]//Toappearinthe30thInternationalConferenceonMachineLearningResearch,2012:3585-3588.
FACTORISATION RECOMMENDATION ALGORITHM BASED ONPAIRWISERANKINGLEARNING
Zhou JunyuDai YuemingWu Dinghui
(School of Internet of Things,Jiangnan University,Wuxi 214122,Jiangsu,China)
AbstractMemory-based collaborative filtering recommendation algorithm has the problem of poor recommendation list ranking effect, in light of this, we presented a new kind of factorisation recommendation algorithm which is based on Pairwise ranking learning, namely the Pairwise-SVD recommendation algorithm. The new algorithm uses the predictive result of factorisation as the input of ranking learning algorithm, in this way, it converts the ranking problem into a classification problem and then uses the ranking learning theory to rank and generates a recommendation list. Experimental results showed that, compared with the memory-based collaborative filtering recommendation algorithm, the Pairwise-SVD recommendation algorithm had better ranking effect. What’s more, it almost doubled the index of Kendall-tau, and improved about 30% in index of MRR, and reached a small improvement in the index of MAP as well.
KeywordsPairwiseFactorisationCollaborative filteringClassificationRanking learning
收稿日期:2015-01-18。國(guó)家高技術(shù)研究發(fā)展計(jì)劃項(xiàng)目(2013AA 040405)。周俊宇,碩士生,主研領(lǐng)域:數(shù)據(jù)挖掘與推薦系統(tǒng)。戴月明,副教授。吳定會(huì),副教授。
中圖分類(lèi)號(hào)TP3
文獻(xiàn)標(biāo)識(shí)碼A
DOI:10.3969/j.issn.1000-386x.2016.06.061

