輸入非均勻采樣廣義輸出誤差模型的遞推貝葉斯參數(shù)辨識(shí)算法
景 紹 學(xué)
(淮安信息職業(yè)技術(shù)學(xué)院電氣工程系 江蘇 淮安 223003)(江蘇大學(xué)電氣信息工程學(xué)院 江蘇 鎮(zhèn)江 212013)
?
輸入非均勻采樣廣義輸出誤差模型的遞推貝葉斯參數(shù)辨識(shí)算法
景 紹 學(xué)
(淮安信息職業(yè)技術(shù)學(xué)院電氣工程系江蘇 淮安 223003)(江蘇大學(xué)電氣信息工程學(xué)院江蘇 鎮(zhèn)江 212013)
摘要針對(duì)傳統(tǒng)最小二乘算法在辨識(shí)過程中沒有考慮噪聲的協(xié)方差和參數(shù)的先驗(yàn)概率密度的問題,提出一種遞推貝葉斯算法。該算法以最大化參數(shù)的后驗(yàn)概率密度函數(shù)為準(zhǔn)則進(jìn)行參數(shù)估計(jì)。實(shí)驗(yàn)結(jié)果證明所提算法可以獲得更高精度的參數(shù)估計(jì)值。收斂性分析表明,該算法給出的參數(shù)估計(jì)值收斂于參數(shù)真值。該算法綜合考慮了噪聲方差、數(shù)據(jù)的先驗(yàn)概率分布和參數(shù)的先驗(yàn)概率分布,可以獲得比最小二乘法更高的精度的估計(jì)值。
關(guān)鍵詞輸入非均勻采樣系統(tǒng)廣義輸出誤差模型遞推貝葉斯算法參數(shù)估計(jì)
0引言
在工業(yè)生產(chǎn)中存在著這樣一類系統(tǒng),它們的輸入采樣和(或)輸出刷新呈現(xiàn)出不等時(shí)間間隔的非均勻的特點(diǎn),這類系統(tǒng)被稱為非均勻采樣系統(tǒng)[1,2]。這類系統(tǒng)有的是由于硬件設(shè)備的限制、經(jīng)濟(jì)條件的制約或環(huán)境因素的影響等原因造成的被動(dòng)非均勻采樣系統(tǒng),如產(chǎn)品組分和濃度的檢測[3,4]、熔融指數(shù)的人工采樣[5,6]和Kappa值的測量[7,8]等。還有的是為了在同樣采樣點(diǎn)數(shù)的情況下獲得更多的有用信號(hào)而根據(jù)信號(hào)幅值變化情況主動(dòng)調(diào)整采樣間隔的主動(dòng)非均勻采樣系統(tǒng)[9]。近年來,非均勻采樣系統(tǒng)的研究受到了國內(nèi)外專家和學(xué)者的普遍關(guān)注,特別是作為狀態(tài)估計(jì)和控制理論基礎(chǔ)的系統(tǒng)辨識(shí)領(lǐng)域[10-18]。
在白噪聲的前提下,傳統(tǒng)算法,如最小二乘算法等,都能給出非均勻采樣系統(tǒng)的參數(shù)無偏估計(jì)。而在工業(yè)實(shí)踐中的擾動(dòng)都是有色噪聲,傳統(tǒng)的最小二乘等算法不能滿足無偏估計(jì)的要求[19]。為了獲得參數(shù)的無偏估計(jì),研究人員提出了一系列的算法。例如,基于濾波的算法[20]、最大似然算法[21,22]、基于輔助模型的算法[23]等。基于濾波的算法首先采樣一個(gè)動(dòng)態(tài)的濾波器來白化有色噪聲,然后使用傳統(tǒng)算法,如最小二乘算法等,獲得無偏估計(jì)。但是當(dāng)工業(yè)過程輸出信號(hào)噪信比較大或者參數(shù)較多時(shí)這類算法會(huì)出現(xiàn)估計(jì)偏差[24]。并且最大似然類算法給出的估計(jì)值都是漸近無偏的,也就是說最大似然算法并不能保證給出的所有估計(jì)都是無偏的。此外,最大似然算法的計(jì)算量比較大,也在一定程度上限制了其應(yīng)用[24]。基于輔助模型的算法,如基于輔助模型的遞推最小二乘算法(AM-RLS)和基于輔助模型的隨機(jī)梯度(AM-SG)等,可以同時(shí)對(duì)系統(tǒng)模型和噪聲模型的無偏估計(jì),是一類比較有應(yīng)用前景的算法。但在辨識(shí)過程中,AM-RLS和AM-SG都沒有把系統(tǒng)噪聲的方差考慮進(jìn)辨識(shí)算法以提高算法的辨識(shí)精度,所以本文的基本思路是考慮結(jié)合噪聲的方差,基于輔助模型的思想和遞推最小二乘的形式提出一種遞推貝葉斯RB(recursiveBayesian)辨識(shí)算法。并用輸入非均勻采樣廣義輸出誤差模型NUSIDGOE(non-uniformlysampledinputdataforgeneralizedoutputerrormodel)驗(yàn)證了算法的有效性。
1問題描述
考慮如圖1所示的輸入非均勻更新和輸出定期采樣的NUSIDGOE模型。圖中,包括零階保持器Hτ、線性時(shí)不變過程Pc和采樣器ST三個(gè)部分。其中,u(t)和x(t)分別是輸入信號(hào)和無噪輸出信號(hào);y(t)為有噪輸出;w(t)是有色噪聲;y(kT+T)是采樣時(shí)刻t=kT+T時(shí)刻的輸出采樣值,其中T為輸出采樣周期,也稱框架周期。

圖1 輸入非均勻采樣廣義輸出誤差模型框圖
假定輸入非均勻采樣時(shí)間間隔為{τ1,τ2,…,τr},它們滿足如下的條件:T=τ1+τ2+…+τr。定義t0=0,ti=ti-1+τi,其中i=1,2,…,r,那么輸入u(t)可以寫為:
(1)
其中k=0,1,2,…。
如圖1所示,若Pc和w(t)采用文獻(xiàn)[20]的形式,則NUSIDGOE模型的連續(xù)輸出y(t)可以表示為:
y(t)=x(t)+w(t)
(2)
其中:
(3)
(4)
A(z-1) = 1 +a1z-1+a2z-2+ … +anaz-na,B1(z-1) =b10+b11z-1+b12z-2+ … +b1n bz-nb,Bi(z-1) =bi1z-1+bi2z-2+ … +bin bz-nb
(5)
C(z-1)=1+c1z-1+c2z-2+…+cncz-nc,D(z-1)=1+d1z-1+d2z-2+…+dndz-nd
(6)
定義參數(shù)向量如下:
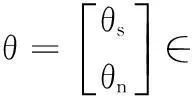
(7)
其中:
θs=[a1,…,ana,b10,…,b1nb,b21,…,b2nb,…,br1,…,brnb]T∈ns
(8)
θn=[c1,c2,…,cnc,d1,d2,…,dnd]T∈nn
(9)
ns=na+rnb+1,nn=nc+nd,n=ns+nn;下標(biāo)s和n分別表示過程模型和噪聲模型。
類似地,分別定義信息向量φ如下:
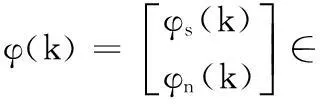
(10)
φs(k)= [-x(kT-T),…,-x(kT-naT),u(kT),…,
u(kT-nbT),u(kT-T+t1),…,u(kT-nbT+t1),
…,u(kT-T+tr-1),…,u(kT-nbT+tr-1)]T∈ns
(11)
φn(k)=[-w(kT-T),-w(kT-2T),…,-w(kT-ncT),
v(kT-T),v(kT-2T),…,v(kT-ndT)]T∈nn
(12)
對(duì)于t=kT時(shí)刻,等式可以改寫成:
y(k)=x(k)+w(k)=φT(k)θ(k)+v(k)
(13)
其中:
(14)
(15)
假定系統(tǒng)的模型結(jié)構(gòu)是已知的,即(na,nb,nc,nd)和輸入采樣次數(shù)r均是已知的,那么算法的目的就是如何利用觀測數(shù)據(jù)D(k)估計(jì)參數(shù)向量θ。
2遞推貝葉斯參數(shù)辨識(shí)算法
貝葉斯方法的主要觀點(diǎn)就是把待估計(jì)參數(shù)作為一個(gè)隨機(jī)變量,通過觀測與該變量相關(guān)的其他隨機(jī)變量來推測該變量的值[25]。在提出的算法中,以最大化后驗(yàn)概率密度作為估計(jì)準(zhǔn)則,即:
(16)
根據(jù)貝葉斯公式,參數(shù)的后驗(yàn)概率密度函數(shù)表示為:
(17)
其中p(y(k)|θ,D(k-1))為在給定參數(shù)θ和數(shù)據(jù)條件下輸出y(k)的先驗(yàn)概率密度。
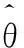
(18)

(19)
于是參數(shù)的后驗(yàn)密度函數(shù)p(θ|Dk)的表達(dá)式為:
(20)
(21)
其中:
(22)
(23)
這樣就得到了遞推貝葉斯(RB)算法的簡潔形式:式(22)和式(23)。為了避免計(jì)算P(k)的逆矩陣以減小算法的計(jì)算量,對(duì)式(23)運(yùn)用矩陣求逆反演公式,得到:
(24)
(25)
(26)
P(k)=[I-L(k)φT(k)]P(k-1)
(27)


(28)
其中:

u(kT-nbT),u(kT-T+t1),…,u(kT-nbT+t1),
…,u(kT-T+tr-1),…,u(kT-nbT+tr-1)]T∈ns
(29)
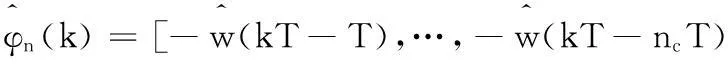
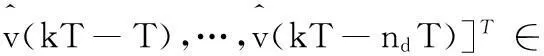
(30)
(31)

(32)
(33)
噪聲方差可以用下式進(jìn)行估計(jì):
(34)
于是,RB算法可以整理如下:
(35)
(36)
(37)
RB算法的計(jì)算步驟如下:
Step1收集輸入輸出數(shù)據(jù)u(kT+ti)和y(k),i=0,1,2,…,r,k=1,2,…。
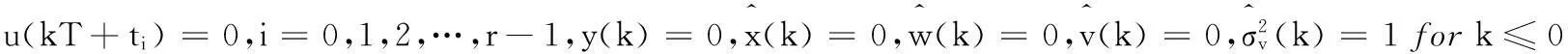

P(0)=p0In,θ(0)=1n/p0,p0=106
其中1n為元素全為1的n維列向量。
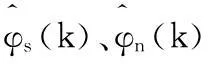
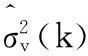


Step8令k=k+1,轉(zhuǎn)step4。
3收斂性分析
定理1對(duì)于系統(tǒng)式(13)和RB算法式(22)、式(23),假設(shè){v(t),Ft}是定義在概率空間{Ω,F,P}上的鞅差向量序列,其中{Ft}是截至?xí)r刻t之前所有觀測數(shù)據(jù)生成的σ代數(shù)序列[26];如果噪聲序列{v(t)}滿足如下假設(shè):

(38)
并且存在正常數(shù)c1,c2和t0使得下面的持續(xù)激勵(lì)條件成立[27]:

(39)
那么算法給出的參數(shù)估計(jì)值收斂于真值,即:
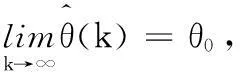
(40)
其中θ0為參數(shù)真值。
證明在式兩邊同時(shí)減去θ0并用φT(k)θ0+v(k)代替y(k),得到:

(41)
其中:
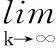
在式(23)兩邊同乘以P(k),則Q(k)可以寫成:
(42)
令λ為矩陣Q(k)的一個(gè)特征值,p為其對(duì)應(yīng)的特征向量,那么下式成立:
Q(k)p=λp
(43)
考慮到式(42)、式(43)可以寫成:
P(k)P-1(k-1)p=λp
(44)
在式(44)的兩邊同乘以P-1(k),考慮到式(23),并整理得:
(45)
在式(45)兩邊同乘以pT并整理得:
(46)
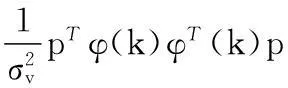
4仿真實(shí)例
考慮如下的NUSIDGOE模型:
其中:
A(z)=1-1.4780z-1+0.9324z-2
B1(z)=0.1519+0.04206z-1
B2(z)=0.0779+0.1824z-1
C(z)=1-0.6z-1
D(z)=1+0.33z-1
r=2,τ1=2s,τ2=5s,t1=τ1=2s,t2=τ1+τ2=7s

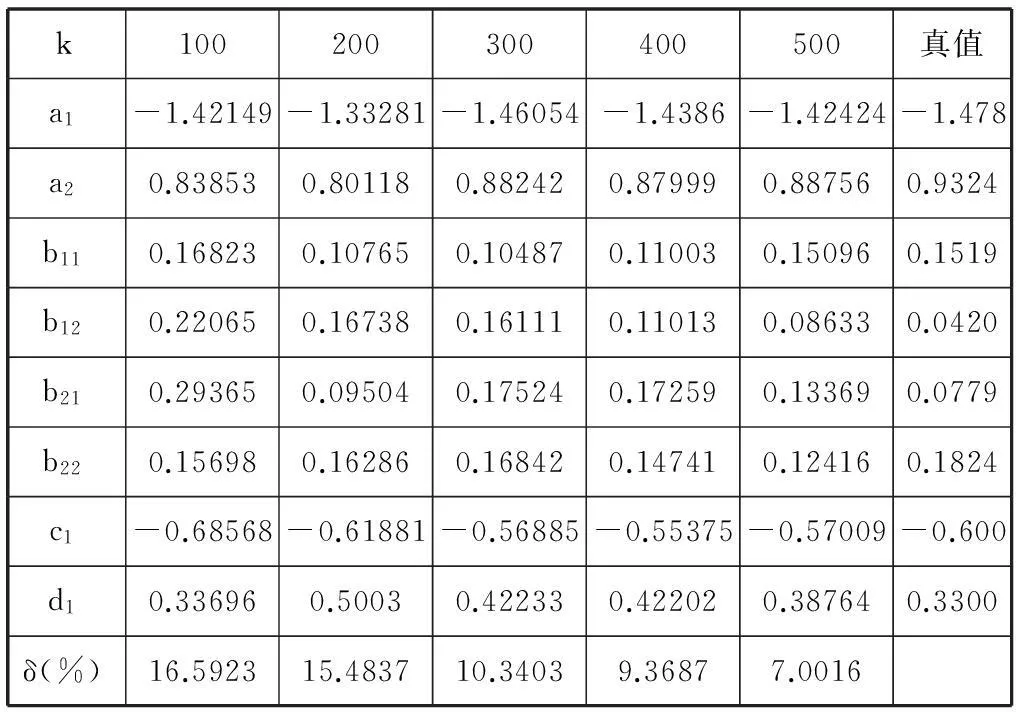
表1 RB算法參數(shù)估計(jì)值和估計(jì)誤差隨數(shù)據(jù)長度k變化情況
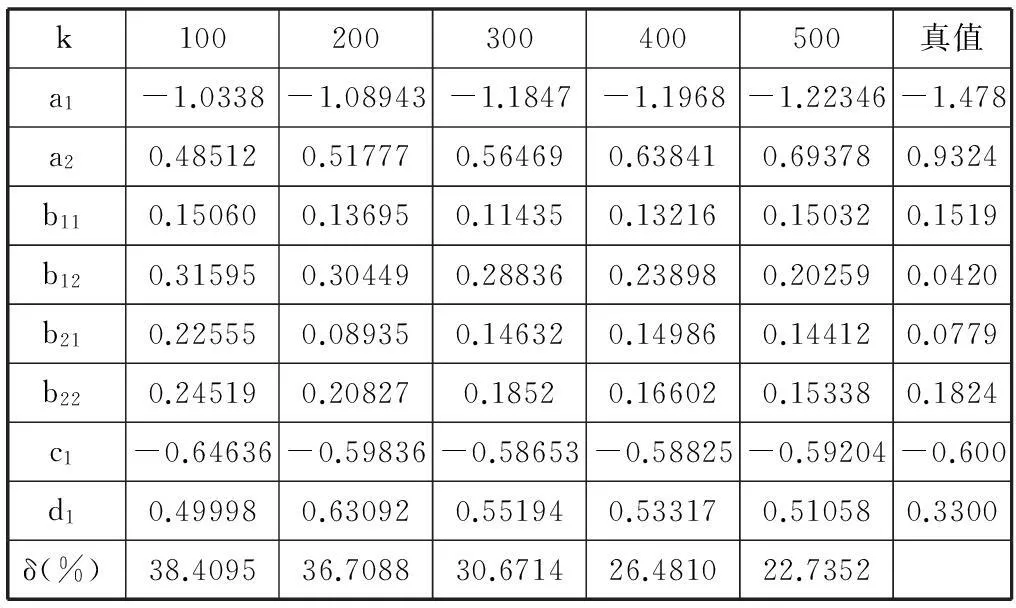
表2 AM-RGELS算法參數(shù)估計(jì)值和估計(jì)誤差隨數(shù)據(jù)長度k變化情況
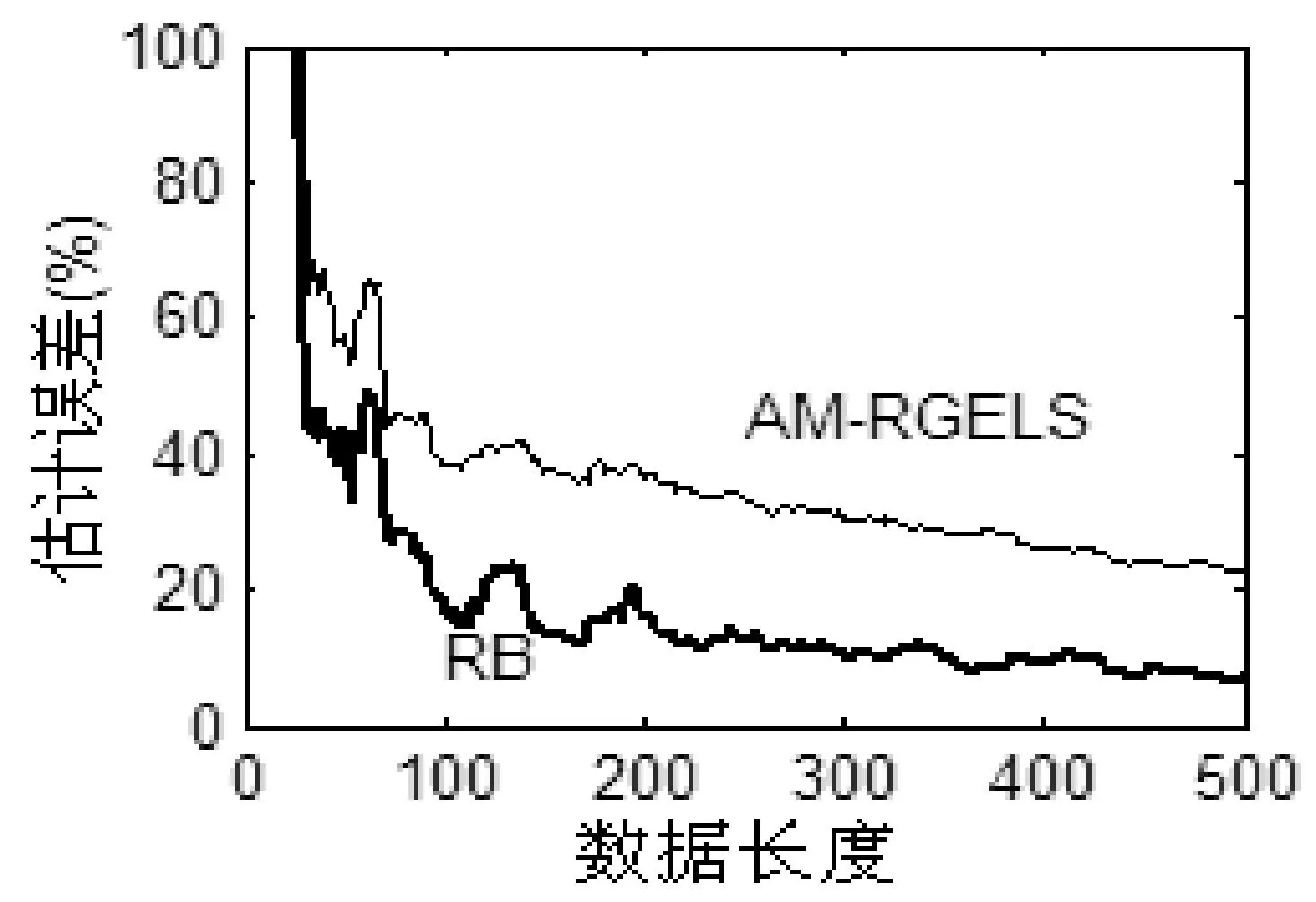
圖2 RB和AM-RGELS算法參數(shù)估計(jì)誤差隨數(shù)據(jù)長度變化情況圖
根據(jù)表1、表2的數(shù)據(jù)和圖2的仿真結(jié)果可以看出:
(1) 數(shù)據(jù)長度增加時(shí),兩種算法的估計(jì)誤差都在變小;
(2) 對(duì)同樣的數(shù)據(jù)長度,RB算法比AM-RGELS算法的估計(jì)精度高;
(3) 在相同噪聲水平下,RB算法比AM-RGELS算法的收斂速度要快。
5結(jié)語
本文針對(duì)輸入非均勻采樣廣義輸出誤差模型提出了一種遞推貝葉斯參數(shù)估計(jì)算法。它以通過最大化參數(shù)的條件后驗(yàn)概率密度函數(shù)作為估計(jì)準(zhǔn)則,由于不僅考慮了參數(shù)的先驗(yàn)概率密度而且還考慮了數(shù)據(jù)的先驗(yàn)概率密度。因此該算法與單純考慮數(shù)據(jù)的概率密度的極大似然類參數(shù)估計(jì)方法相比,精度更高。同時(shí),該算法的辨識(shí)精度也會(huì)比傳統(tǒng)最小二乘算法略高,因?yàn)樗诒孀R(shí)過程中考慮了噪聲的方差。綜上所述,該算法把給定數(shù)據(jù)集下最可能出現(xiàn)的參數(shù)值作為參數(shù)的估計(jì)值。收斂性分析表明,所提算法的參數(shù)估計(jì)值能收斂到真值,仿真結(jié)果表明了算法的有效性和較高的估計(jì)精度。
參考文獻(xiàn)
[1]AlbertosP,CrespoA.Real-timecontrolofnon-uniformlysampledsystems[J].ControlEngineeringPractice,1999,7(4):445-458.
[2]CuencaA,SaltJ.RSTcontrollerdesignforanon-uniformmulti-ratecontrolsystem[J].JournalofProcessControl,2012,22(10):1865-1877.
[3]LiW,HanZ,ShanSL.SubspaceidentificationforFDIinsystemswithnon-uniformlysampledmultiratedata[J].Automatica,2006,42(4):619-627.
[4]DingF,LiuG,LiuXP.Partiallycoupledstochasticgradientidentificationmethodsfornon-uniformlysampledsystems[J].IEEETransactionsonAutomaticControl,2010,55(8):1976-1981.
[5]FortunaL,GrazianiS,XibilliaM.Softsensorsforproductqualitymonitoringindebutanizerdistillationcolumns[J].ControlEngineeringPractice,2005,13(4):499-508.
[6]GjerkesH,MalensekJ,SitarA,etal.Productidentificationinindustrialbatchfermentationusingavariableforgettingfactor[J].ControlEngineeringPractice,2011,19(10):1208-1215.
[7]OgawaM,OhshimaM,MorinagaK,etal.Dualityinferentialcontrolofanindustrialhighdensitypolyethyleneprocess[J].JournalofProcessControl,1999,9(1):51-59.
[8]SharminR,SundararajU,ShanS,etal.Inferentialsensorsforestimationofpolymerqualityparameters:IndustrialapplicationofaPLS-basedsoftsensorforaLDPEplant[J].ChemicalEngineeringScience,2006,61(19):6372-6384.
[9] 汪安民.基于非均勻采樣的信號(hào)頻率檢測方法及其實(shí)現(xiàn)[D].武漢:華中科技大學(xué),2004.
[10] 丁鋒,陳通文,蕭德云.非均勻周期采樣多率系統(tǒng)的一種辨識(shí)方法[J].電子學(xué)報(bào),2004,32(9):1414-1420.
[11]MizumotoI,ChenT,OhdairaS,etal.AdaptiveoutputfeedbackcontrolofgeneralMIMOsystemsusingmultiratesamplinganditsapplicationtoacart-cranesystem[J].Automatica,2007,43(12):2077-2085.
[12]ChenF,GilsonM,AgueroJC,etal.Closed-loopidentificationofcontinuous-timesystemsfromnon-uniformlysampleddata[C]//ControlConference(ECC),2014European.Strasbourg:IEEE,2014.
[13]JohanssonR,CesconM,StahlF.Continuous-timemodelidentificationusingnon-uniformlysampleddata[C]//AFRICON,2013.Mauritius:IEEE,2013.
[14]DingJ,LinJ.Modifiedsubspaceidentificationforperiodicallynon-uniformlysampledsystemsbyusingtheliftingtechnique[J].Circuits,Systems,andSignalProcessing,2014,33(5):1439-1449.
[15]WangH,LiuT.Recursivestate-spacemodelidentificationofnon-uniformlysampledsystemsusingsingularvaluedecomposition[J].ChineseJournalofChemicalEngineering,2014,89(1):1-6.
[16]DingF.Hierarchicalmulti-innovationstochasticgradientalgorithmforHammersteinnonlinearsystemmodeling[J].AppliedMathematicalModelling,2013,37(4):1694-1704.
[17]ChenF,GarnierH,GilsonM.RefinedInstrumentalVariableIdentificationofContinuous-timeOEandBJModelsfromIrregularlySampledData[C]//11thIFACInternationalWorkshoponAdaptationandLearninginControlandSignalProcessing.Caen:IFAC,2013.
[18]DingF,ChenT.Hierarchicalidentificationofliftedstate-spacemodelsforgeneraldual-ratesystems[J].IEEETransactionsonCircuitsandSystemsI:fundamentaltheoryandapplications.2005,52(6):1179-1187.
[19] 崔桂梅,關(guān)英輝,張勇.一類有色噪聲干擾系統(tǒng)的有辨識(shí)研究[J].科學(xué)技術(shù)與工程,2010,10(18):4358-4362.
[20]XieL,YangHZ,DingF.Recursiveleastsquaresparameterestimationfornon-uniformlysampledsystemsbasedonthedatafiltering[J].MathematicalandComputerModeling,2011,54(1):315-324.
[21]LiJH,DingF.MaximumlikelihoodstochasticgradientestimationforHammersteinsystemswithcolorednoisebasedonthekeytermseparationtechnique[J].Computers&MathematicswithApplications,2011,62(11):4170-4177.
[22]LiJH,DingF,YangGW.Maximumlikelihoodleastsquaresidentificationmethodforinputnonlinearfiniteimpulseresponsemovingaveragesystems[J].MathematicalandComputerModeling,2012,55(3-4):442-450.
[23] 丁鋒.系統(tǒng)辨識(shí)(4):輔助模型辨識(shí)思想與方法[J].南京信息工程大學(xué)學(xué)報(bào):自然科學(xué)版,2011,3(4):289-318.
[24] 方崇智,蕭德云.過程辨識(shí)[M].北京:清華大學(xué)出版社,1988.
[25]PeterkaV.BayesianApproachtoSystemIdentification:TrendsandProgressinSystemIdentification[M].NewYork:PergamonPress,1981.
[26]GoodwinG,SinK.AdaptiveFilteringPredictionandControl[M].NewYork:Prentice-Hall,1984.
[27]DingF,ChenHB,LiM.Multi-innovationleastsquaresidentificationmethodsbasedontheauxiliarymodelforMISOsystems[J].InternationalJournalofAppliedMathematicsandComputerScience,2007,187(2):658-668.
RECURSIVE BAYESIAN PARAMETER IDENTIFICATION ALGORITHM FOR GENERALOUTPUTERRORMODELSWITHNON-UNIFORMLYSAMPLEDINPUTDADA
Jing Shaoxue
(Department of Electrical Engineering,Huaian College of Information and Technology,Huaian 223003,Jiangsu,China)(School of Electrical and Information Engineering,Jiangsu University,Zhenjiang 212013,Jiangsu,China)
AbstractIn light of that traditional least squares method does not take into account the covariance of noise and the priori probability density of parameters in the process of identification, we proposed a recursive Bayesian parameter identification algorithm. The algorithm uses the posterior probability density function of maximised parameters as the criterion to estimate parameters. Experimental result proved that the proposed algorithm could acquire the estimates of parameters in higher accuracy. Convergence analysis indicated that the estimates of parameters provide by the proposed algorithm converged to their true values. The algorithm comprehensively considers the noise variance and the priori probability distributions of data and parameters, it is able to obtain the estimates with higher accuracy than the least-squares.
KeywordsNon-uniformly sampled input data systemsGeneral output error modelRecursive Bayesian algorithmParameter estimation
收稿日期:2014-12-08。江蘇省研究生培養(yǎng)創(chuàng)新工程項(xiàng)目(CXLX12_0648)。景紹學(xué),講師,主研領(lǐng)域:過程控制,系統(tǒng)辨識(shí)。
中圖分類號(hào)TP273
文獻(xiàn)標(biāo)識(shí)碼A
DOI:10.3969/j.issn.1000-386x.2016.06.078

