機翼折疊運動的瞬態動力學響應分析

倪迎鴿, 侯赤, 萬小朋, 趙美英

(西北工業大學 航空學院, 陜西 西安　710072)

?

機翼折疊運動的瞬態動力學響應分析

倪迎鴿, 侯赤, 萬小朋, 趙美英

(西北工業大學 航空學院, 陜西 西安710072)

摘要：結合多體動力學中的浮動坐標系法和結構動力學中的模態綜合法,建立了機翼折疊運動的動力學控制方程,預測了機翼折疊運動中的瞬態動力學特性。將有理函數近似導出的折疊運動中的非定常氣動力引入到動力學控制方程中,獲得了機翼折疊運動中在時變氣動力作用下的瞬態動力學響應。結果表明:機翼折疊過程越緩慢,得到的瞬態響應越平穩;機翼柔性對折疊變形過程中的瞬態響應影響較大;在一定的來流速度范圍內,來流速度越大,穩態時翼尖位移響應的振蕩越小,越有助于機翼的折疊變形。

關鍵詞：折疊機翼;瞬態動力學響應;有理函數近似;浮動坐標系法;模態綜合法

變體飛機通過機翼折疊可實現機翼面積200%的變化[1]。這種大幅度變形必然會引起機翼的氣動力以及結構動力學特性的變化。因此需要對變體飛機機翼在折疊變形過程中的動力學特性進行研究。Scarlett等[2]和Reich等[3]結合有限元方法、多體動力學、氣動力模型,建立了折疊機翼柔性多體動力學模型。韓景龍課題組[4]通過對偶極子網格法的有理近似,并結合MSC. NASTRAN與ADAMS,建立了多體動力學的瞬態響應。此時使用的商業軟件不便于結構模型與氣動力模型的耦合。Selitrennik等[5]通過引入時變的坐標變換矩陣、虛質量子結構綜合方法以及CFD計算結果,形成了狀態空間下的氣動彈性模型,但是該模型中CFD的計算量較大。Zhao等[6]建立了機翼在折疊變形的動力學方程,預測了機翼在不同變形速度下的動力學響應,但是該模型沒有考慮氣動力的作用,因此無法預測氣動力對于機翼在折疊變形過程中動力學響應的影響。

本文采用多體動力學中的浮動坐標系法,結構動力學中的模態綜合法,引入有理函數近似導出機翼折疊變形時非定常氣動力,建立了一組微分代數方程來模擬機翼的折疊運動,通過約束違約穩定法[7]獲得了機翼折疊運動的動力學響應。該控制方程適用類似的多段機翼結構,并且可以改變約束方程,獲得不同變形方式下的動力學響應。

1機翼折疊變形過程中的動力學控制方程

機翼的幾何模型如圖1 所示。該模型由機身, 內翼和外翼3個子結構組成,分別記為子結構A、B、C。機翼折疊運動的瞬態響應,可以看作是剛體運動和彈性變形的疊加。而浮動坐標系法就是將柔性體的運動分解為剛性運動和相對浮動坐標系的彈性變形[8]。另外,對于機翼這樣的復雜結構,采用有限元離散方法所得的自由度龐大,不利于動力學方程的求解。而子結構模態綜合法是對復雜結構進行動力學建模的有效手段。因此,多體動力學中浮動坐標系法和結構動力學中的模態綜合法的結合是解決該問題比較好的方法[6]。如圖1所示,oxyz為慣性坐標系,用于描述系統的運動,oAxAyAzA、oBxByBzB、oCxCyCzC分別為浮動坐標系,用于描述柔性體的彈性變形。θA、θB、θC分別為子結構A、B、C的折疊角。

圖1　機翼的幾何示意圖以及坐標系

結合浮動坐標系法[8]以及模態綜合法[9],機翼的子結構的動力學方程為

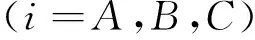
(1)

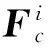
(2)

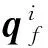
1.1機翼結構的模態綜合中的模態集選取

對于機翼結構,需要采用有限元方法對結構進行離散,提取模態信息,創建廣義質量矩陣中柔性體彈性變形的慣性項,再根據柔性多體動力學理論建立動力學控制方程。子結構模態綜合將復雜結構劃分為若干子結構,建立子結構的模態集及模態坐標,利用界面的協調條件將各個子結構組裝得到整體結構動力學方程。此時所選取的模態集直接決定著柔性體變形量的準確性。因此,這里詳細給出模態集的確定。采用有限元離散化形成的無阻尼動力學方程為

(3)

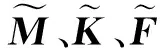
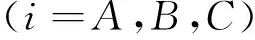
(4)

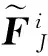
(5)

式中,φn為固定界面的主模態矩陣,φc為約束模態矩陣。此時模態矩陣包含子結構的6個剛體模態,不能直接應用于機翼折疊變形的瞬態響應分析。因此,需要進行矩陣變換。為了求得變換矩陣,對下列公式進行特征值求解

(6)

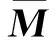
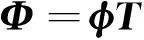
(7)

此時剛體模態就會顯式地表達出來,剔除這些剛體模態,便可以建立機翼的結構動力學方程。在工程中,阻尼矩陣可以通過模態阻尼比給出。此時,引入阻尼矩陣,機翼子結構結構動力學方程為

(8)

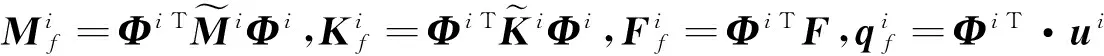
1.2機翼折疊變形過程中的時變氣動載荷

采用偶極子法可以獲得頻域下的非定常氣動力,通過有理近似可以導出任意運動情況下的非定常氣動力。因此給時域非定常氣動力的模擬提供了思路。作為機翼折疊變形中的氣動載荷初步研究,本文采用偶極子網格法獲得了機翼的氣動力。根據虛功原理,可以得到作用在結構網格節點的等效力

(9)

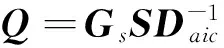
1.3機翼折疊變形的動力學控制方程

引入作用在結構網格節點的等效力

(10)

此時Q為頻域氣動力。為了進行機翼折疊變形時的瞬態響應分析,這里采用最小狀態法進行頻域氣動力的有理函數近似獲得時域內的氣動力。此時有

(11)

式中,A0、A1、A2、Ds和Es,均為最小狀態法近似中的未知矩陣,可以通過最小二乘法求得,Rs為氣動力滯后矩陣。qa為氣動力狀態變量。

對于機翼的折疊變形運動,存在著運動約束和驅動約束,可以表達成如下形式

(12)

式中

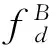
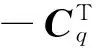
(13)

式中,M=blockdiag(MA,MB,MC),D=blockdiag(DA,DB,DC),K=blockdiag(KA,KB,KC)。可以看出該動力學控制方程是微分代數方程,對于該方程可以采用約束違約穩定法來求解[8]。將約束方程對時間進行2次求導,可以得到約束加速度方程,此時可以得到

(14)

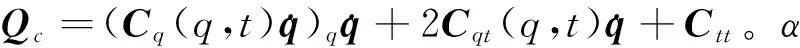
2機翼折疊變形中的瞬態動力學響應分析

為了預測機翼折疊變形的動力學響應,令折疊角θB的變化符合以下規律

(15)

式中,120°代表機翼折疊變形結束時,子結構B所要達到的角度。Ts代表變形結束時所需要的時間。

本文將各個子結構簡化為等厚度的鋁板,在MSC.NASTRAN中被離散成四節點的CQUAD4單元,其單元屬性為PSHELL,這樣單元的每個節點有6個自由度,即3個平動自由度ux、uy、uz,以及3個轉動自由度θx、θy、θz。機翼的有限元模型如圖2所示。通過DMAP語言來獲得子結構的質量矩陣和剛度矩陣,對于每個子結構均保留6階模態,每階所對應的模態阻尼比為0.01。因此最終得到機翼折疊變形的動力學控制方程,即公式(14)有46個方程,采用約束違約穩定法解進行求解,本文中取α=5,β=10,整個程序的編制均在MATLAB中完成。

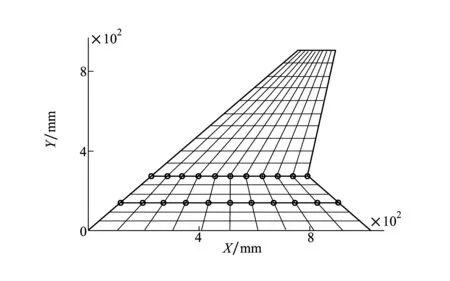
圖2　機翼的有限元模型

2.1柔性機翼在重力作用下瞬態響應

首先,不考慮氣動力的作用。即在公式(14)中忽略與氣動力有關的項。翼尖法向位移響應如圖3所示。

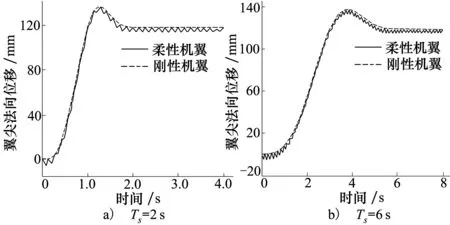
圖3　翼尖法向位移響應

當Ts=2 s,Ts=6 s時,分別在1.27 s、3.81 s附近,θB=90°,此時子結構B與子結構A與C垂直,翼尖法向位移達到最大值。明顯地,柔性對翼尖法向位移響應有較大影響。在整個變形中,翼尖的位移衰減收斂,并且變形結束時,位移穩定值要比剛性機翼時的位移穩定值要小。由于在公式(14)中引入了結構阻尼,位移響應呈收斂的趨勢。Ts越大,意味著變形越緩慢,翼尖的法向位移變化也較緩慢。

對于剛性機翼,作用在子結構B上合力在機翼折疊變形開始和結束時的值均等于子結構B的重力,即4.89 N。而作用在子結構B上的合力矩,在變形運動開始時大約為341.36 Nmm,在變形結束時保持在-157.18 Nmm。初始值和穩定值均等于子結構B的重力產生的力矩。作用在子結構C上的合力,初值和穩定值基本為子結構C的重力,即11.564 N。作用在子結構C上的力矩,其初值和穩定值基本一樣,均為2 885 Nmm。這是因為機翼在折疊變形的過程中,子結構C始終保持水平,所以子結構C的重心相對于其浮動坐標系沒有很大的變化。在變形的過程中,無論是作用在子結構B上的合力、合力矩,還是作用在子結構C的力、力矩,均發生變化。

柔性對作用在子結構B上的合力、合力矩,以及作用在子結構C上的力、力矩有較大的影響。與剛性相比,作用在柔性子結構B上的合力有較大振蕩,已經改變了在剛性狀態下的變化趨勢,但是隨著時間的增加,合力呈收斂的趨勢。對于合力矩而言,也有一定的震蕩。作用在柔性子結構C上的合力、合力矩有較大的振蕩,均呈衰減收斂的趨勢。重力是一種體力,柔性體重力產生的廣義力與彈性變形有關。所以在折疊變形時彈性變形發生變化,另外,彈性力與阻尼力也會對合力和合力矩產生一定的影響。

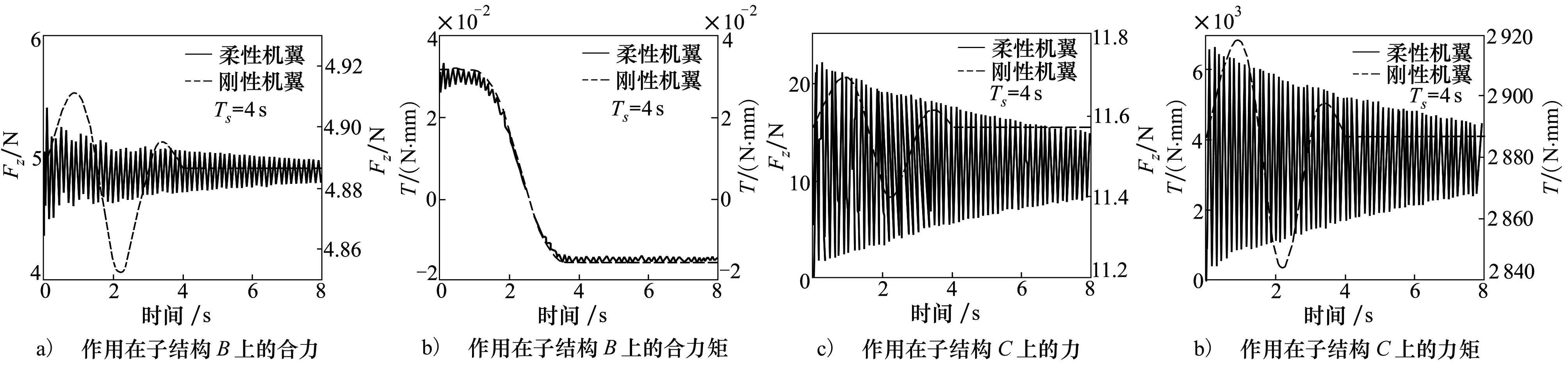
圖4　柔性機翼在重力作用下的力學響應

2.2柔性機翼在重力和氣動力作用下瞬態響應

其次,考慮在重力和氣動力同時作用下柔性機翼的瞬態響應,在公式(14)中,ρ=1.226kg/m3,M∞=0.0,分別計算了不同來流速度下的瞬態響應如圖5和圖6所示。

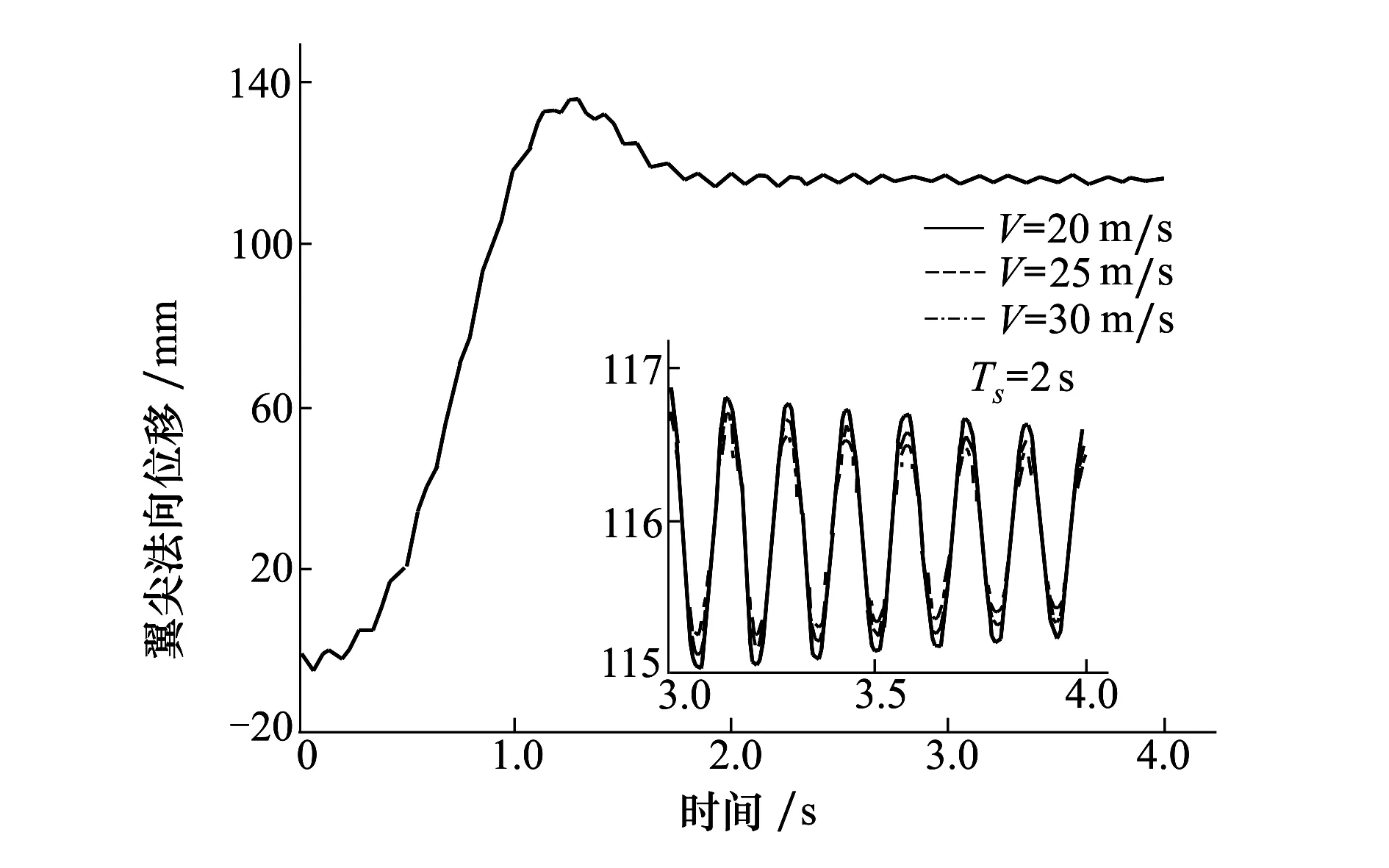
圖5　不同來流速度下翼尖法向位移響應

不同來流速度下翼尖法向位移響應如圖5所示。當Ts=2s時,在1.27s附近,θB=90°,翼尖法向位移達到最大值。與柔性機翼的位移響應有些類似,在不同的來流速度下翼尖的法向位移有一定的振蕩。但從局部的放大圖中可以看出,隨著來流速度的增加,折疊變形結束時的振蕩減小。這主要是由于氣動阻尼的存在,也表明氣動力有輔助折疊變形的作用。

從圖6中可以看出,在氣動力的作用下,隨著來流速度的增加,作用在子結構B上的合力、合力矩,以及作用在子結構C上的力、力矩均呈衰減振蕩。考慮氣動力時,氣動力與彈性位移相關,且是分布力,因此相對于重力產生的力矩而言,是較小的,因此與柔性機翼的結果類似。由于氣動阻尼的存在,力與力矩均有所減小。在一定的來流速度范圍內,氣動力有助于機翼的折疊變形。

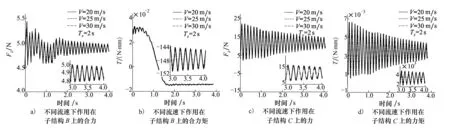
圖6　柔性機翼在重力和氣動力作用下的力學響應

3結論

結合多體動力學中的浮動坐標系法與結構動力學中模態綜合法,本文建立了機翼折疊變形過程中的動力學控制方程,該控制方程考慮了一些非線性項,如與速度二次方有關的廣義慣性力,可以用于分析機翼在緩慢變形和快速折疊變形的瞬態響應。分析了機翼柔性對瞬態響應的影響。將有理函數近似導出的折疊變形運動中的非定常氣動力近似表達式引入到動力學控制方程中,分析了柔性機翼的瞬態氣動彈性響應。可以得出以下結論:

1) 運用浮動坐標系法與模態綜合法建立的折疊機翼動力學控制方程。該控制方程適用類似的多段機翼結構,并且可以改變約束方程,可以獲得不同變形方式下的瞬態響應;

2) 對機翼折疊變形過程越緩慢,得到的瞬態響應越平穩;對于柔性折疊機翼而言,柔性對機翼在折疊變形過程的瞬態響應影響較大;

3) 考慮氣動力時,在一定的流速范圍內,來流速度越大,在變形結束后翼尖位移響應的振蕩越小。因此氣動力在一定的程度上有助于機翼的折疊變形運動。

參考文獻：

[1]WilsonJR.MorphingUAVsChangetheShapeofWarfare[J].AerospaceAmerica,2004,42(2):28-29

[2]ScarlettJohnN,CanfieldRobertA.MultibodyDynamicAeroelasticSimulationofaFoldingWingAircraft[C]∥47thAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamicsandMaterialConference,Newport,RhodeIsland, 2006

[3]ReichGregoryW,BowmanJasonC,SandersBrian.DevelopmentofanIntegratedAeroelasticMultibodyMorphingSimulationTool[C]∥AIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamicsandMaterialConference, 2006,Newport,RhodeIsland

[4]王杰. 折疊翼飛行器氣動彈性與動力學仿真[D]. 南京：南京航空航天大學，2010

WangJie.AeroelasticityandDynamicsAnalysisonaFoldingWingMorphingAircraft[D].Nanjing,NanjjingUniversityofAeronuaticsandAstronautics, 2010

[5]EvgenySelitremmik,MotiKarpel.ComputationalAeroelasticSimulationofRapidlyMorphingAirVehicls[J].JournalofAircraft, 2012, 49(6): 1675-1686

[6]ZhaoYouhui,HuHaiyan.PredictionofTransientResponsesofaFoldingWingduringtheMorphingProcess[J].AerospaceScienceandTechnology, 2013, 24(1): 89-94

[7]BaumgarteJW.StabilizationofConstraintsandIntegralsofMotion[J].ComputerMethodsinAppliedMechanicsandEngineering, 1972(1): 1-6

[8]ShabanaAA.DynamicsofMultibodySystems[M].CambridgeUniversityPress,NewYork, 1998

[9]CraigRR,BamptonCC.CouplingofSubstructuresforDynamicAnalysis[J].AIAAJournal, 1968, 6(7): 1313-1310

收稿日期：2015-05-19

作者簡介：倪迎鴿(1987—),女，西北工業大學博士研究生,主要從事變體飛機一體化設計的研究。

中圖分類號：V271.4

文獻標志碼：A

文章編號:1000-2758(2016)03-0418-06

Transient Dynamic Response Analysis of a Wing in the Folding Motion

Ni Yingge, Hou Chi, Wan Xiaopeng, Zhao Meiying

(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:A set of equations which govern the time evolutions of a wing in the folding motion are developed to predict the transient dynamic responses by integration the floating frame approach in multibody dynamics with component modal synthesis in structural dynamics. The developed equations are further integrated with unsteady aerodynamics in the folding motion which is obtained by rational function approximation to carry out the transient dynamic responses with time-varying aerodynamics. Results demonstrate that the transient responses are more stable in a slower folding motion. The flexible wing has a great effect on the responses. Within a certain flow velocity a greater velocity means a smaller oscillation of the tip displacement and contributes to the folding motion.

Keywords:folding wing;transient dynamic responses;rational function approximation;floating frame approach;component modal synthesis;unsteady aerodynamics; dynamics; time varying systems