一類算子方程邊值問題的可解性

金啟勝

(安慶職業技術學院 公共基礎部，安徽 安慶 246003)

?

一類算子方程邊值問題的可解性

金啟勝

(安慶職業技術學院 公共基礎部，安徽 安慶 246003)

摘要：利用泛函的極小函數研究了一類算子方程邊值問題的可解性，得到對稱正算子方程有解的充分必要條件，以及泛函存在極小函數的充分條件。并對三種邊值問題的實例進行了驗證。

關鍵詞：對稱算子；正算子；正定算子；極小函數；Green第二公式

0引言

(1)

的線性定解問題。其中L,Lj是線性微分算子，f(x)是已知函數。

此線性定解問題對應于Hilbert空間H中一個線性算子方程Au=f(x)，其中A的定義域DA是H的一個線性稠密子集合。比如當H=L2(Ω)時，取

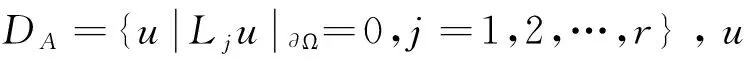
Au的值與Lu的值在DA上是相同的。故求解方程(1)就是在DA上求解方程：

Au=f(x)。

定義1對任意的u,v∈DA，如果算子A滿足等式(Au,v)=(u,Av)，則稱A為對稱算子。

定義2設A是定義在Hilbert空間H的某一線性稠密子集DA上的線性算子，如果對DA中任意元素u，有(Au,u)≥0且等號成立時當且僅當u=0，則稱A為正算子。

定義3設A是DA上線性算子，如果存在常數γ>0，對任意的u∈DA都有(Au,u)≥γ2(u,u)，則稱A是DA上的正定算子。

在DA上引入新內積[u,v]=(Au,v)；和新內積對應的新范數記為：

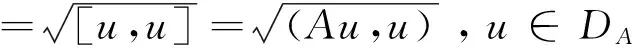
根據算子A的正定性可知，原空間H和新空間H*的范數滿足：‖u‖‖u‖*。

2主要結論及證明

定理1 若A為正算子，則方程Au=f(x)至多有一個解u∈DA。

證明如果Au=f(x)有兩個解u,v，則Au=f(x)，Av=f(x)。二式相減得：

A(u-v)=0，所以(A(u-v),u-v)=0，又A為正算子，所以u-v=0，即u=v。

定理2設A為對稱正算子，若方程Au=f(x)有解u0∈DA，則u0必是泛函：

F(u)=(Au,u)-2(u,f)

(2)

的極小函數；反之，若u0∈DA是F(u)的極小函數，則有Au0=f(x)。

證明泛函F(u)和算子A的定義域相同。設Au0=f(x)，對任何v∈DA，v≠u0，令η=v-u0，因為DA是線性子集合，則η∈DA。根據算子A的對稱性得：

F(v)=F(u0+η)=(A(u0+η),u0+η)-2(u0+η,f)，

=(Au0,u0)+2(Au0,η)+(Aη,η)-2(u0,f)-2(η,f)，

=F(u0)+2(Au0-f,η)+(Aη,η)=F(u0)+(Aη,η)>F(u0)。

所以u0必是泛函F(u)=(Au,u)-2(u,f)的極小函數。

反之，設u0∈DA是F(u)的極小函數，η∈DA，則u0+λη∈DA，λ∈R。當

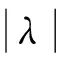
如果Au0-f∈DA，取η=Au0-f，所以Au0-f=0，即Au0=f(x)。

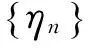
ηn→Au0-f在H中成立，于是由(Au0-f,ηn)=0得(Au0-f,Au0-f)=0，所以Au0=f(x)，即u0是算子方程Au=f(x)的解。

定理3若A為對稱正定算子，則泛函F(u)在H*中存在極小函數。

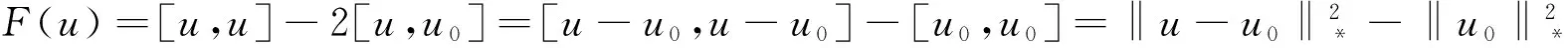
?u∈H*。

所以泛函F(u)在u=u0時取得極小值。

3應用舉例

設Ω是Rm(m≥2)中有界區域，對于位勢方程-Δu=f(x),x∈Ω，考慮三種邊值問題的邊界條件：

其中σ0是正常數，ν是?Ω的單位外法向。求解這三類邊值問題轉化為求對應的泛函的極小函數問題。這就必須先驗證各自對應的算子為對稱正算子。取Hilbert空間為L2(Ω)。

(1)對應于Dirichlet問題的算子-Δ定義域為：

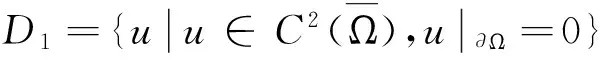
若u,v∈D1，由Green第二公式得：

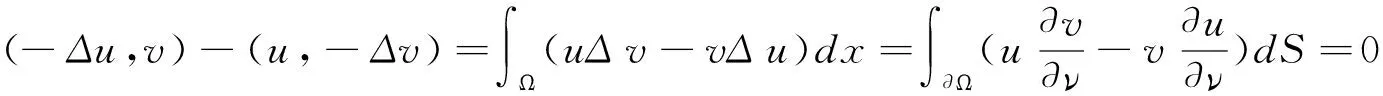
所以-Δ是D1上的對稱算子。另外，當u∈D1時，有：

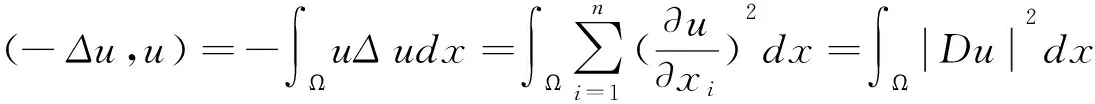
當且僅當u恒等于常數時等號成立。由u的連續性及邊界條件得在Ω上u≡0。所以-Δ是D1上的對稱正算子。

(2)對于Neumann問題，不是對任何函數都是可解的。因為對方程-Δu=f(x),x∈Ω兩邊在Ω上積分，運用基本解公式及邊界條件得：

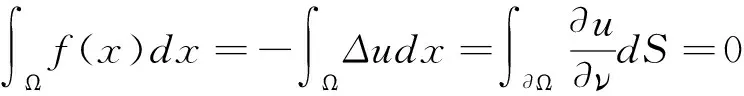
另外，任何一個解加上一個常數后仍然是問題的解，為了保證解唯一就必須附加條件。比如所求解滿足∫Ωudx=0，顯然此時的解唯一。選擇對應于Neumann問題的算子-Δ定義域為：

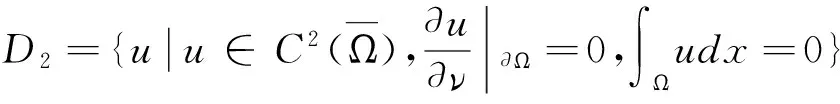
(3)對應于Robin問題的算子-Δ定義域為：

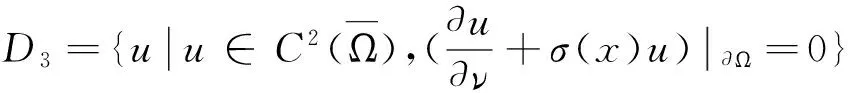
(-Δu,v)-(u,-Δv)=-∫Ω(vΔu-uΔv)dx，

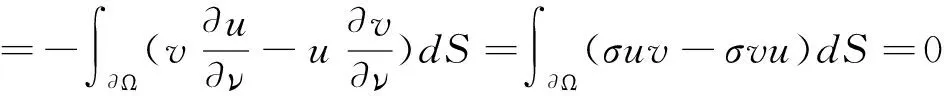
所以-Δ是D3上的對稱算子。另外，當u∈D3時，有：

(-Δu,u)=-∫ΩuΔudx，

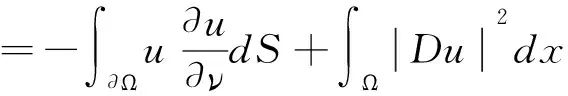
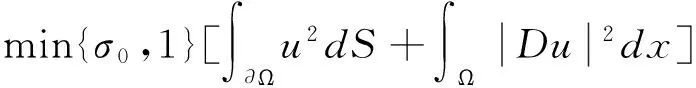
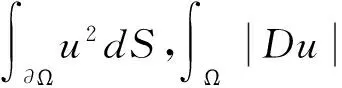
(-Δu,u)=0?u≡0，所以-Δ是D3上的對稱正算子。

所以根據定理2得，(1)、(2)、(3)三問題的求解依次化為下列泛函：

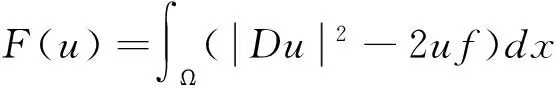
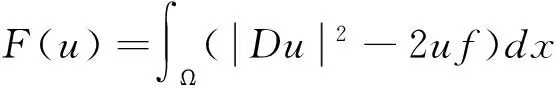
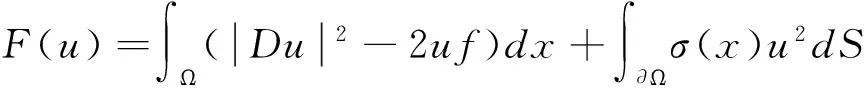
分別在集合D1，D2，D3上求極小函數問題。

最后，我們驗證泛函的極小函數存在問題，即驗證算子-Δ在對應的線性集合上是正定的。對于本文中提到的三種邊值問題，我們只驗證Robin問題的算子-Δ是D3上的正定算子。對于算子-Δ在D1，D2上是正定的可類似進行驗證。

設區域Ω在第一象限，且完全含于閉域Ω1={0xa,0yb}之內。根據不等式(-Δu,u)

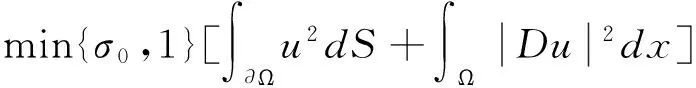
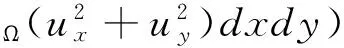
為此我們令u=gv，其中v是未知函數，g是待定函數。

≥-v2gΔg+(v2ggx)x+(v2ggy)y。

將上面不等式在Ω上積分，并且利用散度定理得到：

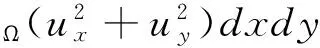
-?Ωv2gΔgdxdy?，即

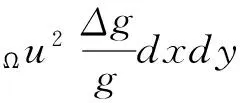
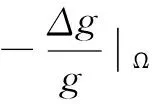
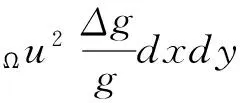
c1?Ωu2dxdy?，取，即得不等式

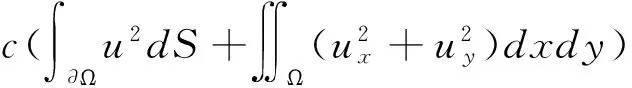
所以，算子-Δ是D3上的正定算子。

參考文獻：

[1]陳祖墀.偏微分方程[M].合肥:中國科學技術大學出版社,2004.

[2]曾志芳,朱傳喜.半序空間中三元算子方程的可解性問題的研究[J].系統科學與數學，2014,34(5):582-588.

[3]馮育強,劉三陽.半序空間中一類算子方程的可解性[J].數學學報，2003,46(2):411-416.

[4]姚福元.一類算子方程的可解性[J].科學通報，1991,36(11):804-806.

責任編輯：程艷艷

Solvability of Boundary Value Problem of a Class of Operator Equations

JIN Qisheng

(Department of Public Fundamental Courses, Anqing Vocational and Technical College, Anqing 246003, China)

Abstract：This paper discusses the solvability of boundary value problem of a class of operator equations by using the minimum function, getting the necessary and sufficient conditions for symmetric positive solutions to operator equations, as well as the sufficient condition for the existence of the minimum function in functions. And three kinds of boundary value problems are verified by examples.

Keywords：symmetric operator; positive operator; positive definite operator; minimum function; second formula of Green

收稿日期：2016-04-29

基金項目：2015年安徽省質量工程項目(2015jyxm539)；2016年安徽省自然科研項目(KJ2016A447)

作者簡介：金啟勝(1972-)，男，安徽桐城人，副教授，碩士，主要從事微分方程方面研究。

中圖分類號：O175.2

文獻標志碼：A

文章編號：1009-3907(2016)06-0054-04