基于循環修正的黑龍江省各主要城市綜合競爭力綜合評價方法研究

馬　丹，于海芳，徐　偉

(1.大慶師范學院 教師教育學院，黑龍江 大慶 163712；2.朝陽師范高等專科學校 數學計算機系，遼寧 朝陽122000)

?

基于循環修正的黑龍江省各主要城市綜合競爭力綜合評價方法研究

馬丹1，于海芳2，徐偉1

(1.大慶師范學院 教師教育學院，黑龍江 大慶 163712；2.朝陽師范高等專科學校 數學計算機系，遼寧 朝陽122000)

摘要：針對城市競爭力評價中存在的單一方法評價結果不一致的問題，對黑龍江省12個主要城市的11項指標，分別采用綜合指數法、層次分析法、主成分分析法和因子分析法進行綜合評價和排位；再以Spearman等級相關系數為檢驗標準，利用平均值法、Board法、Copealand法、模糊Board法對單一模型進行組合，反復迭代，得到黑龍江省各主要城市綜合競爭力的綜合評價和排序。

關鍵詞：主觀賦權法；客觀賦權法；Spearman相關系數；循環修正

0引言

20世紀80年代以來，對于城市競爭和城市競爭力的研究日益受到國內外學者的關注。他們不僅深入探討和闡述了城市競爭力的概念、內涵與特征，而且設計了一些城市競爭力的指標體系，在城市競爭力量化評價方法模型的研究和實踐中也取得了很多成果。這些評價方法根據賦權方法的不同，大致可分為兩類，一類是主觀賦權法主要有綜合指數法、層次分析法、專家評價法等，一類是客觀賦權法主要有主成分分析法、因子分析法等。由于權重的主觀任意性，常導致一種方法的評價結果很難令人信服，而且不同方法對同一對象的評價結果往往存在差異，為解決此問題，本文在研究相關文獻的基礎上，分別采用兩種主觀賦權法綜合指數法[1]、層次分析法[2]和兩種客觀賦權法主成分分析法[3]、因子分析法[4]，并將這四種方法分別采用目前常用的平均值法、Board法、Copealand法、模糊Board法[5]進行組合，可實現不同評價方法的優勢互補，通過用組合評價方法對不同的單一評價方法得到的不同評價結果進行修正，保證了不同評價方法結果的一致性。

1城市綜合競爭力評價指標體系

以《黑龍江省2013年統計年鑒》為基礎，利用SPSS統計軟件對黑龍江省12個主要城市進行評價和分析，選取11項指標構建評價體系：X1：地區生產總值(億元)，X2:固定資產投資總額(億元)，X3：社會消費品零售價總額(億元)，X4：公共交通客運總量(萬人次)，X5：衛生機構床位數(張)，X6：普通高等學校在校生數，X7：進口總額(萬美元)，X8：外商直接投資使用金額(萬美元)，X9：建成區面積(平方公里)，X10：城市園林綠地面積(公頃)，X11：人均城市道路面積(平方米)。

2循環修正的綜合評價步驟

(1)利用單一的評價方法。即綜合指數法、層次分析法、主成分分析法、因子分析法得到不同的評價結果和排序；

(2)對不同的方法得到的結果進行Spearman等級相關系數檢驗，若通過檢驗，則結果為最終結果；若不通過檢驗則轉入(3)；

(3)分別用平均值法、Board法、Copealand法、模糊Board法對單一評價結果進行綜合評價，得到評價結果及排序；

(4)對綜合評價結果進行Spearman等級相關系數檢驗，若通過檢驗，則結果為最終結果；若不通過檢驗則轉入(3)，直至評價結果通過Spearman等級相關系數檢驗，且4種組合評價的結果趨于一致。

3單一評價模型

對原始數據進行標準化處理，分別采用綜合指數法、層次分析法、主成分分析法、因子分析法對黑龍江省各主要城市的綜合競爭力進行評價，結果見表1。

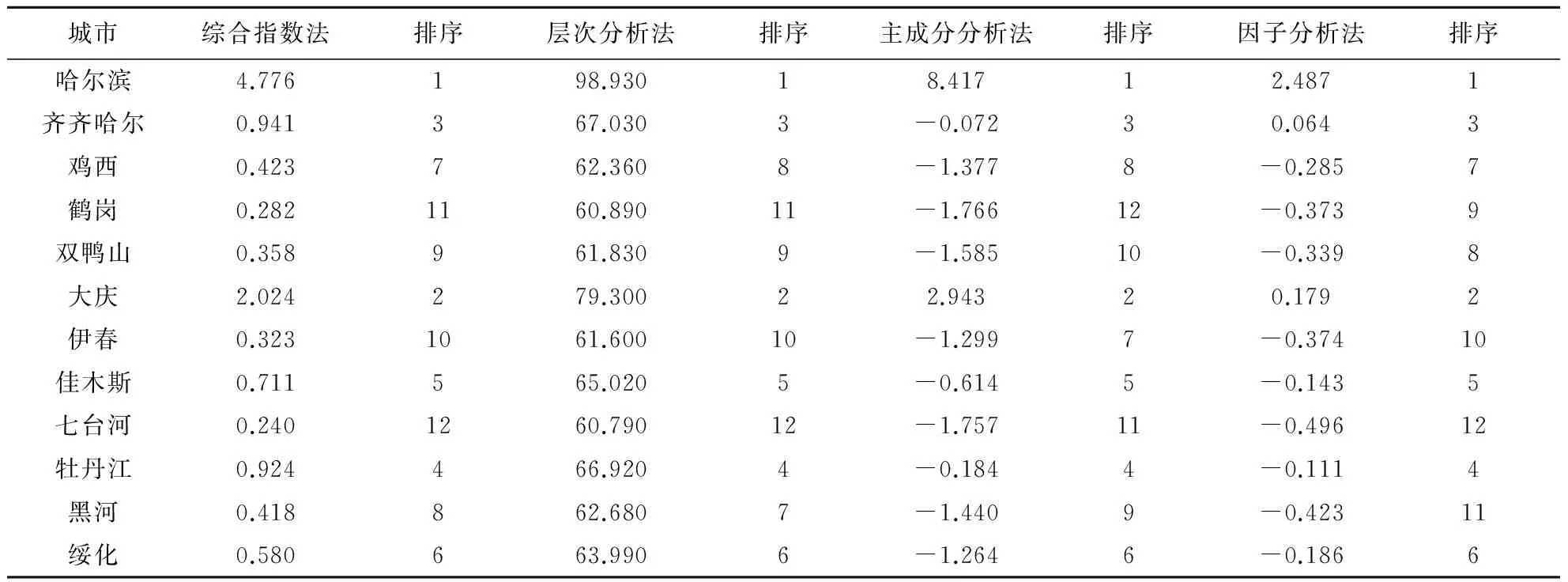
表1　各模型得分及排名

4循環修正的組合評價

4.1四種評價方法的一致性檢驗

提出假設H0ij：兩種方法不相關；H1ij：兩種方法正相關(i,j=1,2,3,4;i≠j)

Spearman等級相關系數公式為：

(1)

其中，di為兩種排序的等級差。

通過對數據的處理，得到四種評價方法的相關系數矩陣：

由顯著水平α=0.05，cα=0.536，在上述的矩陣中，rij>cα，沒有理由接受H0，即四種方法正相關，具有一致性。

4.2平均值法

1)將排序名次轉換成得分，利用排序打分法

Rij=n-rij+1，

(2)

其中，rij:i=1,2,···,12;j=1,2,3,4為第i個城市在第j種方法下的排位。

2)平均值法組合評價

(3)

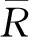
(4)

4.3Board法

Board法是一種少數服從多數的方法，，若評價方法認為優于城市j的個數多于城市j優于城市i的個數，記為xisxj。

定義Board矩陣

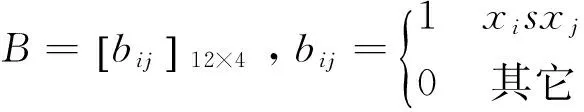
(5)

組合評價值為

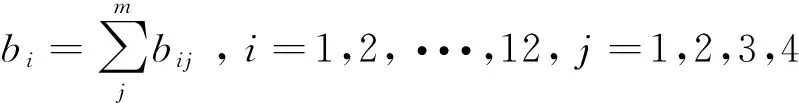
(6)

若兩個城市組合評價值相等，如方法2.1中標準差小為優。(表2)

4.4Copealand法

4.5模糊Board法

1)計算隸屬度

(7)

注：xij為地區i在第j種方發現的得分；μij為地區i在第j種方法下的隸屬度。

2)根據城市的排位h及隸屬度μij定義模糊頻數

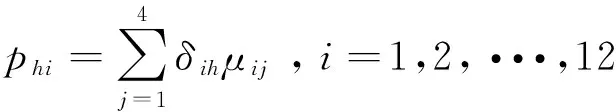
(8)

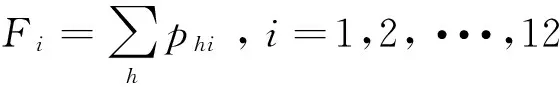
(9)

3)將排位h轉化為得分Qh，

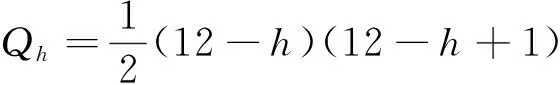
(10)

4)計算模糊Borda數得分yi，按得分yi大小重新進行排序。

yi=∑WhiQhi，i=1,2,···,12(表2)　(11)

表2(續)

表2可見，運用組合評價法進行第1次組合，評價結果仍有差異，需要進行第二次迭代修正。計算Spearman等級相關系數，可見不同方法之間兩兩相關，可以通過一致性檢驗，因此進行第二次組合，結果見表3，從表3可見，不同組合評價方法的結果完全相同。綜合競爭力由強到弱的排序為：哈爾濱、大慶、齊齊哈爾、牡丹江、佳木斯、綏化、雞西、黑河、雙鴨山、伊春、鶴崗、七臺河。

表3　第二次組合評價得分及排序

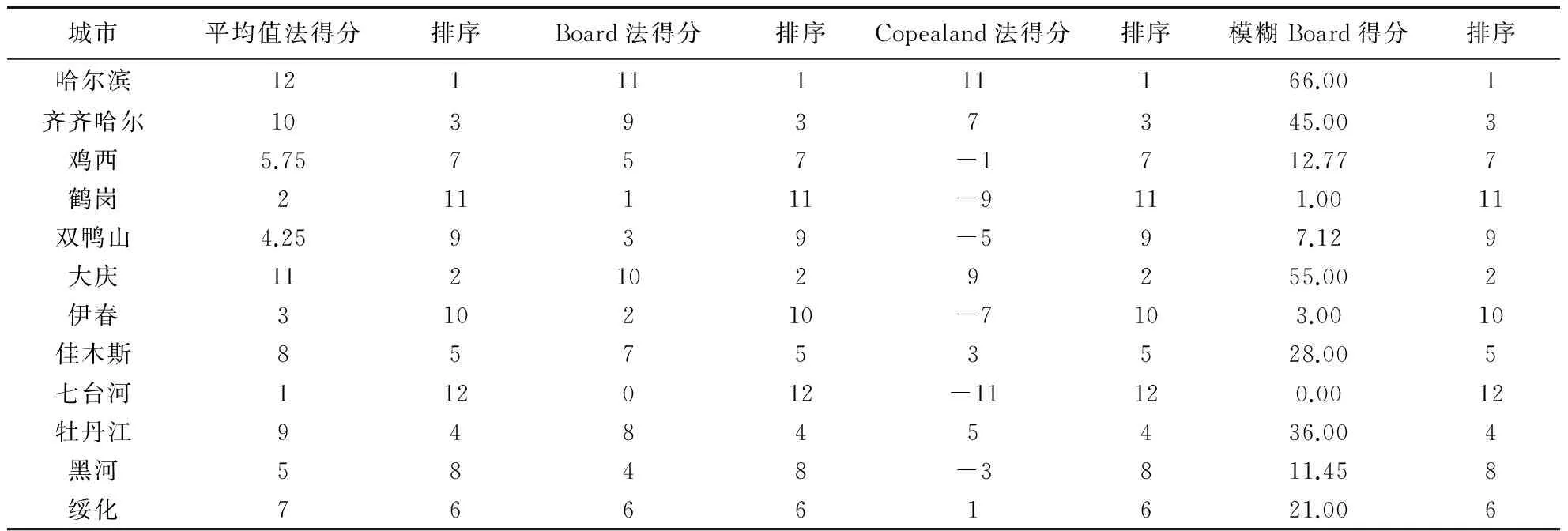
城市平均值法得分排序Board法得分排序Copealand法得分排序模糊Board得分排序哈爾濱12111111166.001齊齊哈爾103937345.003雞西5.75757-1712.777鶴崗211111-9111.0011雙鴨山4.25939-597.129大慶1121029255.002伊春310210-7103.0010佳木斯85753528.005七臺河112012-11120.0012牡丹江94845436.004黑河5848-3811.458綏化76661621.006

5模型與評價

本文采用了循環修正的組合評價法對黑龍江省各主要城市的綜合競爭力進行了評價。這種方法相對于單一評價模型優勢在于，克服了主觀賦權法與客觀賦權法的不足，評價結果進行了多次組合最終得到了一致的排名結果，解決了單一方法結果具有差異性的問題。使結果更具科學性和可參考性。從評價結果看到，黑龍江省各主要城市的綜合競爭力由強到弱的排名為：哈爾濱、大慶、齊齊哈爾、牡丹江、佳木斯、綏化、雞西、黑河、雙鴨山、伊春、鶴崗、七臺河。這與人們直觀排序基本一致。從綜合評價得分上看，各地區差異較大，這說明黑龍江省各城市的綜合競爭力情況很不平衡。為縮小差距，黑龍江省可采取相應政策，以協調各地區的發展情況。

[參考文獻]

[1] 劉艷春,高立群.組合評價模型在遼寧省主要地區綜合經濟實力評價中的構建及應用[J].數學的實踐與認識,2005,35(3):44-50.

[2] 鄧雪,李家銘,曾浩健，等. 層次分析法權重計算方法分析及其應用研究[J]. 數學的實踐與認識,2012,42(7):93-100.

[3] 馬丹,蔡若男,喬興. 基于集成綜合評價法和聚類分析法的綜合評價方法[J]. 數學的實踐與認識,2013,43(11) :102-106.

[4] 陳萍. 黑龍江省中心城市競爭力分析[J].哈爾濱師范大學自然科學學報，2006(5):109-112.

[5] 劉艷春. 一種循環修正的組合評價方法[J]. 數學的實踐與認識,2007,37(4) :88-94.

作者簡介：馬丹(1981-)，女，遼寧鞍山人，講師，從事多元統計分析方向研究。

中圖分類號：O212.4

文獻標識碼：A

文章編號：2095-0063(2016)03-0081-04

收稿日期：2015-3-26

DOI 10.13356/j.cnki.jdnu.2095-0063.2016.03.020