影子變化規律的數學模型及視頻信息的確定

楊坤++鄭繼明++劉慧鵬++肖敏

摘 要：通過分析被攝物體的太陽影子變化規律，建立非線性模型，確定視頻拍攝地點和日期信息。采用多項式擬合確定當地出現影長最短的時刻，并通過與北京時間比較，求得被攝物體所處經度；利用影子頂點的坐標數據給出太陽方位角和影子長度隨時間的變化規律，并反解出被攝物體所處緯度和拍攝日期。實例表明，在參照物體尺寸未知的情況下，該方法也能實現拍攝信息的提取。

關鍵詞：多項式擬合；影子長度；太陽方位角；非線性模型

中圖分類號：O13 文獻標識碼：A DOI：10.15913/j.cnki.kjycx.2016.14.009

在智能手機等電子產品普及的今天，拍攝視頻已經不是少數專業人員的工作。在生活中，人們喜歡拿起手中的手機記錄下一段視頻。一般情況下，使用手機等電子產品拍攝的視頻會根據手機的定位功能和時間記錄下視頻拍攝的地點和日期。但是在實際生活中，視頻在傳播過程經常會出現拍攝信息不同程度丟失的情況。與此同時，在分析視頻數據時，拍攝信息的有無直接影響視頻數據分析的結果。目前，對于傳統拍攝信息的確定，有一些比較成熟的方法，比如文獻主要利用網絡攝像機拍攝目標圖像，多傳感器采集目標數據，經過處理后送入攝像機進行三維定位運算，從而獲得地址信息的方法。然而，該方法需要大量的傳感器來采集數據，對于已經拍攝好且失去了拍攝信息的視頻來說，顯然不適用。目前，很多視頻拍攝設備都內置了世界主要的幾種衛星定位模塊，但是該模塊記錄的信息在實際的視頻傳播中很容易丟失或者被人為地刪除。要恢復丟失的拍攝信息，需要具備較高的技術水平。因此，根據視頻中已有的信息來獲得拍攝地點和日期等信息，對于解決拍攝信息不同程度丟失的問題具有一定的應用價值。本文運用太陽影子定位技術，通過分析視頻中被攝物體的太陽影子變化規律，給出一種確定視頻拍攝地點和日期的方法，在一定精度范圍內恢復結果較為理想。

1 模型的準備

為分析被攝物體的太陽影子變化規律，先給出建模的一些假設：①在一天內，太陽直射地球的緯度保持不變，即赤緯角保持不變；②閏年對赤緯角沒有影；③太陽直射在地球上的光都是平行光；④忽略極端天氣對太陽方位角的影響；⑤一般情況下，鏡頭所在平面與被攝物體平行。

為計算物體影子長度，記ts為太陽時（單位為h），n為日期序號，并設n=1表示1月1日，n=365表示12月31日，則時角ω和赤緯角δ的計算公式分別為：

太陽高度角α是以太陽為幾何中心的視盤面與理想地平線的夾角。下面設被攝物體的長度和影子長度分別為H和L，且物體所處的緯度為φ，則太陽高度角的正弦可近似表示為：

由式（3）知，如果已知太陽高度角α ，則根據

2 模型的建立與求解

2.1 影子頂點視頻中坐標與世界坐標的轉換

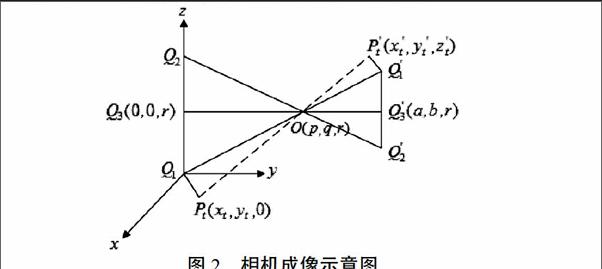
對于視頻數據，由于經過相機的成像變形，因此不能簡單地認為視頻中的影子長度與實際影子的長度有比例關系。建立Q1-xyz的世界坐標，如圖2所示。設攝像機的光心坐標為O（p，q，r），則視線方向 （-p，-q，O），其中，Q3（O，O，r）為鏡頭沿著視線方向對應被攝物體上的點。

圖2 相機成像示意圖

我們假設k為被攝物體真實長度與像長的比值，即物像比，則：

. （5）

根據三角形相似定理，可得到像平面的點法式方程為：

. （6）

由于Pi，O，Pi'三點共線，且從鏡頭沿著視線反方向對應于像平面被攝物體上的點Q3'（a，b，r）在像平面上，因此，由式（5）和（6）可得：

于是，被攝物體在t時刻的影子長度為：

2.2 經度、緯度和日期求解模型

2.2.1 經度求解模型

生活經驗和研究數據表明，在一天內，影子長度關于當地時間的變化曲線呈現“上午和下午影子長度在對稱時刻是相等的”，滿足開口向上的一元二次函數圖像的特征。因此，可以根據已有數據進行多項式擬合。根據多項式曲線擬合原理，求解出關于影長和時間的擬合函數為：

其中，a>0，b，c均為常數。由式（10）可知，被攝物體

的影子在 時的影長最短。

假設某地被攝物體影長最短的時刻出現在當地時間正午12：00，物體所處的經度為φ，根據當地時間和北京時間tsb（東經120°時間），則可以得到經度為：

2.2.2 緯度和日期求解模型

根據式（4）影子長度與各個參數關系的模型可知，要求得影子的長度，必須知道被攝物體的長度。因此，需要在被攝物體長度未知的情況下，建立一個與被攝物體長度無關的模型。為此，在式（4）的基礎上采用了不同時刻影長兩兩相比的方式，避開了被攝物體長度對模型求解的影響。具體做法如下。

根據式（4）影子長度與各個參數關系的模型，在t1，t2時刻的影長分別為：

式（14）與被攝物體的長度無關。

下面利用太陽方位角來確定緯度和日期。設太陽方位角為A，則 .于是，在t′=t1-t2的時間段中，太陽方位角的增量可以表示為：

同時，在坐標系中oxyz中，如果已知t1，t2時刻影子頂點坐標分別為（Xt1，Yt1）和（Xt2，Yt2），則由圖3可得：

式（15）和（17）給出了在t′時間段中太陽方位角增量ΔA的兩種計算方法。在實際計算過程中，由于t′的時間段中太陽方位角增量ΔA的實際值與理論值存在一定的偏差，因此不能用ΔA根據坐標求解得到的實際值代替理論值，需要再帶回式（15）中反解出緯度和日期。本文根據實際情況，建立ΔA的實際值與理論值的相對誤差最小模型，再利用式（15）反解出緯度和日期，具體解法如下。

根據式（15）和（17），對ΔA的實際值和理論值做差，并取絕對值的平方，得到的目標函數為：

再結合式（1）（2）（3）和（14），可以得到緯度φ和日期n應滿足的約束條件，并可以建立以下非線性優化模型：

模型（19）的求解方法如下：①取任意時刻t1，t2，根據圖2計算出L t1，L t2，L t′及ωt1，ωt2；②將所得計算數據代入模型（19）的目標函數和約束條件中，得到只含變量φ和n的優化問題；③由于存在日期關于夏至、冬至日對稱而引起的多解，因此根據夏至日（n=173）、冬至日（n=365）將n的取值范圍分為兩段，再根據文獻[5]和[6]的思想，利用LINGO軟件編程求解，分別得到目標函數值最小時φ和n的取值；④對多組數據，重復上述步驟，對合理的值取平均值后得到最后結果。

注：根據地球公轉運動規律，太陽的直射緯度在南北回歸線之間，無論是在北半球，還是在南半球，在一年中，同一地點被攝物體影子出現相同運動規律一定會出現兩次，且這兩次的日期關于夏至日或者冬至日對稱。因此，求解的結果會出現由于日期關于夏至、冬至日對稱而引起多種拍攝日期與地點組合的可能結果。

3 實例應用

根據2015年高教社杯全國大學生數學建模競賽A題的附件4視頻數據，應用本文提出的方法確定視頻拍攝地點和日期信息。先建立以一條過被攝物體且平行鏡頭平面的直線為x軸，以垂直于x軸背對鏡頭方向的直線為y軸的坐標系，如圖4所示。

再運用MATLAB軟件的VideoReader函數，對視頻每隔4 min提取一幀，求解得到不同時段的影子端點的像坐標。根據（7）（8）和（9）式可以求得視頻時間換算與端點影長的關系，部分數據如表1所示。

對表1中的數據運用MATLAB軟件進行多項式擬合，再利用式（11）求得該拍攝地點的經度為東經114°29'10"。最后根據2.2.2節中的求解方法，對式（19）利用LINGO軟件編程求解，得到視頻拍攝地點的緯度為北緯26°44'9"，拍攝日期為7月15日或5月29日。

4 結束語

根據被攝物體影子一天中隨時間的變化可以得到該影子測量點的地理位置信息，這對當前比較熱門的研究課題——影子定位技術有很好的利用價值。利用相機小孔成像的知識，從一段含有影子軌跡的視頻中讀取出視頻拍攝的日期和地理位置，為利用太陽影子定位技術提供可行的理論依據。

參考文獻

[1]邵撼薪.基于Davinci平臺的目標圖像定位系統[D].昆明：昆明理工大學，2014.

[2]邢佩旭.世界主要幾種衛星導航定位系統的現狀與發展[J].港工技術，2003（1）.

[3]劉海波，王建芳，于海芹.太陽能工程中幾種相關角度的計算及應用[J].陽光能源，2013，10（2）.

[4]游步東.關于軸測體視投影的原形[J].南昌大學學報（工科版），1995，17（1）.

[5]葉留青，常興邦，張曙光.非線性規劃問題的全局最優解的充要條件及其算法模型[J].河南科學，2005，23（5）.

[6]龍強.一種求解帶等式約束非線性規劃問題全局最優解的方法[J].重慶文理學院學報（自然科學版），2010，29（1）.

〔編輯：劉曉芳〕