基于動態扇區的空域與飛行流量兩階段協同規劃模型及算法

姚頔, 王瑛

(1.空軍工程大學 裝備管理與安全工程學院, 陜西 西安　710051; 2.國家飛行流量監控中心, 北京　100094)

?

基于動態扇區的空域與飛行流量兩階段協同規劃模型及算法

姚頔1,2, 王瑛1

(1.空軍工程大學 裝備管理與安全工程學院, 陜西 西安710051; 2.國家飛行流量監控中心, 北京100094)

摘要：針對管制扇區動態規劃與飛行流量時空調配的耦合問題，考慮運行容量、效率等目標，建立了兩階段協同規劃模型及求解框架。第一階段根據自然航路點和流量分布，結合Voronoi圖與圖論模型構建有限元加權圖拓撲抽象，以均衡管制負荷和減少協調移交負荷為目標，基于遺傳算法適應性生成扇區結構；第二階段綜合等待和改航策略，以緩解區域總延誤和該區域造成的區域外延誤為目標，同時兼顧均攤延誤和減少延誤架次，在區域內容量約束和其他區域對該區域的流控約束下，基于NSGA-II進行流量時空優化。按照優先級順序實施策略流程，為緩解空中交通擁堵探索綜合施策框架。仿真結果表明，所提出的模型算法可為提升空管運行品質提供輔助決策支持。

關鍵詞：飛行流量管理；空域管理；空域動態配置；動態扇區；兩階段協同規劃

航空器在空域飛行形成空中交通，空管以保障航空運行安全高效和空域使用科學精益為目標，空中交通需求為基本輸入，服務容量為約束，符合間隔標準的有序交通流為輸出，在管制服務基礎上逐漸衍生出了空域管理和飛行流量管理功能，推動空管從戰術性或被動反應式系統向戰略性或前攝式系統發展。為應對日益突出的飛行效率與空域資源配置矛盾，歐美空管系統在流量管理(air traffic flow management,ATFM)實踐的同時，不斷探索空域動態配置(dynamic airspace configuration,DAC)，占據著運行概念與技術應用的制高點。國際空管一體化趨勢與無縫運行剛性需求與日俱增，對我國運行方式與效能提出更高要求，研究DAC和ATFM的協同規劃框架方法，對空管運行實踐具有重要指導意義。

1相關研究

DAC方面，歐美強調空域結構動態調整以適應具體交通流的運行理念，并進一步設想在未來“自由飛行”條件下僅在不能滿足動態航跡需求的區域建立固定航路結構[1]。在不區分軍民航空域屬性的一體化統籌統配模式下，管制扇區的動態規劃是DAC的核心，現有研究主要集中在模型選擇上，包括基于區域元胞(region model/cell model)[2-3]、計算幾何Voronoi圖(Voronoi diagram model)[4-5]、圖論(graph model)[6-7]和軌跡(flight trajectory model)[8]等建模方法。區域建模將空域均勻分割為一組多邊形元胞(如文獻[2-3]采用正六邊形)并進行管制負荷或空域復雜度測度，通過聚類算法[2]、生長算法[3]等將元胞網格組合成負荷相對均衡的扇區。與之類似，Voronoi圖建模也以平衡負荷為目標，隨機生成節點[4]或繼承導航臺等航路點位置先驗[5]作為空間目標簇，以空間目標的Voronoi多邊形為初始拓撲，基于遺傳算法[4]、模擬退火算法[5]等組合生成扇區。圖論建模以機場、航路點為節點，航段為邊，管制負荷為點、邊權重構建加權圖模型，基于遺傳算法[6]、譜聚類算法[7]等切分形成扇區邊界。軌跡建模比較典型的是以動態密度為性能測度，通過k均值算法聚類航跡實現空域剖分[8]。Li Jinhua結合區域元胞和圖論建模[9]，將矩形元胞覆蓋航路，在繼承航路結構同時，顯著降低了計算復雜度。

ATFM方面，按主要發展軌跡分為單機場地面等待模型(single airport ground holding problem, SAGHP)[10]、多機場地面等待模型(multi-airport ground holding problem, MAGHP)[11]和(使用改航策略的)流量網絡優化模型(air traffic flow network optimization problem,ATFNOP/air traffic flow network optimization with rerouting problem,ATFNORP)[12-15]。早期聚焦機場交通擁堵，Odoni首先系統闡釋了SAGHP；Bertsimas和Odoni考慮機場間運行關聯性和延誤傳播效應，建立了MAGHP[11]。隨著研究從以機場為核心向空域全網演進，Bertsimas和Stock將空域抽象為以機場、扇區為節點的扇區網絡，在機場和扇區容量約束下，優化航班起降時間[12]，并對改航問題建立了動態多任務網絡流模型[13]。Bertsimas、Lulli和Odoni進一步提出了BLO模型[14]，以延誤代價最小構造超線性目標函數實現延誤公平分配，綜合地面等待、空中等待、改航、調速等運行策略，并在約束中引入3類不等式，強化模型松弛的多面體結構。受其啟發，Alonso等提出混合0-1整數規劃模型[15]，將扇區網絡變為航路網絡，使之更貼近于實際。此外，Dell′Olmo和Lulli針對航路網絡設計了一種層次迭代模型[16]，上下2層分別用于航路流量“粗粒度”分配和航路上具體航班四維航跡“細粒度”優化。Daniel等考慮緩解空域擁堵程度與航班延誤雙目標相互沖突，提出了最小化管制負荷和均勻降低延誤的多目標優化模型[17]。上述模型解法涵蓋線性規劃方法[10]、拉格朗日松弛算法[11-15]、啟發式算法[16]和進化算法[17]。

總體看，兩方面研究自成體系，統籌耦合研究較少。本文主要研究扇區動態調整與流量時空分配的協同規劃模型算法。

2問題描述與建模

2.1基本思想

DAC與ATFM以流量需求與空域容量的動態協調平衡為紐帶，DAC負責科學設計并動態調整空域容量，ATFM負責充分利用空域容量、優化調配流量需求。

前瞻借鑒國際空管運行理念，結合我國運行實際，為降低求解難度，本文認為協同規劃應分階段實施，其策略手段具有以下優先級：①空域是空管職能載體與核心資源，改變以固定劃分、靜態使用為特征的空域管理模式成為必然趨勢。靜態扇區結構難以有效適配時變的飛行流分布，造成管制席位忙閑不均，制約了容量潛力挖掘，空管應以適應飛行流動態調整扇區構形為首要手段，盡量減少對航班運行的控制與調整。因此，設定根據初始飛行計劃實施DAC的優先級高于ATFM。②時空資源的相關性，決定了ATFM時隙路徑聯動分配難分解。但在實際運行中，改航受到嚴格控制；此外，除遇惡劣天氣、軍事活動、突發事件等造成空域容量驟降，一般空域用戶希望按照原定計劃路徑飛行，改航可能導致繞飛，帶來額外飛行成本。因此，先以初始飛行計劃使用等待策略進行時隙調整，如可改航再同時使用改航策略和等待策略。

2.2協同規劃框架

按照“模塊化分解”和“兩階段協同”思路，設計規劃基本流程示意如圖1所示。第一階段，根據目標區域基礎數據建立以機場與導航臺等自然航路點為節點、航段為邊的無向圖，以無向圖節點為空間目標簇生成Voronoi圖；將Voronoi有限元內與有限元間管制負荷作為點、邊權重，構建約簡加權圖；以均衡各扇區內管制負荷和減少扇區間協調移交負荷為目標，對有限元進行組合優化，適應性生成扇區。考慮時變扇區缺乏歷史數據，無法基于管制負荷歷史峰值的擬合準確測度容量上限，利用國家飛行流量監控中心系統空域仿真與評估子系統對第一階段生成扇區按間隔標準進行航跡仿真，輸出扇區內航段容量。第二階段在新扇區拓撲下，以緩解區域總延誤和該區域造成的區域外延誤為根本目的，綜合均攤延誤和控制延誤架次2種常用目標策略，以機場、航路容量和其他區域對該區域施加的限流措施為約束，基于“時空分治”思想，按照時隙調整先于路徑調整的原則，首先調整初始飛行計劃的起降時隙，如容量驟降需避讓相關空域則啟動改航調整路徑與起降時隙，對于改航觸發的流量時空分布變化，返回第一階段重新生成扇區劃分，吸收消解因容量不足導致的延誤。新扇區生成后，按間隔標準及受限航路限流標準仿真輸出各扇區航段容量，進而重新分配起降時隙。

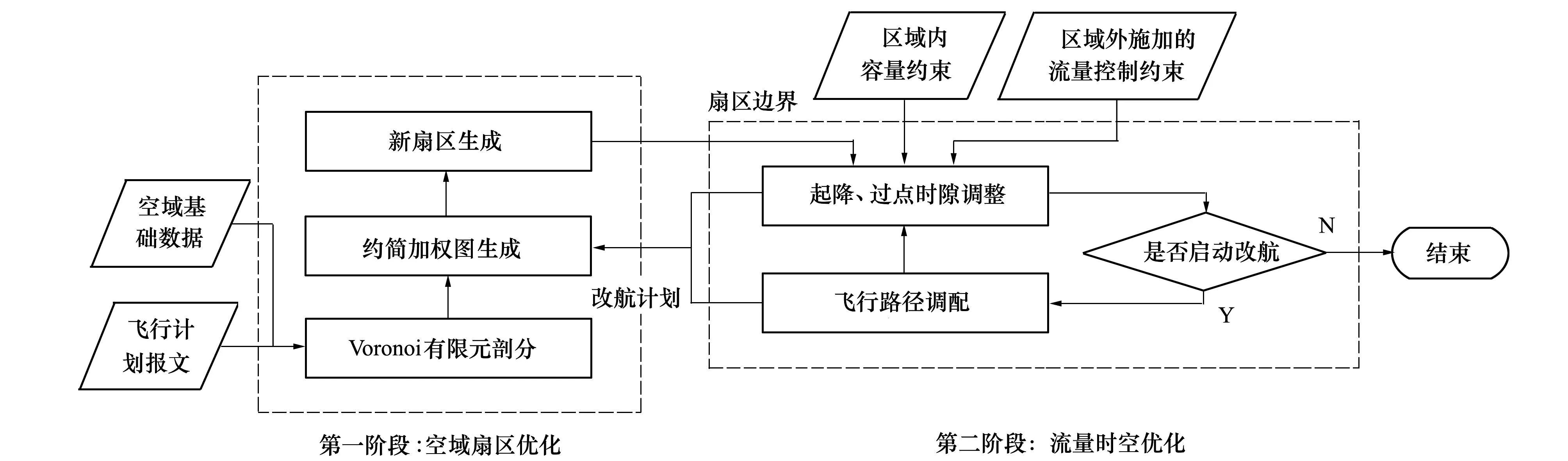
圖1　空域扇區與飛行流量協同規劃流程

2.3扇區優化模型

Voronoi圖(亦稱Dirichlet剖分)作為一種以等距離原則確定鄰接空間邊界的圖結構成為空域剖分的理想初始拓撲選擇，在自然繼承航路網結構基礎上，利于管制負荷統計。考慮基于管制操作計時、動態密度和空中交通復雜度的負荷測度在實際應用中的操作性問題，本文使用一種以管制架次-時間測度的負荷表達。

圖2給出了構建空域網絡有限元加權圖模型的一個示例。首先建立航路網無向圖Groute=(V,E),如圖2a)所示。其中,V={v1,v2,…,vNV}為機場與航路點集,|V|=NV,E={e1,e2,…,eNE}為航段集,|E|=NE。然后加載以V為空間目標簇的Voronoi圖Dvoronoi={D(v1),D(v2),…,D(vNV)},其中，D(vi)={x|d(x,vi)≤d(x,vi′),?vi′∈V},d為歐氏距離函數,D(vi)為vi的Voronoi多邊形。為避免航路交叉點與扇區邊界小于規定距離,以及機場與其進近導航臺劃分于不同扇區,對于相距過近的節點移除兩點之間的Voronoi多邊形邊界使之合并于一個有限元內,如圖2b)所示。相鄰Voronoi多邊形之間可能存在不止一條航段穿越,為簡化圖形,將穿越的多條航段合并表示為一條邊,并以點表示Voronoi多邊形,形成圖2c)所示約簡圖模型。

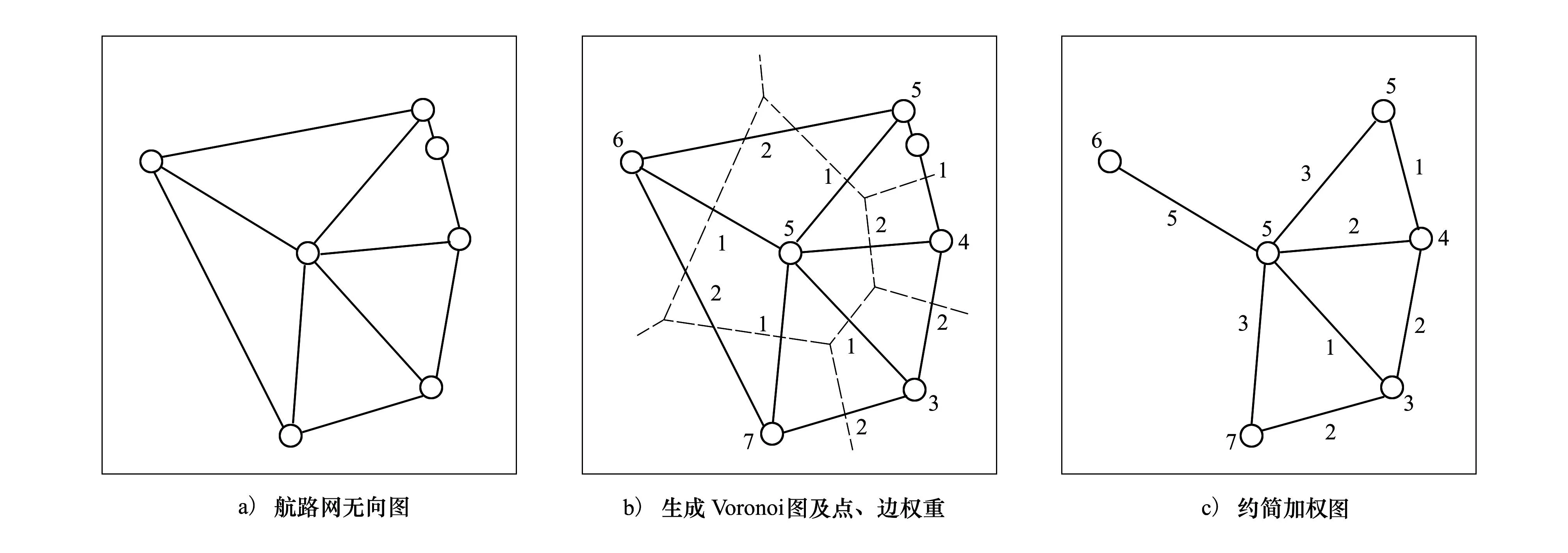
圖2　空域網絡有限元加權圖模型構建示意圖

D(vi)抽象的點權為

(1)

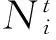
相鄰D(vi)與D(vi′)間邊權為

(2)

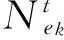
設扇區集S={sj},|S|=NS(sj、NS為變量),T時段內NS可按下式確定

(3)

為方便分析,將管制負荷簡化分解為監控負荷與協調移交負荷,基于上述約簡加權圖的點、邊權重測度方法,分別定義如下:

扇區sj的監控負荷為

(4)

相鄰扇區sj與sj′間的協調移交負荷為

(5)

定義指派變量xij,xij=1表示第i個Voronoi多邊形屬于第j個扇區,否則為0,則扇區sj監控負荷與協調移交負荷可表達為

(6)

(7)

以平衡各扇區管制負荷、最小化扇區間總協調移交負荷為目標,則目標函數為

(8)

從(8)式可明顯看出,扇區間總協調移交負荷越小,J越小;對于給定扇區間總協調移交負荷,各扇區管制負荷相等時,J最小。

約束條件包括

(9)

(10)

(11)

其中,(9)式確保每個Voronoi多邊形只能屬于一個扇區;(10)式確保每個扇區至少由一個Voronoi多邊形組成;(11)式為決策變量0-1整型約束。

此外,扇區構形須在滿足幾何連通性約束基礎上,確保在航路方向上的凸形約束,防止同一次飛行過程中,同一架航空器2次進入相同扇區,增加不必要的協調移交負荷(凸約束可能需要在優化后進一步人工調整)。

2.4流量優化模型

對于給定區域,在上述機場、航路、扇區(點、線、面)三位一體的拓撲結構下,建立開放式流量網絡優化模型,相關參數及符號約定如下:

時隙集T={ti},ti為第i個等分時隙,|T|=NT+1,并假設tNT+1消化前NT個時隙內未分配的流量需求,確保問題具有可行解;

機場集Q={qk},|Q|=NQ;

扇區集S={sj},|S|=NS;

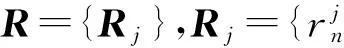
航班集F=Fd∪Fa∪Fc,Fd為區域內出港航班集,Fa為區域內進港航班集,Fc為區域內穿越航班集,|F|=NF;聯程航班對集B={(f,f′)|f,f′∈F},f為前繼航班,f′為后續航班,|B|=NB;

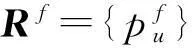
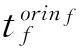
df、af分別為初始計劃的進入和離開區域時隙;

bff′為聯程航班的周轉時間;

Ak(t)、Dk(t)分別為機場qk在t時的進離場容量,二者相互影響,可用凸狀非線性函數曲線表示,如圖3所示；

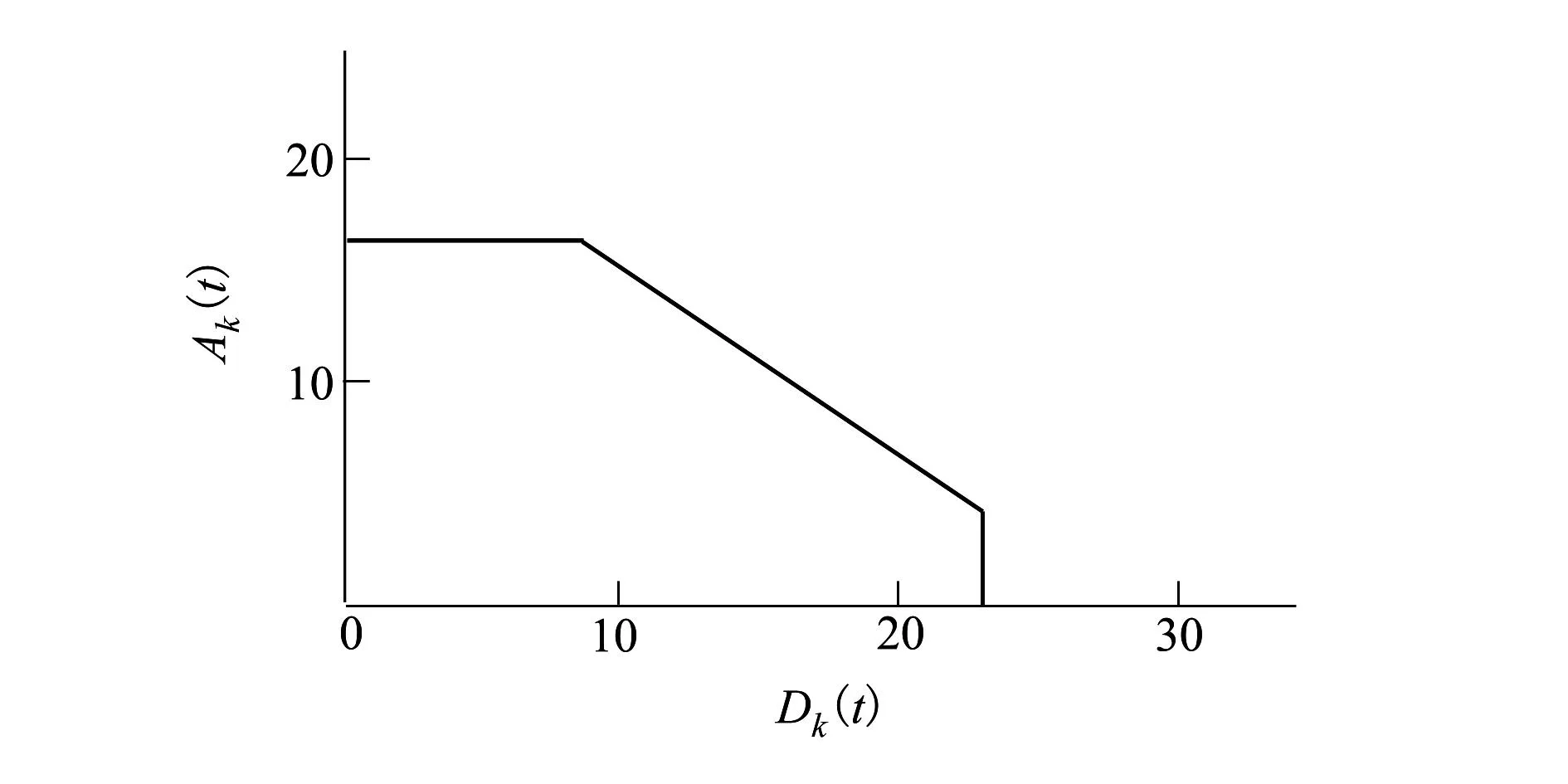
圖3　基于歷史運行數據的機場容量曲線示意圖

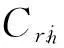
優化區域的總延誤時間分為因本區域容量不足造成的區域內地面等待、空中延誤時間(包括改航造成的飛行延誤和空中盤旋等待時間)和因本區域限流造成的區域外延誤時間(包括向上游區域前推的地面等待和改航造成的飛行延誤時間)2部分,具體包括:Fda內航班的區域內地面等待和空中延誤時間,Fad、Fc內航班的區域外延誤和區域內空中延誤時間,Fd∩a內航班的區域內地面等待和空中延誤時間。

對于f∈Fda∪Fd∩a,區域內地面等待時間為

(12)

對于f∈Fad∪Fc,區域外延誤時間為

(13)

對于f∈Fda∪Fad∪Fd∩a∪Fc,區域內空中延誤時間為

(14)

以總延誤代價最小為目標,則目標函數為

(15)

加入e1、e2表示延誤代價的超線性增長,目標函數將引導延誤均勻分配,避免個別航班延誤超長。例如,選擇2個航班均攤2個時隙的地面等待時間將優于1個航班延誤2個時隙。同時,由于空中延誤代價高于地面等待,令e2>e1。

則目標函數為

(16)

由于飛行流系統區域流控波及效應突出,為減少對上游區域的影響,以本區域造成的區域外延誤代價最小為目標,則目標函數為

(17)

同樣,相對C3以執行區域外地面等待最少為目標,則目標函數為

(18)

約束條件包括

(19)

(20)

(21)

(22)

(23)

(24)

orinf,destf∈A

(25)

sj∈S,orinf,destf

(26)

sj∈S,orinf,destf

(27)

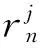
3兩階段求解方法

本文所建立的扇區與流量協同規劃模型具有兩階段、多目標、非線性的特點,適于智能優化算法求解。

3.1基于Voronoi-加權圖的扇區優化遺傳算法

步驟1構造航路網無向圖的Voronoi圖,根據各有限元內航路結構及有限元鄰接關系,按(1)、(2)式計算有限元內權重及相鄰邊權,形成約簡加權圖,并按(3)式確定劃分扇區數m。

步驟2以m為圖的子集數,隨機選取m個有限元的空間目標進行1～m的整數編碼形成m個子集,并將這m個空間目標的鄰元歸入m個子集賦以相同編碼,未被編碼的空間目標歸入相鄰子集,生成初始種群,設定種群規模及終止代數τmax,進化代數τ=0。

步驟3按(8)式取反計算種群個體適應度。

步驟4進行選擇、交叉和變異,并使用精英策略。選擇使用錦標賽方式。交叉算子可能破壞幾何連通性,為此采用文獻[6]中修復策略及基于Hamming距離的交叉選擇。變異算子使負荷最小的子集奪取鄰近負荷最大子集的有限元。

步驟5τ=τ+1,當τ<τmax時,跳轉至步驟3,否則結束。

3.2基于NSGA-II的流量時空優化算法

步驟1預處理以下航班信息:航班編號、航班類別、起飛機場、降落機場、飛行速度、計劃經過扇區與航段、備選改航扇區與航段、計劃進入本區域時間、計劃離開本區域時間、可行進入本區域時間、可行離開本區域時間、MINIT受控航班標志位、MINIT流量控制時間間隔、聯程航班標志位、聯程航班周轉時間。

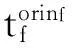
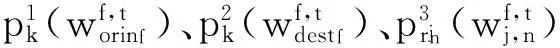
(28)

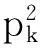
(29)

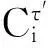
(30)

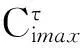
(31)

式中

(32)

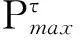
步驟4根據個體序值與同一前端擁擠距離使用錦標賽選擇,然后對f的時隙位基因使用多點交叉和隨機變異算子,生成子種群。

步驟5合并父子種群,重新計算序值與同一前端擁擠距離,通過錦標賽選擇修剪至種群規模。

步驟6τ=τ+1,當τ<τmax時,跳轉至步驟9;否則結束。

4仿真實驗

以北京飛行情報區為例,選取區內13個機場,202個導航臺及報告點,71條航段構成的拓撲網絡和2015年9月某日10:00～12:00區內實際運行的571架次航班為研究對象,應用上述模型算法進行優化求解。在驗證DAC-ATFNOP-(航段容量下降的)ATFNORP-DAC-ATFNOP協同規劃流程框架時,歸并相似環節、簡化實驗步驟,假設在現有靜態扇區拓撲下,受區域內天氣及其他區域限流影響,部分航段通行能力下降,以初始飛行計劃為基礎實施改航操作,然后進行動態扇區生成。

流量優化階段,以Δ=5 min為一個時間片,|T|=25,e1=0.1,e2=0.3,種群大小取400,算法終止代數取500,交叉概率取0.7,變異概率取0.1,分別以C1～C4為主要目標的前端解見表1;

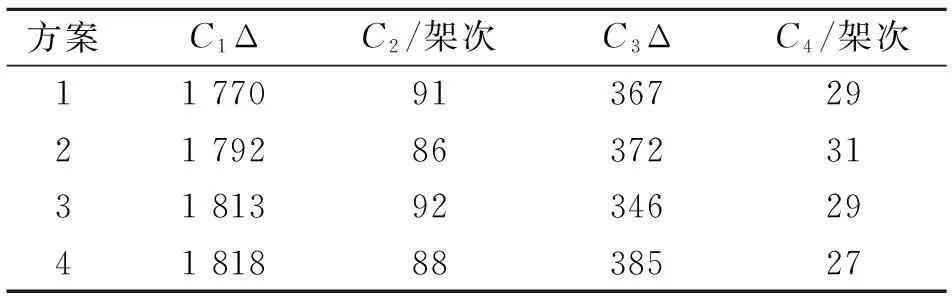
表1　多目標流量優化方案結果

以C1為主要目標,選取方案1進行優化調控。若按先到先服務策略(first come first serve,FCFS),共需調整航班181架次,總延誤代價2 578 Δ。相較FCFS,總延誤時間減少了約31%,執行地面/空中延誤策略減少了約50%。

扇區優化階段,種群大小取200,算法終止代數取200,交叉概率取0.4,變異概率取0.2,Voronoi初始拓撲與最優扇區劃分結果見圖4,扇區優化前后性能指標見表2。

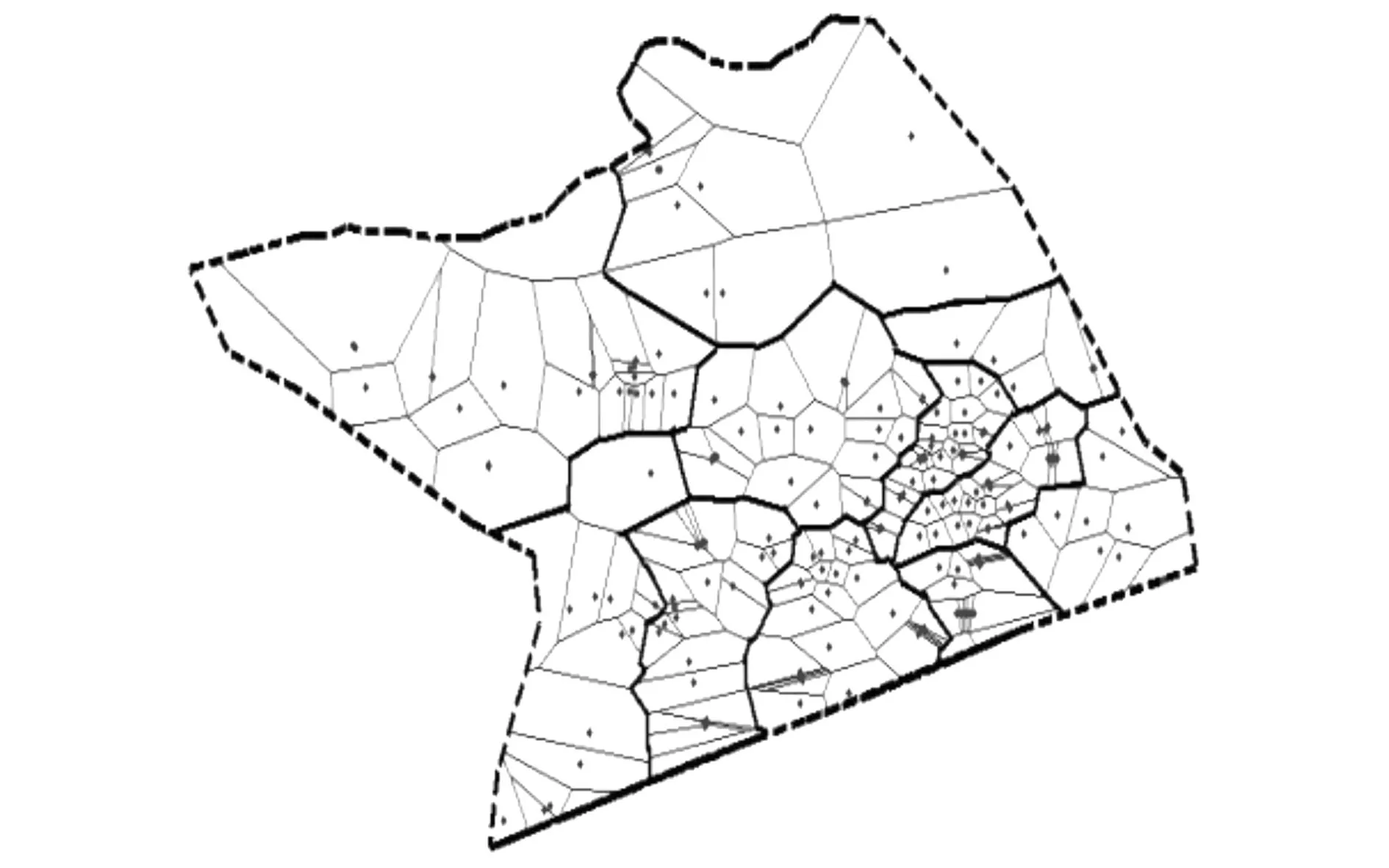
圖4　10:00～12:00最優扇區劃分結果

扇區μ/%σ/(架次·min)ω/%優化前45.0458優化后24.5216 40

表2中引入總負荷平衡系數μ、標準差σ和協調移交負荷減少率ω個性能指標,測度如下

(33)

式中,Wmax、Wmin分別為扇區最大和最小負荷。

(34)

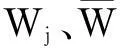
(35)

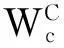
在新扇區拓撲下,按改航后的流量分布進一步調整時隙后,相較在當前扇區拓撲下啟動改航策略,總延誤代價減少了約11%,執行地面/空中延誤策略減少了約20%。綜合兩階段,運行效能得到較大改觀。

5結論

本文旨在為空域與飛行流量協同規劃方法層面探索綜合施策框架提供初步思路,在機場、航路、扇區構成的拓撲結構下,將機場、航路容量及扇區負荷有機整合,并系統考慮區域內外影響,基于扇區動態劃分與流量時空優化,構建了兩階段多目標的協同規劃模型及算法,結合管制區實際運行數據驗證了有效性。從飛行流運行特點和模型本身來看,本文既適用于區域性優化調控,也適用于國家尺度的全局優化。

鑒于研究側重確定條件建模,對惡劣天氣等隨機因素刻畫不足;同時,需考慮高度層劃分,將空域結構與流量調配由2D優化向3D拓展,以便于實際應用;在求解算法的性能改進方面也尚有提升空間。這些也是下一步的研究重點。

參考文獻：

[1]ICAO Doc9854-AN/458. Gloabal Air Traffic Management Operational Concept[S]. Montreal: ICAO, 2005

[2]Yousfi A, Donohue G. Temporal and Spatial Distribution of Airspace Complexity for Air Traffic Controller Workload-Based Sectorization[C]∥Proceedings of the 4thAIAA Aviation Technology, Integration and Operations Conference, 2004: 1-14

[3]Klein A. An Efficient Method for Airspace Analysis and Partitioning Based on Equalized Traffic Mess[C]∥Proceedings of the 6thUSA/Europe Air Traffic Management Research and Development, 2005: 1-10

[4]Delahaye D, Schoenauer M, Alliot J M. Airspace Sectoring by Evolutionary Computation[C]∥Proceedings of the IEEE International Conference on Evolutionary Computation, 1998: 218-223

[5]韓松臣, 張明. 依據管制工作負荷的扇區優化新方法[J]. 南京航空航天大學學報, 2004, 36(1): 91-96

Han Songchen, Zhang Ming. Optimization Method for Sector Partition Based on Control Workload[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2004, 36(1): 91-96 (in Chinese)

[6]Chen Yangzhou, Bi Hong, Zhang Defu, Song Zhuoxi. Dynamic Airspace Sectorization via Improved Genetic Algorithm[J]. J Mod Transport, 2013, 21(2): 117-124

[7]Li Jinhua, Wang Tong, Savai M, Hwang I. Graph-Based Algorithm for Dynamic Airspace Configuration[J]. Journal of guidance, control, and dynamics, 2010, 33(4): 1082-1094

[8]Brinton C, Pledgie S. Airspace Partitioning Using Flight Clustering and Computational Geometry[C]∥Proceedings of the 27thDigital Avionics Systems Conference, 2008: 3-10

[9]Li Jinhua, Seah C E, Hwang I. An Algorithm for Dynamic Airspace Configuration Based on the Air Route Structure[C]∥AIAA Guidance, Navigation, and Control Conference, 2009

[10] Bianco L, Odoni A R. Large-Scale Computation and Information Processing in Air Traffic Control[M]. Berlin, Springer-Verlag, 1993

[11] Vranas P B, Bertsimas D J, Odoni A R. The Multi-Airport Ground-Holding Problem in Air Traffic Control[J]. Operations Research, 1994, 42(2): 249-261

[12] Bertsimas D, Stock S. The Air Traffic Flow Management Problem with Enroute Capacities[J]. Operations Research, 1998, 46: 406-422

[13] Bertsimas D, Stock S. The Traffic Flow Management Rerouting Problem in Air Traffic Control: A Dynamic Network Flow Approach[J]. Transportation Science, 2000, 34(3): 239-255

[14] Bertsimas D, Lulli G, Odoni A R. An Integer Optimization Approach to Large-Scale Air Traffic Flow Management[J]. Operations Research, 2011, 59(1): 211-227

[15] Agustín A, Alonso-Ayuso A, Escudero L F, Pizarro C. On Air Traffic Flow Management with Rerouting. Part Ⅰ: Deterministic Case[J]. European Journal of Operational Research, 2012, 219: 156-166

[16] Dell′Olmo P, Lulli G. A New Hierarchical Architecture for Air Traffic Management: Optimisation of Airway Capacity in a Free Flight Scenario[J]. European Journal of Operational Research, 2003, 144: 179-193

[17] Daniel D, Oussedik S, Stephane P. Airspace Congestion Smoothing by Multi-Objective Genetic Algorithm[C]∥Proceedings of the 2005 ACM Symposium on Applied Computing, Santa Fe, 2005: 907-912

[18] 胡一波. 求解約束優化問題的幾種智能算法[D]. 西安:西安電子科技大學, 2009

Hu Yibo. Several Intelligent Algorithms for Constrained Optimization Problems[D]. Xi′an: Xidian University, 2009 (in Chinese)

Two-Stage Model and Algorithm for Airspace and Traffic Flow Collaborative Programming Based on Dynamic Sectorization

Yao Di1,2, Wang Ying1

1.College of Equipment Management & Safety Engineering, Air Force Engineering University, Xi′an 710051, China 2.State Air Traffic Flow Management Center, Beijing 100094, China

Abstract:Aiming at the coupling interaction of dynamic airspace sectorization and the space-time allocation of air traffic flow, we establish a two-stage collaborative programming model and solution framework to maximize the operational capacity and efficiency. The first stage begins with the construction of a Voronoi cells based weighted graph model combined with Voronoi diagram and graph theory for the topological structure of given airspace and air traffic distribution. Then, the sector re-partitioning problem is solved based on genetic algorithm to balance the sector workloads and minimize the coordination workloads. In the second stage, we built air traffic flow network optimization model to reduce the total delay fairly, the ground delay out of the area fairly, the total number of delayed fights and the number of ground-delayed fights out of the area, with the airspace capacity constraint in the area and the minutes-in-trail restriction out of the area. Then, the multi-objective optimization problem is solved based on the non-dominated sorting genetic algorithm II (NSGA-II) for a combination of flow management actions, including ground holding, airborne holding, and rerouting. We explore the comprehensive framework for alleviating the traffic congestion according to the priority order of strategies described above. Simulation results show that: the proposed model can provide supporting decision-making for improving the operational quality of air traffic management.

Keywords:air traffic management; air traffic flow management; airspace management; algorithms; computer simulation; decision making; dynamic airspace configuration; dynamic airspace sectorization; efficiency; genetic algorithms; mathematical models; NSGA II (non-dominated sorting genetic algorithm II); optimization; topology; two-stage collaborative programming; Voronoi cells; Voronoi diagram

收稿日期：2015-12-01

基金項目：國家自然科學基金(71171199)與國家空管“十二五”科研專項課題(GKG201401003)資助

作者簡介：姚頔(1984—)，空軍工程大學博士研究生，主要從事信息系統工程與智能決策、空域與飛行流量管理的研究。

中圖分類號：V355.1

文獻標志碼：A

文章編號:1000-2758(2016)04-0549-09