滾動軸承振動性能因素分析的定性融合理論

徐永智，夏新濤

(1.西北工業大學 機電學院，西安 710072；2. 河南科技大學 機電工程學院，河南 洛陽 471003)

滾動軸承的制造安裝因素直接影響其運行過程中的動態特性、使用壽命和可靠性，其中多體現在軸承振動方面，其測量及結果分析受到行業的普遍關注[1]；軸承振動信號數據采用時域特征、神經網絡法以及光譜分析處理[2-4]來分析軸承故障診斷以及故障處理；文獻[5-6]分析了軸承的振動特性及特征參數；文獻[7-12]研究了振動與噪聲的相關性以及減振降噪的方法措施。以上研究從不同方面揭示了軸承振動的特征，為軸承性能的進一步研究提供了很好的經驗，但很少涉及軸承振動影響因素的定性分析。

鑒于此，現提出一種軸承振動性能影響因素分析的乏信息定性融合理論。

1 定性融合理論

定性融合理論：信息系統有很多特征，揭示信息系統特征的方法眾多，利用每種方法可揭示信息系統某個側面的信息特征，從而獲得信息系統的特征信息集，對特征信息集進行融合做出合理的決策，最終推斷總體特征信息。

1.1 定性融合

定性融合是指在給定的論域U中，已知解集

F=(f1,f2,…,fj,…,fh)；j=1,2，…，h，

(1)

fj=(fj1,fj2,…，fjn)，

式中：j為方法；h為方法個數。記“屬性一致性于”為符號“?”，在解集F中，總存在且至少存在一個來自F的元素集合，是滿足準則Θ的最終解f0，表示為

f0|Θ|FromF?F0，

(2)

式中：F0為系統屬性的真值集合即白箱問題；|Θ表示在準則Θ下；|FromF表示來自F的元素。

由于系統信息的復雜多樣性，用不同數學方法進行分析會得出不同結果fj，甚至有些結果可能是相互矛盾的。若將這些結果看成是一個個解的集合即解集F，則定性融合是指在某種準則下，從F中提取具有某種一致性元素的子集，并將該子集作為系統的最終解f0。

定性融合有兩方面的含義：一是融合，即考慮各個解集；二是定性，即不再進行復雜的數學計算，只是尋求某種一致性，而且最終解中的元素全部來自解集F，沒有出現更新的信息。

2 定性融合理論的應用

以圓錐滾子軸承振動加速度為例，基于灰色系統理論[13-14]，提出軸承性能影響因素的灰色定性融合分析方法。

影響圓錐滾子軸承振動加速度的因素中，主要考慮套圈和滾子的加工質量參數。加工質量參數很多，必須針對其中的主要因素才能有效地控制軸承振動加速度值。另外，考慮試驗成本，生產現場抽樣個數較少。在有限的數據個數條件下尋找出最重要的因素是關鍵問題。

根據軸承乏信息試驗分析與評估原理，比較可靠的措施是運用多種數學方法得出多種結論，由于每種結果都有其局限性，因此應對這些結果進行對比分析和融合，得出具有共性的一個結論，該結論就是影響圓錐滾子軸承振動加速度的最重要因素，即問題的最終解。

2.1 軸承性能影響因素分析的定性融合模型

設已知有N個相互獨立的因素(如結構參數和潤滑條件等)可能會影響軸承的性能(如振動)P，因素符號集為

X=(X1,X2,…，Xi,…，XN)；i=1,2，…，N,

(3)

式中：i為影響因素。

用m種數學方法對試驗數據進行處理，得到N個影響因素排序集(因素的影響從大到小排序，對性能影響越大的因素，其符號位置越靠左)，即對于性能P，有

(4)

可得到排序因素符號矩陣為

(5)

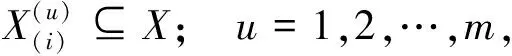
式中：?表示優于；u為用第u種數學方法。

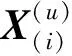
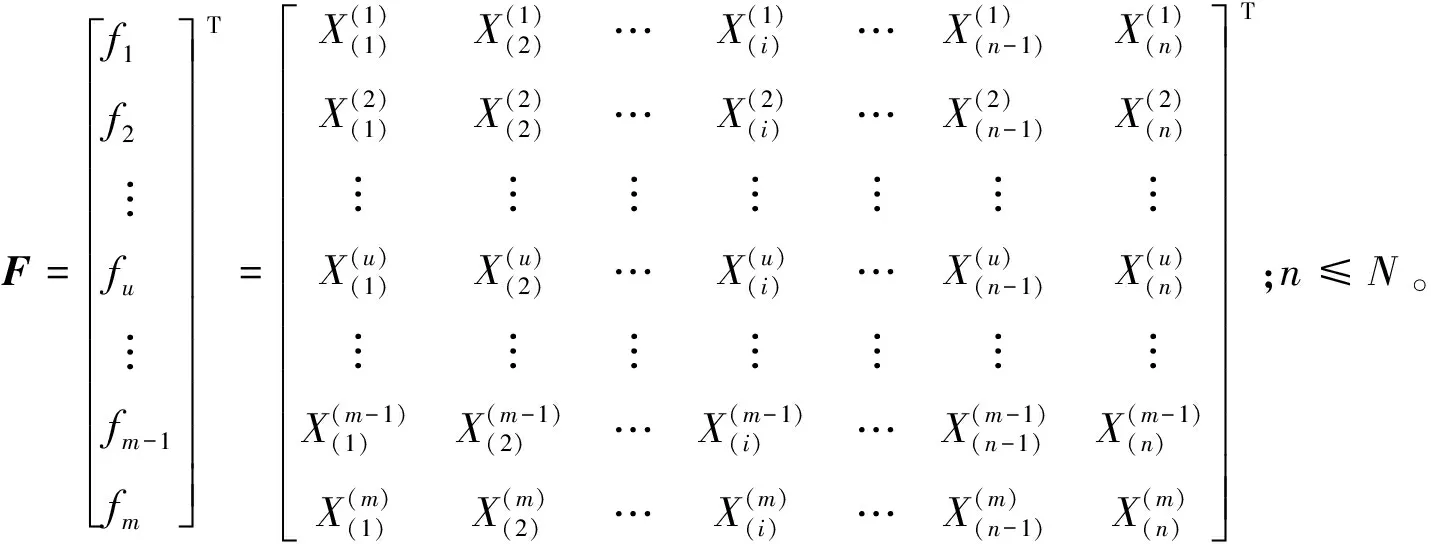
(6)

則最終解f0為F中均具有的因素的集合(符號)，即

(7)

若基數f0≠Φ(Φ為非空集合)，則定性融合有唯一解。

在最終解f0中，s個因素是不分前后順序的，均為影響軸承性能P的主要因素，將其改用新的符號并重新編號，有

f0=(x1,x2,…,xi,…,xs)?X;1≤s≤n，

(8)

一般n∈[0.5N,N]。由此可以看出在f0中沒有新信息。

2.2 解集獲取方法

設軸承振動加速度值X0構成的數據序列為

X0=(x0(1),x0(2),…,x0(k),…,x0(K))；

k=1，…,2…,K，

(9)

式中：K為數據個數。

影響因素Xi構成的數據序列為

Xi=(xi(1),xi(2),…,xi(k),…,xi(K))。

(10)

2.2.1 灰色關聯度方法

1)均值化變換

軸承振動均值化比較數列為

(11)

軸承振動均值化參考數列為

(12)

2)求在各點上X0與Xi的關聯系數L0i(k)

(13)

Δ0i=|y0(k)-yi(k)| ，

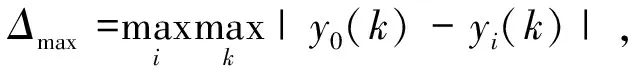
式中：ξ為分辨系數，ξ∈(0,1)。

3)求關聯度

(14)

4)排關聯序

將m個子序列對同一母序列的關聯度按序排列，組成關聯序，其直接反映各個子序列對同一母序列的“優劣”或“主次”關系。若γ0a﹥γ0b，則稱子序列Xa對于相同母序列X0有優于子序列Xb的特點。

2.2.2 灰色絕對關聯度方法

設序列X0與Xi的長度相同且初值均不為零，則可用灰色絕對關聯度來表征X0與Xi的相對始點的幾何形狀之間的關系，若X0與Xi的幾何形狀越接近，其絕對關聯度越大。灰色絕對關聯度計算步驟如下：

1)初值零化處理

軸承振動零值初化的參考數列為

y0(k)=x0(k)-x0(1) ，

(15)

軸承振動零值初化的比較數列為

yi(k)=xi(k)-xi(1) 。

(16)

2)計算絕對關聯度

(17)

其中，軸承振動斜率參考數列為

軸承振動斜率比較數列為

灰色絕對關聯度ε0i具有以下性質：

1) 0<ε0i≤1；ε0i恒不為零，表明任何2個序列都不是絕對無關的；

2)ε0i只與Xi和X0的幾何形狀有關，而與其相對位置無關，即平移不會改變絕對關聯度的值；

3)ε0i越小，Xi和X0的相似程度越小，聯系越不密切；

4)ε0i越大，Xi和X0的相似程度越大，聯系越密切；

5)ε0i=1，表明Xi和X0完全相同，無任何區別。

2.2.3 灰色相對關聯度方法

1)計算初值像

軸承振動初值像參考數列為

y0(k)=x0(k)/x0(1)，

(18)

軸承振動初值像比較數列為

yi(k)=xi(k)/xi(1) 。

(19)

2)求始點零化像

軸承振動零值初化的參考數列為

z0(k)=y0(k)-y0(1)，

(20)

軸承振動零值初化的比較數列為

zi(k)=yi(k)-yi(1)。

(21)

3)計算灰色相對關聯度

(22)

其中，軸承振動斜率參考數列為

軸承振動斜率比較數列為

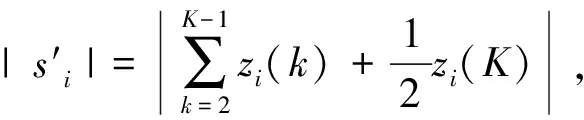
灰色相對關聯度γ0i具有以下性質：

1) 0<γ0i≤1；γ0i恒不為零，表明任何2個序列都不是絕對無關的；

2)γ0i可以表示Xi和X0相對初始點的變化速率之間的關系，Xi和X0的變化速率越接近，γ0i就越大，反之就越小；

3)γ0i=1，表明Xi和X0完全相同，無任何區別。

2.3 應用實例

以30204型圓錐滾子軸承的振動加速度問題為例，通過試驗來研究軸承套圈和滾子的參數與軸承振動之間的關系，以尋求控制軸承振動質量的乏信息方法。

以30204軸承的16個套圈參數和16個滾子參數作為研究對象。質量參數共32個，其中宏觀誤差參數21個，微觀誤差參數7個，其他4個；滾子質量參數16個，內圈質量參數9個，外圈質量參數7個，通過試驗研究軸承各項參數與振動之間的關系。

試驗所用符號及其含義見表1。其中，“均”代表一套軸承中15個滾子該項參數的均值；“差”代表一套軸承中15個滾子該項參數的極差。

表1 滾動軸承符號

軸承振動加速度X0的測量結果為

46.0，47.7，47.7， 47.0，48.0，47.7，48.0，47.7，47.7，46.7，47.7 ，44.0，46.0，46.7，48.0，45.0，47.0，45.3，45.7，45.3，47.3，48.0 ，47.0，47.3 ，47.3，47.0，47.3，46.7，44.6，47.3 dB。參數X1～X32的試驗數據見表2～表5。

表2 滾子測量數據(均)

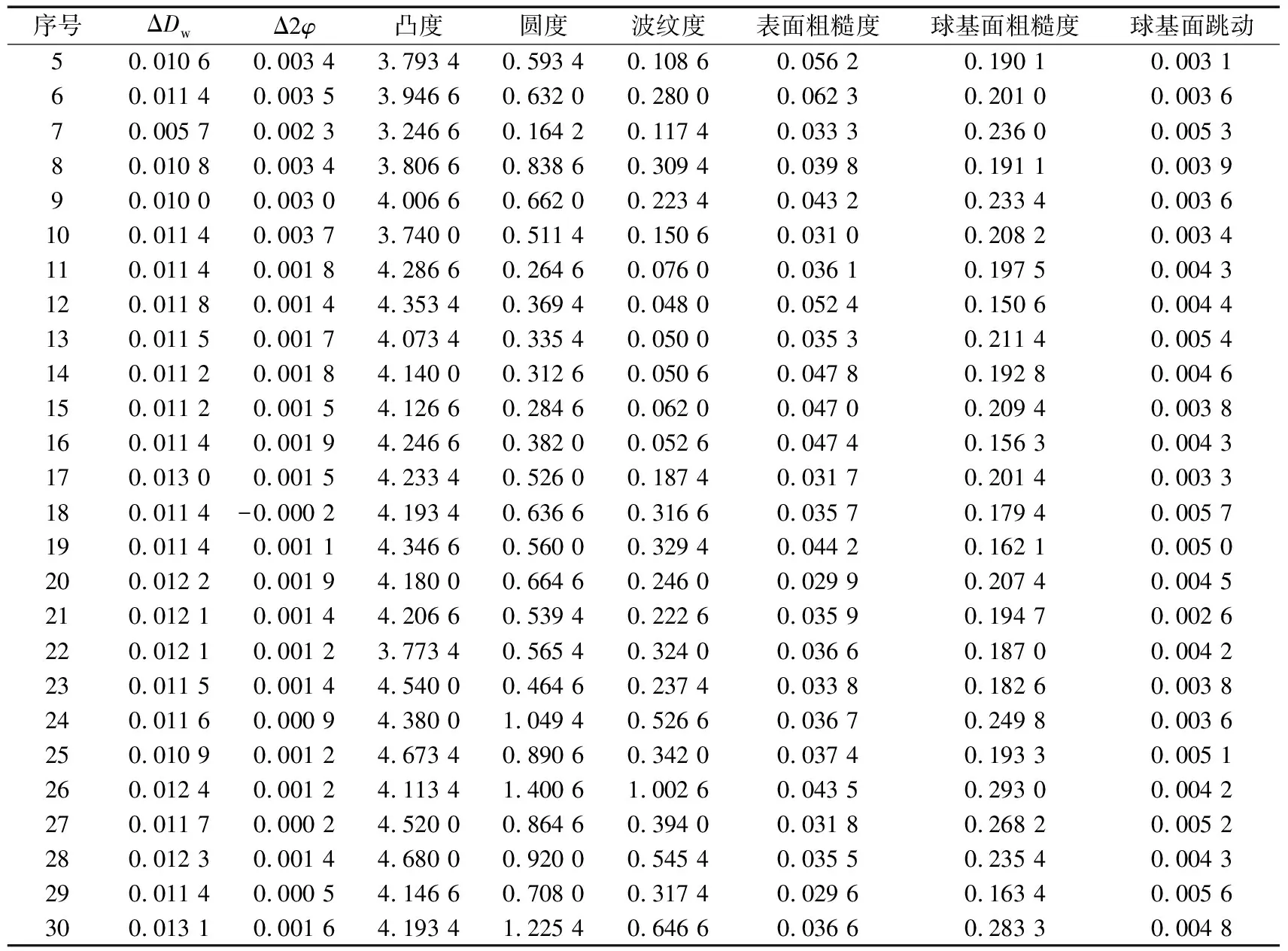
續表 μm

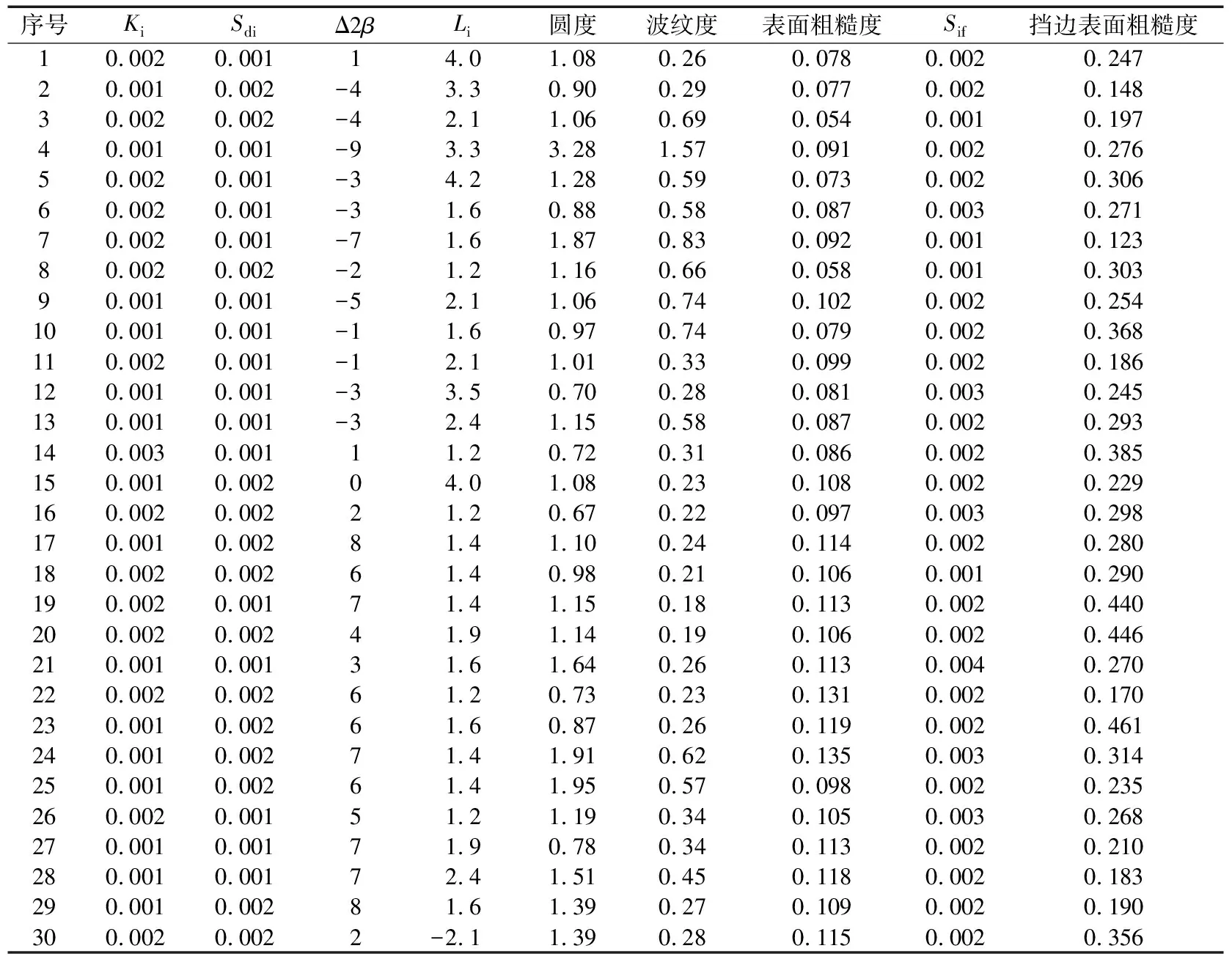
表4 內圈測量數據

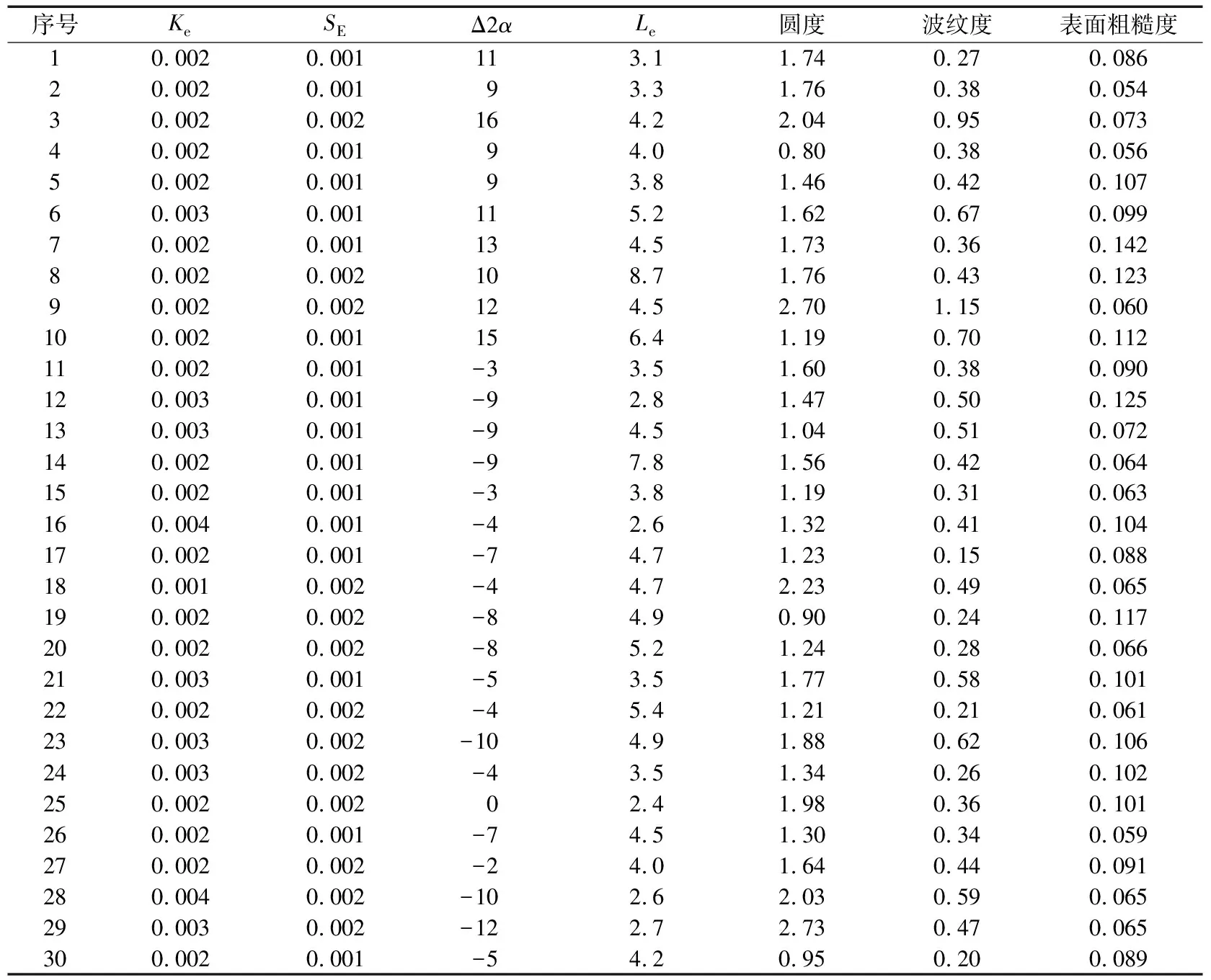
表5 外圈測量數據

根據灰色關聯度法(ξ=0.5)、灰色絕對關聯度法、灰色相對關聯度法，得到各參數與振動的關聯度、絕對關聯度、相對關聯度，結果見表6(按照從小到大的順序排列)。

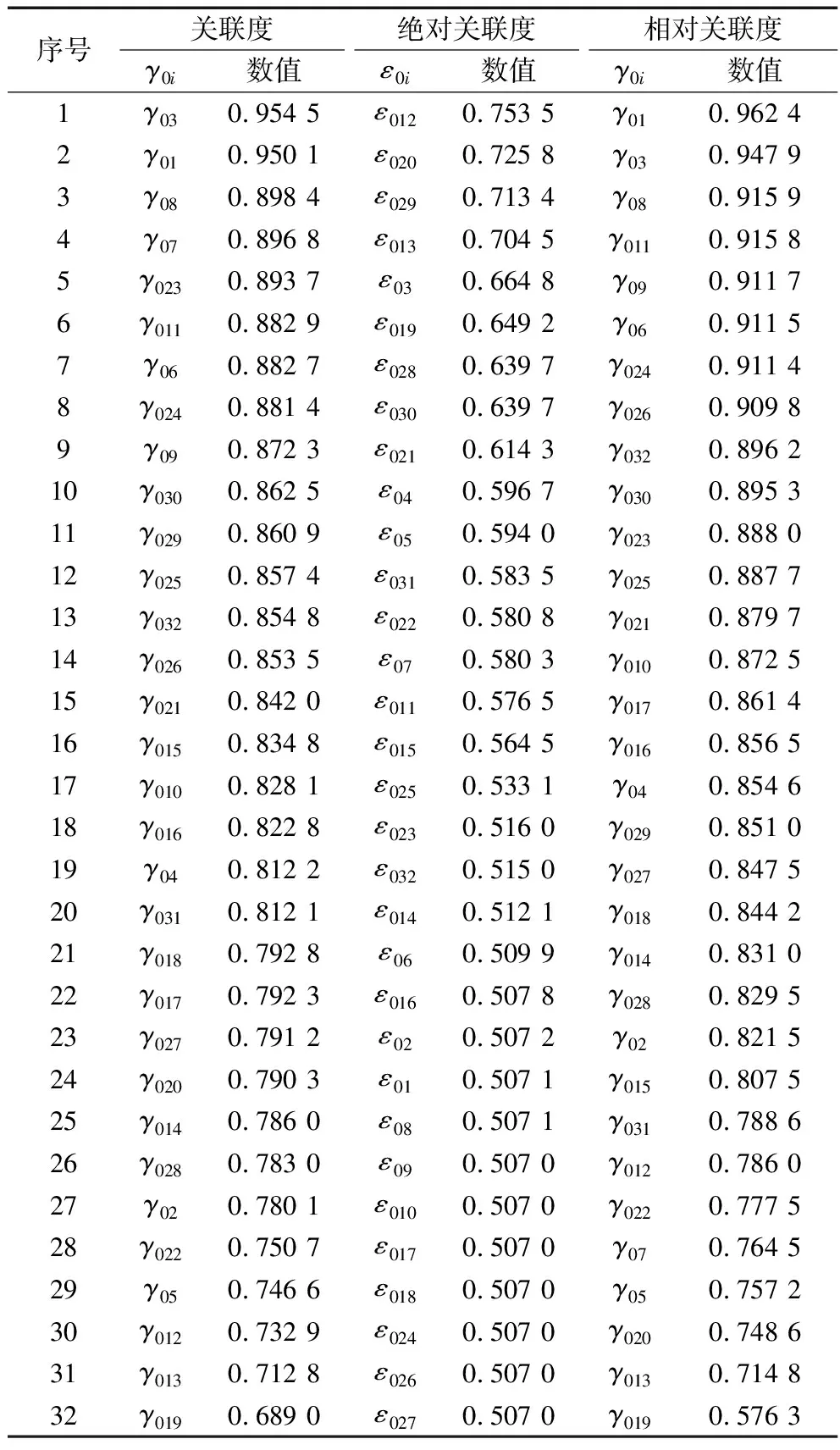
表6 軸承參數與振動的關聯度

將以上3種方法排序結果中前16名取出，用因素符號Xi列于表7。由表可知，最重要的因素集合為f0=(X3,X11,X21,X30)。

表7 3種方法計算結果的前16名因素

在3種數學方法的排序結果中，將前16名因素作為可能的重要因素，其出現的頻數和影響程度分別見表8、表9，將表8中的影響因素進行分類，結果見表10。

表8 影響因素在3種計算結果中出現的頻數

表9 3種方法中各因素的影響程度

表10 主要影響因素的誤差類型

由表9、表10可知，共有28個主要因素，其中滾子質量參數14個，內圈質量參數8個，外圈質量參數6個。因此，試驗軸承零件對振動加速度的影響權重比為滾子/內圈/外圈=14/8/6≈2.3/1.3/1。

從最重要因素和第2重要因素中發現，共有16個主要因素，其中滾子質量參數8個，內圈質量參數4個，外圈質量參數4個。因此，試驗軸承零件對振動加速度的影響權重比為滾子/內圈/外圈=8//4/4=2/1/1。

從最重要因素中發現，共有4個主要因素，其中滾子質量參數2個，內圈質量參數1個，外圈質量參數1個。因此，試驗軸承零件對振動加速度的影響權重比為滾子/內圈/外圈=2/1/1。

綜上所述，在測量條件下，對試驗軸承振動加速度貢獻最大的是滾子，其次是內圈和外圈。主要原因是滾子質量參數最多，內圈次之，外圈最少。

試驗發現，對滾子而言，圓錐表面素線凸度是試驗軸承的最薄弱環節。說明凸度的形狀、大小及加工質量對軸承振動加速度有重要影響；對套圈而言，滾道圓度誤差是試驗軸承的最薄弱環節。以上4個質量參數均為宏觀誤差參數。

理論上，在使用過程中，圓錐滾子軸承滾子的2條素線、中心線以及軸承中心線相交于一點時，軸承的振動最小；然而，在軸承設計時應考慮應用載荷的影響。當應用載荷等于設計載荷時，滾子的2條素線、中心線以及軸承中心線相交于一點，軸承振動較小；但實際應用中應用載荷和設計載荷并不相等，滾子凸度受載時，滾子的2條素線、中心線以及軸承中心線并不相交于一點，滾子與套圈接觸的直線長度發生變化而產生振動，可見，滾子凸度影響軸承的振動。應用載荷和設計載荷相差越大，其影響程度就越大；而同類因素的直線度則受載荷影響較小，對振動影響較小。本試驗中試驗載荷和設計載荷不相等，滾子凸度是影響軸承振動的最大因素，因此與波紋度、圓度、表面粗糙度是最大影響因素的結論有所出入。

3 結束語

定性融合性分析方法是軸承及其他機械產品性能研究的發展方向。其意義在于：一是從經濟學角度，能夠從少量試驗中得到大量信息，做出合理的評估、預測，可以大大降低成本；二是從信息量的角度，能夠利用一些數學工具及理論融合，在相同試驗數據中挖掘出大量信息，大大提高資源的利用效率。

融合性分析方法也有缺點和許多需要完善之處，如融合性分析方法的范圍，上述只是其中一部分方法的融合，還有許多其他方法有待挖掘、完善；融合性分析方法對適用對象有要求，要根據其特點選擇不同方法融合；在融合性分析方法使用過程中參數的確定也有待進一步研究。