差分振子在滾動軸承故障診斷中的應用

劉燕，胡學青,劉浩，張明玉

(宿州學院 煤礦機械與電子工程研究中心，安徽 宿州 234002)

滾動軸承發生故障時，其振動信號往往呈現出強烈的非平穩性及非線性特征，軸承早期故障信號的特征相對微弱，容易淹沒在其他振動信號和隨機噪聲中，采用傳統的時頻分析方法[1-3]很難從混有強背景噪聲的振動信號中提取微弱故障信息。混沌振子法[4-6]和隨機共振法[7-9]已經廣泛應用于微弱信號的檢測中。差分振子法[10]的運算代碼為加減運算，速度快，更適合對運算速度要求較高的場合；而且不受檢測信號相位的影響，檢測結果更加準確。另外，差分振子有一定的容錯特性，可在一定程度上消除加工誤差導致的計算頻率偏差；而且不用過濾噪聲，噪聲只會使相圖周圍變得粗糙，并不影響整個系統的穩定性。

目前，關于差分振子的研究較少，文獻[11]將差分振子方法應用于同步發電機轉子匝間短路及轉子碰摩故障的識別中，取得了良好的效果；文獻[12]將差分振子方法軸承故障和齒輪故障的早期數據進行了分析，成功地提取出了故障早期的微弱特征。在此，將差分振子方法應用于滾動軸承故障診斷中，基于其檢測帶寬特性和幅值檢測特性實現軸承的早期故障檢測。

1 差分振子檢測器的構造

差分振子檢測器是以二元差分方程為基礎構造的檢測器[11]，具體數學模型如下

(1)

令α=-(a+d)，β=ad-bc，f(k)=bp·

cos(2kπfe+2kπfd/fs) ，則(1)式可簡化為

xk+2+αxk+1+βxk=f(k)T(k) ,

(2)

式中：a,b,c,d為差分振子的系統參數；p為放大倍數(一般取整數，1，2，4，8)；fe為系統激勵頻率；fd為待檢測頻率；fs為輸入信號的采樣頻率；T(k)為輸入信號。

2 差分振子參數設置原則

差分振子設置原則如圖1所示：首先，確定差分振子系統參數，通過仿真確定最合適的系統參數；其次，確定系統激勵頻率fe，用差分振子檢測信號，必須使系統激勵頻率等于系統固有頻率，即f0=fe(f0=ω0/2π ，ω0=arccos[-α(1+β)/4β] )，否則不能檢測信號；然后，確定檢測頻率fd，若被測信號中含有fd這一頻率成分, 則系統產生共振, 噪聲得到抑制，不需要濾噪，其相圖隨即發生變化;最后，通過觀察系統的相圖變化判斷系統是否含有待檢測頻率，從而可以實現早期故障的檢測。

當向差分振子系統中輸入待檢測信號后，若差分振子相圖收斂于極環，則信號中含有待檢測頻率信號；反之，如果收斂于極點，則可能檢測信號中本來就不存在待檢測頻率信號，或者是待檢信號中噪聲信號強度過大，導致信噪比過低，無法檢測出待檢測頻率信號。

3 差分振子特性

3.1 檢測帶寬特性

構造仿真函數

T(k)=0.1sin(2kπ×17)+g·randn(k) 。

(3)

在檢測過程中，將檢測頻率設置成以17 Hz為中心的一系列取值，對輸入信號中的17 Hz的頻率成分進行檢測。差分振子參數設置為：α=0.97；β=0.97；fe=0.331 9 Hz；x0=8；y0=8;fs=1 000,p=1,g=0.1(隨機噪聲方差)。從圖2可以看出，當檢測頻率為18 Hz時，相圖也收斂于極環，說明待檢測信號中含有17 Hz的頻率成分，此時最大檢測帶寬為1 Hz，在工程應用中是允許的。

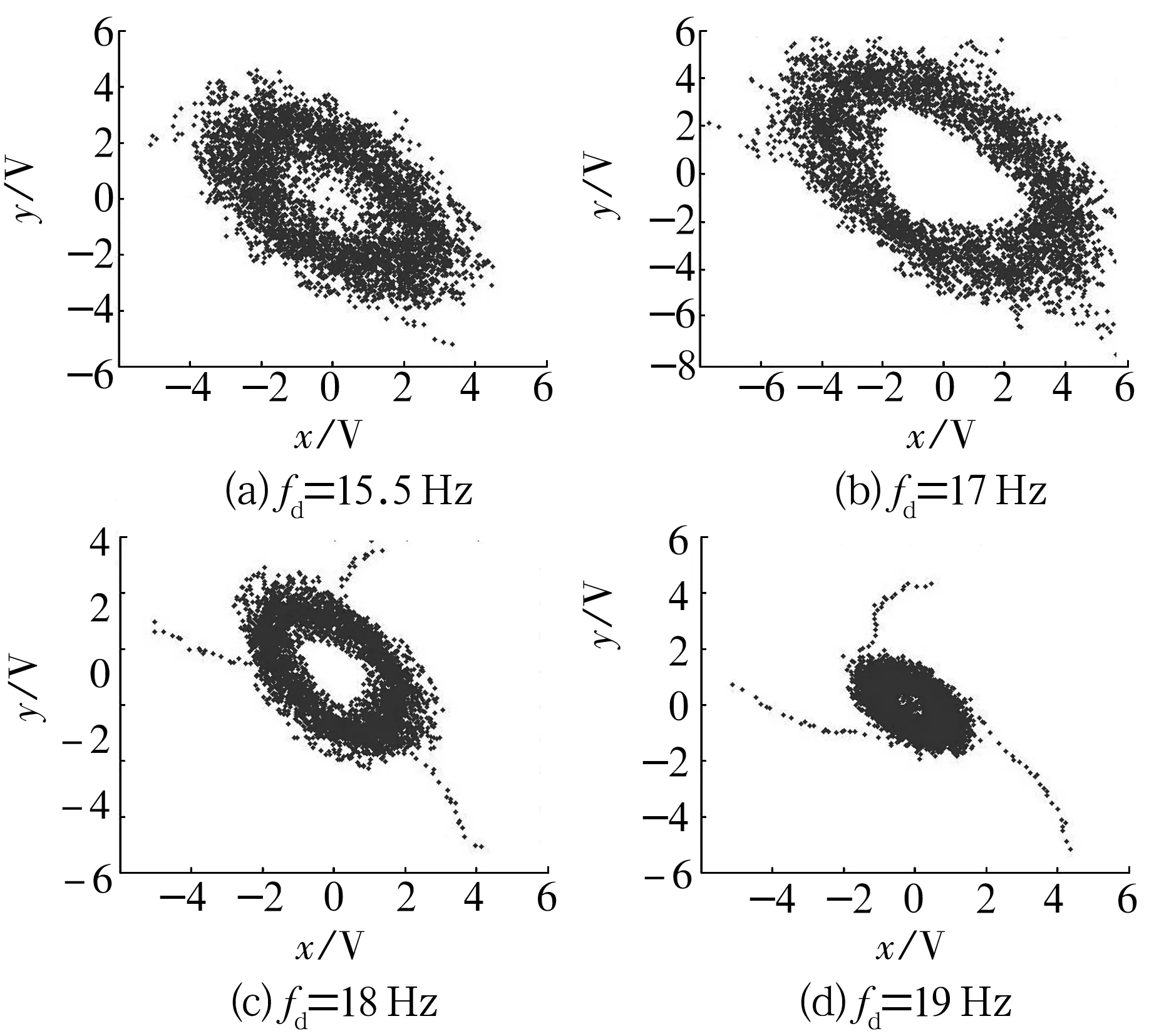
圖2 不同檢測頻率下的差分振子相圖

仿真表明：差分振子的檢測頻率有一個波動范圍，以檢測頻率為中心，以B=2b/fs為帶寬的頻率均敏感，即差分振子檢測有一定的檢測帶寬。帶寬的大小與α和β的取值有很大的關系，其中β的取值越大，差分振子的容錯性能越差，檢測帶寬越寬。在工程實際中，由于考慮到各種誤差的存在，一般不將α和β值取得很大，通常更加注重差分振子的容錯性能。

3.2 幅值檢測特性

在工程實際中，信號頻率的提取很重要，而信號幅值的檢測依然是一個難題。

設待檢測信號為

s(t)=Acos(2πt×50)+0.2randn(1,t) ，

(4)

式中：A為信號幅值。

差分振子參數設置為：a=0.03,b=1.0,c=-1,d=-1,x1=5,y1=5,fe=0.331 9,fd=50,fs=1 000,p=1。則不同信號幅值下的差分振子相圖如圖3所示。

從圖3可以看出，噪聲強度相同時，相圖的大小與幅值有著很緊密的關系，幅值越大，相圖越大，相圖的變化與幅值的增加呈線性比例關系。為了證明此結論，給定輸入信號D(k)，設對應差分方程的解為ck，代入差分方程得

ck+2+αck+1+βck=f(k)D(k) 。

(5)

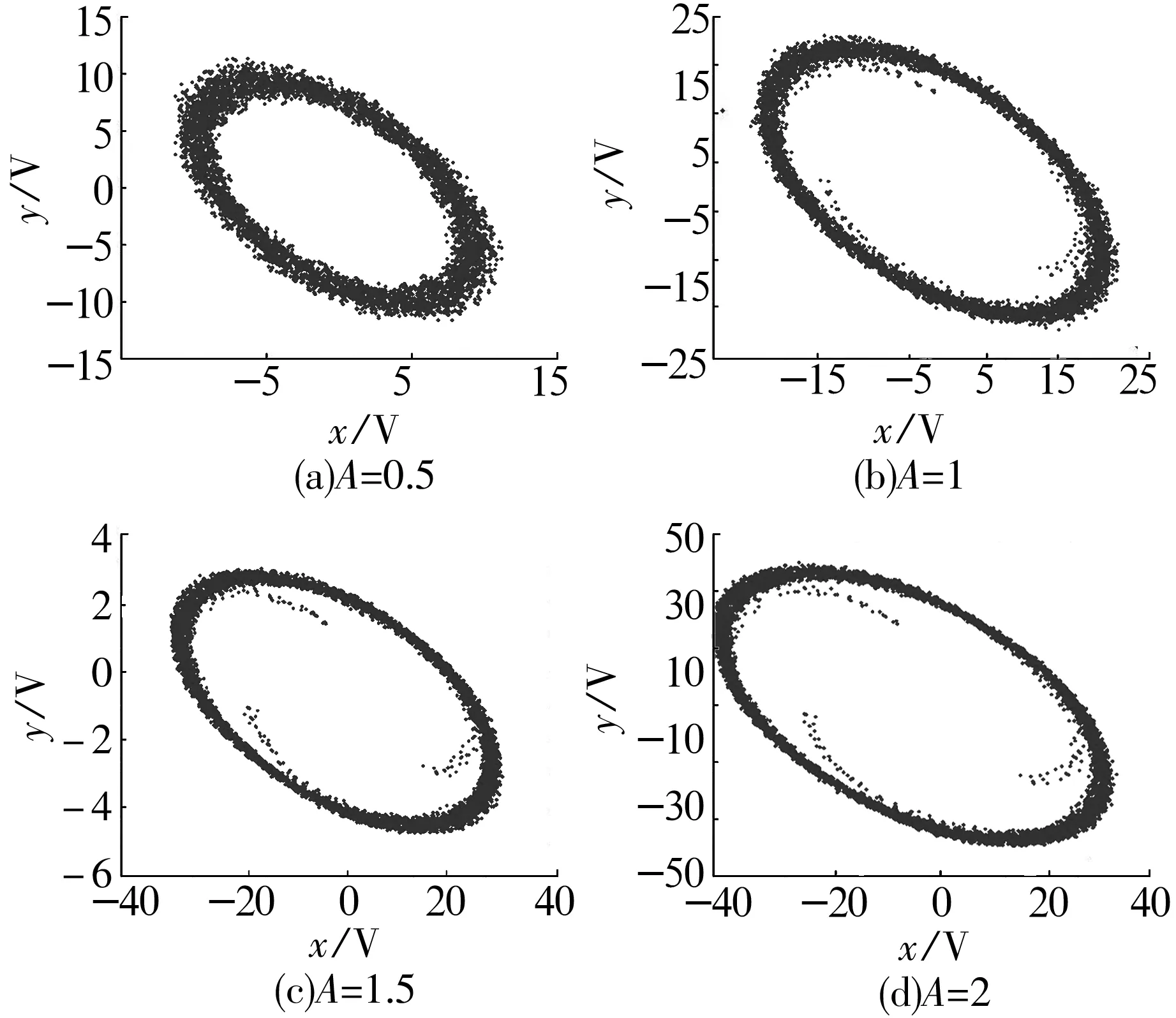
圖3 不同信號幅值下的差分振子相圖

如果輸入信號的幅值增大到原來的k倍，即S(k)=kD(k)。假設S(k)對應方程的解為yk，則

yk+2+αyk+1+βyk=f(k)S(k)。

(6)

將(5)式兩邊同乘以k得

kck+2+α(kck+1)+β(kck)=kf(k)D(k)。

(7)

對比(6)式和(7)式可知

yk+2=kck+2，

(8)

可見輸入信號的幅值增大k倍，差分振子方程的解也增大了k倍，則相應的差分振子相圖也擴大了k倍。所以呈單調遞增的線性關系。此結論為可視化檢測故障提供一定的依據。

4 工程應用實例

試驗軸承型號為30210型圓錐滾子軸承，采用SG雙色金屬刻字機模擬滾子早期點蝕故障，故障直徑約0.3和0.5 mm，深度約幾十微米。選用BVT-5軸承振動測量儀，徑向與軸向加載力分別為150和120 N，采樣頻率為5 120 Hz，主軸轉速為1 800 r/min。根據軸承參數計算得滾子故障特征頻率為103.16 Hz。使用加速度采集儀采集故障信號并導入MATLAB，其時域波形如圖4所示，經FFT處理后得到的頻譜圖如圖5所示。

從圖4中完全看不出故障特征頻率，而在圖5中也無法精確找到對應的滾子故障特征頻率，特征頻率完全被噪聲所淹沒。因此，依靠傳統的時頻方法無法準確判斷軸承故障。

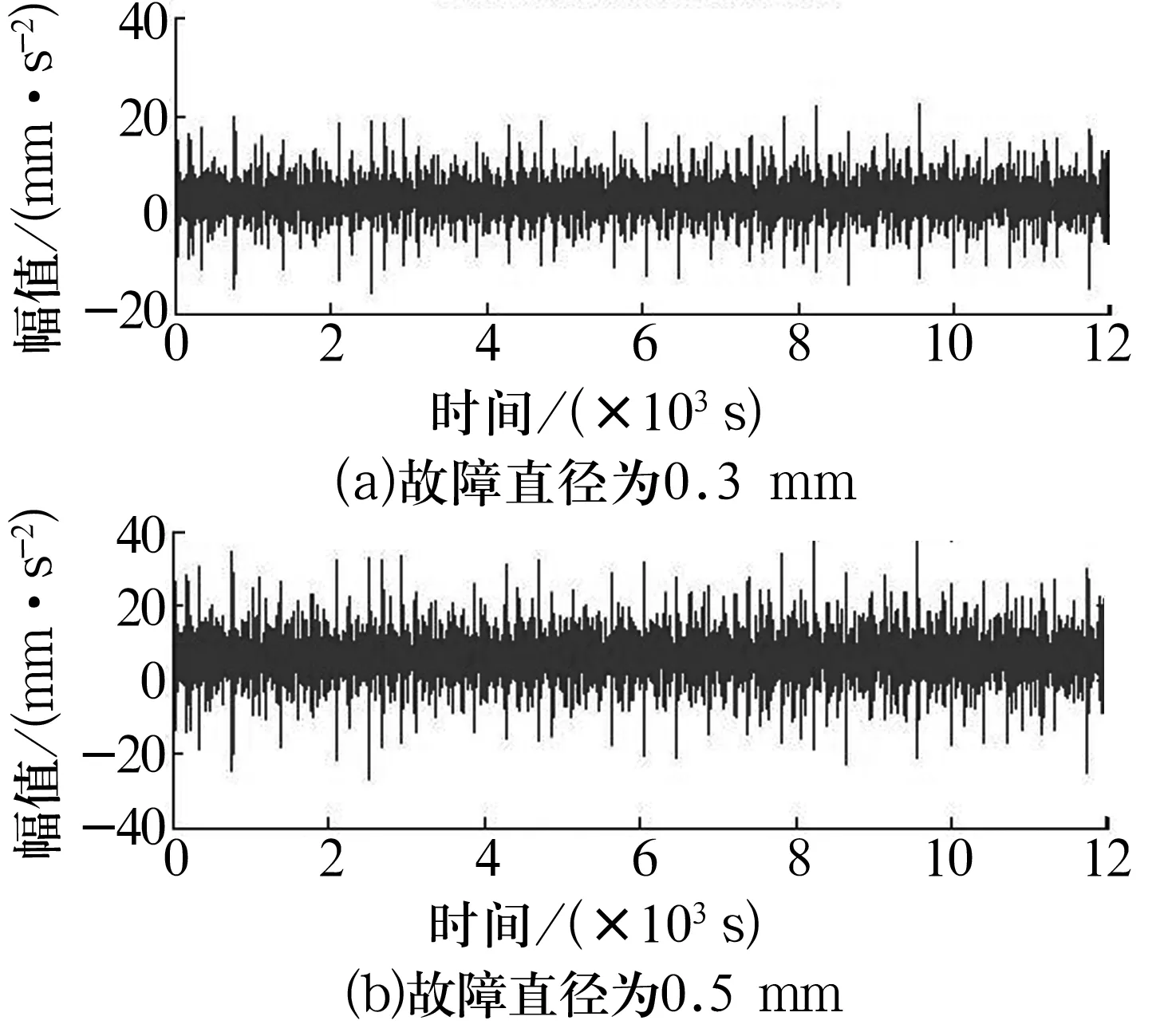
圖4 信號的時域波形

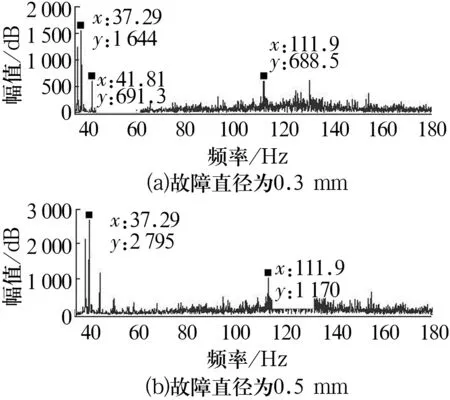
圖5 信號的幅值譜

令α=0.97，β=0.999，fe=0.330 6 Hz，p=2。當fd=103.16 Hz時，得到的差分振子相圖如圖6所示。從圖中可以看出，故障直徑為0.3 mm的差分振子相圖收斂的極環面積明顯小于故障直徑為0.5 mm的差分振子相圖，隨著故障直徑的增大，滾子損傷的區域越來越大，故障有惡化的趨勢。說明差分振子不但可以檢測信號的頻域信息，也可以直觀觀察信號的幅值信息。

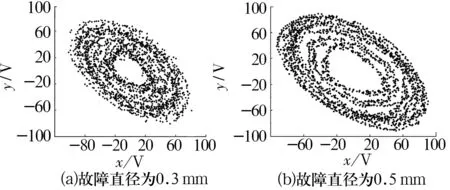
圖6 信號的差分振子相圖

5 結束語

差分振子法可通過連續觀察相圖大小的變化，從而發現故障信號幅值的變化，在線觀察故障變化趨勢。但檢測微弱信號時涉及參數很多，且每個參數的取值均由仿真得來，尚無理論推導，目前關于差分振子的研究工作還處于初期階段，有待進一步研究。