考慮底板變形修正的錨桿抗浮設計方法

葉　蓁，唐　浩

(浙江綠城六和建筑設計有限公司，浙江 杭州 310013)

?

考慮底板變形修正的錨桿抗浮設計方法

葉蓁，唐浩

(浙江綠城六和建筑設計有限公司，浙江 杭州 310013)

摘要：現有錨桿抗浮計算無法考慮錨桿、基礎和上部結構的剛度及基礎底板變形對錨桿受力不均勻性的影響。在此，探討錨桿抗浮的不同計算方法，并引入變形修正因子對現有設計結果進行修正。計算結果表明，考慮底板變形修正后的錨桿所受的拉力相比于現有設計方法計算的錨桿拉力更加準確，對實際工程具有一定的參考價值。

關鍵詞：錨桿；抗浮；底板變形

抗浮錨桿能夠很好地抵抗浮力，對控制結構整體或局部上浮、底板變形和開裂都有很好的效果。但是，由于錨桿、基礎與上部結構是相互作用的，且結構的荷載和變形比較復雜，對于帶有大面積地下室或塔樓偏置的結構，常用錨桿設計方法所基于的假定與實際情況有較大偏差，不能反映結構的實際受力和變形情況。因此，現有均勻布置抗浮錨桿的方式無法有效、經濟地設置錨桿。鑒于此，有必要對抗浮錨桿的計算方法進行改進，以便為今后應用錨桿來處理地下室抗浮問題提供科學依據和理論指導，而且對促進抗浮錨桿的工程設計、減小現場試驗的耗費、完善抗浮錨桿的研究也具有積極的意義。

1抗浮錨桿的設計方法

1.1常規(guī)設計法

常規(guī)錨桿設計方法是將地下水浮力作為可變荷載施加于地下室底板底面，將地下室自重作為永久荷載，于是抗浮錨桿所受荷載的設計值按最不利荷載的組合確定為

qd=(γQqwkS-γGgk)/S

(1)

則單根錨桿的軸向拉力設計值Nt為

Nt=qdSxSy

(2)

式中：qwk為水浮力標準值；

Gk為結構及覆土自重標準值之和；

γQ為可變荷載分項系數；

γG為永久荷載分項系數[1]；

Sx、Sy分別為錨桿的縱向和橫向間距；

S為底板標準柱跨的面積。

常規(guī)設計方法的基本流程是將水浮力減去結構自重計算出單位面積上錨桿需承擔的力，在假設錨桿受力均勻且滿足規(guī)范最小間距的前提下確定錨桿橫向及縱向布置間距，根據布置間距按式(2)計算出單根錨桿的軸向拉力，最后根據《巖土錨桿(索)技術規(guī)程(CECS22∶2005)》[2]驗算抗浮錨桿桿體截面積和錨固段長度。

常規(guī)設計方法計算簡便，能夠快速地進行錨桿的設計和布置，在實際設計中偏于安全。但是該方法假定各錨桿受力均勻，而在實際工程中底板變形往往較為復雜，導致錨桿實際受力是不均勻的，故常規(guī)設計方法可能造成結構和底板局部抗浮承載能力不足或錨桿布置浪費[3]。

1.2整體有限元計算法

實際情況下，錨桿的受力與上部結構荷載、底板和上部結構剛度、巖土層本身的力學性質等因素有關，故設計時可建立結構的整體有限元模型來計算。整體有限元計算法首先通過理論和試驗研究確定錨桿的線剛度和等效長度，在有限元模型中將錨桿體設為拉壓桿單元，即兩端點為鉸接點的桿單元，只承受軸向拉壓作用。該單元上部與底板結構相連，下部與地基相連。這種方法的特點是，當受到水浮力作用時可以較好地考慮工程中底板與地基之間的變形。但是，該方法需要建立結構的整體有限元計算模型，且計算中模型收斂性較差，設計過程復雜繁瑣，難以在工程中普遍推廣。

該方法中錨桿線剛度由下式求得[4]：

(3)

式中：li為錨桿存在軸力范圍內第i層土的厚度；

qi為單位長度內第i層土對錨桿的側摩阻力；

F0為錨桿頂端的軸拉力；

n為錨桿存在軸力范圍內土層數；

E為錨桿桿體的彈性模量；

A為錨桿橫截面積。

1.3底板變形修正法

前兩種方法都是目前工程中抗浮錨桿的常用設計方法，但在實際工程設計中兩種方法均存在一定局限性，本文在前兩種方法的基礎上提出了第三種方法——底板變形修正法，該方法在常規(guī)設計法的基礎上考慮了結構底板和土體之間的變形影響，同時相比整體有限元計算法更具有可操作性。

有限元計算結果顯示，底板變形較大部位的錨桿所受拉力較大，因而底板變形能在一定程度上表征錨桿拉力的大小，故可采用該錨桿處底板變形和整體底板變形的平均值之比，來修正錨桿的實際拉力。在實際工程中，錨桿距離中心越遠，其所受的拉力越大，這是因為遠離柱墩處底板受上部荷載的影響較小，而致水浮力作用下的底板向上變形大于柱墩附近底板，從而使得該處錨桿的拉力較大。此外，錨桿拉力還與錨桿錨固長度、巖土層基床系數以及錨固體本身的剛度有關，所以可引入變形修正因子θ對式(2)中單根錨桿的軸向拉力設計值Nt進行修正，即：

(4)

(5)

式中：si為第i根錨桿布置處底板在水浮力作用下的變形值，且取底板向上變形為正，可通過底板的撓度計算取得；

ai為第i根錨桿的作用影響面積；

n為錨桿總數。

由公式(4)、(5)可知，底板變形較大部位的錨桿受力較大，這和工程實際結果相符，由此布置錨桿可使得錨桿受力更為準確，并可充分利用錨桿的抗拉強度。底板變形修正法在常規(guī)設計法的基礎上考慮了底板變形對錨桿拉力的修正，在保證錨桿受力準確的同時又較整體有限元計算法有更好的可操作性。

2計算分析

以一典型單層地下室為例，其標準柱跨平面尺寸X、Y向均為8.4m×8.4m，混凝土強度等級為C30。地下室頂板覆土為1.2m，基礎形式為獨立基礎加防水板，地下室層高為4.2m，地下室底板厚300mm，計算取設計水浮力為50kN/m2。由于水浮力較大，底板下需設置抗浮錨桿。按常規(guī)設計方法初步計算并面狀均勻布置錨桿，錨桿平面布置見圖1，錨桿的間距為2.8m，單根錨桿的抗拔承載力特征值為190kN，按此計算抗浮錨桿進入黏土持力層不小于9.0m，錨桿孔直徑為200mm。錨桿錨筋采用3根20mm熱軋帶肋鋼筋(HRB400)，并用M30微膨脹水泥砂漿注漿。

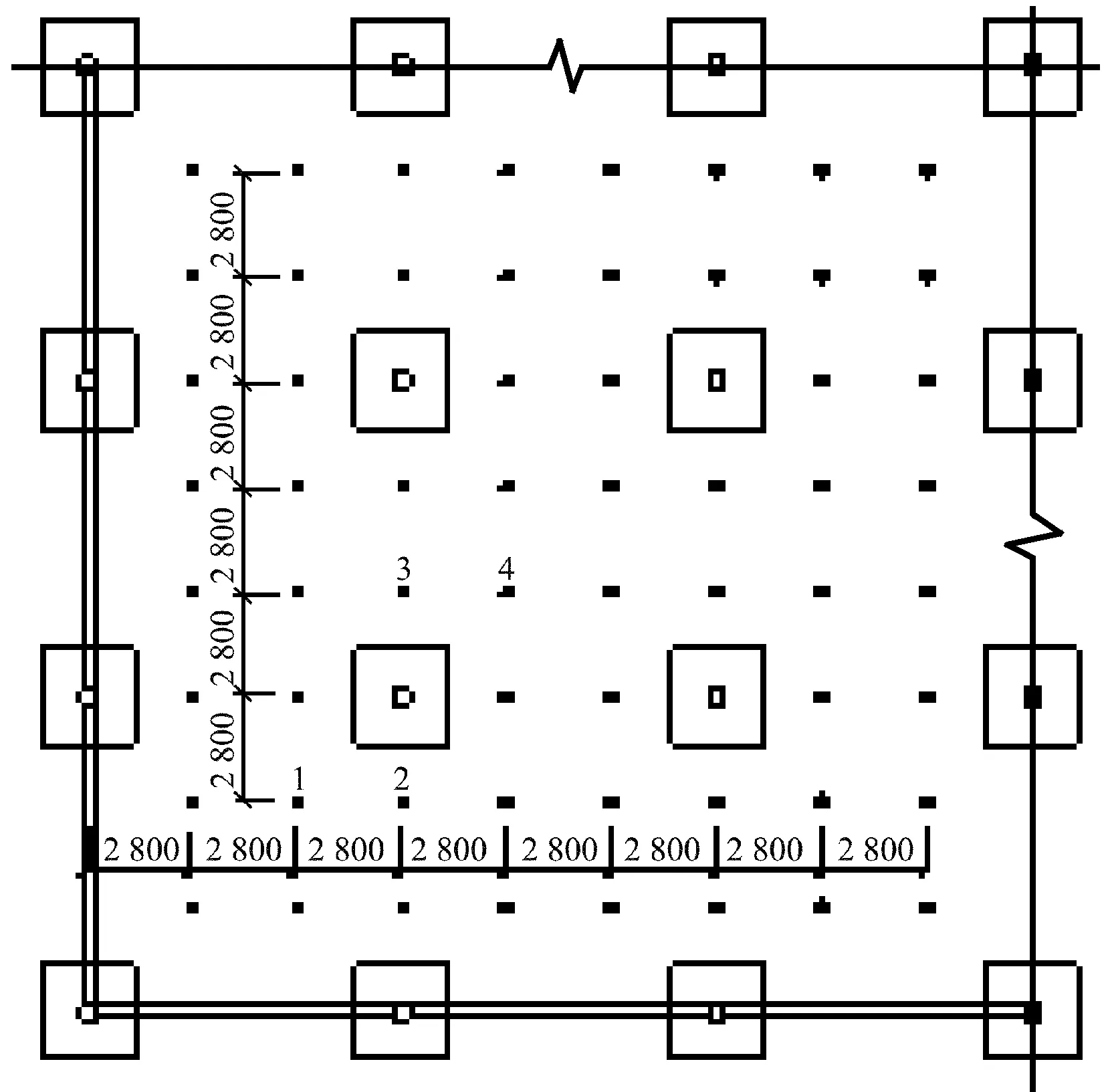
圖1　抗浮錨桿布置圖

整體有限元計算采用MidasGen進行，錨桿采用彈簧模擬，根據相關工程經驗及文獻[4]將彈簧的剛度系數取為100kN/mm，整體有限元計算模型見圖2，計算的變形結果見圖3。

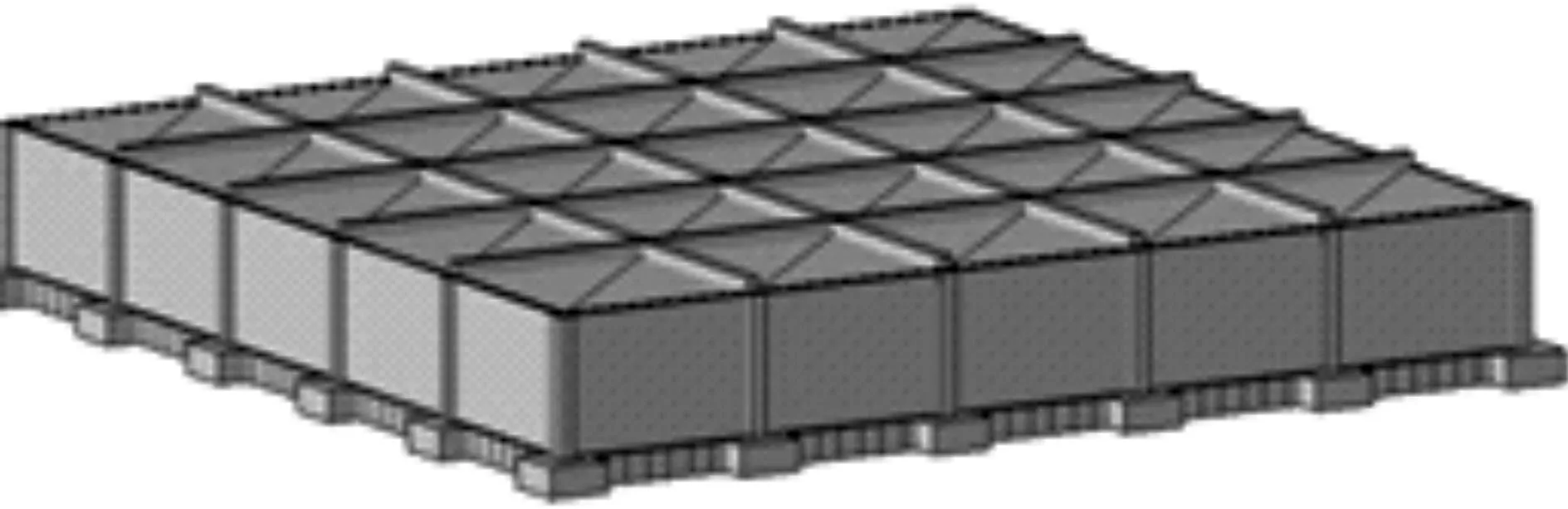
圖2　整體有限元計算模型

圖3　整體有限元計算底板變形圖

當采用底板變形修正法計算時，用SLABCAD軟件計算地下室底板的變形等值線圖，見圖4。

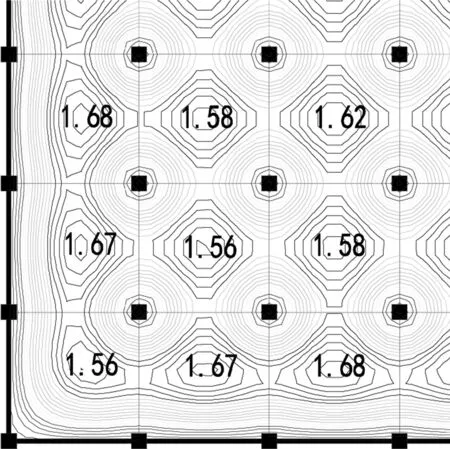
圖4　地下室底板變形圖

將3種方法計算得到的典型錨桿的軸向拉力進行對照，計算結果見圖5。由圖5可看出，整體有限元法和底板變形修正法的計算結果接近，而常規(guī)設計法的計算結果較為平均。這是由于常規(guī)設計法將地下室假定為一剛體，忽略了錨桿和底板、基礎剛度的差異產生的變形不均勻變化，從而導致部分柱跨中部錨桿承載力不足，基礎附近的錨桿承載力被高估。整體有限元計算法和變形修正法的計算結果均有相同規(guī)律，即錨桿距離柱越遠，其承擔的拉力越大，這是因為該處受上部荷載影響較小而致上浮作用下底板向上變形較大，從而使得錨桿拉力較大。

由圖5可見，底板變形修正法計算的錨桿拉力的最大值大于常規(guī)設計法計算結果的24%左右，最小值小于常規(guī)設計法計算結果的21%，故底板變形修正法的計算達到了重新分配錨桿內力的目的。

圖5　3種計算方法下的典型錨桿拉力

根據底板變形修正法計算的錨桿反力值見圖6。其中錨桿的最大拉力值為235kN，最小拉力值為149kN，基礎附近錨桿承載力存在不同程度富余。故可適當減小基礎附近錨桿的錨固長度，如圖6中可將基礎附近錨桿錨固長度縮短為7m，同時跨中錨桿受力較大區(qū)域的錨桿錨固長度增加至12m或增大錨桿體的直徑，這樣既加強了結構的安全性，又合理優(yōu)化了錨桿的布置，同時節(jié)約了工程造價。

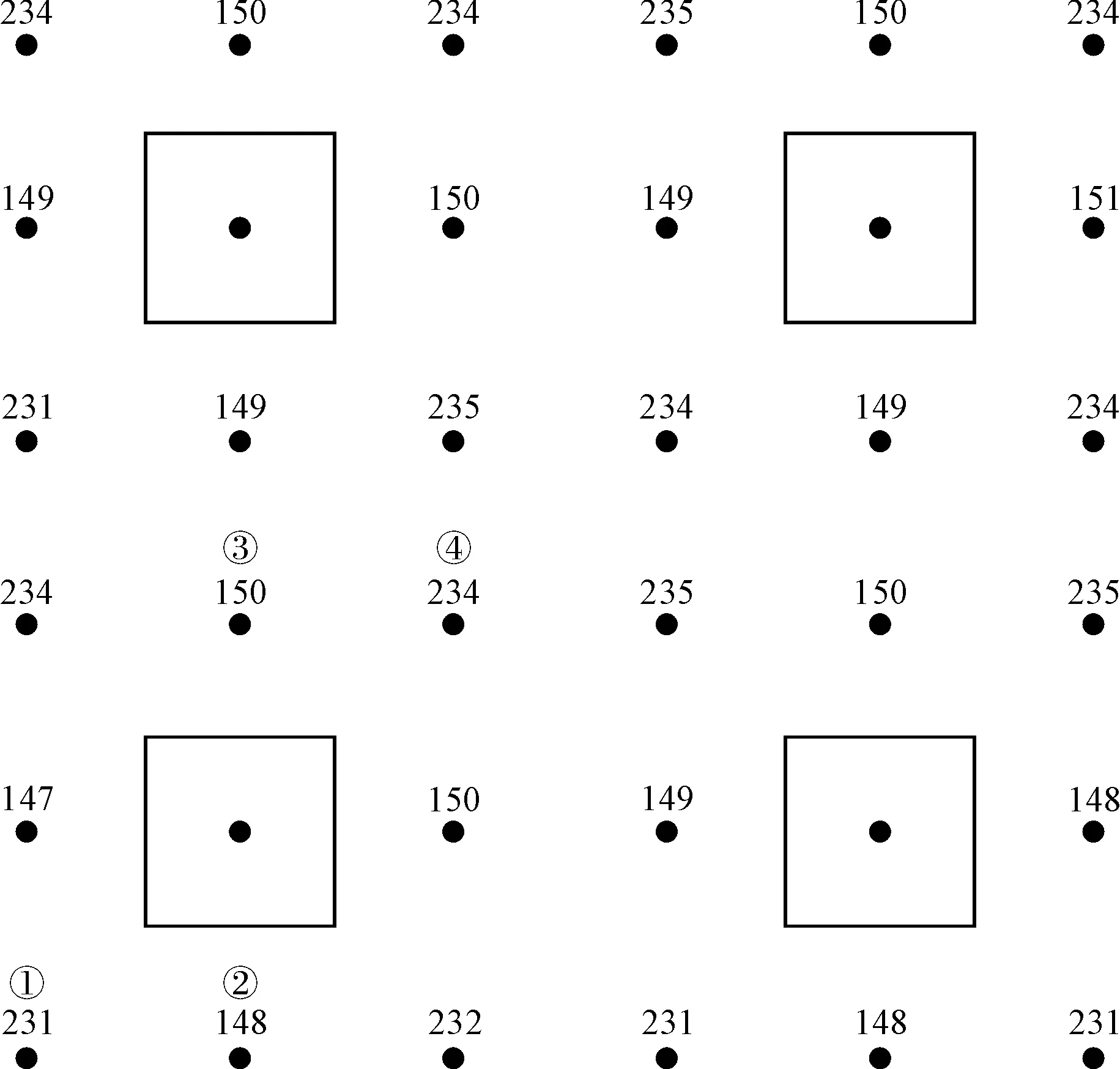
圖6　底板變形修正法計算的錨桿力/kN

3影響底板變形的主要因素

上述算例中，采用底板變形修正法計算不同底板剛度下錨桿拉力的變化情況見表1，表1中α1為最大錨桿力和常規(guī)設計法錨桿力的比值，α2為最小錨桿力和常規(guī)設計法錨桿力的比值。比較表1數值可見，隨著底板厚度的增加，底板剛度增大，底板的變形變小，其變形協(xié)調能力增強，錨桿最大拉力趨于減小，即當底板的板厚較小時，布置抗拔錨桿應特別注意；當底板的板厚足夠大時，即在水浮力的作用下接近一個剛體時，各區(qū)域的錨桿的拉力的差值接近于零，常規(guī)的計算方法就是基于此假定的，但這對于大部分工程并不適宜。

表1　不同底板剛度下錨桿力的變化

通過有限元模型模擬了不同錨桿線剛度下錨桿拉力的變化情況(表2)。

表2　不同錨桿剛度下錨桿力的變化

比較表2數值可見，隨著錨桿線剛度的增加，相當于底板基床系數相對于錨桿剛度減小，增強了錨桿自身的變形協(xié)調能力，故錨桿拉力的分布也將趨于均衡，但是隨著K值的增大，即錨桿體的性質由土層錨桿變?yōu)閹r石錨桿，錨桿拉力的變化差值并不明顯，直接采用底板變形修正法仍然可行。

4結語

本文介紹了錨桿抗浮計算的3種計算方法，通過分析結果可以得到以下結論：

1)錨桿受力并不是均勻的，其不均勻性既與底板剛度有關，也與錨桿線剛度和土層基床系數有關，在底板厚度較小的地下室采用土層錨桿抗浮時，常規(guī)設計方法有一定缺陷和安全隱患。

2)整體有限元法和底板變形修正法均能表征抗浮設計中錨桿的實際受力情況，而常規(guī)設計法的計算結果可能導致局部錨桿承載力不足。同時，底板變形修正法比整體有限元法更便于實際工程的計算。

3)采用底板變形修正法計算后，設計人員可更合理地設計、布置錨桿，保證結構的安全性，提高結構的經濟性。

參 考 文 獻

[1]中國建筑科學研究院.GB50009—2012建筑結構荷載規(guī)范[S].北京：中國建筑工業(yè)出版社，2012.

[2]中冶集團建筑研究總院.CECS22∶2005巖土錨桿(索)技術規(guī)程[S].北京：中國計劃出版社，2005.

[3]孫紹東，胡海濤，井彥青，等.抗浮錨桿合理設計探討[J].建筑結構，2013,43(22):80-85.

[4]孫仁范，劉躍偉，徐青，等.帶地下室或裙房高層建筑抗浮錨桿整體計算方法[J].建筑結構，2014,44(6):27-30.

收稿日期：2015-02-01

作者簡介：葉蓁(1982—)，男，浙江衢州人，工程師，從事建筑結構設計工作。

中圖分類號：TU473.1

文獻標志碼：B

文章編號：1008-3707(2016)05-0038-04

Anti-Floating Design Method of Anchor Taking intoAccount the Floor Deformation Correction

YE Zhen, TANG Hao