一種汽輪發電機組軸系受迫振動響應分析方法
劉博
(哈爾濱汽輪機廠,黑龍江 哈爾濱150040)
?
一種汽輪發電機組軸系受迫振動響應分析方法
劉博
(哈爾濱汽輪機廠,黑龍江 哈爾濱150040)
摘要:研究了汽輪發電機組的自由振動以及受迫振動響應問題,并通過特征值與特征向量的求解獲得了軸系的固有頻率和模態。并針對某型實際汽輪發電機組軸系,獲得了該軸系突加載荷時機組的扭轉振動響應。
關鍵詞:汽輪發電機組;受迫振動;瞬態響應
1 概述
受迫振動是指力學系統在外界周期驅動力作用下產生的一種振動。受迫響應振動分析通常包括兩個主要方面:正弦激勵下的穩態響應和隨時間變化的激勵扭矩下的瞬態響應。
對于穩態響應以及瞬態受迫響應,運動的矩陣方程可以采用模態轉換的方式進行解耦處理。對于穩態響應,列出的二階微分方程屬于封閉式。而對于瞬態激勵下的響應,可以通過數值積分的方法來進行計算。
受迫振動的一般運動方程為:
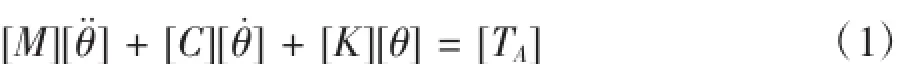
其中,[M],[C]和[K]為n×n階的方陣(n為模態中的節點數),分別對應著慣性矩陣、阻尼矩陣、剛度矩陣。方程中其它帶有θ的各向量,則分別對應了扭轉運動的加速度、速度、位移。[TA]為外力扭矩向量。
求解式(1)時,經常將變量從實際的物理響應值θ1…θn,轉化為模態坐標q1…qm的函數。在這里n代表節點數目,m代表所使用的模態數量。
模態轉化方程如下:
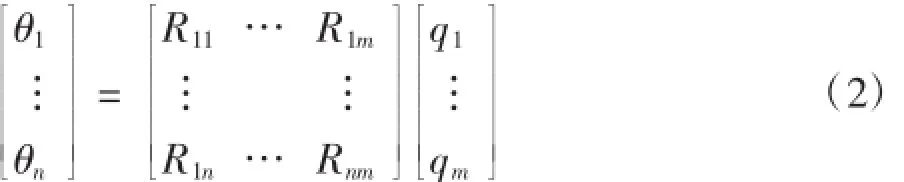
式(2)中的矩陣[R]包含了通過預先固有頻率計算得到的m個模態陣型。通過矩陣變換,將位移向量θ1…θn轉換為一個新的向量q1…qm.這個新的向量左乘模態陣型矩陣[R]所得到的矩陣,在任何時刻都等價于位移向量q1…qm.這個新的向量可以看成是模態系數。舉例來說,在任何時刻都可以表達出矩陣[R]中所列出的模態振型參與實際振動響應的情況。
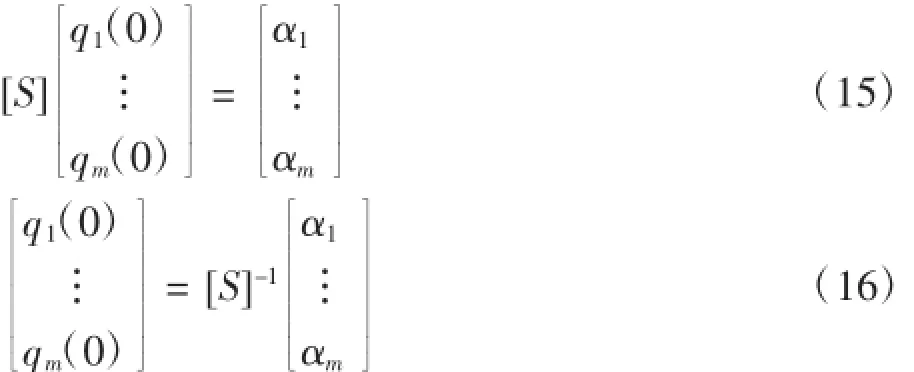
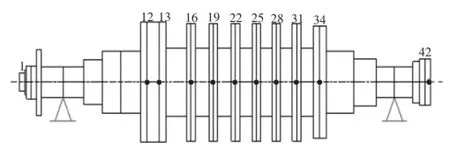
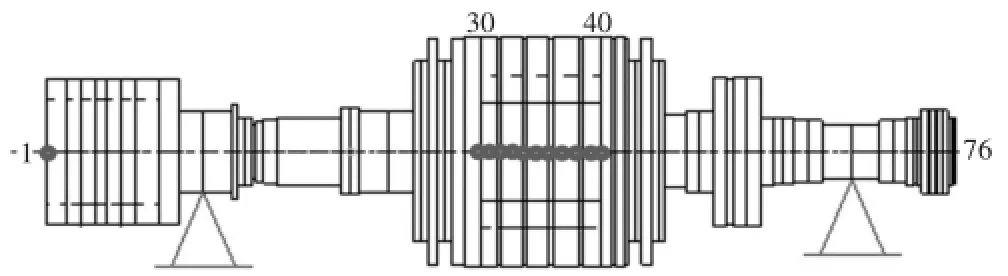
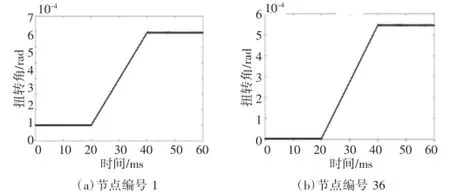
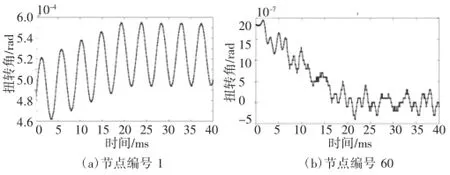
如果分析中用到了所有的n個模態振型,那么m=n,最終得到的分析結果將與不使用模態轉化方程的計算結果一致,相當于直接求解式(1)。如果只是選定的模態振型被使用,也就相當于m 將式(2)代入式(1),并進行矩陣變換 在這里[M'],[C']和[K']分別為模態轉動慣量矩陣、模態阻尼矩陣、模態剛度矩陣,它們都是m×m階矩陣,其中,m為所選擇的模態數量。另外,模態轉動慣量矩陣、模態剛度矩陣均為對角陣,這是因為固有振型為正交陣。試驗或者估測的模態阻尼值經常被直接添加進預設的阻尼矩陣中,這些預設的矩陣均為對角陣,并且非對角項均設為0.利用上述假設,運動模態方程變為非耦合,可以單獨的進行求解。[T'A]為外力扭矩模態向量,也同樣是m階。 穩態正弦激勵響應是在給定的外力扭矩向量下,得到各節點的穩態響應值,包括扭轉角位移、相位、振幅等。由于是在穩態的條件下,所以響應和激勵的頻率是一樣的。 在進行分析過程之前,首先要建立轉子振動的數學模型[1],包括阻尼特性、作用在每個節點上的外力扭矩幅值及相位、以及外力頻率ω.在本例中,外力扭矩向量元素TAI的形式為:Te(jωt+σ),其中j=.一般來說,作用在各節點上的外力扭矩的振幅和相位均不相同。除了給出外力扭矩幅值及相位外,激振頻率ω也必須給定。 如前所述,式(3)矩陣方程是非耦合的,也就是說,每個方程都可以單獨求解。列出r階模態方程如下, 矩陣變換得到, 在式(5)中,ωnr和ζr分別為無阻尼狀態下的固有頻率和r階模態下的無量綱阻尼率。 采用qrejωt形式的穩態正弦響應得到如下結果 因此 任一個向量都用同樣的方式求解 通過對式(8)中向量{q}量級的觀察,可以直觀的了解響應情況,因為通過向量{q}可以直觀的了解到在諧振頻率ω時,哪一階模態的響應最劇烈。 接下來可以將式(8)回代入到式(2)中,求得模態中n個節點處的旋轉角位移的幅值和相位,最終得到受迫振動的響應分析結果。 本節所要討論的問題是響應的時域分析,既所得到的結果為時間的函數,在給定的隨時間變化的外力扭矩向量下,得到各節點的扭轉角位移、響應扭矩[2]。 分析過程中的已知項為轉子振動的數學模型,包括阻尼特性,以及隨時間變化的外力扭矩。 待解模態方程如下, T'r(t)為隨時間t變化的r階模態下的外力扭矩,M'rr為r階模態下的轉動慣量。 方程(9)通常在將二次方程降階為兩個一次方程后,采用數值積分的方法進行求解。 令 因此 將式(5)代入(4)得 對于數值積分求解,必須要提供qr和它的一階導數的初始條件(Y1r(0)和Y2r(0)),上述初始條件可以通過以下的矩陣變換,由確定的角位移及速度矢量的初始條件求得,由式(2)可得 上述方程左側的矩陣,包含了n階指定的角位移初始條件(t=0時刻),而在方程右側,包含了m階待求位移初始條件。因此 為了方便起見,定義[S]=[R]T[R],[S]為m×m矩陣,同樣定義包含m元素的{α} 因此, 加速度的初始條件計算方法與速度的計算方法類似 到此為止,對于1階方程(5)和(6),每一節點上的初始條件都已經具備了,包括q以及它的一階導數,這樣我們就可以應用數值積分進行求解。 在進行數值積分的過程中,一般要設定一個足夠小的積分時間段,以保證結果的穩定。時長大約應為分析中最高頻率周期的四分之一左右[3]。 4.1模型簡化 根據有限元理論,對汽輪機轉子進行有限元模型軸段劃分[4],劃分結果如圖1所示。 圖1 汽輪機轉子有限元模型 圖中節點編號未全部標出,如圖中所示,從汽輪機的左端起依次進行編號。圖中黑色圓點表示汽輪機轉子扭矩加載的位置,12、13、16、19、22、25、28、31、34汽輪機均布載荷點,節點42為負載載荷加載點。 對電機轉子進行有限元模型軸段劃分,劃分結果如圖2所示。 圖2 電機轉子有限元模型 圖中節點編號未一一標出,如圖中所示,從電機轉子的左端起依次進行編號。圖中灰黑的點表示電機轉子扭矩的加載位置,其中,節點1為輸入扭矩加載點,節點30至40為電機負載扭矩的均布加載點。 4.2突加載荷時機組的振動特性結果與分析 4.2.1突加載荷時汽輪機振動特性 汽輪機轉子空載運轉穩定的情況下,在20 ms內突加額定載荷,對汽輪機轉子的振動特性進行分析。載荷的加載方式,根據功率5 MW計算得到總扭矩-7 150.88 N·m,并將其加載在汽輪機的末端截面,將均布載荷794.54 N·m加載在汽輪機各輪盤節點。在0~20 ms之間,汽輪機處于空載穩定運行階段;在20~40 ms之間,汽輪機末端載荷由0變化到-7 150.88 N·m;在40~60 ms之間,汽輪機處于滿載穩定運行階段。以汽輪機末端節點42為基準,選取關鍵節點考察扭轉角隨時間的變化,得到結果如圖3所示。 圖3 各節點扭轉角隨時間變化比較 由突加載荷時,汽輪機各選取節點扭轉角隨時間的變化可以看出,汽輪機各節點的扭轉角隨載荷的增加而不斷增加,并有很小的波動,加載結束后轉子各截面扭轉角在固定值附近小幅波動,波動是由于轉子的轉動引起。 4.2.2突加載荷時電機轉子振動特性 電機轉子空載運轉穩定的情況下,在20 ms內突加額定載荷,對電機轉子的振動特性進行分析。載荷的加載方式為:在電機的首端面加載由功率5 MW計算得到的總扭矩31 830.98 N·m并保持不變,電機上的負載載荷均布加載電機30~40的各節點上。在0~20 ms之間,電機各均布載荷由0變化到額定載荷;20~40 ms之間,電機為滿載載荷穩定運轉階段。以電機末端節點76為基準,選取幾個關鍵節點考察扭轉角隨時間的變化,得到結果如圖4所示。 圖4 各節點扭轉角隨時間變化比較 突加載荷時,由選取各節點扭轉角隨時間變化圖可以看出,在電機負載扭矩和電機首端加載扭矩之間的節點,其扭轉角隨時間變化為波形,在突加載荷時,扭轉角隨電機負載的增加而增加;在電機負載扭矩節點至電機末端之間的各節點,扭轉角隨時間變化為多個頻率的波形疊加形式,并且其值隨電機負載的增加而減小。 本文提出了一種計算汽輪發電機組軸系受迫振動響應的分析方法,并利用相關程序對于實例進行 了計算工作,驗證了該方法能夠合理準確的對于機組的受迫振動瞬態響應進行分析、模擬。 參考文獻: [1]楊建國,夏松波,劉永光,等.旋轉機械整機固有特性分析[J].汽輪機技術,1998,40(6):329-331. [2]陸明萬,羅學富.彈性理論基礎[M].北京:清華大學出版社,2001:78-99. [3]傅行軍.汽輪發電機組扭振[M].北京:中國電力出版社,1997:3-7. [4]王勖成.有限單元法[M].北京:清華大學出版社,2003:55-63. 中圖分類號:TK261 文獻標識碼:A 文章編號:1672-545X(2016)04-0037-03 收稿日期:2016-01-19 作者簡介:劉博(1982-),男,黑龍江哈爾濱人,本科,工程師,從事汽輪機組設計分析工作。 A Turbo-Generator Set Shafting Forced Vibration Response Analysis Method LIU Bo Abstract:This paper studies steam turbine generator set free vibration and forced vibration response of the problem,obtained shafting natural frequency and modal by solving eigenvalue and eigenvector.For a certain type of actual steam turbine generator shaft,calculate the shafting torsional vibration response of the unit when a sudden load happen. Key words:steam turbine generator unit;forced vibration;transient response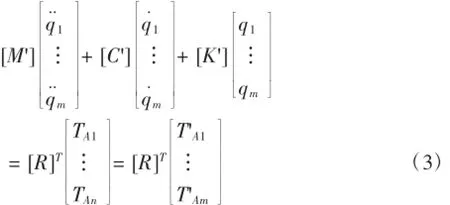
2 穩態正弦激勵響應
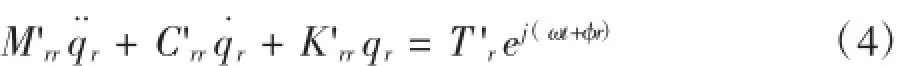

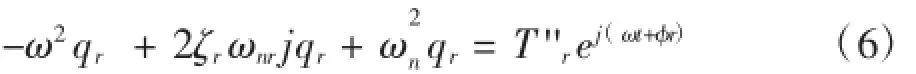
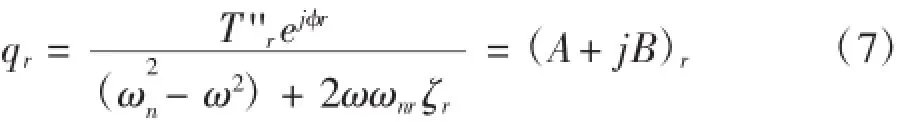
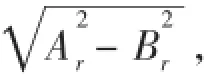

3 瞬態響應分析
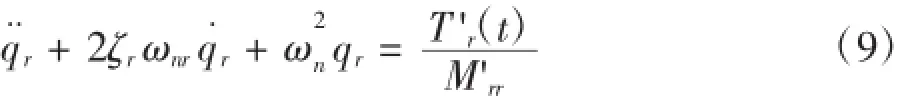


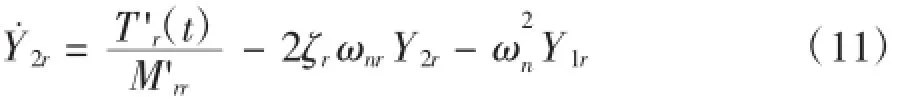

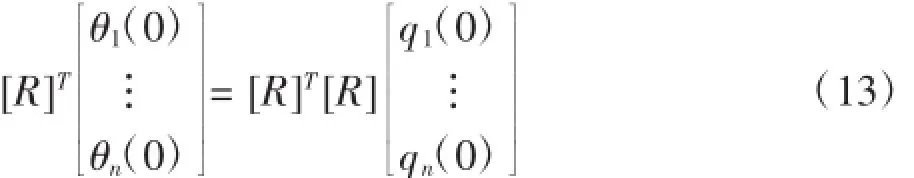


4 實例計算
5 結束語
(Harbin Steam Turbine Plant,Harbin Heilongjiang 150040,China)

