一種六自由度工業機器人運動學分析及三維可視化仿真

高　藝　馬國慶　于正林　曹國華

長春理工大學，長春，130022

?

一種六自由度工業機器人運動學分析及三維可視化仿真

高藝馬國慶于正林曹國華

長春理工大學，長春，130022

摘要：針對Motoman-HP20機器人的構型特點，采用D-H坐標變換法建立其運動學坐標系，將機器人分解為位置結構和姿態結構，得到以位置矢量和歐拉角表示的完備廣義坐標，利用位姿分離法對機器人進行逆運動學求解，求得各個關鍵轉角。構建了三維可視化仿真環境，驗證所提出的運動學算法的正確性。該仿真環境可以直觀地觀察機器人各部分的運動情況。

關鍵詞：工業機器人；運動學分析；可視化仿真；軌跡規劃

0引言

從第一臺機器人Unimate誕生至今，經過半個世紀的發展，工業機器人技術已相當成熟，重復定位精度高、運動速度快、程序柔性好等優點使其得到廣泛應用[1]。但是市場上的商用工業機器人控制系統大都是對外封閉的，很少提供二次開發的接口，這給具有特殊作業要求的機器人系統開發和系統集成帶來了困難。對工業機器人運動學的研究可以有效地了解機器人的奇異點的存在情況以及運動過程中的干涉情況，為軌跡規劃提供技術基礎，因此研究工業機器人的運動學問題非常必要[2-3]。

機器人的運動分析是實現機器人運動控制和軌跡規劃的基礎，它包括正運動學和逆運動學兩部分。目前，機器人正運動學的求解方法主要有D-H坐標變換法和四元數法[4]；機器人逆運動學的求解方法主要有解析式法、幾何法以及智能算法[5]。隨著可視化技術的發展，越來越多的人將可視化仿真的方法應用于機器人的運動學求解，從而直觀地監控機器人各關節的運動情況。Corke[6]開發了Robotics Toolbox機器人工具箱，該工具箱可實現機器人的運動仿真和軌跡規劃，但其連桿不能表達真實機器人的三維尺寸，在碰撞檢測方面的效果并不理想。李憲華等[7]以川崎FS03N機器人為研究對象，利用三維軟件完成該機器人的實體建模，編寫 SolidWorks軟件和MATLAB的接口函數，構建基于MATLAB的3D仿真平臺，通過運動仿真的方式驗證了運動學的正確性。

本文以Motoman-HP20機器人為研究對象，采用D-H坐標變換法建立機器人的連桿坐標系，得到以位置矢量和歐拉角表示的正運動學方程，通過臂腕位姿分離法對機器人進行逆運動學求解，根據最短行程原則從多組逆解中選擇出最適合的一組解。最后基于Dmworks軟件構建三維可視化仿真環境，驗證運動學求解的正確性。

1運動學求解

與動力學求解過程相比，運動學的求解過程并不考慮各桿件之間的相互作用力，只是研究其運動關系。正運動學問題是：在已知各關節角及桿件尺寸的基礎上，求解工具坐標系在基坐標系下的位姿。逆運動學問題是：在已知工具坐標系相對于基坐標系的期望位姿和桿件的幾何尺寸的情況下，求取機器人工具坐標系達到此位姿時各個關節的角度值。

1.1連桿坐標系的建立

Motoman-HP20是一款具有6個旋轉關節的串聯機器人，根據Motoman機器人的基坐標系設置原則和標準D-H坐標系建立準則，該機器人基坐標系x0y0z0的原點位于關節1的軸線上，同時也位于關節1軸線和關節2軸線的公垂線上，即二者的交匯處。依次建立各個關節處的坐標系，x6y6z6為機器人工具坐標系，其中后三個關節的坐標系交匯于一點。機器人D-H坐標系如圖1所示。

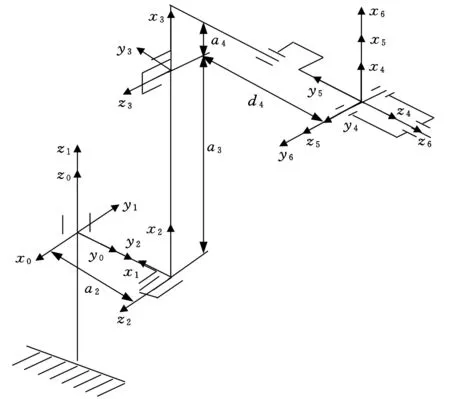
圖1　Motoman-HP20機器人D-H坐標系

1.2正運動學求解

根據D-H坐標系建立準則可以確定圖1中相鄰兩個坐標系之間的轉換關系，同時根據該機器人的幾何尺寸可確定機器人的D-H參數，如表1所示。對于關節型機器人而言，只有關節角βi為變量，兩關節軸扭角αi、連桿長度ai、兩連桿間偏置距離di均為常量。

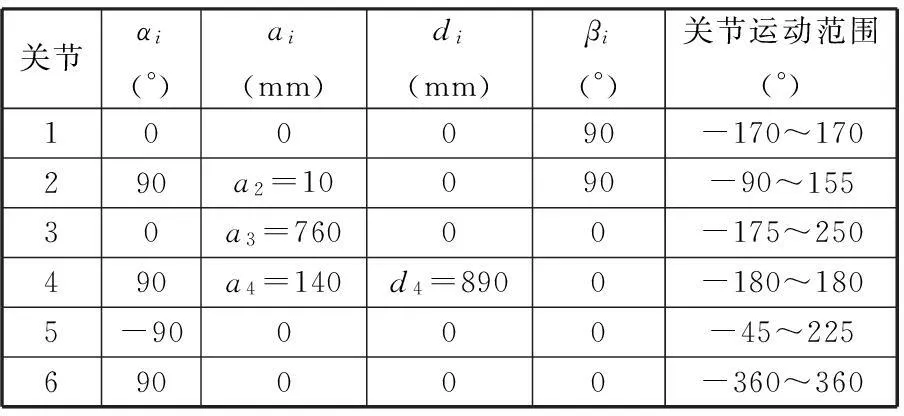
表1　HP20機器人D-H參數

機器人相鄰關節坐標系間的轉換矩陣[8]為

i-1Ti=Rot(z,βi)·Trans(0,0,di)·

Trans(ai,0,0)·Rot(x,αi)=

(1)

式(1)表示的是相鄰兩個坐標系之間的變換關系，將其順次相乘可以得到工具坐標系在基坐標系下的變換矩陣：

(2)

nx=c1[c23(c4c5c6-s4s6)-s23s4c6]+

s1(s4c5c6+c4s6)

ny=s1[c23(c4c5c6-s4s6)-

s23s4c6]-c1(s4c5c6+c4s6)

nz=-s23(c4c5s6-s4s6)+c23s4c6

s1(s4c5c6-c4c6)

c1(s4c5c6-c4c6)

oz=-s23(c4c5s6+s4c6)-c23s5s6

ax=c1(c23c4s5+s23c5)+s1s4s5

ay=s1(c23c4s5+s23c5)-c1s4s5

az=s23c4s5-c23c5

px=c1(a4c23+d4s23+a3c2+a2)

py=s1(a4c23+d4s23+a3c2+a2)

pz=a4s23-d4c23+a3s2

ci=cosβi,si=sinβi

cij=cos(βi+βj)

sij=sin(βi+βj)

i=1,2,…,6;j=1,2,…,6

式(2)即為運動學正解，將表1中D-H參數代入式(2)可求得相應元素值。

由式(2)可以看出，該齊次變換矩陣包含了機器人工具坐標系到基坐標系的位姿信息，其中[noa]為姿態矩陣，p=(px,py,pz)為工具坐標系的位置矢量。用齊次變換矩陣表示剛體的轉動雖然簡化了運算，但需要9個元素來完全描述剛體的位姿，且它給出的是一組非完備的廣義坐標。而在實際應用中工業機器人的位姿一般采用一組完備的廣義坐標(px,py,pz,φ,θ,ψ)來表示。歐拉角的轉動矩陣表達式為

(3)

s=sin,c=cos

令式(2)中的姿態矩陣與歐拉角的轉動矩陣(式(3))的元素對應相等，得到一組完備的廣義坐標(φ,θ,ψ)，求得

φ=arctan(ay/ax)

θ=arctan((axcφ+aysφ)/az)

ψ=arctan((nycφ-nxsφ)/(oycφ-oxsφ))

圖1所示的位姿為HP20機器人的機械零位，但通過D-H法建立的坐標系關節角卻為(90°，90°，0°，0°，0°，0°)，因此在構建三維可視化仿真環境的時候需要進行轉換處理。

1.3逆運動學求解

根據HP20機器人構型特點，其后3個關節坐標系交匯于一點，故該機器人的位置僅由前3個關節變量決定，姿態僅由后3個關節變量決定。因此可采用位姿分離法來求解該機器人運動學的逆解。

(1)求解β1。將0T6=0T11T22T33T44T55T6左右兩邊各左乘(0T1)-1，則有

(0T1)-10T6=

(4)

令

(5)

取其中第4列

由于式(4)和式(5)矩陣第2行第4列對應相等，所以有

-s1px+c1py=0

(6)

則β1=arctan(py/px)。

(2)求解β3。由于式(4)和式(5)矩陣的第1行第4列及第3行第4列分別對應相等，所以有

c1px+s1py=a4c23+d4s23+a3c2+a2

(7)

pz=a4s23-d4c23+a3s2

(8)

對式(6)～式(8)分別取平方然后相加可得

μ=ρcosηc3+ρsinηs3

(3)求解β2。將0T6=0T11T22T33T44T55T6左右兩邊各左乘(0T11T22T3)-1，得

3T44T55T6=

(9)

令

(10)

其第3列和第4列元素分別為

由于式(9)和式(10)矩陣的第1行第4列及第2行第4列分別對應相等，所以有

a4=c1c23px+s1c23py+s23pz-a3c3-a2c23

-d4=-c1s23px+s1s23py+c23pz+a3s3+a2s23

β23=

可得β2=β23-β3。

(4)求解β4。由于式(9)和式(10)矩陣的第1行第3列及第3行第3列分別對應相等，所以有

c4s5=c1c23ax+s1c23ay+s23az

s4s5=s1ax-c1ay

當s5≠0時

當s5=0時，關節4和關節6重合，機器人退化為5自由度，此時，β4可以為任意值，一般定義為當前值。

(5)求解β5。將0T6=0T11T22T33T44T55T6左右兩邊左乘(0T11T22T33T4)-1，得

(11)

令

(12)

由于式(11)和式(12)矩陣的第1行第3列及第3行第3列分別對應相等，所以有

s5=ax(c1c23c4+s1s4)+ay(s1c23c4-c1s4)+azs23c4

c5=c1s23ax+s1s23ay-azc23

β5=arctan(s5/c5)

(6)求解β6。由于式(11)和式(12)矩陣的第2行第1列及第2行第2列分別對應相等，所以有

s6=nx(s1c4-c1c23s4)-ny(s1c23s4+c1c4)-nzs23s4

c6=ox(s1c4-c1c23s4)-oy(s1c23s4+c1c4)-ozs23s4

β6=arctan(s6/c6)

1.4解的對應關系

通過位姿分離變量法可得到該機器人的各關節角度值，共有可能的8組解。但是在實際的控制系統中，由于關節角度范圍等因素的限制，實際只能取其中的一組作為最終的可行解。可行解的篩選原則主要有行程最短原則、能量消耗最小原則、運動最平穩原則等，結合HP20機器人構型特點，本文選取行程最短原則作為逆解篩選原則。最短行程原則算法流程如圖2所示，其中βcm表示機器人當前第m關節的角度值，βnm表示機器人逆解第n組第m關節的角度值，n=1,2,…,8;m=1,2,…,6。

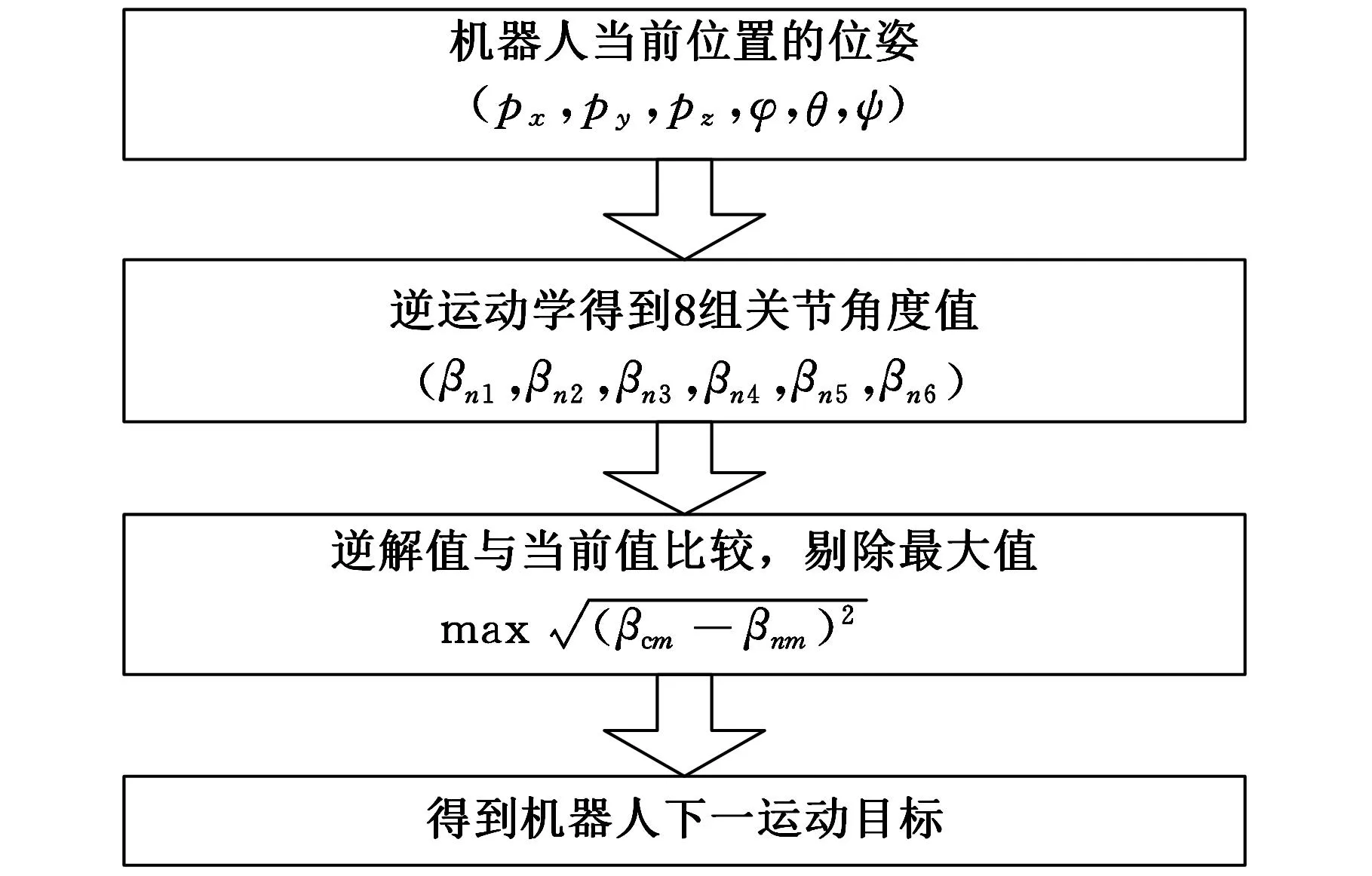
圖2　最短行程原則算法流程圖

2三維可視化仿真環境的建立

機器人三維可視化仿真是借助于計算機技術和三維建模技術構建起來的，它既能體現真實機器人的尺寸模型又具有真實機器人系統的運動學關系，可有效地驗證運動學算法以及運動的可視化。

2.1三維模型的建立

三維建模軟件具有強大的建模功能，可解決通用編程語言構建模型能力不強的問題，根據HP20機器人的特點，嚴格按照真實機器人的尺寸進行建模，將機器人模型分為7個部分，各部分如圖3所示。

圖3　機器人各部分模型

2.2三維可視化仿真環境的構建

將圖3各部分模型分別導入DMworks軟件，然后創建包含運動學關系的機器人設備，根據連接關系依次插入從而完成整個機器人設備的創建，然后設置關節類型和關節驅動、設置轉角范圍和工具中心點(tool center point, TCP)坐標，使其具有運動學的關系，三維仿真圖形界面如圖4所示。

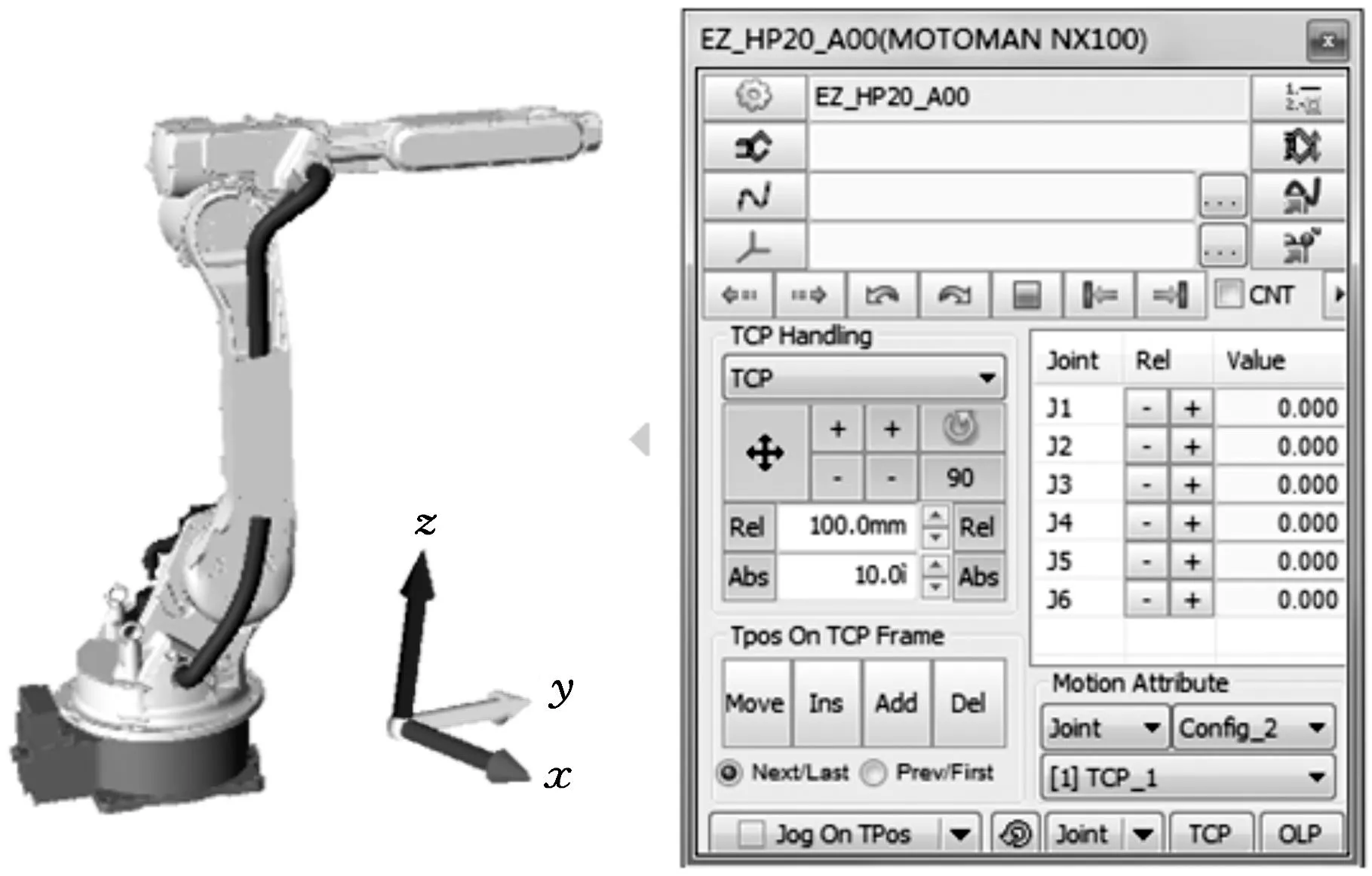
圖4　三維可視化仿真界面

3基于三維可視化仿真的運動學算法驗證

3.1正運動學算法驗證

可視化仿真環境中機器人初始位姿為HP20機器人的機械零位，但通過D-H法建立的坐標系關節角卻不全為0°，為使兩者統一，在構建可視化平臺時進行轉換處理。圖4中坐標指示方向與圖1中基坐標系方向完全一致。在可視化仿真平臺中選取5組特殊臂型來驗證所提正運動學求解算法的正確性。5組臂型下機器人工具坐標系在基坐標系下位置矢量如表2所示，其臂型如圖5所示。

表2　正運動學驗證數據

圖5　機器人幾種臂型

由表2可看出： ①各關節角均為0°，處于機械零位，此時工具坐標系在基坐標系下位置矢量為(0，1050，900)mm;②其他關節為0°，第1關節為90°，此時工具坐標系在基坐標系下位置矢量為(-1050， 0，900)mm;③其他關節為0°，第2關節為90°，此時工具坐標系在基坐標系下位置矢量為(0，1050，-900)mm;④其他關節為0°，第3關節為90°，此時工具坐標系在基坐標系下位置矢量為(0，10，1660)mm;⑤其他關節為0°，第5關節為90°，此時工具坐標系在基坐標系下位置矢量為(0，945，1005)mm。

圖5所示的臂型與表2中的數據一一對應，從而驗證了所提出的運動學正解算法的正確性。

3.2逆運動學算法驗證

逆運動學采用如下驗證方法： ①隨機取關節角為(30°，20°，-40°，-60°，50°，10°)的一組值，通過正運動學得到機器人此刻的位姿為(-438.301，898.477，57.334，-142.192，-62.472，33.366)mm；②將此組位姿值作為逆運動學求解的輸入，得到機器人的可能存在的8組解；③將8組解逐組再用正運動學算法進行求解，得到每組關節角對應的位姿，對比每組關節角的姿態與原隨機關節角輸入時的位姿關系。

按照上述步驟得到8組關節角如表3所示，各組關節角對應的位姿如圖6所示。每組關節角的姿態與原隨機關節角輸入時的位姿均相同，從而驗證了逆運動學算法的正確性。

表3中給出了通過逆運動學求解得到的8組關節角，其中第3組關節5的角度、第5組關節2和關節5的角度以及第6組關節2的角度超出了表1中所給的對應關節運動范圍，這說明雖然在理論上HP20機器人的運動學存在8組解，這是由于解反三角函數產生多解造成的，但是在實際系統中會因為電機轉角限制、線纜纏繞、桿件干涉等因素導致表3中第3、5、6組關節角形成的位姿雖然在可視化仿真過程中可以顯示，但現實中不能實現，這也恰恰說明了1.4節運用行程最短原則確定逆運動學的一組最優解的重要性。

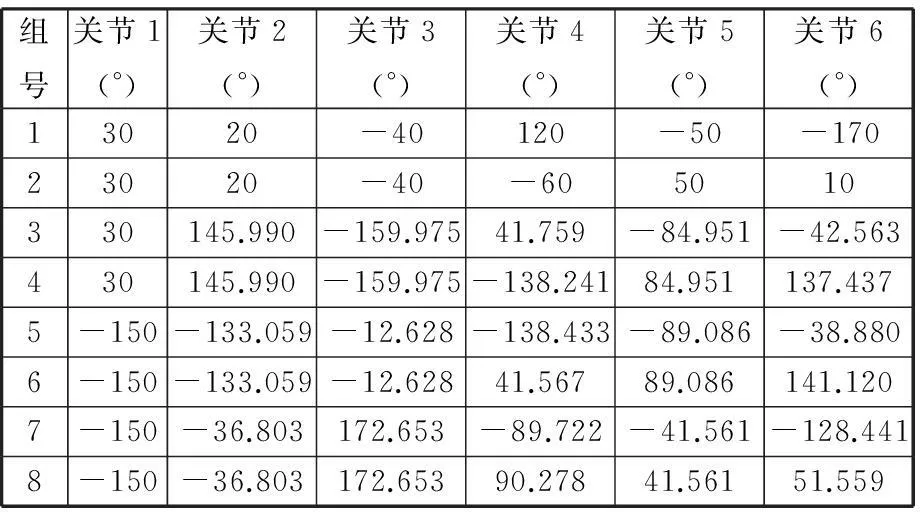
表3　HP20機器人逆運動學驗證表

圖6　運動學逆解8組位姿

4結束語

本文以Motoman-HP20機器人為研究對象，采用D-H坐標變換法建立機器人的連桿坐標系，得到了以位置矢量和歐拉角表示的正運動學方程，通過臂腕位姿分離法對機器人進行逆運動學求解，最后構建三維可視化仿真環境，驗證所提出的運動學算法的正確性。該仿真平臺可以直觀地觀察機器人各部分的運動情況，從而為后續可視化的軌跡規劃奠定基礎。

參考文獻：

[1]王田苗,陶永. 我國工業機器人技術現狀與產業化發展戰略[J]. 機械工程學報，2014,50(9)：1-13.

Wang Tianmiao,Tao Yong. Research Status and Industrialization Development Strategy of Chinese Industrial Robot[J]. Journal of Mechanical Engineering, 2014,50(9)：1-13.

[2]Albu-Schaffe A，Haddadin S，Ott C H．The DLR Lightweight Robot: Design and Control Concepts for Robots in Human Environments[J]．Industial Robot，2007，34(5)：376-385．

[3]倪受東,張敏,盛志剛. 基于開放式平臺的視覺工業機器人研究[J].制造業自動化，2014，36(2)：44-48.

Ni Shoudong, Zhang Min, Sheng Zhigang. The Research on Visual Industrial Robot Based on Open Platform[J]. Manufacturing Automation，2014，36(2)：44-48.

[4]何慶稀,游震洲,孔向東．一種基于位姿反饋的工業機器人定位補償方法[J]．中國機械工程，2016，27(7)：872-876．

He Qingxi, You Zhenzhou,Kong Xiangdong. Positioning Error Compensation Method of Industrial Robot Based on Closed-loop Feed Back of Position and Orientation[J]. China Mechanical Engineering, 2016，27(7)：872-876．

[5]李瑞峰,馬國慶. 基于MATLAB仿人機器人雙臂運動特性分析[J].華中科技大學學報(自然科學版),2013,41(增刊1)：343-347．

Li Ruifeng,Ma Guoqing. Dual-arm Kinematic Characteristics Analysis of Humanoid Robot Based on Matlab[M]. J. Huazhong Univ. of Sci. & Tech. (Natural science Edition),2013,41(S1)：343-347．

[6]Corke P．Robotics，Vision and Control[M]．Berlin: Springer-Verlag，2011．

[7]李憲華,郭永存,宋韜．六自由度工業機器人手臂正運動學分析與仿真[J]．安徽理工大學學報(自然科學版)，2013，33(2)：34-38.

Li Xianhua, Guo Yongcun, Song Tao. Forward Kinematics Analysis and Motion Simulation Platform of a Six DOF Industrial Manipulator[J]. Journal of Anhui University of Science and Technology( Natural Science),2013，33(2)：34-38.

[8]蔡自興.機器人學基礎[M].北京:機械工業出版社，2009.

(編輯蘇衛國)

收稿日期：2015-12-28

基金項目：國家高技術研究發展計劃(863計劃)資助項目(2013AA2400 )；吉林省科技發展計劃資助項目(20100365 )；吉林省省級產業創新專項資金資助項目(2016C088)

中圖分類號：TP242

DOI：10.3969/j.issn.1004-132X.2016.13.005

作者簡介：高藝，女，1968年生。長春理工大學機電工程學院副教授。主要研究方向為機電系統控制理論與控制技術。馬國慶，男，1988年生。長春理工大學機電工程學院助教、博士研究生。于正林，男，1971年生。長春理工大學機電工程學院教授。曹國華，男，1965年生。長春理工大學機電工程學院教授。

Kinematics Analysis of an 6-DOF Industrial Robot and Its 3D Visualization Simulation

Gao YiMa GuoqingYu ZhenglinCao Guohua

Changchun University of Science and Technology,Changchun,130022

Abstract:For configurational characteristics of Motoman-HP20 robot, the D-H coordinate transformation method was adopted to establish the kinematics coordinate system, the robot was decomposed into position structure and pose structure, complete generalized coordinates of position vector and Euler angle were obtained. Pose separation method was used to analyse the robot inverse kinematics solution for critical angle. The 3D visual simulation environment was built, and the kinematics of the proposed algorithm was proved to be correct. The simulation platform of robot movement of each part could be observed visually.

Key words:industrial robot; kinematics analysis; visualization simulation;trajectory planning