變載荷條件下的滾動軸承在線故障診斷方法

蔣麗英，李茜茜，崔建國，席劍輝

(沈陽航空航天大學 自動化學院, 沈陽 110136)

機械設備運轉過程中載荷、轉速的變化以及設備故障產生的沖擊、摩擦等因素均會導致滾動軸承振動信號具有非平穩性[1]。經驗模態分解(Empirical Mode Decomposition，EMD)[2-5]和小波分析[6-8]是近年來廣受矚目的非平穩信號處理技術。EMD雖然是一種自適應信號處理方法，但計算量大，且本征模式分量的總數、頻率及計算時間都具有不確定性，響應時間上難以滿足在線實時診斷的要求；小波分析存在的突出問題是目前尚無有效方法解決最優小波基的選擇，并且其計算量隨分解層次的增加而增加；在線處理非平穩信號時，以上2種方法在線計算量太大，難以滿足在線故障診斷對實時性的要求。

Fisher判別式分析(Fisher Discriminant Analysis，FDA)是一種降低特征空間維數的線性模式分類方法，被廣泛地應用于模式識別和故障診斷[9-10]等領域。由于滾動軸承結構對稱，載荷區間位置固定，其振動信號的非平穩性表現為周期平穩性；因此，結合動態主分量分析的思想，提出了一種帶時延窗口動態FDA(DFDA)的在線故障診斷方法。

DFDA通過引入時延窗口的方式捕獲滾動軸承振動信號的周期平穩性，即由當前時刻和前d個時刻振動信號所構成的增廣向量作為故障特征向量，并根據已知故障的歷史數據建立FDA故障診斷模型。為了使滾動軸承在線故障診斷具有魯棒性，即在一定載荷參數攝動下故障診斷系統仍具有較好的診斷性能，選取不同載荷條件下的試驗數據對DFDA的有效性進行了驗證。

1 Fisher判別式分析

FDA的基本思想是按照最大化類間離散度、同時最小化類內離散度的準則，尋找一個從高維向低維空間映射的線性變換矩陣，從而獲得最佳判別矢量空間(FDA空間)，使故障模式在該空間內有最佳的可分離特性。

1.1 FDA的基本原理

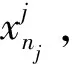
(1)

同理，將p種已知故障類的樣本數據矩陣按列的方向依次放入一個新的矩陣中，則獲得構成一個n行m列的總體樣本數據矩陣X，即

X=[(X1)T(X2)T… (Xp)T]T，

(2)

(3)

(4)

(5)

St=Sw+Sb，

其中，Sj為第j類的類內離散度矩陣，即

(6)

在非小樣本情況下，求解最優FDA向量問題可歸結為如下問題，即

Sbwj=λjSwwj；j=1,2,…,p-1，

(7)

式中：wj為第j個FDA向量。將p-1個FDA向量按特征值λj從大到小排列成新矩陣Wp，即

(8)

Wp∈m×(p-1)為判別權矩陣，亦稱為FDA模型。因此，通過判別權矩陣Wp，數據從原始m維空間投影到p-1維判別空間，實現了不同類別數據的最優分離。其線性變換關系可表示為

(9)

其中:zi∈(p-1)×1，稱為判別得分向量。

1.2 低維FDA空間的確定

盡管經過FDA變換后可得到較低維的判別空間，但當FDA應用到獨立于訓練數據集的新數據時，為了降低分類或診斷方法的誤診斷率，必須進行降維處理。AIC(Akaike Information Criterion)是一種僅依賴于訓練集信息的最優階次確定方法，故采用AIC計算降維的最優階次α，其可由AIC的最小值確定，即

(10)

式中：f(α)為將數據投影到前α個FDA向量得到的訓練集的誤診斷率。經過降維后確定一個最優判別權矩陣Wα，從而將原始數據投影到故障診斷空間，在此空間內實現故障模式的分類。

1.3 動態FDA

DFDA采用時延窗口引入時滯數據，分析變量間的時序相關特性，從而捕獲滾動軸承振動信號的周期平穩性。因此，包含當前測量變量和前d個采樣時刻測量變量的增廣變量向量為

xd(k)=[xT(k)xT(k-1) …xT(k-d)]T，

(11)

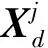
，(12)

(13)

DFDA就是對具有時滯信息的Xd進行特征值分解，獲取最優判別權矩陣。

2 基于DFDA的滾動軸承在線故障診斷方法

2.1 離線建模階段

離線建模階段的主要任務是根據所獲取的歷史振動信號建立DFDA模型。其具體步驟為：

1) 收集各種已知故障的歷史振動信號。假設包含p種不同故障類型(包括正常軸承)振動信號的一維時間序列為xj(j=1,2,…,p)，據此建立數據集。

2) 確定時延窗口d的大小，構建總體建模樣本數據集Xd。首先，提取每類振動信號的瞬時能量。在第k采樣時刻，第j類振動信號的瞬時能量ej(k)定義為

ej(k)=|xj(k)|，

(14)

則包含前d個時刻的能量特征向量Ej(k)為

Ej(k)=[ej(k)ej(k-1)…ej(k-d)]T，

(15)

最后，根據(12)和(13)式，構建維數為n×(d+1)總體數據樣本集Xd。

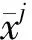
2.2 在線應用

在線故障診斷階段就是利用已經離線建好的DFDA模型實時分析滾動軸承的運行狀態。在線故障診斷過程的步驟如下：

1) 在線采集滾動軸承的振動信號x(k)(第k個采樣時刻的振動信號)，提取當前瞬時能量e(k)。根據 (15) 式構建具有時延信息的能量特征向量Enew(k)=[e(k)e(k-1)…e(k-d)]T。

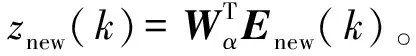
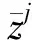
最小的歐式距離所對應的故障類別即是最終的故障決策。

4) 重復以上步驟，分析下一個采樣時刻滾動軸承的狀態。

3 應用實例與分析

3.1 振動信號采集及試驗設計

本試驗采用美國西儲大學軸承數據中心所提供的SKF6205-2RS型滾動軸承試驗數據[12]進行分析，采樣頻率為12 kHz，故障軸承的損傷直徑為0.178 8 mm，深度為0.279 4 mm。通過對健康軸承(HB)、滾動體故障軸承(BF)、內圈故障軸承(IRF)以及外圈故障軸承(ORF)分別在4種載荷條件下運行的試驗數據進行分析，以驗證所提出的在線故障診斷方法在變載荷條件下的有效性和魯棒性。其中，0%載荷條件下的試驗數據用于建立DFDA模型，每種故障樣本長度為4 800點；用50%(0.74 kW)，100%(1.47 kW)和150%(2.21 kW)負載條件下的數據作為測試樣本。在0%負載條件下，4種軸承狀態的振動信號如圖1所示。

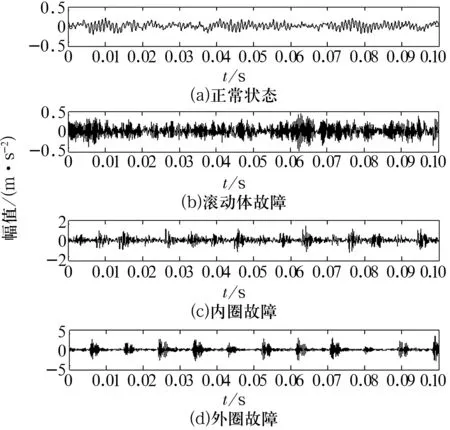
圖1 0%負載條件下4種軸承狀態的振動信號

3.2 時延窗口對故障診斷性能的影響

選取幾種不同大小的時延窗口，分別建立帶有時滯信息的DFDA模型，并對比分析建模樣本數據在各自的最佳判別空間內的可分離性，各建模樣本在判別空間的投影如圖2所示。

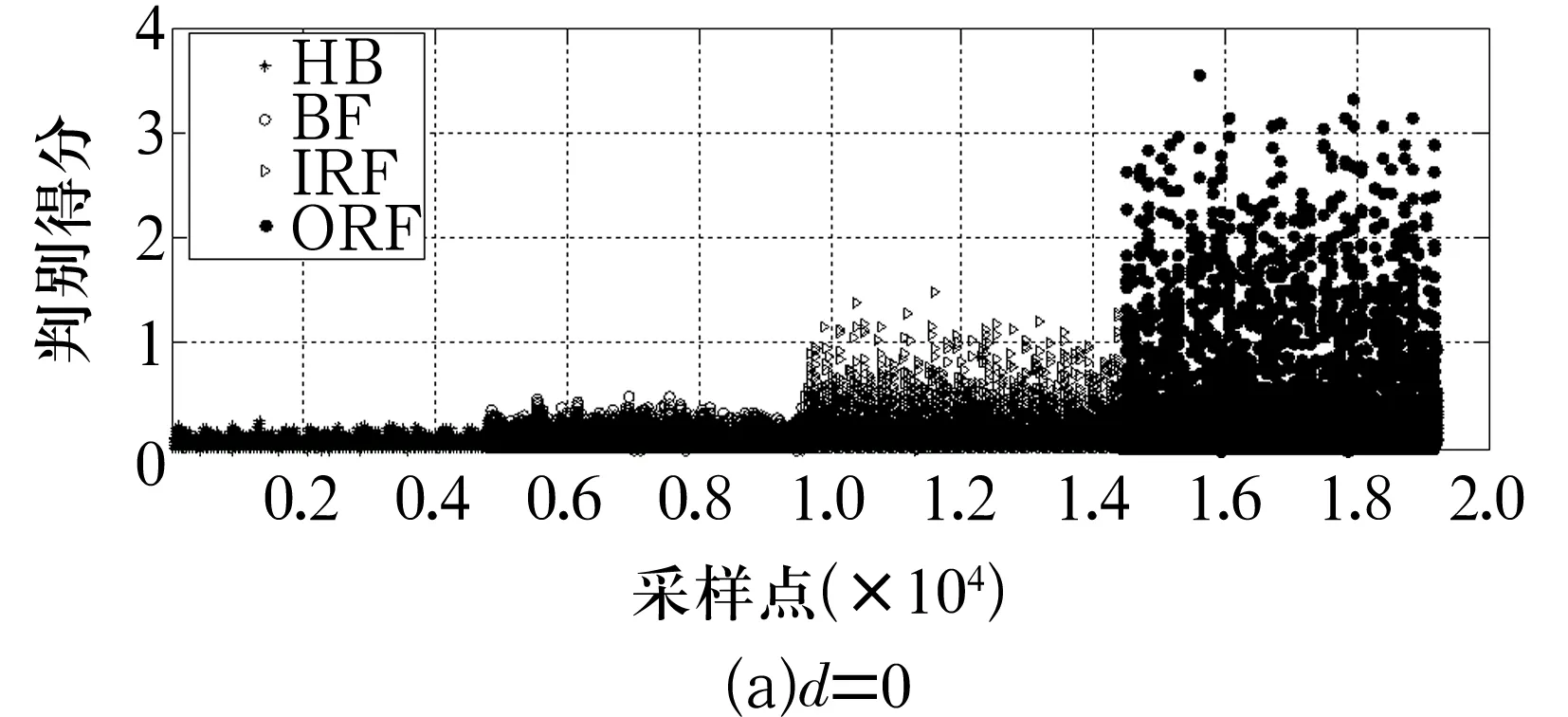
圖2 建模樣本在判別空間的投影

從圖2中可以看出：

當d取0時，建模數據中不包含過程任何動態信息，所建的DFDA模型退化為傳統的FDA模型，經FDA分析后得到了一個一維的最佳判別空間，但4種故障類型的可分性在該空間內非常差。

當d增至100時，得到一個三維的判別空間(沒有降維)，圖中的坐標分別代表運用最優判別權矩陣將原始數據投影到故障診斷空間后獲得的新的特征。由圖可知4種故障彼此之間仍存在交集。

當d=250時，得到了一個二維最佳判別空間。滾動體故障、內圈故障、外圈故障三者之間的樣本數據在此判別空間已完全分離，但正常軸承與滾動體故障仍有少量樣本存在交集。

當d分別取500和600時，都得到了一個一維的最佳判別空間，且樣本數據在這2個空間中能夠被完全分離。只是d=600時各類間的距離比d=500時的略大，故障類間的分離度略有增加。但隨著d繼續增加，故障分離度的增加并不明顯。因此，可將500作為參考設定值對延時窗口d進行設置。

另外，采用歐氏距離作為故障模式分類的判別準則，應用不同時延窗口的DFDA模型時，樣本數據故障正確識別率見表1。

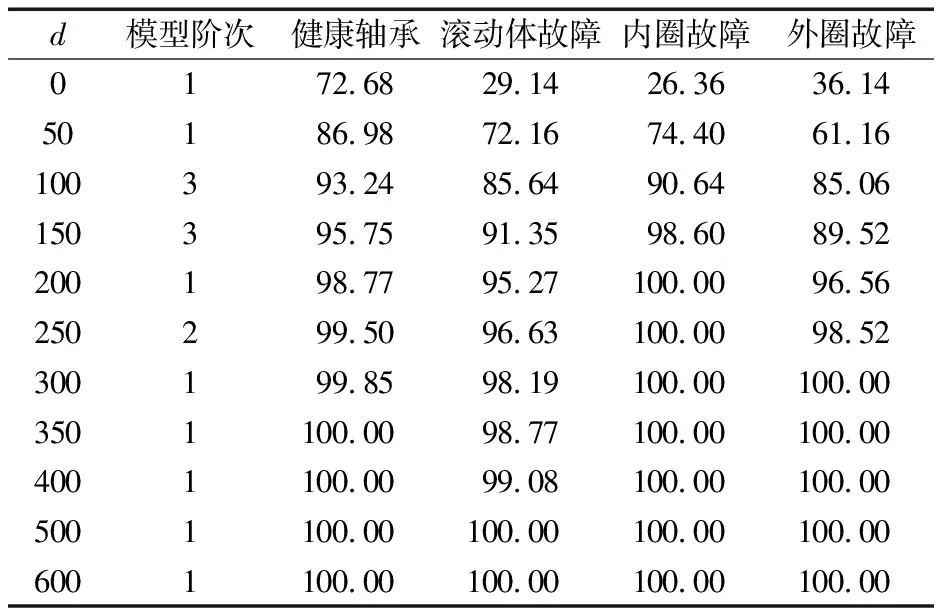
表1 不同時延窗口建模樣本的故障正確識別率

試驗結果表明：隨著時延窗口的增大，DFDA模型包含的時滯信息越多，故障類間的離散度也隨之增大，故障的可識別性提高，故障診斷的正確識別率也隨之增加。當時延窗口增至500時，所有故障樣本的正確識別率可達到100%。

3.3 變載荷條件下故障診斷性能比較與分析

為進一步分析上述故障診斷方法在變載荷條件下故障診斷能力，分別選用12 000個連續采樣的加速度信號(1 s所采集的振動信號)作為測試樣本集，在變載荷條件下運用d=300，500和600時所建立的DFDA模型進行故障診斷，結果見表2。

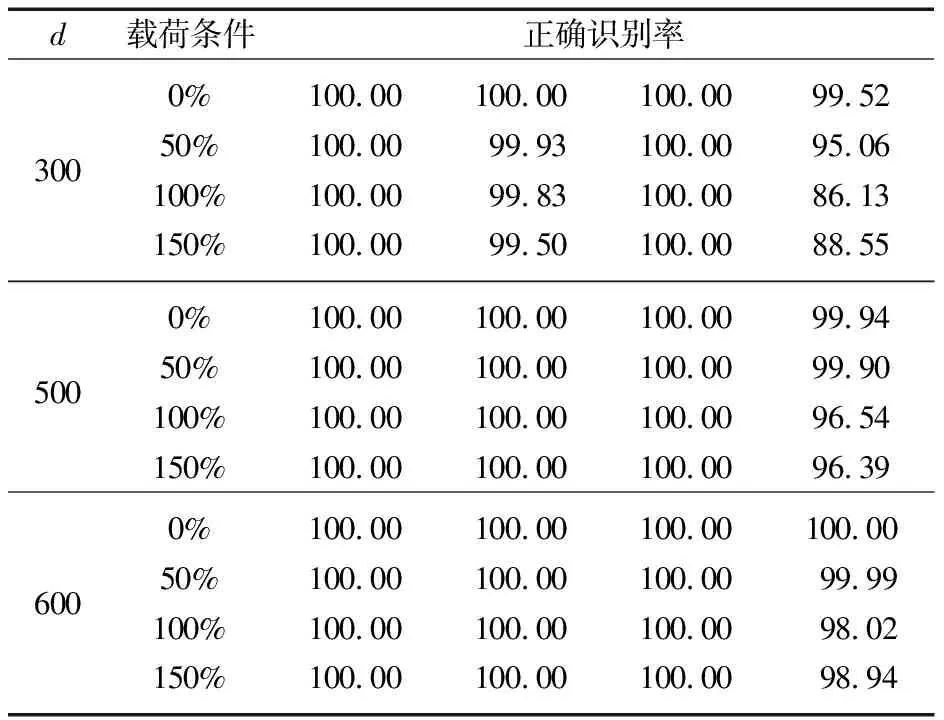
表2 不同載荷條件下故障正確識別率

由表2可知，載荷的變化對外圈故障診斷精度的影響較大，但隨著時延窗口的增加，外圈故障的識別率也隨之增加；而其他3種故障在不同時延窗口及載荷條件下的識別率均達到了100%。因此，通過設置合適的時延窗口，DFDA模型對變載荷條件的變化具有很強的魯棒性，且具有很高的診斷精度。

3.4 算法的實時性分析

仿真試驗運行環境為主頻2.8 GHz的計算機，仿真軟件為MATLAB7.1。在上述仿真環境下DFDA模型完成1次故障決策所需的時間見表3。

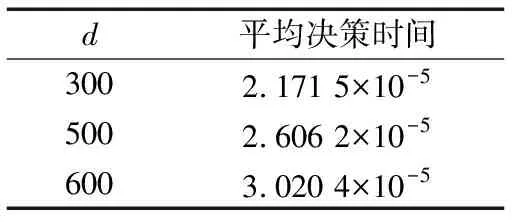
表3 不同時延窗口時的平均故障決策時間

由表3可知，盡管完成1次故障決策所需要的計算時間隨著時延窗口的增加而增加，但其計算時間均小于振動信號的采樣時間(8.333 3×10-5s)。因此，DFDA故障診斷模型的在線計算量小、診斷精度高，可以滿足在線故障診斷對實時性的要求。

4 結束語

通過引入時延窗口，DFDA故障診斷模型包含了滾動軸承運行的歷史信息，無需借助其他非平穩信號處理方法就可以有效地處理具有周期平穩特性的振動信號，解決了變載荷條件下滾動軸承故障診斷的問題，而高精度的故障診斷結果也證明了該方法的有效性以及魯棒性。

在線故障診斷時僅需調用離線建立的模型信息，在線計算量小，實時性高，更有利于實現實際工程中滾動軸承的在線故障診斷。另外，DFDA僅需當前采樣時刻及前d個采樣時刻的振動信號，即可實現每一采樣點的軸承運行狀態在線分析和診斷，有利于盡早發現故障，為維修決策爭取寶貴時間。