基于Hammerstein模型的雙閉環直流調速系統建模及參數辨識

李翠翠

【摘 要】通過借鑒“類等效”的方法建立雙閉環直流調速系統的基于傳遞函數的簡化等效模型，采用動態分離的類Hammerstein模型參數辨識方法得到其等效模型結構的參數，既能有效逼近原系統模型結構，又能觀測到飽和非線性和死區非線性等系統非線性環節的動態性能變化情況。

【關鍵詞】雙閉環直流調速 系統建模 參數辨識 Hammerstein模型 類等效

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2016）06C-0188-03

自動化生產線上的許多生產機械要求在一定的范圍內既能保證具有良好的穩態、動態性能，又能夠實現速度的平滑調節，雙閉環直流調速系統由于其調速范圍廣、靜差率小、穩定性好等特點，在電力拖動自動控制系統中被廣泛應用。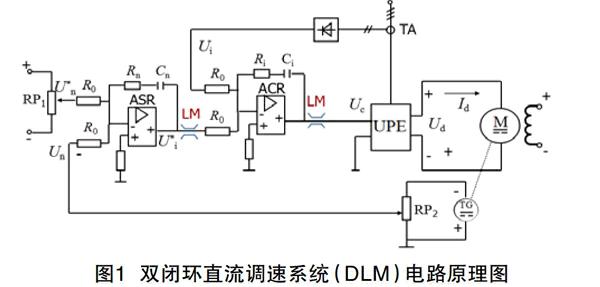

但是由于該調速系統的結構復雜，控制器的可調參數較多，使得雙閉環直流調速系統在設計和校正上存在較大的困難。雙閉環直流調速系統經過系統設計與仿真驗證，得到一個理論上的參數設置，但是應用于現場后，常常由于負載和電機勵磁變化、交流電源電壓波動、放大器輸出電壓漂移等干擾因素，導致轉速調節效果不好，運行情況與理想設計值有較大的誤差。因此為保障系統的正常運行，還需要結合現場情況進行微調，通常采用經驗法和湊試法達到穩定狀態。同時，為了更好的對該調速系統穩態和動態性能進行分析，還需要將現場湊試穩定后的系統的數學模型還原出來。

國內外學者對于雙閉環直流調速系統的建模及參數辨識進行了大量的研究，目前對DLM系統建模的方法主要有兩種：一是借鑒智能控制體系中關于復雜對象進行精確建模的“類等效”簡化建模法，這種方法通過采用各類改進的遺傳算法，對建立的雙閉環直流調速系統的非線性狀態空間模型的參數進行辨識；第二種是借助軟件模擬和數據分析建立系統模型的方法，例如有學者提出針對雙閉環直流調速系統的性能對直流電機及機械負載對象參數依賴性大的問題，提出一種基于電機機理模型的參數辨識與調節器自整定的方法；有學者提出在Matlab/xPC目標環境下使用遞推最小二乘法對某型直流電機進行參數的在線辨識，獲得某工作轉速下的動態結構圖參數，再針對該結構圖，在Simulink環境下對速度調節器和電流調節器的PI調節器參數進行整定和仿真，達到滿意效果。

本文通過借鑒“類等效”的方法建立雙閉環直流調速系統的基于傳遞函數的簡化等效模型，采用動態分離的類Hammerstein模型參數辨識方法得到其等效模型結構的參數，既能在一定程度上逼近系統模型結構，又能觀測到飽和非線性和死區非線性等系統非線性環節的動態性能變化情況。

一、雙閉環直流調速系統（DLM）的建模

（一）雙閉環直流調速系統簡介

無靜差雙閉環直流調速系統電路結構原理如圖1所示。

測速發電機TG測量電動機轉速，以電壓形式Un輸出，該轉速電壓Un與給定電壓Un*比較后得到轉速偏差△Un，經放大器放大后作為電力電子變換器的控制電壓UC，UPE輸出可控直流電壓Ud0，用以調節電機轉速，最終使得電機轉速與設定速度一致。

同時，引入電流截止負反饋ACR來限制動態過程的沖擊電流；轉速電壓、電流與給定電壓、電流的比較和放大環節使用輸出帶有限幅的PI調節器以獲得良好的靜、動態特性。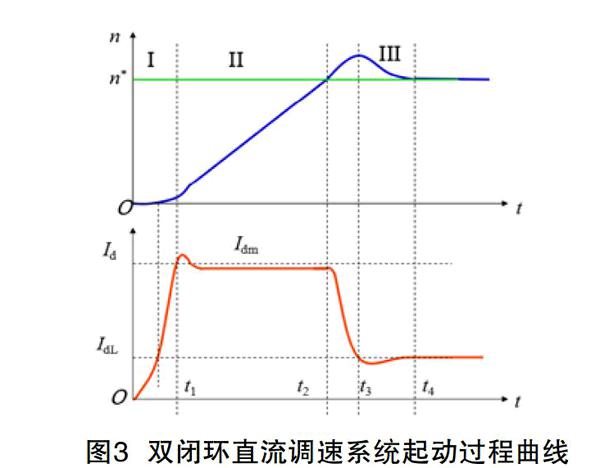

（二）雙閉環直流調速系統的數學建模

根據系統的工作原理以及圖1各個環節輸入輸出之間的關系，計算雙閉環直流調速系統各模塊的傳遞函數，其中：

轉速調節器ASR：

電流調節器ACR：

檢測環節中直流閉環調速系統的測速反饋環節和電流截止負反饋環節的響應都可以認為是瞬時的，因此這兩個環節的傳遞函數就是它們的放大倍數，即測速裝置電壓放大倍數為α，電流檢測裝置電流放大倍數為β。

連接各個環節的傳遞函數表達式，得到該系統的動態結構框圖，如圖2所示：

（三）基于“類等效”的DLM系統結構框圖等效化簡

要對雙閉環直流調速系統的結構圖進行等效化簡，必須先熟悉其起動過程，圖3所示為雙閉環直流調速系統的起動過程曲線：

目前有研究成果詳細介紹了該系統起動過程中轉速調節器ASR和電流調節器ACR的工作原理。基于“類等效”模型簡化的方法，在第I階段，即電流上升（0-t1）時間段，由于其電流變化迅速，使得整個過程時間非常短，轉速變化不大，因此我們把這一階段的影響忽略不計；在第II階段，即恒流升速（t1-t2）時間段，ASR始終在飽和狀態，轉速調節器相當于開環，ACR起主要調節作用，不應飽和，為使轉速和電流呈線性增長，可以把系統中電機與電流環等效為一個積分環節，并設積分時間常數為T2；第III階段，即轉速調節（t2以后）時間段，ASR退出飽和，起主導調節作用，轉速仍然上升至t-t3時達到峰值，此后減速直至穩定，而轉速調節器ACR則作為一個電流隨動子系統，力圖使Id盡快地跟隨其給定值Ui*。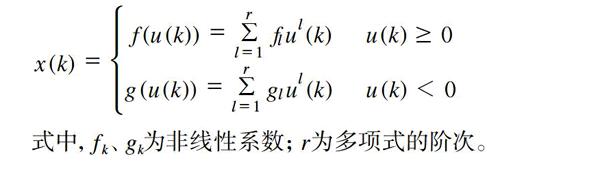

通過以上的分析看出，轉速調節器經歷了不飽和—飽和—退出飽和三個狀態，考慮采用一個比例、積分和飽和非線性環節來等效表示WASR。設比例系數為K，積分時間常數T1，飽和非線性環節的線性域寬度為，則雙閉環調速系統的動態結構圖可以簡化等效為圖4：

根據系統的結構框圖，可以得到輸入為控制電壓Un*，輸出為電機轉速n（r/min）的雙閉環直流調速系統等效線性模型為一個二階線性系統，其傳遞函數為：

（四）DLM系統的非線性模型分析

等效模型的傳遞函數計算中并沒有涉及ASR的飽和非線性環節。

而在本文簡化等效的雙閉環直流調速系統中，為將轉速調節階段時的ASR限制在不飽和狀態，要求轉速調節器的輸出Ui*必須滿足： ，即存在飽和非線性環節。

同時，在進行轉速測量時，測速發電機的輸出電壓與輸入轉速應該成正比，但是若遇到電刷壓降的情況，則只有在轉速超過一定值之后才會有電壓輸出，導致了一定的電壓、轉速關系的死區。

在傳遞函數式所滿足的線性模型的基礎上，加入非線性環節（不飽和限制、死區誤差），就得到了包含線性和非線性特性的整體控制對象模型，如圖5。該模型可以用分段多項式類Hammerstein模型進行描述，通過動態分離辨識算法實現系統線性和非線性部分解耦辨識，特別是重構出中間信號Ui*，可以觀測雙閉環調速系統轉速調節階段輸出電壓飽和非線性的非飽和區動態變化。

二、基于Hammerstein模型的DLM系統參數辨識方法

從前一部分的分析可以看出，雙閉環直流調速系統中即包含串聯結構的非線性因素，又包含反饋結構的非線性因素，因此不能以簡單的線性模型進行等效。從線性動力學、死區非線性誤差以及飽和非線性的作用順序上，可將雙閉環直流調速系統在結構上大致等效為靜態非線性模塊在前，動態線性模塊在后的串聯結構，這樣就可以利用Hammerstein模型結構特性，通過單一的輸入輸出信號實現對系統線性和非線性參數的辨識。同時，通過辨識后獲得的中間信號可等效于系統ASR的輸出-電機與電流環的輸入信號，以區分系統的線性和非線性特性，從而達到對線性和非線性模型進行解耦的目的。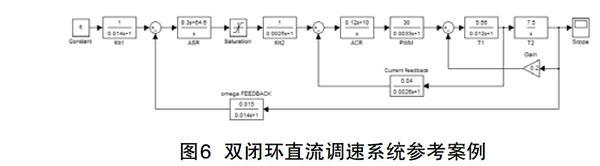

Hammerstein模型中的線性部分表示如下：

考慮到飽和非線性和死區非線性在系統中存在非對稱特性，Hammerstein模型中的非線性部分采用分段多項式函數來表示，非線性部分的輸入輸出關系為：

式中，fk、gk為非線性系數；r為多項式的階次。

定義分段函數

中間信號x（t）可以寫為：

考慮典型情況，取b0=0，整理成線性回歸的形式，即：

其中回歸向量 和待估計參數向量如下：

的中間輸入變量x（k）是不可測量的值，采用迭代過程進行估計。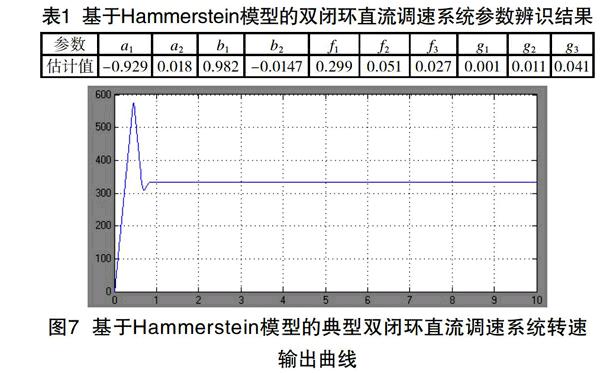

三、實驗與仿真

以圖6所示的雙閉環直流調速系統為參考案例，根據穩定系統特性，為便于觀察響應的過渡過程，輸入信號Ui*=5V，非線性環節電流限幅值為8A。

運行之后，數據通過Scope傳遞到工作空間，根據等效，該系統變換為Hammertein模型結構中的線性階次na=2，nb=2。為了計算簡便，取非線性部分多項式階次r=3，采用最小二乘迭代算法，得到Hammerstein模型線性部分的參數估計值見表1，同時得到等效Hammerstein模型的輸出轉速和電流見圖7、8。仿真結果表明，采用Hammerstein模型的非線性辨識方法具備一定的系統辨識精度，可以為雙閉環直流調速系統控制器的設計提供可靠依據。

本文針對雙閉環直流調速系統中的線性部分和飽和非線性特性，分別進行了建模和分析，借鑒“類等效”的思想，將電流調節器等效為一個比例、積分和飽和非線性環節，經過化簡提出了使用基于分段多項式的Hammerstein模型來等效雙閉環直流調速系統的思路，實驗中將等效的H系統的線性和非線性特性進行了動態分離，并采用迭代最小二乘法對非線性模型參數進行了估計。仿真結果表明，采用Hammerstein模型的非線性辨識方法具備一定的系統辨識精度，可以為雙閉環直流調速系統控制器的設計提供可靠依據。

【參考文獻】

[1]陳伯時.電力拖動自動控制系統-運動控制系統[M].北京：機械工業出版社，2005

[2]劉春艷，聞玉鳳.基于MATLAB/Simulink雙閉環直流調速系統的仿真研究[J].山西大同大學學報（自然科學版），2014（30）

[3]邵雪卷，張井岡，趙志誠.雙閉環直流調速系統的飽和限幅問題[J].電氣電子教學學報，2009（31）

[4]李永龍，李祖樞，王牛.直流電機雙閉環調速系統（DLM）的建模與辨識[J].控制理論及應用，2008（25）

[5]鄭忠杰，陳德傳.基于對象參數辨識的直流雙閉環調速系統[J].杭州電子科技大學學報，2012（32）

[6]王建鋒，張天宏.基于Matlab/xPC的直流電機參數辨識及雙閉環控制研究[J].測控技術，2011（30）

[7]高建強，姜磊.基于遺傳算法的雙閉環直流調速系統設計[J].微計算機信息，2011（4）

[8]曹立，李訓龍.Hammerstein模型辨識的回顧及展望[J].控制理論與應用，2014（31）

[9]譚力寧，韓海濤，馬紅光，蘆利斌，金國棟.基于并聯Hammerstein模型的無刷電機辨識[J].信息與控制，2013（42）

（責編 丁 夢）