滴定分析模型的統一、MATLAB解析及曲線繪制
孫曉波 李 琳 王秀霞 王進平
(青島農業大學化學與藥學院,山東青島266109)
?
滴定分析模型的統一、MATLAB解析及曲線繪制
孫曉波李琳王秀霞王進平*
(青島農業大學化學與藥學院,山東青島266109)
摘要:在將酸堿滴定、絡合滴定、氧化還原滴定和沉淀滴定反應統一為M+L=N的基礎上,將4種滴定曲線方程統一為兩種數學模型。通過簡單迭代法計算滴定過程中變化的副反應系數,利用接近數學表達式的自然化語言MATLAB解析4種滴定曲線方程,并繪制出精確的滴定曲線,方法簡單易操作。
關鍵詞:滴定曲線;MATLAB;模型統一
酸堿滴定、絡合滴定、氧化還原滴定和沉淀滴定是分析化學中化學分析的核心內容[1]。雖然4種滴定反應的本質不同,且可能伴隨著各種副反應,滴定過程較為復雜,但是利用林邦的副反應思想均可以將這4種滴定反應統一為M+L=N[1-4]。在此基礎上,可以將這4種滴定曲線統一為兩種數學模型。模型的統一可以使學生更好地理解滴定分析的原理和本質。同時,目前計算機技術的快速發展為解析這些復雜的分析化學模型提供了可能。尤其是MATLAB軟件能夠提供高效的數值計算功能,能使用戶從繁雜的數學運算分析中解脫出來;特別是其友好的用戶界面及接近數學表達式的自然化語言,使用戶易于學習和掌握;而且具有完備的圖形處理功能,實現計算結果和編程的可視化。它應該是化學工作者解析復雜的滴定分析模型的強有力的工具。因此,本文在統一4種滴定分析數學模型的基礎上,利用MATLAB軟件解析滴定曲線方程模型,并繪制滴定曲線。
1 酸堿滴定和沉淀滴定模型
以標準NaOH溶液滴定HCl及Cl-滴定Ag+為例,滴定反應分別為:
酸堿滴定:H++OH-=H2O
沉淀滴定:Ag++Cl-=AgCl
酸堿滴定及沉淀滴定反應可統一為:
M+L=N
其中M分別代表H+和Ag+,L分別代表OH-和Cl-,N分別代表HO和AgCl。在酸堿滴定和沉淀滴定
2反應中N為純水和沉淀,[N]=1。因此,考慮到體積變化,兩種滴定曲線方程可以統一為[1,5]:
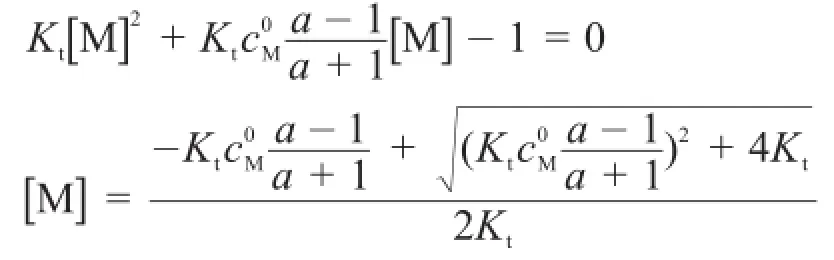
滴定常數Kt表示滴定反應進行的程度,在酸堿滴定中為Kt=1/Kw=1014,而在沉淀滴定中為Kt=1/Ksp。滴定分數a=cM/cL。
當不考慮副反應時,利用MATLAB可以非常容易地解析方程并繪制滴定曲線,程序如下:
a=0:0.001:2;
Kt=10^14;
C0=0.1
d=(a-1)./(a+1);
b=Kt*C0*d;
e=b.^2;
g=sqrt(e+4*Kt);
M=(-b+g)./(2*Kt);
pH=-log10(M)
plot(a,pM,'.')
將1/Kw=1014,1/Ksp=109.75、1012.31、1016.08分別賦值于Kt,即可繪制出0.1mol·L-1NaOH滴定0.1mol·L-1HCl的酸堿滴定曲線,以及0.1 mol·L-1Cl-、Br-、I-分別滴定0.1 mol·L-1Ag+的沉淀滴定曲線(圖1)。
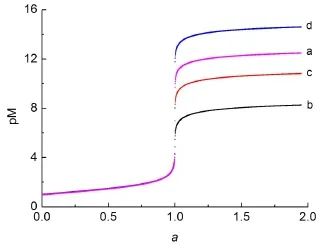
圖1 利用統一模型繪制的酸堿滴定曲線與沉淀滴定曲線
在統一模型中強酸堿滴定與沉淀滴定唯一的差異是Kt,而將1/Kw及不同的1/Ksp賦值于Kt,即可繪制與文獻[1,5,6]理論計算結果相一致的滴定曲線。
當強堿滴定弱酸時,由林邦副反應思想,強堿滴定弱酸的反應式可以寫為:
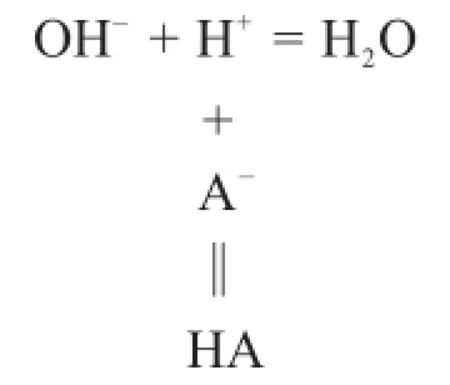
則條件滴定常數為:
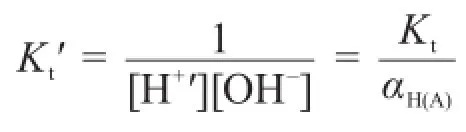
考慮體積變化:
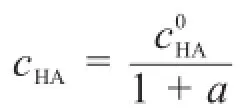
其中cHA為滴定過程中弱酸濃度,[H+?]為未參與中和反應的質子的總濃度。式中αH(A)為質子的副反應系數,為弱酸的原始濃度。
根據林邦副反應思想,將Kt?代入到強堿滴定強酸的滴定曲線方程[3,4],得強堿滴定弱酸的滴定曲線方程為:
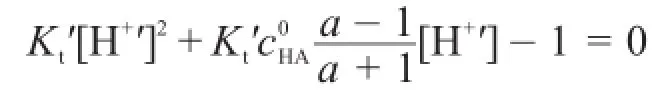
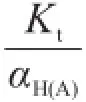
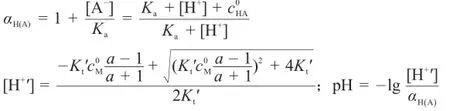
由于副反應系數αH(A)隨滴定過程而變化,因此解析該滴定曲線方程較為復雜。本文利用一個簡單的迭代:
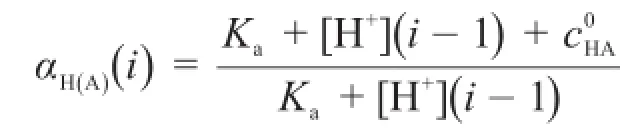
很容易解決了αH(A)隨滴定過程變化的問題,準確地繪制了強堿滴定弱酸的滴定曲線。
利用MATLAB解析該方程并繪制滴定曲線程序如下:
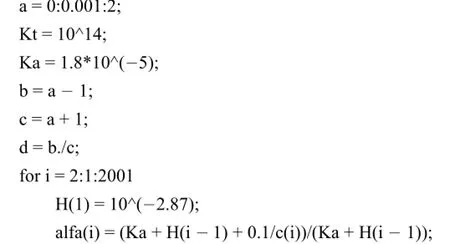

由圖2(A)可以看出,其滴定突躍范圍與文獻[1]中的結果相一致,表明該模型能夠準確繪制出強堿滴定弱酸時的滴定曲線,且無需解復雜的一元三次方程[5]。另外,將10-3、10-5、10-7、10-9、10-11分別賦值于Ka,可以非常容易地繪制出強堿滴定不同弱酸的滴定曲線(圖2(B))。

圖2 利用統一模型繪制的NaOH滴定不同弱酸的滴定曲線
2 絡合滴定和氧化還原滴定模型
對于氧化還原反應,采用林邦副反應思想,把一個半反應看作是另一個半反應的副反應,便可和絡合滴定反應統一為M+L=N。其中L可為Y或e-。而滴定曲線方程統一為[1,5]:
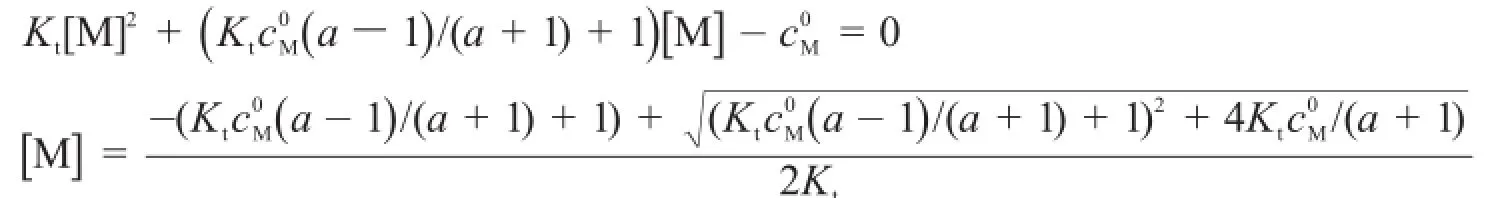
以0.01 mol·L-1Y滴定0.01 mol·L-1的Ca2+為例,利用MATLAB解析該方程并繪制滴定曲線,程序如下:
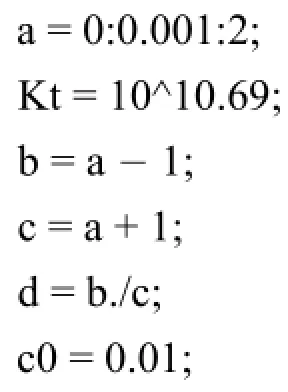

由圖3可以讀出EDTA滴定Ca2+的突躍范圍為(5.299,7.692),與文獻[7]結果相一致。因此利用統一的滴定模型能夠準確繪制出絡合滴定曲線。將不同K?MY賦值給Kt,賦予cM0不同的初始濃度,則分別得到絡合滴定曲線(圖4)。
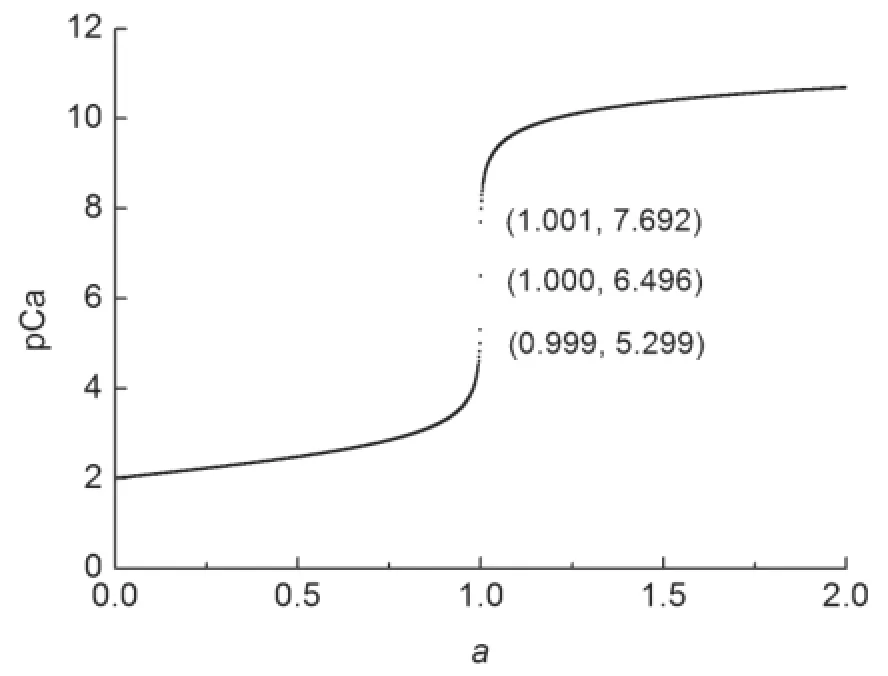
圖3 利用統一模型繪制的EDTA滴定Ca2+的滴定曲線
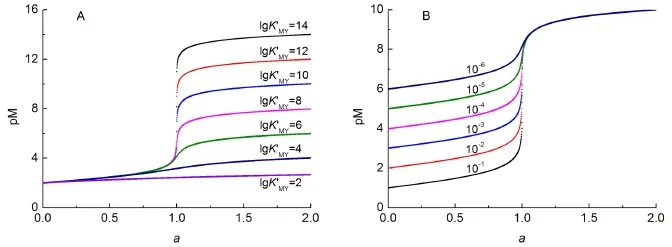
圖4 在不同的K′MY(A)及cM0(B)時,利用統一模型繪制的EDTA絡合滴定曲線
氧化還原滴定時,以Ce4+滴定Fe2+為例:
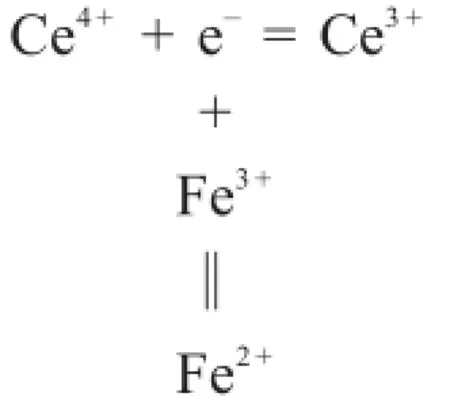
主反應常數為:
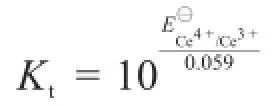
不考慮副反應時,滴定曲線方程為:
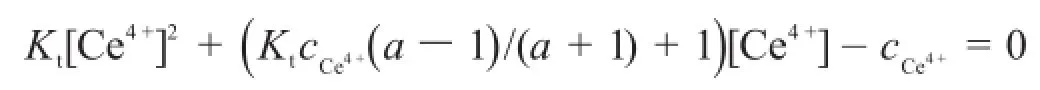
或
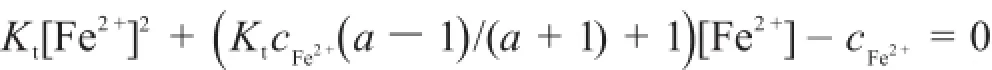
考慮副反應時,有:
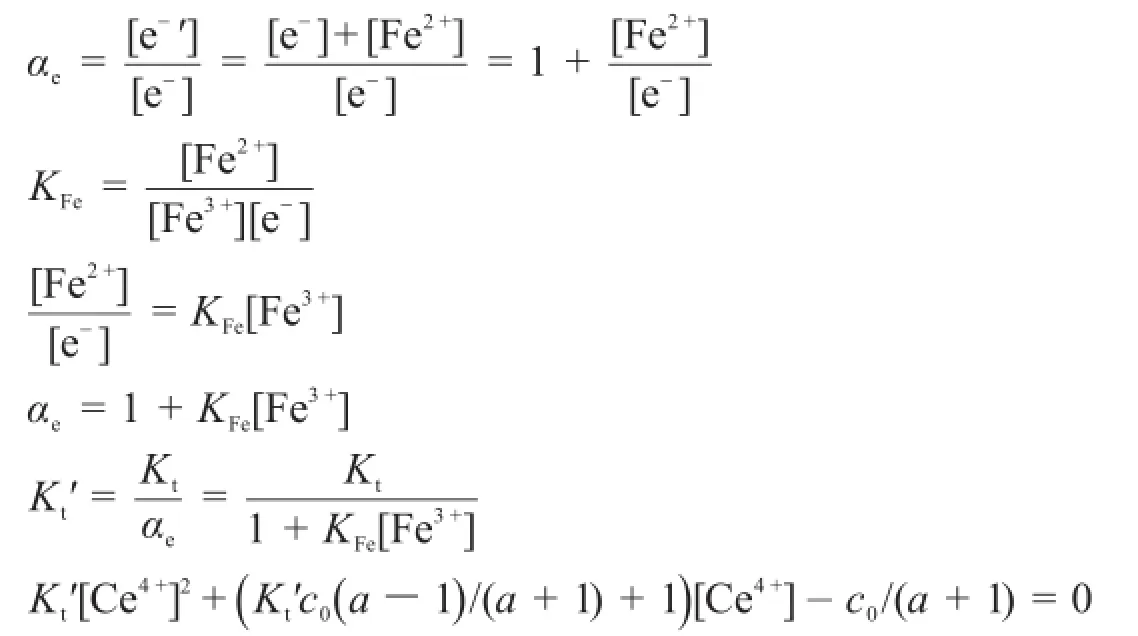
或
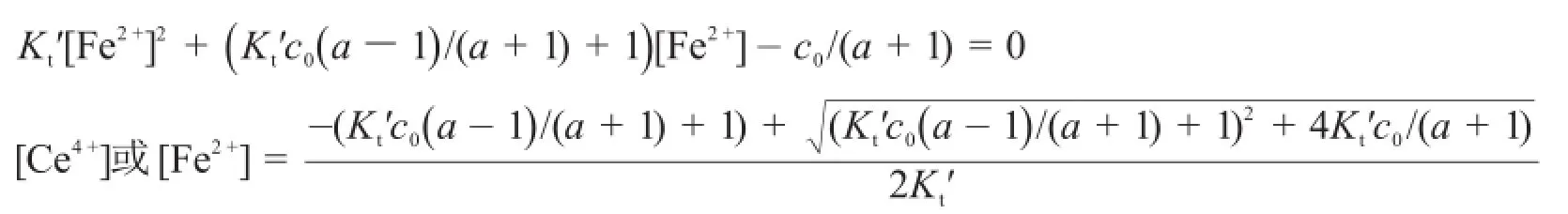
由于副反應系數αe隨滴定過程[Fe3+]的變化而變化,因此解析該滴定曲線方程較為復雜。本文利用一個簡單的迭代αe(i)=1+KFe[Fe3+](i),計算出變化的αe。利用MATLAB則能夠準確地解析滴定曲線方程,并繪制了滴定曲線,程序如下:


所繪制的Ce4+與Fe2+相互滴定的滴定曲線如圖5所示,可以看出由統一模型所繪制的曲線與文獻[1,5]的理論計算結果相一致。
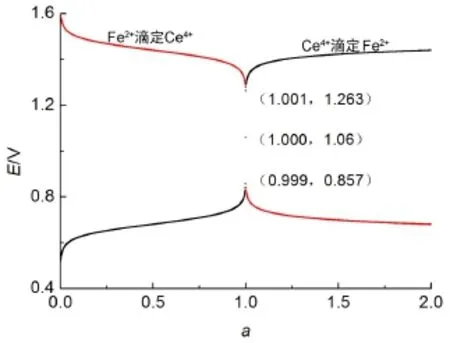
圖5 利用統一模型繪制的氧化還原滴定曲線
3結論
參考文獻
[1]武漢大學.分析化學(上冊).第5版.北京:高等教育出版社,2006.
[2]梁保安.許昌學院學報,2003,22(5),31.
[3]喬成立,丁言偉.高師理科學刊,2003,23(4),46.
[4]孟凡昌,楊代菱.大學化學,2001,16(4),30.
[5]王進平,孫曉波.大學化學,2014,29(6),29.
[6]李克安.分析化學教程.北京:北京大學出版社,2009.
[7]賈之慎.無機及分析化學.北京:中國農業大學出版社,2009.
中圖分類號:O6;G64
doi:10.3866/PKU.DXHX201505015
*通訊作者,Email:jpwang@qau.edu.cn
基金資助:山東省高等學校精品課程(2013BK205);山東省高等教育應用型人才培養特色名校建設項目
A Universal Model for Titrations and Titration Curves Constructed Using MATLAB
SUN Xiao-BoLI LinWANG Xiu-XiaWANG Jin-Ping*
(College of Chemistry and Pharmaceutical Sciences,Qingdao Agricultural University,Qingdao 266109,Shandong Province,P.R.China)
Abstract:In this article,the reactions for acid-base,complexometric,redox and precipitate titrations can be generalized as M+L=N.Accordingly,their titration curve functions can be expressed as two mathematical models.MATLAB was used to analyze the titration curve models.The changing side reaction coefficients in titration process were calculated by a simple iteration method.Finally,the exact titration curves were plotted using this facile method.
Key Words:Titration curves;MATLAB;Universal model

