不拘一格有妙招
余亞明
【摘要】在學生已有認知經驗的基礎上,教師根據題型的具體特征,引導學生嘗試突破常規的解法,歸納方法和技巧,讓學生感受成功。
【關鍵詞】靈活變式探究生成提升能力
數學離不開解題,但解題教學時不應該只重視教會學生一招一式,讓學生習慣于所謂的“標準”解法,而應該重視對知識的靈活應用,鼓勵學生不斷地去探索新的解法,長此以往,學生就能隨機應變,從而提高思維能力和創新能力。下面結合教學實際舉例談談幾種突破常規的數學解題方法。
一、 “目標轉移”法
例1如圖1,已知菱形ABCD,CE、CF分別垂直于AB、AD,垂足為E、F。求證:CE=CF。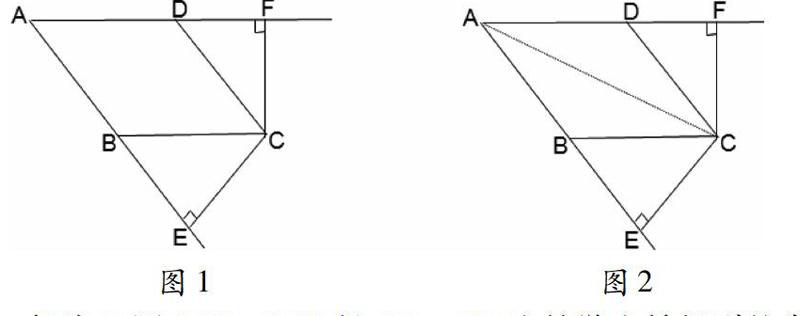
解法1:證BCE≌DCF得CE=CF,這是學生易想到的常規解法。
解法2:轉移目標,讓學生聯想菱形對角線的性質,如圖2,連結AC,不難得到AC平分∠BAD, 又CE、CF分別垂直于AB、AD,垂足為E、F,利用角平分線的性質可迅速得到CE=CF。
解法3:轉移目標,讓學生聯想菱形面積的計算方法,可得出
S菱形ABCD=AB·CE,S菱形ABCD=AD·CF,又AB=AD, 從而得到CE=CF。
很明顯,后兩種解法比較簡單,不僅改變了學生通過三角形全等來證明結論的習慣,也讓學生對菱形的性質有了更深刻的認識,有利于學生溝通知識間的縱橫聯系。
二、 “一反常態”法
例2計算:(2-1)(2+2)
解法1:原式=2×2+2×2-1×2-1×2=22+2-2-2=22-2=2;該常規解法是運用多項式乘以多項式的法則進行解題。
解法2:觀察到2+2=2(2+1),故本題就可以采用以下解法:
原式=(2-1)·2·(2+1)=(2-1)·(2+1)·2=2。
后一種解法改變了固有計算的模式,巧妙地將2+2進行了分解,從而簡化了運算的過程,也提高了學生的思維水平。
例3已知方程組2x+3y=11
3x+2y=4,則x+y=。
解法1(常規解法):利用加減消元或代入消元法解方程組,得到x=-2,y=5,再計算x+y=3。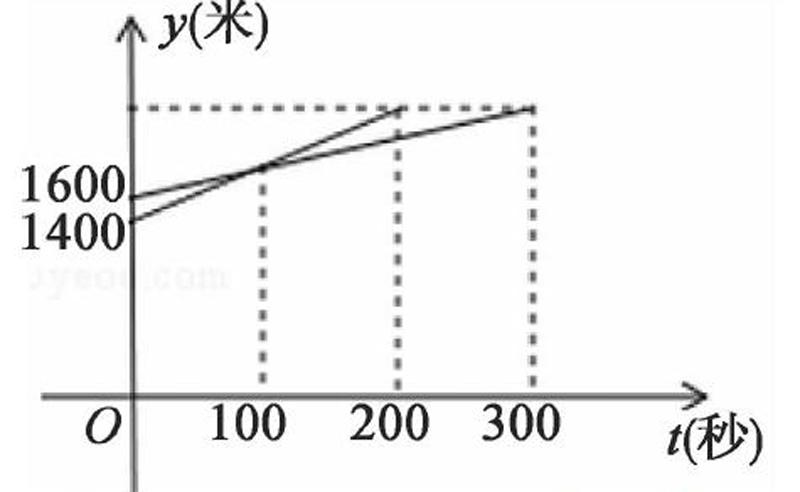
解法2:將原方程組中兩個方程相加得5x+5y=15,再把所得方程兩邊除以5得x+y=3。
三、 “去偽求真”法
例4如圖3,在ABCD中,E、F分別是邊AB、CD上的點,已知AE=CF,M、N是DE和FB的中點。求證:四邊形ENFM是平行四邊形。
解法1(常規解法):證ADE≌CBF得DE=BF,∠AED=∠CFB,再由中點條件得EM=NF,由ABDC得∠AED=∠CDE,等量代換得∠CFB=∠CDE,從而DEBF即EMNF,證得四邊形ENFM是平行四邊。(甚至有學生證兩次全等,此處略過。)
解法2:引導學生去掉無用的線條,分析出BEDF且BE=DF可得四邊形EBFD是平行四邊形,再結合中點條件,學生易得四邊形ENFM是平行四邊形。
后一種解法去掉了不需要用的線條(“去偽”),抓住要證的,把與問題有關的圖形抽象出來(“求真”),輕松解決問題。
四、 “貼近實際”法
例5一次越野跑中,當小明跑了1600米時,小剛跑了1400米,小明、小剛在此后所跑的路程y(米)與時間t(秒)之間的函數關系如圖6,則這次越野跑的全程為米。
解法1(常規解法):結合圖像設兩條直線的解析式為:y小明=k1x+1600,y小剛=k2x+1400,當x=100時,y小明=y小剛, 當x=300時的y小明與當x=200時的y小剛相等,100k1+1600=100k2+1400
300k1+1600=200k2+1400,解得k1=2
k2=4,故這次越野跑的全程為:1600+300×2=2200米。(此方法與設兩人速度列方程組的方法相同,此處略去。)
解法2:由圖像中兩線交點的實際意義可知:100秒的時間內小剛比小明多走了200米,說明小剛每秒比小明多走2米;再結合兩線交點及兩線的末端可知:小剛用100秒(200-100)走的路程和小明用200秒(300-100)走的路程,說明小剛的速度是小明的2倍。故小剛的速度是每秒4米,小明的速度是每秒2米, 最終得出全程2200米。
兩種解法本質上是相同的,只是理解的角度不同,筆者在教學時,發現學生更傾向于后種解法,認為更貼近自己的生活實際,實踐說明,后種解法更方便、更省時。
五、 “他山之石”法
例6如果關于x的方程|x-1|+|x+1|=k有實根,則實數k的取值范圍是()。
A. k≥0B. k>0C. k≥2D. k≥1
解法1:(1) 當x≥1時,k=|x-1|+|x+1|=x-1+x+1=2x≥2;
(2) 當x≤-1時,k=|x-1|+|x+1|=1-x-x-1=-2x≥2;
(3) 當-1≤x≤1時,k=|x-1|+|x+1|=1-x+x+1=2;
該常規解法需要分類討論,而且學生極易發生錯誤。
解法2:聯系數軸, 如圖7,把數軸上表示-1、1的點記著點A、B,設實數x對應數軸上的動點P,由絕對值的幾何意義可知:
PB+PA=|x-1|+|x+1|
當點P在點A的左側以及點P在點B的右側時,PA+PB>AB。
當點P在點A、B之間時,PA+PB=AB
故PA+PB≥AB即PA+PB≥2,又因為方程|x-1|+|x+1|=k有實數根,所以選C。
后一種解法用從幾何的角度解決了代數問題,更形象更直觀,學生易于理解。
例7點(x,2-x)不可能在第幾象限?
解法1(常規解法):分類考慮x是正數、0、負數三種不同情形時,得到的點的坐標情況,解決過程較煩瑣。
解法2:設y=-x+2,易得函數y=-x+2的圖像分布在第一、二、四象限,所以點(x,2-x)不可能在第三象限。
后一種解法避開了繁雜的分類討論,巧妙地用函數解決了坐標問題。
以上是筆者在教學實踐中的一點嘗試。題海茫茫,千變萬化,只有不斷地總結解題方法,在總結中反思,在總結中比較,才能在總結中提升。從而提高學生的學習積極性,拓寬學生的思維空間,提高教育教學水平。

