基于Copula函數不同季度上證指數的相關性分析

姜瑩瑩，劉文瓊

（湖州師范學院理學院，浙江湖州313000）

基于Copula函數不同季度上證指數的相關性分析

姜瑩瑩，劉文瓊

（湖州師范學院理學院，浙江湖州313000）

借鑒Copula函數在尾部相關性研究的應用理論，建立Copula函數模型，對不同季度上證指數的尾部相關性進行研究，并利用上證指數進行實證分析.結果顯示，各季度收盤價間有正尾部相關性.尾部相關性研究為風險量化管理提供了一種新途徑.

Copula函數；最優函數；尾部相關性；上證指數

MSC 2010：91G70

0 引言

股票市場中，一支股票產生劇烈動蕩時，往往另外幾支股票也會受到影響.在全球經濟一體化形勢下，這樣的趨勢日益加強，影響范圍更加廣泛，其程度也更加嚴重.因此，研究股票市場間的聯系甚至量化它們的相關關系，增強股市穩定性，減少投資損失，就顯得十分重要.相關性分析在金融市場相關結構的定量分析中占有重要地位.風險的度量、資產的定價以及如何選擇投資組合等問題都可利用相關性方法進行分析.尾部相關性分析為其中一種，它是通過尾部相關系數對變量進行分析的.對不同時段的股價進行尾部相關性分析，可得到不同時段之間的相關性規律，由此就可按照近期數據定量地推測遠期的股價，從而形成短期預測.

在相關性分析中，Copula理論應用較為廣泛.Copula理論最早由Sklar提出，它克服了用線性相關指標度量相關性存在的局限性，反映了變量間的相關性［1］.Copula函數理論多應用在風險管理方向、資產收益建模和信用評級等方面.在金融數量分析中，Romano利用Copula方法對意大利的股票收益率進行了相關性分析［1］；劉國光等［2］利用Copula理論探討了深圳A股和B股投資組合的風險性等.在航班延誤［3］、投資組合風險價值［4］等方面，Copula理論也有廣泛應用.

針對現有的Copula理論尚未對單個變量在不同時段的相關性進行研究的不足，本文采用Copula函數方法代替線性相關系數，選擇最優函數描述上證指數在不同季度的相關性及尾部相關性.

1 Copula函數的定義

Copula函數最早是由Sklar提出的.他指出，Copula函數可把多個隨機變量的聯合分布與其各自的邊緣分布連接起來，因此Copula函數又被稱作“連接函數”或“相依函數”［1］.

1.1 Copula函數的定義與基本性質

Copula函數的一般性定義由Nelsen（1998）給出［5］：N元Copula函數C滿足以下條件：①C的定義域為IN=［0，1］N；②C是N維遞增的、有界的；③C的邊緣分布函數Cn滿足Cn（u）= C（ 1，1，…，u，1，…，1）=u，其中，u∈［0，1］，n=1，2，...，N.

由以上定義可知，若有N維隨機向量（x1，x2，...，xN），F1，F2，...，FN為x1，x2，...，xN連續的邊緣分布函數，其聯合分布函數是F（ x1，x2，...，xN），隨機向量的Copula函數為C，則N維隨機向量的聯合分布滿足：

1.2 Sklar定理［6］

設F，G是隨機變量X，Y的連續邊緣分布函數，其聯合分布函數為H，則存在唯一對應的Copula函數C（C在range F×range G上唯一確定），對任意的（x，y）∈R2，都有：

H（x，y）=C（F（x），G（y））.

相對應地，對于任意的兩個邊際分布函數F（x）、G（y）和一個Copula函數C，則由上式定義的分布函數H（x，y）是一個以F，G為邊際的聯合分布函數.

由Sklar定理可知，通過Copula函數可將邊緣分布和變量間的相關結構分開研究，由此可掌握金融市場的真實相關性.此外，還可利用Copula函數導出的相關性測度捕捉隨機變量間的非對稱相關性，研究分布的尾部相關性.

2 函數的選擇與相關性測度

2.1 Copula函數的估計與選擇

為了避免由于邊緣分布函數的設定誤差而產生Copula函數的有偏估計，本文采用τ統計量估計Copula函數［5］，并選擇了單參數的阿基米德Copula函數，包括Gum bel、Frank、FGM、Clayton函數，即C=｛Clayton，Frank，FGM，Gumbel｝.各函數的τ統計量都是關于Copula函數中參數θ的函數，由此可以估計出參數θ的值.設隨機變量為x，y，Copula函數的表達式如下.

2.1.1 Copula函數的估計

①Gumbel Copula函數：記Gumbel Copula函數為CG，其表達式及τ統計量分別為：

θ越大，表示兩個變量的尾部相關性就越高.當θ=1時，說明x，y獨立，CG=xy；當θ趨于∞時，x，y趨于完全相關.

②FGM Copula函數：記FGM Copula函數為CFGM，其表達式及τ統計量分別為：

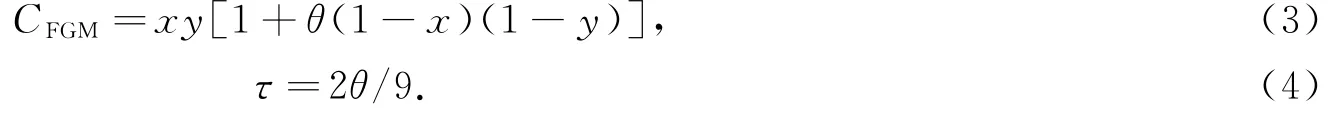
當θ＜0時，說明x，y呈負相關關系；當θ＞0時，說明x，y呈正相關關系.

③Frank Copula函數：記Frank Copula函數為CF，其表達式及τ統計量分別為：

當θ＜0時，說明x，y呈負相關關系；當θ趨于0時，說明x，y趨于相互獨立；當θ＞0時，說明x，y呈正相關關系.

④Clayton Copula函數：記Clayton Copula函數為CC，其表達式及τ統計量分別為：

當θ趨于0時，表示x，y趨于獨立；當θ趨于∞時，表示x，y趨于完全相關.

2.1.2 Copula函數的選擇

為了使利用Copula函數描繪的不同股票市場數據之間的相關性結構達到最佳效果，本文選擇與經驗Copula函數之間誤差最小的理論的Copula函數［8］.

理論的Copula函數即用τ估計的Copula函數，記為C，C=｛Gumbel，FGM，Frank，Clayton｝.經驗的Copula函數是由Deheuvels提出的［6］.假設一組樣本為：（x1，y1），（x2，y2），…，（xn，yn），其中，n為樣本容量，則二元經驗的Copula函數為：

其中：

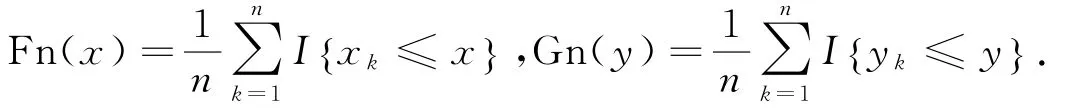
對于二元的Copula函數，本文把用τ估計出來的Copula函數稱為理論的Copula函數，記作C（ u1，u2），對應的經驗的Copula函數記作C^（u1，u2）.記最優的Copula函數為C*，則滿足以下條件：

即選擇與經驗的Copula函數之間的誤差最小的函數.

2.2 尾部相關性

尾部相關性是通過尾部相關系數進行分析的.尾部相關系數廣泛應用于極值理論，反映當一個變量的觀測值出現極值時，另一變量也出現極值的概率［5］.在前人的研究基礎上，由Copula函數的定義和性質，可以推算出尾部相關系數與Copula函數的關系表達式：

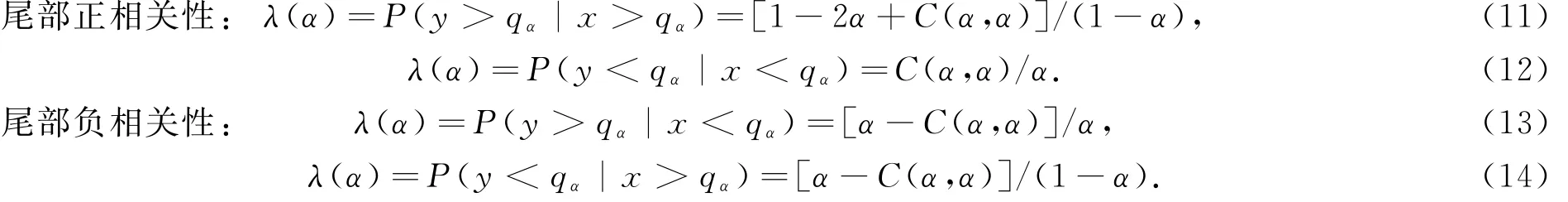
其中：α為概率；qα為相應的α的分位數.

用尾部相關系數λ分析金融市場間的尾部相關性是很方便的，它能反映一支股票價格（或股市）的大變動是否會引起另一支股票價格（或其他股市）的大變動，這對于有效降低投資風險具有較好的參考價值.

3 基于Copula函數上證指數的季度相關性分析

3.1 數據處理

上證綜指是上海第1支反映市場整體走勢的旗艦型指數，也是中國資本市場影響力最大的指數，總體上反映了上海證券交易所上市股票價格的變動情況，是中國資本市場的象征.因此，本文選取上證指數作為研究對象，研究其收盤價在季度上的相關關系.

本文選取的樣本數據為1991-2015年上證綜指的季線收盤價，共100個數據.季線數據來自同花順，它表示收盤價的一個季度即三個月的平均線.

為了對上證指數各季度收盤價之間的相關性有一個較直觀的了解，本文繪制了不同季度的上證指數收盤價的散點圖（見圖1）；為了觀察數據是否服從正態分布，繪制了P-P圖（見圖2）.

由圖1可以看出，上證指數各季度收盤價之間大致呈線性關系.由圖2（a）可以看出，數據點不均勻分布在理論直線即對角線的兩側，實際分布與理論分布有差距.圖2（b）反映了按正態分布計算后的實際值與理論值的差的分布.數據點不均勻分布在Y=0這條直線的上下側，絕對差異大于0.05，故認為該數據不服從正態分布.從第二、三、四季度的正態P-P圖和趨勢P-P圖也可得到以上結論.

由此可得，如果根據正態分布的假定來計算，就會產生不正確的估計結果.故本文將分別估計這些樣本數據的Pearson相關系數ρ1、Spearman相關系數ρ2和Kendall相關系數τ，多角度確定上證指數各季度的收盤價之間的相關性.

3.2 相關系數

利用SPSS19.0統計軟件，對1991-2015年各年各季度的收盤價進行相關性分析，相關系數的顯著性檢驗采用雙側檢驗.從表1可以看出，在置信度為0.01時，不同季度上證指數的收盤價的相關系數都在0.7以上，說明上證綜指各季度的收盤價之間表現出極強的正相關性.

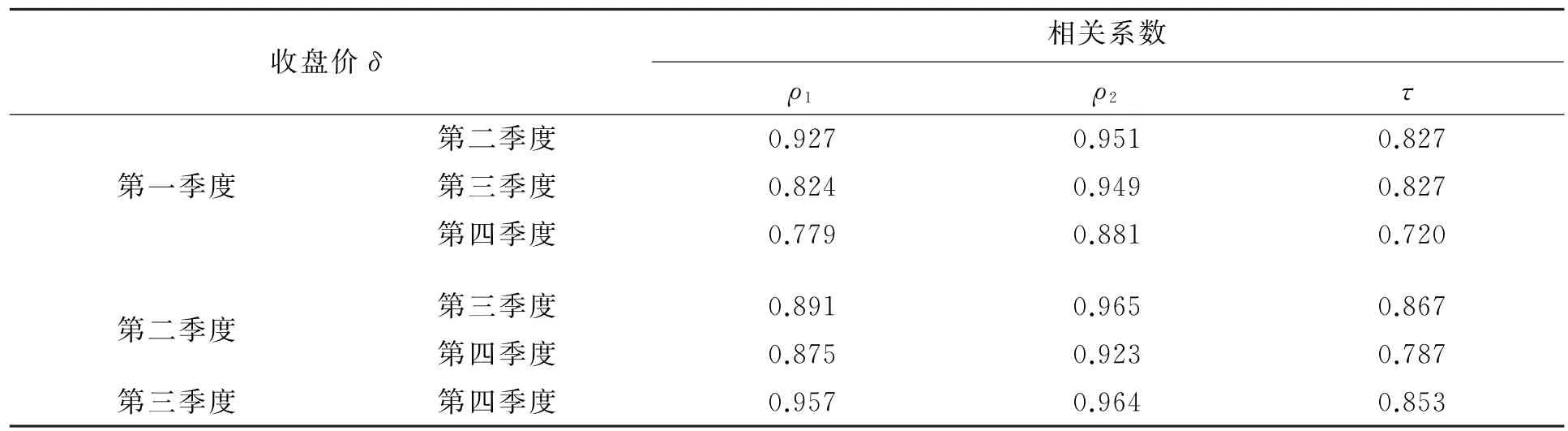
表1 上證指數各季度收盤價之間的相關性Table 1 The correlation between the closing price of Shanghai Composite index in the quarter

3.3 函數選擇

3.3.1 參數θ和理論的Copula函數

對于每個Copula函數，統計量τ都是θ的解析函數.采用估計阿基米德Copula參數的方法，將表1中的τ的各值代入相應的函數關系式（（2）式、（4）式、（6）式、（8）式），可估計出參數θ的值（見表2）.再將θ的值分別代入各函數表達式（（1）式、（3）式、（5）式、（7）式），可得到各函數在關于每兩個季度收盤價的表達式.

表2 參數θTable 2 The parameterθ

3.3.2 最優的Copula函數

本文選擇與經驗的Copula函數［5］誤差最小的理論的Copula函數作為最優的Copula函數.（10）式中各季度的樣本容量為n=25，為一固定值，所以次方即將大括號中的計算結果開方，也不影響結果的大小比較.因此，只要計算亦為固定值，不影響計算結果.大括號的

的值就可比較4個Copula函數與經驗的Copula函數之間的平均誤差，由此選擇誤差最小的函數作為最優函數.

采用C-free4編寫程序計算理論Copula函數與經驗Copula函數之間的誤差（C*）'，再將計算得到的誤差值分別代入（10）式可得誤差表3.結果表明，FGM函數與經驗Copula函數平均誤差最小，根據誤差最小原則，選擇FGM函數為最優函數.

表3 各理論的Copula函數與經驗Copula函數的誤差________________Table 3 The error between theoretical Copula function and empirical Copula function

3.4 尾部相關性

本文考慮了當α=0.925、α=0.975、α=0.995時的上尾部相關性，以及當α=0.010、α=0.050、α=0.100時的下尾部相關性.通過C-free4編寫程序，利用（11）式～（14）式計算FGM函數下的尾部相關系數（見表4）.由于通過負尾部相關表達式得到的相關系數值存在負數，不具實際意義，因此可判斷各季度收盤價之間不存在負尾部相關性.

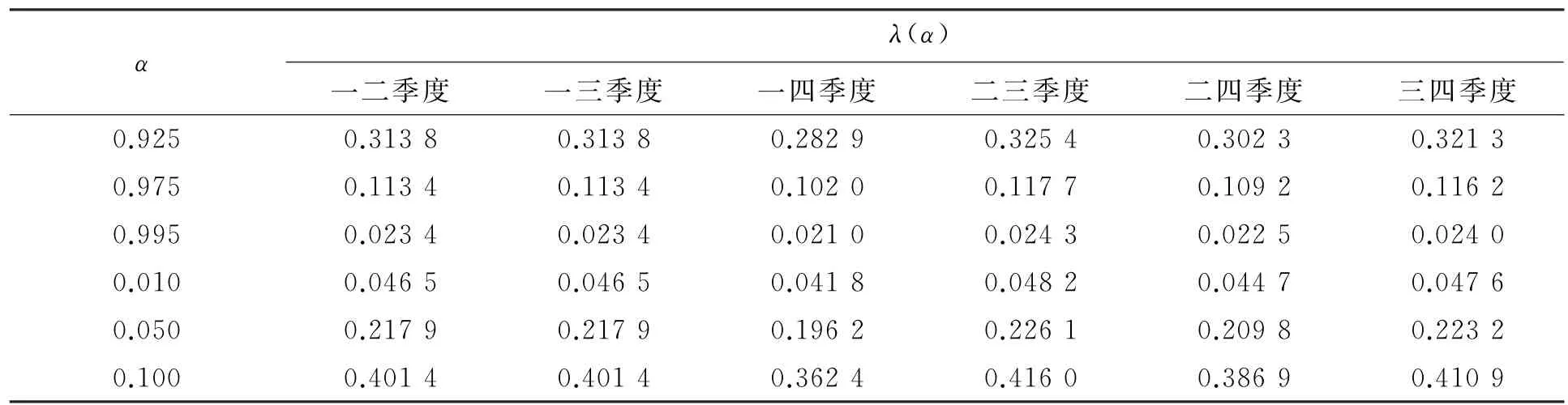
表4 FGM函數下的尾部相關系數Tabe4 Tail correlation coefficient of FGM

以一二季度為例，當第一季度的上證指數收盤價超過q0.925、q0.975、q0.995時，第二季度的上證指數收盤價超過相應分位數的概率分別是0.313 8、0.113 4、0.023 4，分別大于0.075、0.025、0.005，說明第一季度的上證指數和第二季度的上證指數存在著正尾部相關性.即：當α=0.925時，根據一二季度的上證指數的尾部相關性，可以說當第一季度的上證指數超過q0.925時，第二季度的上證指數超過q0.925的概率為31.38%.經分析，其他每兩季度之間也呈現出明顯的正尾部相關性.

4 結論

本文基于Copula函數在尾部相關性研究的應用理論，建立了Copula函數模型，對不同季度上證指數的尾部相關性進行研究.通過上證指數進行實證分析，可知各季度收盤價間有正尾部相關性.尾部相關性研究量化了投資風險，使投資者或風險管理預測者可依據季度間的股價指數尾部相關性預測股指在一個季度發生變化時，下一季度或另一季度發生變化的概率，這對于規避投資風險尤為重要.

［1］王軍.基于Copula方法的中國股票市場的相關性研究［D］.長沙：湖南大學，2010.

［2］劉國光，許世剛.基于Copula方法深圳A股、B股投資組合風險值實證分析［J］.淮海工學院學報（自然科學版），2004，13（4）：82-84.

［3］邱樹萍，吳薇薇，侯美麗.基于Copula函數的航班延誤相關性分析［J］.武漢理工大學學報（交通科學與工程版），2015，39（1）：117-120.

［4］吳高鍵，錢凱，伍笑萍.基于Copula理論的黃金和石油投資組合風險研究［J］.2015，36（9）：8-11.

［5］司繼文，蒙堅玲，龔樸.國內外股票市場相關性的Copula分析［J］.華中科技大學學報（自然科學版）.2005，33（1）：144-166.

［6］NELSEN R B.An introduction to Copulas［M］.New York：Springer，1998.

［7］史道濟，李璠.基于Copula的股票市場VaR和最優投資組合分析［J］.天津理工大學學報，2007，23（3）：13-16.

［8］HURLIMANN W.Fitting bivariate cumulative returns with copulas［J］.Computational Statistics&Data Analysis，2004（45）：355-372.

Quarterly Correlation Analysis of Shanghai Composite Index Based on Copula Function

JIANG Yingying，LIU Wenqiong
（School of Science，Huzhou University，Huzhou 313000，China）

The paper studied the tail dependence of the Shanghai Composite Index in different quarters with the theory of tail dependence based on Copula function.According to the empirical study based on Shanghai Composite Index，the results showed that it had positive tail correlation between the closing prices in each quarter.And the study of tail dependence provides a new way for the quantitative management of risk.

Copula function；optimal function；tail dependence；Shanghai Composite Index

F830.9

A

1009-1734（2016）04-0018-06

［責任編輯 高俊娥］

2016-03-02

劉文瓊，講師，博士，研究方向：信用風險管理、數據處理.E-mail：wenqiong6510@126.com

MSC 2010：91G70