模擬離子在緩沖氣體中運(yùn)動(dòng)的硬球碰撞模型

高瑛俏，沈夢(mèng)佳，孫宇梁

（湖州師范學(xué)院理學(xué)院，浙江湖州313000）

模擬離子在緩沖氣體中運(yùn)動(dòng)的硬球碰撞模型

高瑛俏，沈夢(mèng)佳，孫宇梁

（湖州師范學(xué)院理學(xué)院，浙江湖州313000）

為了研究RFQ冷卻聚束器、彭寧阱等核物理實(shí)驗(yàn)設(shè)備中離子的運(yùn)動(dòng)情況，從大學(xué)物理課本中的理想氣體的微觀模型出發(fā)，建立了用于模擬離子在氣體分子中運(yùn)動(dòng)的硬球碰撞模型.該模型通過(guò)計(jì)算離子在運(yùn)動(dòng)過(guò)程中與氣體分子的碰撞概率、碰撞后的運(yùn)動(dòng)速度，以及大量次數(shù)的模擬來(lái)研究離子在氣體中的運(yùn)動(dòng)情況.通過(guò)比較模擬結(jié)果和實(shí)驗(yàn)數(shù)據(jù)，得出模型適用于離子能量較低（低于約5 e V/u）的情況，這是因?yàn)槟Ｐ椭须x子與氣體分子的作用僅被當(dāng)作彈性碰撞來(lái)處理.RFQ冷卻聚束器、彭寧阱等核物理實(shí)驗(yàn)設(shè)備中離子的入射能量在模型的適用范圍內(nèi)，因此使用硬球碰撞模型并考慮設(shè)備所產(chǎn)生的電磁場(chǎng)對(duì)離子的作用，可研究離子在這些設(shè)備中的運(yùn)動(dòng)情況.

離子；緩沖氣體；硬球碰撞；適用范圍

在核物理研究領(lǐng)域，一些實(shí)驗(yàn)設(shè)備在運(yùn)行時(shí)需要對(duì)離子進(jìn)行冷卻.由于緩沖氣體具有將離子冷卻至其熱力學(xué)溫度的特性，而且實(shí)現(xiàn)方法相對(duì)簡(jiǎn)單，因此緩沖氣體冷卻是諸多實(shí)驗(yàn)設(shè)備最常采用的冷卻方法.例如，在緩沖氣體和四極交變電場(chǎng)的共同作用下，RFQ冷卻聚束器可實(shí)現(xiàn)降低束流能量、能散和發(fā)射度的效果［1-4］，用于原子核質(zhì)量精確測(cè)量的彭寧離子阱也是通過(guò)緩沖氣體和激發(fā)場(chǎng)的作用改變離子的運(yùn)動(dòng)狀態(tài)［5］.在研制這些實(shí)驗(yàn)設(shè)備之前，需對(duì)設(shè)備運(yùn)行的整個(gè)過(guò)程進(jìn)行模擬，通過(guò)在模擬過(guò)程中不斷調(diào)試確定出運(yùn)行時(shí)所需設(shè)定的各項(xiàng)參數(shù)［6］.為了在模擬過(guò)程中體現(xiàn)緩沖氣體對(duì)離子的作用效果，需要建立離子在緩沖氣體中的運(yùn)動(dòng)模型.

在《大學(xué)物理》課程的《氣體動(dòng)理論》這一章內(nèi)容里，為了求得理想氣體的壓強(qiáng)公式以及與大量分子運(yùn)動(dòng)有關(guān)的一些物理量的平均值（如平均能量、平均速度、平均碰撞次數(shù)等），建立了一個(gè)理想氣體的微觀模型，該模型提出以下幾點(diǎn)假設(shè)［7］：①把分子視為質(zhì)點(diǎn)；②忽略了分子間的長(zhǎng)程力；③分子的動(dòng)能較低時(shí)，把分子間的碰撞均視為完全彈性碰撞；④分子的運(yùn)動(dòng)遵從經(jīng)典力學(xué)的規(guī)律.在此微觀模型的基礎(chǔ)上，可以建立一個(gè)理論模型，模擬離子在氣體中運(yùn)動(dòng)的過(guò)程.因?yàn)槟Ｐ椭须x子與氣體分子的碰撞均被視為完全彈性碰撞，所以把該模型稱(chēng)為硬球碰撞模型.

1 建立模型

用硬球碰撞模型對(duì)離子在氣體中的運(yùn)動(dòng)進(jìn)行模擬時(shí)，需執(zhí)行一定數(shù)目的時(shí)間間隔.在每一個(gè)時(shí)間間隔中，進(jìn)行圖1中所示的幾個(gè)步驟：計(jì)算發(fā)生碰撞的概率、判斷是否發(fā)生碰撞、離子做勻速直線(xiàn)運(yùn)動(dòng)直至下一時(shí)間間隔（若發(fā)生碰撞需計(jì)算碰撞后離子的速度，碰撞不發(fā)生則保留之前的速度）.每個(gè)時(shí)間間隔的時(shí)長(zhǎng)被稱(chēng)為時(shí)間步長(zhǎng)（d t），d t越小，模擬的精度越高，當(dāng)然計(jì)算量也越大.這里分別對(duì)幾個(gè)步驟進(jìn)行介紹.

Fig. 1 The flow chart of the hard-sphere collision model

1.1 計(jì)算碰撞概率和判斷碰撞是否發(fā)生

課本已推導(dǎo)得到，分子平均碰撞次數(shù)（單位時(shí)間內(nèi)一個(gè)氣體分子和其它氣體分子碰撞的平均次數(shù)）為：［7］

其中：d為氣體分子的有效直徑；u-為某一氣體分子相對(duì)其他分子運(yùn)動(dòng)的平均速率；n為氣體分子數(shù)密度.若換成是離子在氣體中的運(yùn)動(dòng)，它的平均碰撞次數(shù)應(yīng)當(dāng)為：

其中：rion、rgas為離子、氣體分子的范德瓦爾斯半徑；c為離子相對(duì)氣體分子運(yùn)動(dòng)的平均速率.因?yàn)闅怏w分子的速率呈Maxwell分布，所以c值要由積分求平均得到：

令在一個(gè)時(shí)間步長(zhǎng)的時(shí)間里離子發(fā)生碰撞的概率為f.因?yàn)樵谝粋€(gè)時(shí)間步長(zhǎng)里，做勻速直線(xiàn)運(yùn)動(dòng)的離子移動(dòng)距離為：

而離子在移動(dòng)距離d x后，碰撞概率的增加量d f與1-f的比值，應(yīng)等于d x與平均自由程的比值：

從而得到發(fā)生碰撞的概率為：

模擬時(shí)用rand（）函數(shù)產(chǎn)生0～1的隨機(jī)數(shù)，當(dāng)隨機(jī)數(shù)小于f時(shí)碰撞發(fā)生.

1.2 計(jì)算碰撞后離子的速度

離子入射到氣體中后，與離子發(fā)生碰撞的氣體分子的運(yùn)動(dòng)速度不僅是服從Maxwell分布，而且其分布概率還與離子相對(duì)氣體分子的速度v'ion=vion-vgas成正比，即成正比，即

因此，可用這樣的方法產(chǎn)生與離子發(fā)生碰撞的氣體分子的速度：先按Maxwell分布產(chǎn)生一個(gè)速度vgas，再?zèng)Q定是否采納這個(gè)速度，采納這個(gè)速度的概率與vion-vgas的大小成正比.

引入?yún)?shù)R表示離子與氣體分子的碰撞程度，R等于x（如圖2所示，即離子與氣體分子的質(zhì)心距離在v'ion的垂直方向上的投影）與離子、氣體分子半徑之和的比值.R的取值范圍為［0，1），0表示離子與氣體分子對(duì)心碰撞，1表示兩者擦邊而過(guò).R的概率密度f(wàn)（R）是與2πR d R（即半徑為R的圓環(huán)面積）成正比的，乘以歸一化常數(shù)后得f（R）=2R，知道概率后即可通過(guò)產(chǎn)生隨機(jī)數(shù)來(lái)產(chǎn)生R的值：

因?yàn)镽=1時(shí)離子與氣體分子擦邊而過(guò)碰撞不發(fā)生，所以為了不讓R等于1，在式（9）中乘以0.999 9.令θ為碰撞時(shí)v'ion方向與離子原子質(zhì)心連線(xiàn)的夾角，有：

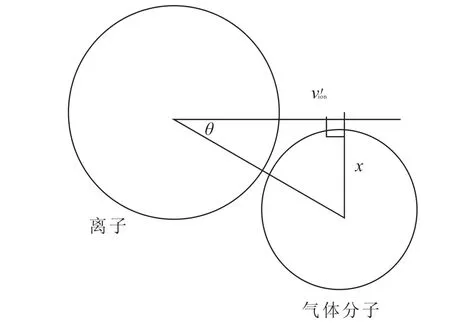
Fig. 2 The geometrical illustration of ion and gas molecule's collision

但僅有θ還不能完全確定碰撞時(shí)離子的運(yùn)動(dòng)方向，因此用隨機(jī)函數(shù)產(chǎn)生另一個(gè)方向角：

離子相對(duì)氣體分子的運(yùn)動(dòng)速度為v'ion在質(zhì)心連線(xiàn)方向上的分量為vr=v'ioncosθ，在垂直質(zhì)心連線(xiàn)方向上的速度分量為vt=v'ionsinθ.由動(dòng)量守恒和能量守恒可得：

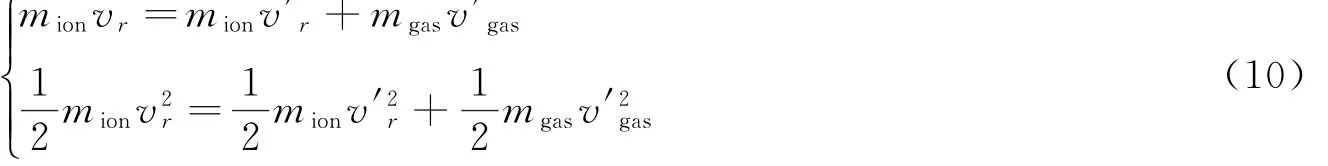
解得碰撞后離子相對(duì)氣體分子的運(yùn)動(dòng)速度在質(zhì)心連線(xiàn)方向上的分量為：

由兩個(gè)方向角θ和φ就可以推得碰撞后離子各個(gè)方向的速度分量.

1.3 進(jìn)行大量的模擬求平均值

大量分子作熱運(yùn)動(dòng)時(shí)具有一種有別于力學(xué)規(guī)律性的統(tǒng)計(jì)規(guī)律性，因此可以用統(tǒng)計(jì)的方法求出與大量分子運(yùn)動(dòng)有關(guān)的一些物理量的平均值，即進(jìn)行大量的模擬，把得到的數(shù)據(jù)求平均值，進(jìn)而從模擬結(jié)果中得出結(jié)論.建立好理論模型后，需要編輯程序在計(jì)算機(jī)上運(yùn)行，SIMION 8.0是用來(lái)模擬離子運(yùn)動(dòng)的專(zhuān)業(yè)軟件，運(yùn)行時(shí)可畫(huà)出離子的運(yùn)動(dòng)軌跡［8］.此外，用Mathematica、C++、Forture等軟件也可以編程進(jìn)行模擬.

2 確定模型適用范圍

模型建立后，為了確定模型的適用范圍，需把模擬得到的結(jié)果與實(shí)驗(yàn)測(cè)量的結(jié)果進(jìn)行比較，這些比較量可以是離子的射程、能損、偏轉(zhuǎn)角度等.射程為離子從入射到最終停止在氣體中所經(jīng)過(guò)的路程，但由于氣體分子的熱運(yùn)動(dòng)以及離子與氣體分子的不斷碰撞，離子不可能完全靜止下來(lái)，因此取離子從入射到達(dá)到熱運(yùn)動(dòng)速度時(shí)所經(jīng)過(guò)的路程為射程.由于目的是確定模型適用的離子能量區(qū)間，而不對(duì)氣體壓強(qiáng)（或密度）進(jìn)行專(zhuān)門(mén)的考慮，定義阻止距離（Stopping range）這一概念，它等于射程乘以氣體密度，這樣就消除了氣體壓強(qiáng)（或密度）的因素.RFQ冷卻聚束器、彭寧阱等設(shè)備通常用氦氣作為緩沖氣體［1-5］，因此選取氦氣作為模擬的氣體對(duì)象，另選擇40Ar+、133Cs+、201Hg+分別代表較輕質(zhì)量、中等質(zhì)量和很重質(zhì)量的三種離子.圖3是模擬結(jié)果與實(shí)驗(yàn)數(shù)據(jù)的比較，橫坐標(biāo)是離子的每核子入射能量，縱坐標(biāo)為阻止距離，模擬得到的數(shù)據(jù)點(diǎn)的誤差來(lái)源于數(shù)據(jù)的統(tǒng)計(jì)誤差.由SRIM軟件［9］計(jì)算得到的數(shù)據(jù)被作為“實(shí)驗(yàn)數(shù)據(jù)”使用（Paul and Schinner把收集到的大量實(shí)驗(yàn)數(shù)據(jù)與SRIM計(jì)算結(jié)果進(jìn)行比較，發(fā)現(xiàn)對(duì)于所有不同種類(lèi)的離子、在不同的能量區(qū)域，SRIM計(jì)算結(jié)果與實(shí)驗(yàn)數(shù)據(jù)都符合的很好［10］）.從圖3中可以看出，在離子能量低于約5 eV/u的時(shí)候，硬球碰撞模型模擬得到阻止距離與SRIM的數(shù)據(jù)符合得比較好，也就是說(shuō)，硬球碰撞模型可以用于模擬能量小于5 eV/u的離子在He氣中的運(yùn)動(dòng).模型不適用于更高的能量范圍是由于當(dāng)能量更高時(shí)，離子與氣體分子的作用不僅僅是簡(jiǎn)單的彈性碰撞，還存在其它的相互作用，如分子間的長(zhǎng)程相互作用、離子對(duì)氣體分子的電離和激發(fā)作用、離子與氣體分子的原子核間的庫(kù)倫作用和碰撞（彈性和非彈性）等.因此，若想將模型的適用范圍擴(kuò)展到更高的能量范圍，需在模型中添加這些相互作用.RFQ冷卻聚束器、彭寧阱等核物理實(shí)驗(yàn)設(shè)備中離子的入射能量在模型適用的能量范圍內(nèi)［1-5］，因此使用該模型并考慮設(shè)備所產(chǎn)生的電磁場(chǎng)對(duì)離子的作用后，可研究離子在這些設(shè)備中的運(yùn)動(dòng)情況.

Fig. 3 The stopping ranges of three ions in He- gas as a function of ion's energy per nucleon

射程（R）是較容易通過(guò)模擬得到的數(shù)據(jù)量，但通過(guò)比較射程來(lái)確定模型適用范圍易產(chǎn)生誤差.這是因?yàn)椋玫诫x子的射程，需要模擬離子由初始能量降到熱運(yùn)動(dòng)能量的整個(gè)過(guò)程，若某種模型在低能范圍是不適用的，則可能對(duì)從整個(gè)過(guò)程模擬得到的射程值產(chǎn)生影響.比如說(shuō)，模型在能量E 2附近是不適用的，對(duì)于離子從能量E 1（E 1＜E 2）降到熱運(yùn)動(dòng)能量所走過(guò)的路程（射程），實(shí)際值和模擬得到的值分別為x1，x'1（x1≠x'1）；對(duì)于離子從能量E 2降到能量E 1所走過(guò)的路程（射程），實(shí)際值和模擬得到的值分別為x2，x'2（x2≠x'2），可能出現(xiàn)x1+x2≈x'1+x'2的情況，從而得出在能量E 2附近模型是適用的錯(cuò)誤結(jié)論.若想更精確的確定出模型的適用范圍，可通過(guò)比較E-d E/d x曲線(xiàn)來(lái)確定范圍.但d E/d x（離子行進(jìn)單位距離所損失的能量）這個(gè)數(shù)據(jù)不能直接通過(guò)模擬得到，為了得到d E/d x，需先根據(jù)射程數(shù)據(jù)擬合得到函數(shù)E（R），再把E（R）對(duì)R求導(dǎo)，得到d E/d x（R）.

3 離子間的庫(kù)倫相互作用

在進(jìn)行核物理實(shí)驗(yàn)時(shí)，從重離子加速器進(jìn)入到RFQ冷卻聚束器中的離子數(shù)目較多，在用于去除雜質(zhì)離子的純化彭寧阱中的離子數(shù)目也不只一個(gè)，對(duì)于這些情況，離子之間的庫(kù)倫力是需要考慮的.因此，在模型中加入離子之間庫(kù)倫力效應(yīng)，模擬結(jié)果將會(huì)更符合實(shí)際情況.

為了在模型中添加入離子之間庫(kù)倫力的效應(yīng)，在程序每運(yùn)行一個(gè)時(shí)間步長(zhǎng)后，讀出每個(gè)離子的位置，根據(jù)離子的位置計(jì)算出該時(shí)刻其余離子對(duì)所研究離子的總的庫(kù)侖力作用，在下一個(gè)時(shí)間步長(zhǎng)里，認(rèn)為該庫(kù)倫力是不變的，直到下一個(gè)時(shí)間步長(zhǎng)結(jié)束，再重新確定所有離子位置后再算出新的庫(kù)侖力，如此循環(huán).該方法所考慮的庫(kù)倫力效應(yīng)比較符合實(shí)際情況，其誤差由時(shí)間步長(zhǎng)的大小決定.

4 總結(jié)

從大學(xué)物理課本中理想氣體的微觀模型出發(fā)，建立了模擬離子在氣體分子中運(yùn)動(dòng)的硬球碰撞模型.該模型通過(guò)計(jì)算離子在運(yùn)動(dòng)過(guò)程中與氣體分子的碰撞概率、碰撞后的運(yùn)動(dòng)速度，以及大量的重復(fù)模擬來(lái)研究離子在氣體中的運(yùn)動(dòng)情況.由于只把離子與氣體分子的作用當(dāng)做彈性碰撞來(lái)處理，因此該模型僅適用于入射離子能量較低（低于5 eV/u）的情況.RFQ冷卻聚束器、彭寧阱等核物理實(shí)驗(yàn)設(shè)備中離子的入射能量在該范圍內(nèi)，因此使用硬球碰撞模型并考慮設(shè)備所產(chǎn)生的電磁場(chǎng)對(duì)離子的作用后，可研究離子在這些設(shè)備中的運(yùn)動(dòng)情況.若想將模型的適用范圍擴(kuò)展到更高的能量范圍，需在模型中添加電離、激發(fā)、長(zhǎng)程等相互作用.

［1］NIEMINEN A，HUIKARI J，JOKINEN A，et al.Beam cooler for low-energy radioactive ions［J］.Nucl Instrum Methods A，2001，469：244.

［2］HERFURTH F，DILLING J，KELLERBAUER A，et al.A linear radiofrequency ion trap for accumulation，bunching，and emittance improvement of radioactive ion beams［J］.Nucl Instrum Methods A，2001，469：254.

［3］SAVARD G，CLARK J，BOUDREAU C，et al.Development and operation of gas catchers to thermalize fusion-evaporation and fragmentation products［J］.Nucl Instrum Methods B，2003，204：582.

［4］SCHWARZ S，BOLLEN G，LAWTON D，et al.A second-generation ion beam buncher and cooler［J］.Nucl Instrum Methods B，2003，204：474.

［5］SUN Y L，TIAN Y L，HUANG W X，et al.Numerical and graphical description on the ion motions in a Penning trap for mass measurement［J］.Nucl Instrum Methods A，2013，724：83.

［6］SCHWARZ S.IonCool-A versatile code to characterize gas-filled ion bunchers and coolers（not only）for nuclear physics applications［J］.Nucl Instrum Methods A，2006，566：233.

［7］馬文蔚.物理學(xué)教程上冊(cè)（第二版）［M］.北京：高等教育出版社，2006：186，199.

［8］MANURA D J，DAHL D A.SIMION 8.0 User Manual［M］.Idaho：Scientific Instrument Services Inc.，Idaho National Laboratory，2006.

［9］ZIEGLER J F，ZIEGLER M D，BIERSACK J P.SRIM-The stopping and range of ions in matter［J］.Nucl Instrum Methods B，2010，268：1 818.

［10］PAUL H，SCHINNER A.Judging the reliability of stopping power tables and programs for heavy ions［J］.Nucl Instrum Methods B，2003，209：252.

On the Hard-Sphere Collision Model Used to Simulate the Ion's Motion in Buffer Gas

GAO YINGqiao，SHEN Mengjia，SUN Yuliang（School of Science，Huzhou University，Huzhou 313000，China）

In order to study the ion's motion in Radio frequency quadrupole（RFQ）cooler and buncher and Penning trap，a hard-sphere collision model was built base on the ideal gas's microscopic model. The model can be used to simulate and study the ion's motion in gas by calculating the probability of collision，velocity after the collision and a large number of simulations.By comparing the simulated data with experimental data，it found that the model should be used when the ion's energy is less than 5 eV/ u，because the effect of ion and gas was treated as elastic collision.The energy of ions in RFQ cooler and buncher and Penning trap is in range of the model's application，so the model can be used to study the ion's motion in these equipments after considering the effect of the electromagnetic field produced by equipment.

ion；buffer gas；hard-sphere collision；range of application

O571.6

A

1009-1734（2016）04-0035-05

［責(zé)任編輯 邵圣文］

2016-03-12

國(guó)家自然科學(xué)基金（11405054）；湖州師范學(xué)院“大學(xué)生創(chuàng)新創(chuàng)業(yè)訓(xùn)練計(jì)劃”（2015-124）.

孫宇梁，講師，博士，研究方向：原子核物理.E-mail：sunyl@hutc.zj.cn